Лекция. Дріс 2 Затты рылысы. Заттарды агрегатты кйлері. Газ задары. Заттарды агрегатты кйлеріні сипаттамасы

• Название: Дріс 2 Затты рылысы. Заттарды агрегатты кйлері. Газ задары. Заттарды агрегатты кйлеріні сипаттамасы
• Анкор: Лекция
• Дата: 16.12.2022
• Размер: 157.67 Kb.
• Имя файла: Лек 2 Ñ„ÐºÑ .docx
• Тип: Документы; #847971

Дәріс №2

Заттың құрылысы. Заттардың агрегаттық күйлері. Газ заңдары.
Заттардың агрегаттық күйлерінің сипаттамасы

Заттар сыртқы ортаға байланысты (температура және қысым) төрт түрлі: газ, сұйық, қатты және плазма агрегаттық күйде бола алады.

Физикалық және коллоидтық химия плазмалық күйді қарастырмайды, өйткені плазмалық күйде зат молекулалары температурасы 5000 °С жоғары зарядталған иондар және электрондар түзіп, диссоциацияланады. Бұл күйдегі заттардың электрөткізгіштігі және соған байланысты басқа да қасиеттері өзгеше болады.

Заттың бір агрегаттық күйден екінші күйге ауысуы агрегаттық

түрлену деп аталады. Көптеген заттар белгілі бір температура мен қысымда бірден үш күйде бола алады. Мысалы суды алып қарасақ, ол бу, сұйық және мұз күйінде болады. 1.1- суретте су күйінің диаграммасы көрсетілген. Диаграммадағы қисықтардан екі агрегаттық аймақтың шекарасын көреміз. ОА қисығы – мұз бетіндегі қаныққан будың өзгеруін, ОВ қисығы сұйық су бетіндегі қаныққан будың өзгеруін, ал ОС қисығы қысымға байланысты мұздың балқу (еру) температурасының өзгеруін көрсетеді. Диаграммадағы О нүктесі үштік нүкте деп аталады. Осы нүктеге сәйкес келетін жүйеде белгілі температура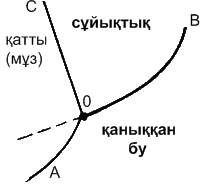

1.1-сурет. Су күйінің диаграммасы

да газ күйінде алуға болмайды.

Кейбір заттар тек бір, екі ғана күйге ұшырайды. Мысалы, нафталин, йод, күшәндер қатты күйден бірден буға айналады. Мәселен, кальций карбонаты сұйық күйінде де, газ күйінде де алынбайды. Өйткені ол қыздырғанда кальций оксиді мен көміртек (IV) оксидіне ыдырайды. Крахмал, белокты

Заттардың осы үш күйі – олардың айырмашылығы, молекулаларының өзара арақашықтығы мен әрекеттесу дәрежесіне байланысты болады. Газ күйіндегі заттардың атомдары мен молекулалары бір-бірінен өте алшақта болатындықтан, олардың молекулааралық күштері өте әлсіз. Газ күйіндегі заттар кез келген көлемде бола алады. Сондықтан, оларды жоғары қысыммен қыса отырып, сұйық немесе қатты күйге айналдыруға болады. Кейбір заттардың газ күйінде жеке молекула емес, екі, үш бөлшектен тұратын жиынтық түрінде де болуы мүмкін.

Сұйық күйіндегі заттар молекулаларының әрекеттесу күші (газдарға қарағанда) көбірек болады. Сондықтан, сұйықтық молекулалары бір-бірінен тәуелсіз қозғалу қабілетін жоғалтып, бірінен-бірі өте қашықтықта болмайды. Сұйық күйіндегі дене көлемі аз, тек өзінің пішінін ғана өзгертетін болады. Сұйықтықтардың осындай қасиеті техникада көтергіш, тежегіш қондырғыларда т.б. мақсаттар үшін жиі қолданылады.

Қатты денелерде атомдар, молекулалар немесе иондар арасы өте жақын және олардың тебілу күштері тартылу күштерімен шамалас болады. Осы атомдар (молекулар мен иондар) белгілі бір тәртіппен араласып кристалдық тор түзеді.

Заттардың бір агрегаттық күйден екінші бір агрегаттық күйге ауысуы жүйе энергиясының өзгеруімен жүреді. Мысалы, балқу, булану кездерінде жылу сіңіріліп, ал конденсациялану және кристалдану кездерінде жылу бөлініп шығатын болады. Қатты және сұйық жүйелерді заттардың конденсацияланған күйлері дейді. Зат

қ

атты күйден сұйық күйге ауысқанда, сұйық күйден газ күйіне ауысуына қарағанда, энергия аз жұмсалады. Ендеше балқу жылуы оның булану жылуынан әрқашанда аз болады.

2. ГАЗДАР

   1. 
      Газдардың заңдары
      

Газдар молекулаларының аралықтары тым алшақ орналасады да, тығыздығы мен тұтқырлығы және молекулааралық күштері өте аз болады. Егер газ өте сиретілсе, оның молекулааралық күші газ молекулаларының алатын көлемі сол газдың алып тұрған келемінің үлесіне де жетпейді. Газдың осылай шексіз сиретілген күйін идеал жағдай деп атайды. Идеал газ да газдардың заңдарына бағынады. Ол заңдарды тәжірибе нәтижесінде Бойль-Мариотт, Гей-Люссак- Шарль және Авогадро тұжырымдап берді. Енді осы заңдарды қарастырайық. Бойль-Мариотт заңы бойынша тұрақты температурада берілген газ мөлшерінің көлемі оның қысымына кері пропорционал болады. Егер берілген газдың Р₁және Р₂қысымындағы көлемдерін V₁және V₂деп белгілесек, онда:
Р₁V₁=Р₂V₂=К (1)
мұндағы К-тұрақты шама.
Берілген газ мөлшерінің көлемі мен қысымының көбейтіндісі берілген температурада тұрақты шама екені теңдеуден (1) айқын байқалады. Көлемнің қысымға байланысты тәуелділігін 1.2- суреттен көре аламыз. Бұл қисықтар идеал газдың изотермалары деп аталады.

Гей-Люссак пен Шарльдің заңы (1802 ж.) тұрақты қысымдағы идеал газдың көлемі мен температурасы арасындағы байланысты көрсетеді. Егер газды тұрақты қысымда қыздырса, онда температура бір градусқа артқан сайын газдың көлемі (V_t) бастапқы 0°С температурасындағы көлемінен (V₀)1 / 273,16-ға) (≈1/273-ке) көбейеді:
V_t = V₀ + V₀∙ ^t/273. немесе

V_t = V₀ ( 1 + t /273) = V₀Т/273 (2)
Мұндағы Т-Кельвин бойынша температура (Т = 273,16 + t°), ал t°- Цельсий бойынша температура. Берілген газ мөлшері үшін V₀ / 273 тұрақты шама, сол себепті теңдеуді (2) былайша жазуға болады
V_t =КТ (2а)

немесе

V ₁ /Т ₁= V ₂ /Т₂(2ә)
Бұдан газ көлемінің абсолюттік температураға тура пропорционал болатынын көреміз.

Тұрақты көлемде газдың қысымы температура бір градусқа көбейгенде 1/273-ке артатындықтан, мынадай теңдеу жазуға болады:
Р = Р₀(1 + t /273) = Р₀Т/273 (3)
Сонымен Гей-Люссак және Шарль заңын былай тұжырымдай аламыз: тұрақты қысымда температураны 1°-қа өзгертсе, берілген мөлшердегі газдың 0° С температурасындағы көлемі 1/273-ке өзгереді немесе тұрақты көлемде температураны 1°-қа өзгертсе, берілген мөлшердегі газдың 0°С температурасындағы қысымы 1/273-ке өзгереді.

1.2-сурет. Идеал газдың

изотермалары

1.3-сурет. Идеал газдың изобаралары

Газ көлемі тұрақты болса, қысым да, көлем де абсолюттік температураға тура пропорционал болады:
Р=КТ (За)

Р₁ / Т = Р₂ / Т₂=К (Зә)
Теңдеуді (2) 1.3-суреттегідей түзулер арқылы көрсететін болсақ, бұл қисықтардың әрқайсысы тұрақты қысымға сәйкес келеді. Бұл қисықтар идеал газдың изобаралары деп аталады. Газдардың үшінші заңын Авогадро ашқандықтан (1811 ж.) Авогадро заңы деп аталады. Оны былай тұжырымдауға болады: бірдей қысым мен бірдей температурадағы әр түрлі газдардың бірдей көлемдерінің молекулалар саны да бірдей болады. 1 моль газдың көлемі 0°С температура және 760 мм сынап бағанасындағы қысымда - 1,01325· 10⁵Н/_м², V₀=22,415 л, ал газ құрамындағы молекулалардың саны Авогадро тұрақтысы деп аталады. Авогадро заңы химияны дамытуда үлкен рөл атқарды. Сондай-ақ XVIII ғасырдың ортасында М. В. Ломоносов тұжырымдаған атом- молекулалық ілімді мойындау және атом мен молекуланың массаларының шамаларын есептеуде де Авогадро санының маңызы зор.

2. Идеал газдар, олардың физикалық күйінің теңдеуі

Газдарға арналған идеал жағдай жоғарыда (2.1) баяндалды. Идеал жағдайдағы газдарды идеал газдар деп атайды. Газдардың физикалық күйі үш шамамен: температура (Т), қысым (Р) және көлеммен (V) сипатталады, ал олардың арасындағы байланысты сол жоғарыда айтылған газдардың үш заңын біріктіріп табуға болады. 0°С температурадағы және Р₀ қысымдағы берілген газ көлемін V₀ деп белгілейік. Егер температура Т болса, онда газдың көлемі - V_t ал қысымы Р_t-ға дейін өзгереді. Газды бір күйден екінші күйге екі түрлі жолмен ауыстыруға болады. Ең алдымен температурасын тұрақты етіп (Т₀), қысымды Р₀-дан Р_t-ға дейін өзгертсек, газдың көлемі V₀ -ден V₁ -ге дейін өзгереді. Бойль- Мариотт заңы бойынша: Р₀ V₀ = Р₁ V₁.

Егер температураны Т₀-ден Т-ға дейін өзгертіп, қысым тұрақты және Р₁болса, газдың көлемі V₀-ден V₁-ге дейін езгереді.

Гей-Люссак заңы бойынша: V₀ / Т₀= V₁ / Т₁. Осы теңдіктің оң жағы мен сол жағын Р₁-ге көбейтсек:

Р₀ V₀ / Т₀= Р₁ V₁ / Т₁; Р₁ V₁ = Р₀ V₀

екенін ескерсек, онда:

Р₀V₀ / Т₀= Р₁ V₁ / /Т₁.

Бұдан газдың кез келген күйі былай өрнектеледі:

Р V /Т=r , РV=r∙Т (4)

Мұндағы r – газдың табиғаты мен мөлшеріне тәуелді тұрақты шама. Бұл теңдеуді (4) Б. Э. Клайпеpoн 1834 ж. қорытып шығарды. Кейінірек Д. И. Менделеев Клайперон теңдеуіндегі r-ді 1 моль газға сәйкес тұрақтысымен ауыстырды: r = п R мұндағы п - газ мольдерінің саны. Сонда:

Р V = пRТ (5)

Бұл теңдеуді (5) идeал газ күйінің mеңдеуі немесе Клайпeрон- Менделеев теңдеуі деп аталады. Теңдеудегі (5) R-газдың табиғаты мен мөлшеріне байланыссыз тұрақты шама. Ол газдың универсал тұрақтысы деп аталады. R-дің сандық мәні қысым мен көлемнің өлшем бірліктеріне байланысты болады. Егер қысым атмосферамен, ал көлем литрмен өлшенсе, онда:

R=рV /Т=1∙22,414 /273,16≈0,082 л. атм/град∙моль Егер қысым дин/см, ал көлем см³ болса, онда.

R=РV/Т=76∙13,6∙0,81∙22,414/273,16=8,313∙10⁷эрг/град∙моль; 1 калорияның 4,18∙10⁷ эрг екенін ескерсек:

R =8,313∙10⁷/4,18∙10⁷=1,987 (немесе ≈ 2) кал (град∙моль) РV/Т өрнегі жұмыстың өлшемімен өлшенеді.

Олай болса, R деп отырғанымыз тұрақты қысымда температураны бір градусқа арттырғандағы 1 моль идеал газдың ұлғаю жұмысы болып табылады, ол өлшемдердің халықаралық жүйесінде (СИ) джоуль бойынша өрнектеледі:

R=8,313∙10³ дж / (град- кмоль)
Менделеев-Клайперон теңдеуі газдарға байланысты әр түрлі есептеулерде (мысалы, газдың массасы немесе газдың көлемін қалыпты жағдайға келтіру) қолданылады.

Газдың массасын табу үшін теңдеудегі (5) п мынадай етіп жазылады:

п = m/М

мұнда т - газдың мөлшері, М-газдың бір мольінің массасы. Сонда РV = mRТ/М, бұдан:

М = тRТ/РV (6)

Теңдеу (6) бойынша берілген газдың массасын есептеп табуға болады. Алайда массасын анықтайтын зат газ күйіне ауысқанда диссоциацияланбауын (ыдырамауын) ескеру керек. Мысалы, фосфор (V) хлоридін қыздырғанда, ол фосфор (Ш) хлориді мен хлорға ыдырайды.

Сондықтан формула (6) бойынша фосфор (V) хлоридінің массасы анықталмайды.

Ал газдардың көлемін қалыпты жағдайға келтіруде мынадай формулалар пайдаланылады:

Р₀ V₀ / 273=Р₁V₁/Т₁

Бұдан V₀ = Р₁ V₁ ∙ 273/ Т₁Р₀(7)

Идеал газ күйінің теңдеуін тек жеке газ емес, газдардың қоспасына да қолдануға болады. Әрине ондағы газдар өзара әрекеттеспеуі керек.

Дальтонның заңы (1807) бойынша газдар қоспасының жалпы қысымы олардың әрқайсысының үлестік қысымдарының қосындысына тең:

Р= Р₁+ Р₂+Р₃+...+Р_i(8)

Мұндағы Р-газ қоспасының жалпы қысымы, ал Р₁; Р₂; Р₃ ;... Р_i– қоспадағы құрамдас бөліктердің үлестік қысымдары. Егер газ қоспасы әр түрлі құрамдас бөліктердің п₁,п₂,п₃... п_імолінен тұратын болса, онда молдердің жалпы саны (п) мынаған тең: п = п₁ + п₂ +п₃

+ п_і. Газ қоспасының жалпы көлемі V, ал температурасы Т болса, ол қоспадағы құрамдас бөліктердің үлестік қысымдарын былай жазуға болады:

Р₁= п₁ RТ/ V; Р₂= п₂ RТ/ V;... Р_i = п_іRТ/ V (8^а)

(8^а) өрнектерді (8) теңдеуге қойсақ:

Р=(п_і+п₂+п₃ + ... п_і) ∙RТ/V=п∙RТ/V (8^б)


(8^а) өрнектерінің бірін (8^б) теңдеуіне бөліп, газ қоспасының жалпы қысымы мен оның бір құрамдас бөлігінің (і) үлестік қысымдарының арасындағы қатынасты білуге болады:

Р_i=п_I /п∙Р немесе Р_i=N_I/Р, (9)

Мұндағы N_iгаз қоспасындағы берілген і құрамдас бөліктің мольдік үлесі.

Газдардың кинетикалық теориясы

Газ заңдарының негізі болған молекулалық-кинетикалық теория (ілім) ХVІІІ ғасырдың ортасында тұжырымдалды. Оның негізгі қағидалары мыналар:

1. 
   Кез келген газ бірдей шар тәрізді серпімді молекулалардан тұрады. Ол молекулалардың шамасы молекулааралық
   

қашықтықтан өте аз болғандықтан, оларды материалдық нүкте ретінде қарастыруға болады.

2. 
   Молекулалар үздіксіз ретсіз қозғалыста болады. Бір молекула әр түрлі уақытта әр түрлі жылдамдық көрсетіп, оның жылжу бағыты да өзгеріп отырады.
   
3. 
   Молекулалардың бір-біріне деген әсері өте әлсіз, оны ескермесе де болады, олар өзара қақтығысқанда ғана бір-біріне әсер етеді:
   
4. 
   Қақтығысқан молекулалардың жалпы энергиясы өзгермейді, өйткені ол серпімді шарлардың соқтығысу заңына бағынады.
   

Газдардың кинетикалық ілімінің негізгі теңдеуі газдар молекулаларының қозғалысын зерттеудің нәтижесінде қорытылды:


А
РV=1/3∙N ∙mū²(10)

Теңдеудегі (10) шамалар бізге бұрыннан белгілі. Ал ū - молекулалардың орташа квадраттық жылдамдығы. Ол әрбір молекулалар жылдамдықтарының квадраттарының орташа мәнінің түбіріне тең:

ū
Теңдеуден (10) идеал газ заңдарын қорытуға болады және бұл теңдеуден әр түрлі салдар шығады. Теңдеудегі (10) РV өрнегін оған тең RТ-ге ауыстырып және т ū ²/2 өрнегін оң жаққа шығарып жазсақ:

RТ=2 / 3N₀∙тū²/2 (12)
болады.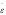

Теңдеудегі (12) т ū ²/2 өрнегін деп белгілейік, ол- молекулалардың ілгерілемелі қозғалысының орташа квадраттық энергиясы. Олай болса, теңдеуді (12) былай жазуға болады: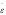

=³/₂∙R ∙T/N_А=³/₂∙RТ (13)

Мұндағы К=R/N₀, ол Больцман тұрақтысы деп аталады.

Больцман тұрақтысының сандық мәні мынаған тең:

К=R/N₀=8,314/6,02∙10²³=1,38∙10^-23 (джоуль/град) Теңдеу (13) газ молекулалары кинетикалық энергиясының абсолюттік энергияға тура пропорционал екенін көрсетеді. Олай болса, бірдей температурадағы газдардың орташа кинетикалық энергиясы бірдей болады.

Молекулалық-кинетикалық ілім бойынша абсолюттік нөл температурасы (Т₀) дегеніміз молекулалардың орташа кинетикалық энергиясының нөлге тең болатын температурасы болып шығады.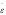

Егер газдың мөлшері 1 моль болса, онда оның кинетикалық энергиясы ∙N_Аболады. Оны Е деп белгілесек ∙N_А=Е

Е=³/₂∙RТ (14)

Молекулалардың қозғалу жылдамдықтары олардың массаларына, температураға байланысты.

Егер екі түрлі газдың бірдей температура және қысымдағы бірдей көлемін алып қарастырсақ, онда:

1 2 N
2


2
^m₁ ^u1
1/ 3N
2

^m₂ ^u2

немесе
2

^m₁ ^u1
2

^m₂ ^u 2

(15)

теңдеуден (15)

2 ^m2

/ m₁

немесе

u₁ / u₂

(16)

u
Сонымен екі түрлі газдың қозғалу жылдамдықтарының қатынасы олардың массалар қатынастарының түбіріне кері продорционал болады.

Тұрақты қысымда екі түрлі температура (Т₁және Т₂) үшін теңдеуді (10) былай жазуға болады:

2

^{Т1 үшін: 1 3 N mu}1
RT₁

(17)

Т₂үшін:
2

1. 
   ^{3 N m u}2
   

RT₂

(18)

теңдеуді (17) теңдеуге (18) бөліп жазсақ:

2 2

^u1 ^{/ u} 2

T₁ / T₂

немесе

u₁ / u₂

(19)

Теңдеуден (19) газдардың қозғалуының орташа жылдамдықтары абсолюттік температураның түбіріне тура пропорционал екенін көруге болады.

Теңдеуді (10) пайдаланып әр түрлі температурадағы газ молекулаларының орташа жылдамдығын есептеп, газдың молекулалық массасын табуға болады:

2

RT 1 3 mu

^немесе u

3RT / M

(20)

0°С температурасында молекулалардың орташа квадраттық жылдамдығы сутек үшін 1840, азот үшін 493, ал оттек үшін 461 м/сек болады. Бұдан газ молекулалары жылдамдықтарының үлкен шама екенін көреміз. Алайда газдардағы диффузияны зерттеу газдардың таралу жылдамдықтарының аз екенін көрсетті. Оның себебі газ молекулалары бір бағытта емес, бейберекет қозғалатын

болғандықтан олар өзара соқтығысып, өздерінің бастапқы жағдайынан онша қашықтамайды.

Молекулалар бейберекет қозғалатындықтан, ондағы жеке молекуланың жылдамдығы мен энергиясын табу мүмкін емес. Сондықтан молекулалардың орташа жылдамдығы, орташа энергиясы деген ұғымдар пайдаланылады. Соның нәтижесінде ықтималдылық теорияны қолданып, молекулалардың жылдамдығы мен энергиясы бойынша таралу заңдылықтарын қарастыруға мүмкіндік туады. Газдардың жылдамдықтары бойынша таралу заңын Д.К. Максвелл 1860 жылы ашқан болатын.

Мына кестедеде оттек молекулаларының қозғалу жылдамдықтары бойынша таралуы көрсетілген.
1.1-кесте 0°С температурасында оттек молекулаларының жылдамдықтары бойынша таралуы

жылдамдық шектері, м/с	берілген жылдамдықтары бар молекулалар үлесі, %	жылдамдық шектері, м/с	берілген жылдамдықтары бар молекулалар үлесі, %
100-ден кем	1,4	400 -ден 500-ге	20,3
100-200	8,1	500-600	15,1
200-300	16,7	600-700	9,2
300-400	21,5	700-800	7,7

Кесте мәліметтері бойынша барлық молекулалардың жартысына жуығы белгілі бір орташа жылдамдық (300 – 500 м/сек) көрсетеді екен.

Молекулалардың жылдамдық бойынша таралуы 1.4-суретте график түрінде көрсетілген. Ордината өсінде молекулалар саны (пайыздық түрде), ал абсцисса өсінде сол молекулалардың жылдамдықтары м/сек бойынша салынған.

Графиктен кез келген температурада молекулалардың белгілі бір бөлігінің ғана басқа молекулаларға қарағанда жоғарырақ белгілі бір жылдамдығы және кинетикалық энергиясы болатынын көреміз.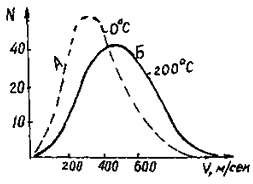


1.4-сурет. Молекулалардың жылдамдықтары бойынша таралуы

Графиктегі максимумге сәйкес келетін жылдамдық ықтималдылығы көп жылдамдық деп аталады. Берілген жағдайда ондай жылдамдықты молекулалар- дың көп бөлігінен көре аламыз. Оттек үшін ондай жылдамдық 0°С температура- сында 376 м/секқа тең. Температура артқан сайын максимум жылдамдықтың жоғары жағына (оңға қарай) ығысады және молекулалардың жылдамдық бойынша таралуы тек температураға байланысты екен. Сонымен Максвелл жасаған молекулалардың жылдамдық бойынша таралу заңын былайша тұжырымдауға болады: барлық молекулалар бірдей жылдамдықпен қозғалмайды, температура артқан сайын ықтималдылығы көп жылдамдық өседі.

Физикалық химияда Л. Больцман көрсеткен молекулалардың энергия бойынша таралу заңының да маңызы өте зор. Ол заң берілген молекулалар саны және олардың энергиясының арасындағы байланысты көрсетеді. Бұл заң бойынша тепе-теңдік жүйедегі энергиясы Е және одан көпмолекулалардың үлесі Больцман факторына тең:

N_ε/N=е^-ε/Ктнемесе М_ε=М∙е^-ε/Кт(21)

Мұндағы N_ε- энергиясы Е және одан да көп молекулалардың саны, N – молекулалардың жалпы саны, К-Больцман тұрақтысы.

Теңдеудің (21) алымын да, бөлімін де Авогадро санына көбейткенде:

М _ε=М ∙ е^-ε/RТ(22)

Мұндағы Е=NА∙ε – бір моль газдың кинетикалық энергиясы. R – ол газдың универсал тұрақтысы.

Реакция кезінде химиялық әрекеттесу кез келген соқтығысқан молекулалар емес, энергиясы Е-ге тең және одан да көп болатын молекулалар соқтығысқанда ғана жүреді. Ондай молекулаларды

активті (белсенді) молекулалар, ал теңдеудегі (22) Е-ні химиялық реакцияның активтену энергиясы деп атайды.

Реал газдар

Әр түрлі газдарды тәжірибе арқылы зерттеулерден алынған мәліметтер идеал газдардың заңдарынан ауытқитынын көрсетті. Мысалы кез келген газ үшін Бойль-Мариотт заңы бойынша көлем мен қысымның көбейтіндісі берілген температурада тұрақты болуы керек. (РV = К). Алайда азот үшін Р = 1 атм болғанда, РV = 100 болса, Р = 430, 86 атм болғанда, Р = 125,96 болады екен, яғни көлем мен қысымның көбейтіндісі тұрақты емес екен. Реал газдардың (ауаның) Бойль-Мариотт заңынан ауытқуын Ломоносов та көрсеткен болатын. Тәжірибе жүзінде бұл мәселені Д. М. Менделеев пен А. В. Реньо да қарастырды.

Жоғарыда айтылған ауытқулар неғұрлым температура төмен болған жағдайларда, ал қысым артқан сайын ол соғұрлым күштірек болады. Реал газдардың идеал газдар заңынан ауытқулары екі түрлі себептермен болады: олар - реал газдарда молекулалардың арасында тартылу және тебілу күштері және реал газдар молекулаларының меншікті көлемі болатындықтан.

Молекулалардың өзара тартылуының нәтижесінде олардың арақашықтықтары азайып, газдың көлемі кемиді. Сол Ван-дер- Ваальс күшінің әсерінен болатын қысым ішкі қысым деп аталады. Ол тығыздықтың квадратына тура пропорционал болады, яғни: Р=аd², мұндағы а – берілген газ үшін тұрақты шама. Газдың тығыздығы оның меншікті көлеміне кері пропорционал: d=1/ υ; ендеше Р=а/ υ². Мұндағы υ– газдың меншікті көлемі. Сонымен, біз газдың реал күйінің теңдеуін былай жаза аламыз:

(Р+а/υ²)(V-в)=пRТ (23)

Бұл теңдеуді (23) Ван-дер-Ваалъс теңдеуі деп атайды, мұндағы в- молекуланың көлеміне байланысты тұрақты шама, ол молекуланың меншікті көлемінен шамамен алғанда төрт есе аз, оны қысылмайтын көлем деп атайды.

Төмендегі кестеде кейбір газдар үшін а мен в -ның мәндері берілген:

1.2-кесте. Кейбір газдар үшін а және в коэффициенттерінің мәндері

ГАЗ

а м3/моль

м3/моль

ГАЗ

а м3/моль

м3/моль

Не

25,5 ∙ 108

23,9 ∙10-6

О2

1390 ∙ 108

31,9 ∙ 10-6

Н2

248 ∙ 108

26,7 ∙10-6

CO2

3660 ∙ 108

42,8 ∙10-6

N2

1368 ∙ 108

38,6 ∙10-6

Cl2

6585 ∙ 108

56,210 ∙10-6

CO

1480 ∙ 108

39,6 ∙10-6

H2O

5521 ∙ 108

30,410 ∙10-6

Бұл кестеден а мен в-ның мәндері әр түрлі газдар үшін олардың полярлығы мен массаларына байланысты көбірек өзгеретіні байқалады.

Газдардың тығыздығы азайған сайын реал газ күйінің теңдеуі идеал газ күйінің теңдеуіне жуықтай түседі.

Егер қысымды жоғарылатып, температураны төмендетсе, газдар сұйық күйге көшеді. 1823 жылы М. Фарадей хлор, аммиак сияқты газдарды қысу және салқындату арқылы сұйықтыққа айналдырды. Алайда ол кейбір газдарды, атап айтқанда, сутек, оттек, көміртек (II) оксиді азот сияқты газдарды сұйылта алмады. Сондықтан ондай газдар (сұйықтыққа айналдырылмайтын болғандықтан), “тұрақты” газдар деп аталды. 1860 жылы Д. И. Менделеев, кейінірек 1869 жылы Т. Эндрьюс кез келген газдың шектік температурасы болатынын, одан кейін қандай бір үлкен қысым болса да оның сұйылмайтынын айтты. Ол температураны Д. И. Менделеев абсолюттік қайнау температурасы десе, Т. Эндрьюс кризистік (дағдарыстық) температура деп атады. Дағдарыстық температурадағы газдың сұйылтатын қысым дағдарыстық қысым, ал оған сәйкес көлем дағдарыстық көлем деп аталады.

Дағдарыстық температура, дағдарыстық қысым және оларға сәйкес дағдарыстық көлем жағдайларындағы газды-газдың дағдарыстық жағдайы деп атайды.

Кейбір газдардың дағдарыстық константалары 1.3-кестеде көрсетілген:

1.3-кесте

Зат	температура	қысым, н/м3	Көлем, л
H2	-239,9	12,97∙105 33,93∙105 50,35∙105 73,85∙105 0,056∙105 2,7∙105	0,064
N2	-127		0,090
О2	-118,8		0,078
СО2	-31,3		0,094
H2O	-374,2		0,056
Не	-267,9		0,057

1.5-суретте тұрақты температурадағы реал газдың көлемі мен қысымының өзара қисық реал байланысы көрсетілген. Бұл

байланысты көрсететін қисықтар реал газ күйінің изотермалары деп аталады.

0°С температурасы сәйкес келетін изотерма газды қысқан сайын өз көлемін азаятынын көрсетеді. Көлем мен қысымның мәндері а-ға жеткенде көлемді әрі азайту в нүктесіне дейін газдың қысымын өзгертпейді. Әрі қарай көлемнің аздап өзгеруінің өзі-ақ қысымды күрт арттырып жібереді. Басқа изотермада да осындай заңдылықтар байқалады, тек температура артқан сайын қысымның горизонтальдік бөлігінің ұзындығы қысқара береді, яғни ав→а'в'→а"в" деп, 31 ⁰С температурасында тек бір нүкте (К) болып, ал одан жоғары температураларда изотерманың горизонтальдік бөлігі болмайды. 1.5-суреттегі изотермалар С(ІV) оксидінің қысылу кезіндегі тәжірибелік мәліметтер бойынша салынған.

Осы зерттеулер а, а', а" нүктелеріне сәйкес келетін қысым мен көлeмде газдың конденсациясының басталатынын көрсетті.

Конденсациялау процесі кезінде көлем азаяды, ал көлемнің нүктелеріне сәйкес келетін сұйықтық қаныққан сұйықтық деп аталады.

1.5-суреттегі К нүктесін дағдарыстық нүкте деп атайды. Осы нүктеге сәйкес келетін қысым мен көлемнің де дағдарыстық қысым (Р_К) және дағдарыстық көлем (V_K) болатыны жоғарыда баяндалды. Газдардың(Р_К) және (V_К)-сын анықтаудың жанама жолдарының бірі Кальте мен Матиас ұсынған

1.5-сурет. Реал газ

теңдеуінің изотермасы

түзу сызықты диаметр ережесіне негізделген. Ол ереже бойынша

сұйықтық пен оның қаныққан буы бір-біріне байланысты болады: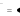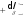

d d_c 2

a вm

(24)

Мұндағы d – орташа тығыздық: d _смен d_δсұйықтық пен оның қаныққан буының тығыздығы, а мен в -тұрақты шамалар.

Тәжірибе арқылы әр түрлі температурада d _смен d_δмәндерін анықтап алып d мен Т арасындағы тәуелділікті график түрінде салады. Температура артқан сайын сұйықтықтың тығыздығы кемиді де, оның буының тығыздығы артады, ал Т_к температурасында олар өзара теңеседі. Сұйықтық пен будың орташа тығыздығын сипаттайтын барлық нүктелер Т_ктемпературасына сәйкес келетін ОТ нүктесі арқылы өтетін түзудің (түзу сызықты диаметр) бойында жатады. Осы түзу сызықты диаметрдің ордината өсімен түзетін кесіндісі сандық тығыздыққа сәйкес келеді. Олай болса, дағдарыстық көлемді былайша табуға болады. υ_К=М/ d_к, Мұндағы М-газдың молекулалық массасы.

Дағдарыстық температураны білудің маңызы өте зор. Д. И. Менделеев кейбір газдардың сұйылмауының себебін оларды сұйылту кезіндегі тәжірибелерде газдардың абсолюттік қайнау температурасынан жоғары температурада жүргізілуінен деп түсіндірді. Егер тәжірибелер ол температурадан төменгі температураларда жүрсе, газдарды сұйылтуға болады деп көрсетті.

Шындығында кейінгі зерттеулер Менделеев пікірінің дұрыстығын дәлелдеді. Кейін оттек, азот, сутек сияқты «тұрақты газдар» да сұйық күйінде алынды.

1895 жылы ауаны сұйылтатын алғашқы қондырғы іске қосылды. Соңғы кездерде сұйылтылған газдар өндірісте кең қолданыла бастады. Сұйық оттек қопарғыш заттар алу үшін, авиация, металлургия т.б. өндірістерде, ал сұйық ауа лабораторияларда төменгі (-180°С-қа дейінгі) температуралар алу үшін қолданылады. Хлор, аммиак сияқты газдарды сұйық күйінде болаттан жасалған баллондарда сақтап тасымалдайды.