Барабаш тема 2. Ds как дугу окружности с радиусом M, будем иметь ds MdB
 Скачать 347.4 Kb.
|
|
Рассматривая элементарную дугу ds как дугу окружности с радиусом M, будем иметь: ds = MdB, или  .Длина дуги меридиана между точками, имеющими широты В1 и В2, выразится так:  . Таким образом, вычисление длины дуги меридиана сводится к нахождению эллиптического интеграла вида 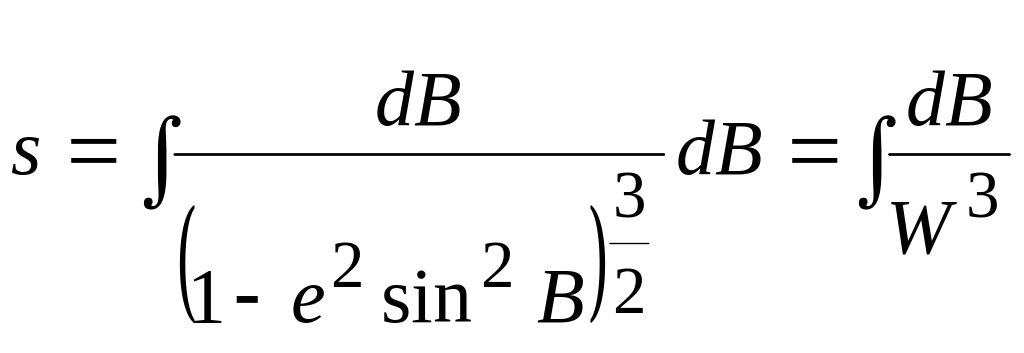 ,который, как известно, в элементарных функциях не интегрируется. Для вычисления указанного интеграла разложим подинтегральную функцию  в ряд по биному Ньютона, после чего почленно произведем интегрирование, удерживая необходимое число членов.Разложение дает:  Для простоты дальнейших выкладок ограничимся членами с е5. Четные степени синусов, входящих в разложение функции , в ряд, заменим косинусами четных дуг согласно следующим равенствам: 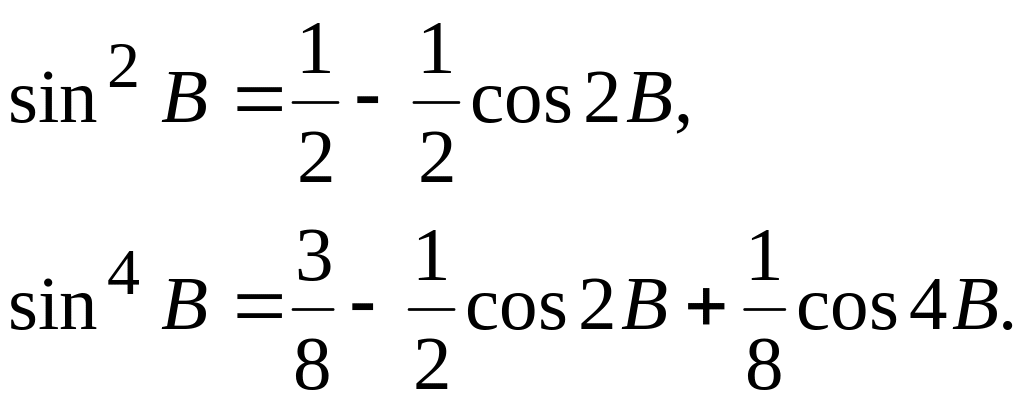 Теперь формула будет иметь вид: 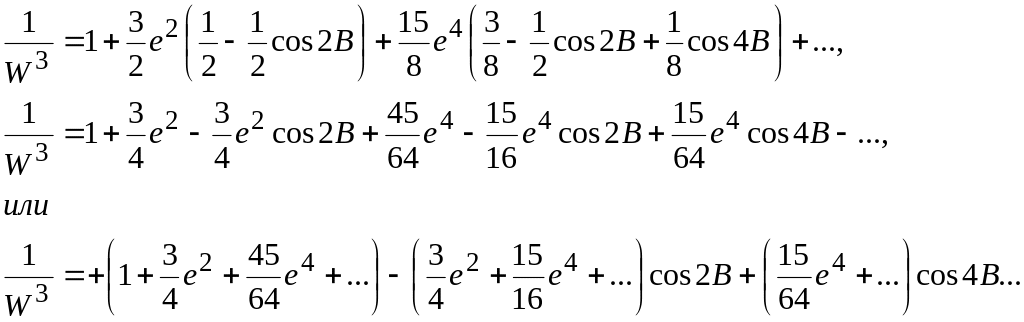 Подставляя найденное значение 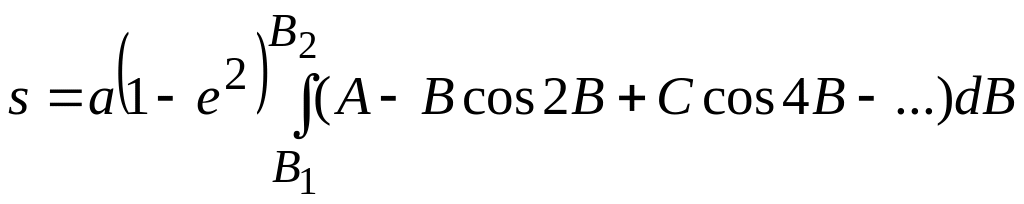 . Интегрируя почленно, найдем:  . Примем: 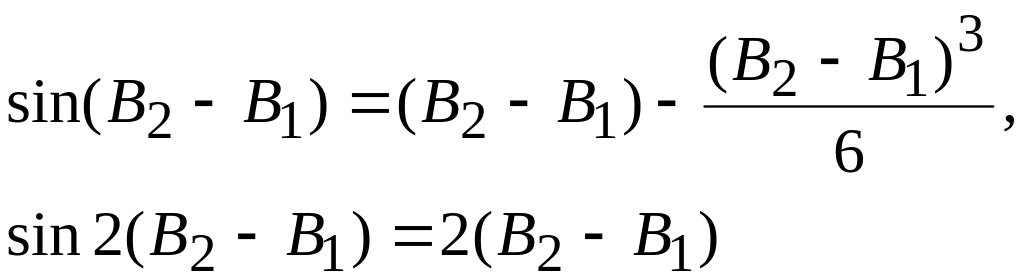 (как стоящий при коэффициенте с е5) и введем среднюю широту дуги Вm по формуле:  .Получим: 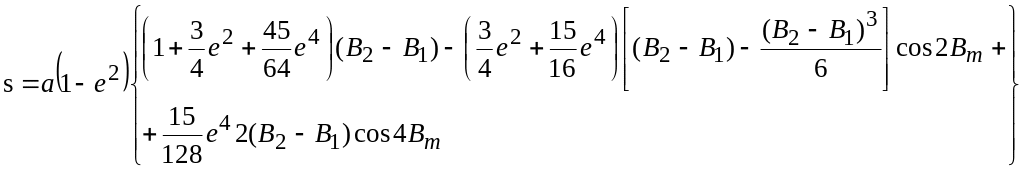 или  Член  , стоящий в последнем выражении, мал: даже при s = 2000 км, что соответствует  , его значение будет равно т. е. этим членом можно пренебречь. Поэтому далее:  ,причем в последнем выражении отброшены малые члены с е7 и е5 (B2 – В1)2. Делая приведение подобных членов по возрастающим степеням е и выражая разность широт в секундах, получим окончательно:  3. Для вычислений в триангуляции, когда стороны незначительны и редко превосходят 50-50 км, дадим более простую и удобную формулу. Обозначим: 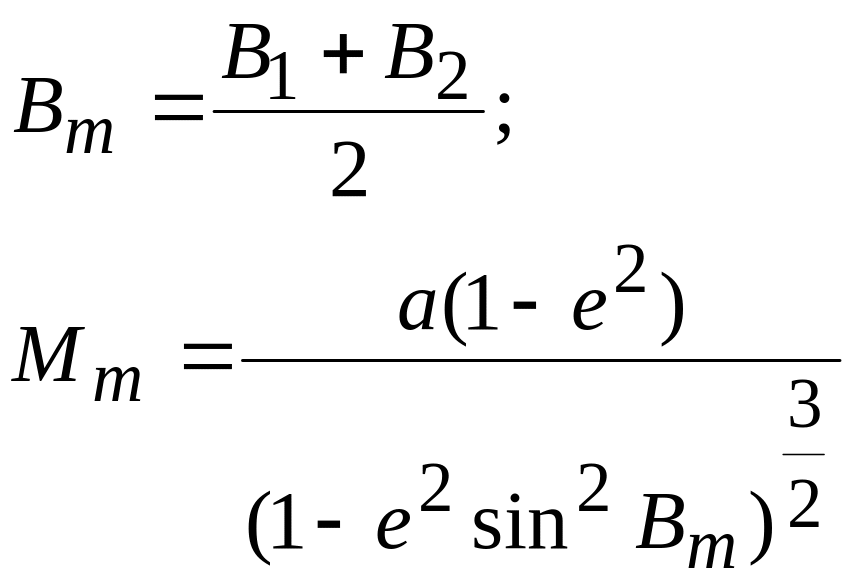 .Введем вспомогательную величину: 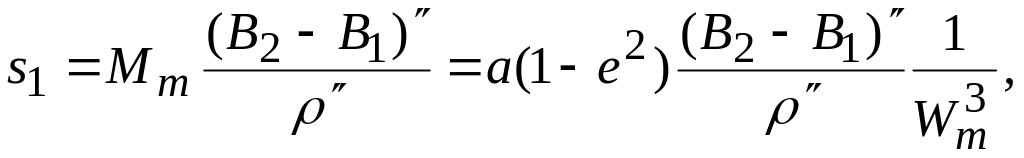 которая, очевидно, представляет собою длину дуги окружности с радиусом, равным радиусу кривизны меридиана в точке со средней широтой данной дуги. Далее напишем:  Подставляем значения коэффициентов А, В, С:   Полагая в поправочном члене последней формулы a(1 — е2) =Mm, т. е. пренебрегая членами порядка  s получим: .Окончательная формула для вычислений в триангуляции имеет вид:  . Формула пригодна для расстояний до 500 км (при s = 500 км допущенная выше погрешность порядка  даст ошибку в значении s, равную приблизительно 1 мм).При s ≤ 55 км значение поправочного члена будет менее 1 мм, поэтому поправочный член в можно отбросить и вычисления вести по формуле:  Следовательно, при длине дуги, меньшей 55 км, ее можно рассматривать как сферическую с центральным углом, равным разности широт ее конечных точек, и описанную радиусом меридианного сечения, соответствующим средней широте дуги. На основании формулы можно решить обратную задачу: зная длину дуги и среднюю широту ее, определить разность широт конечных точек дуги:  . Практически нередко приходится решать следующую задачу. Даны широта первой точки В1, расстояние по дуге меридиана до второй точки s; требуется определить широту второй точки В2. Имеем: B2=B1 + (B2 – B1). Для определения (B2 – B1) воспользуемся формулой ; однако сразу по этой формуле искомая разность (B2 – B1) вычислена быть не может, так как неизвестна средняя широта Вm, по которой должен быть рассчитан радиус М или взята из таблиц величина [1]m . Рассмотрим решение задачи с применением метода последовательных приближений. В первом приближении вычисляют (B2 – B1), используя для определения [1] широту первой точки, и получают приближенное значение (B2 – B1)1 = s[1]1, и далее (B2)1 = B1 + (В2— В1)1. С этим значением широты второй точки вычисляют приближенно среднюю широту  , используя найденную приближенную среднюю широту (Вm)1, находят разность широт (B2 — B1)2 и среднюю широту (Вm)2 во втором приближении; далее, аналогично производят вычисления в третьем приближении, четвертом и т. д. до тех пор, пока два смежных приближения не дадут одинаковые результаты в пределах заданной точности, которые и будут окончательными.Таблица 1
Для контроля длина той же дуги может быть вычислена по таблицам для вычисления координат Гаусса. В таблицах приводятся длины дуг меридианов от экватора -до заданных точек через одну минуту. Искомая длина дуги меридиана в определится как разность дуг меридианов х2 и х1от экватора до точек с широтами В2 и В1. Указания о порядке вычислений дуг приведены во введении к упомянутым таблицам. 1-е приближение
2-е приближение
3-е приближение
Так как величина [1]m,соответствующая значению широты Вm полученной для решения задачи в третьем приближении, будет иметь то же значение, что и во втором, то в продолжении вычислений необходимости нет. Искомое значение широты для точки 2 будет В2 = 71°53'39'',059. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||