2 канонические формы. Две канонические формы алгебраической записи логической функции

• Название: Две канонические формы алгебраической записи логической функции
• Дата: 27.03.2019
• Размер: 115.45 Kb.
• Имя файла: 2 канонические формы.docx
• Тип: Документы; #71675
• страница: 1 из 3

3. 
   Две канонические формы алгебраической записи логической функции
   

Логическая функция y(x_v х2,..., хп), заданная таблицей истинности, может быть записана математически в двух канонических видах [6, 7, 9]:

1. 
   совершенная дизъюнктивная нормальная форма (СДНФ) — логическая сумма логических произведений;
   
2. 
   совершенная конъюнктивная нормальная форма (СКНФ) — логическое произведение логических сумм.
   

В обоих видах заключена информация о количестве наборов аргументов, при которых функция у принимает значения 1 и 0, а также о содержании этих наборов. Проиллюстрируем методику получения дизъюнктивной и конъюнктивной канонических форм па примере функции двух переменных по ее таблице истинности (табл. 18.4).

Таблица 18.4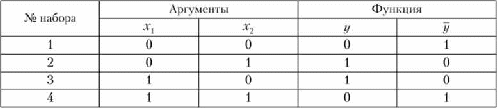


Пример таблицы истинности для функции двух переменных

1. 
   Методика получения СДНФ
   

Дизъюнктивная каноническая форма представляет собой записанное по правилам алгебры логики утверждение о том, что функция y(x_v х₂, ..., х_п) принимает единичное значение только при указываемых наборах аргументов. К такой форме приводят следующие шаги.

1. 
   Из таблицы истинности выделяем наборы аргументов, при которых функция у равна «единице». В табл. 18.4, это строки № 2 и 3.
   
2. 
   Для каждой из выделенных строк записываем логическое произведение, в котором представлены все п аргументов набора. Аргумент x_i присутствует «собственной персоной», если в рассматриваемом наборе он равен 1. Если же в данном набореx_i = 0, он учитывается в виде инверсии^-. Таким образом, строкам № 2 и 3 табл. 18.4 соответствуют произведения х_{ •х2; х_{ -х₂.
   
3. 
   Составляем логическую сумму записанных произведений: y(x_lt х₂) = = x_t-x₂ + .г₁-х2.
   

Эта сумма и является искомым алгебраическим выражением функции у в совершенной дизъюнктивной нормальной форме (СДНФ).

Отметим характерные признаки СДНФ: число слагаемых равно числу «единиц» в столбце у таблицы истинности; каждое слагаемое есть произведение из п сомножителей, где п — число аргументов.

2. 
   Методика получения СКНФ
   

Один из способов нахождения конъюнктивной канонической формы заключается в применении методики, изложенной в подпараграфе 18.3.1, к инверсии заданной логической функции у с последующим преобразова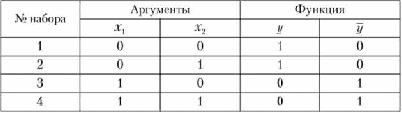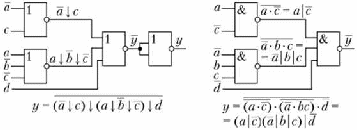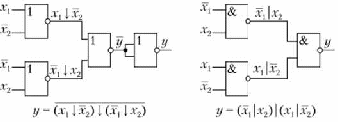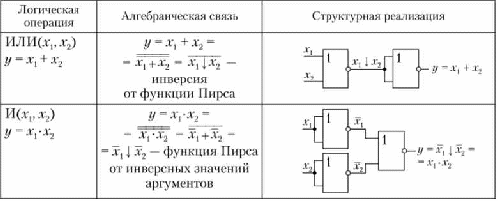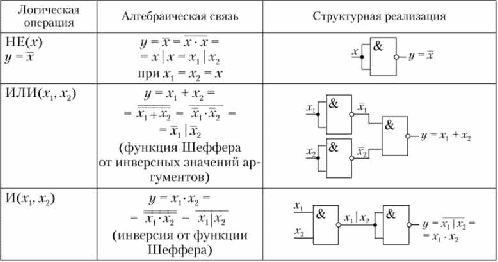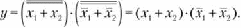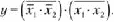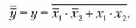




нием по теореме де Моргана. Проиллюстрируем его на примере данных табл. 18.4.

1. 
   От функции у переходим к ее инверсии у, заменив в столбце у (см. табл. 18.4) «нули» на «единицы» и наоборот.
   
2. 
   Записываем дизъюнктивную каноническую форму функции у по методике, рекомендованной в подпараграфе 18.3.1 (выделив наборы аргументов для единичных значений у)\ у = х_{ •х₂ + х_{ •х₂.
   
3. 
   Находим инверсию от найденного алгебраического выражения:
   

4. 
   Преобразуем записанное равенство по формуле де Моргана, заменив инверсию суммы произведением инверсий (а + b = а-Ь):
   

Пользуясь той же формулой, произведения х_х •х₂ и х_{ •х₂ заменяем эквивалентными суммами, а именно х_{ • х₂ ⁼ х_{ + х2; х₁-х₂ = х₁+х₂. И наконец, для функции у получаем следующее выражение:


Оно имеет совершенную конъюнктивную нормальную форму — логическое ироизведеиие логических сумм. Обратим внимание на то, что число сомножителей в получаемом произведении равно числу «нулевых» значений функции у, заданных в таблице истинности. А каждый сомножитель есть сумма п слагаемых, где п — число аргументов.

Следствием рассмотренной нами методики получения СКНФ является ее укороченный вариант [6, 121. Он содержит такие действия.

В столбце у таблицы истинности выделяем строки, где функция у принимает «нулевое» значение.

Для каждой такой строки записываем логическую сумму, включающую «представителей» всех аргументов набора. Причем аргумент x_i записывается в неинвертированном виде, если в данном наборе x_i = 0. Если же х- = 1, то в логической сумме присутствует его инверсия х_г

Найденные логические суммы перемножаем и сразу приходим к выражению для функции у в совершенной нормальной конъюнктивной форме (СКНФ).

В рассматриваемом нами случае по таблице истинности 18.4 записываем у = (хj + х₂) • (х, + х₂), что совпадает с ранее полученным результатом.

Пример 18.1. Для логической функции трех переменных у(л\ух₂,х^), заданной таблицей истинности (табл. 18.5), получить алгебраические выражения в совершенных нормальных формах: дизъюнктивной и конъюнктивной.

Решете

1. 
   Совершенная дизъюнктивная нормальная форма. В соответствии с изложенной в подпараграфе 18.3.1 методикой выполняем следующие операции.
   

По табл. 18.5 находим наборы аргументов, при которых у = 1. Это строки № 3, 5, 7:

№ 3: х_х = 0; х₂ = 1; х₃ = 0;

№ 5: х_х = 0; х₂ = 0; х₃ = 1;

№ 7: х_х = 0; х₂ = 1; х_:1 = 1.

Таблица 18.5 К примеру 18.1 №	Аргументы			Функция У
	*\	х2	х3
1	0	0	0	0
2	1	0	0	0
3	0	1	0	1
4	1	1	1	0
5	0	0	1	1
6	1	0	1	0
7	0	1	1	1
8	1	1	0	0

Для указанных наборов записываем логические произведения «представителей» аргументов:

N° 3 -*■ х, ■ х2• х3; № 5 —► х, • х2• х3; № 7 —* х, -х2-х3.

Логическая сумма составленных произведений является искомой совершенной дизъюнктивной нормальной формой функции y(x_vx₂>x3):

y(x_v х2, х3) = x_i -х₂-х₃ + х\ • х₂ • х₃ + х, *х₂ *х3.

2. 
   Совершенная конъюнктивная нормальная форма. Воспользуемся рекомендованной в подпараграфе 18.3.2 укороченной методикой.
   

В таблице истинности выделяем строки, где у = 0:

№ 1 (0, 0, 0); № 2 (1, 0, 0); № 4 (1,1, 1); № 6 (1, 0, 1); № 8 (1, 1, 0).

Л ля каждой из выделенных строк записываем логическую сумму «представителей» всех аргументов:

№ 1 —<► х, + х₂ + х3; № 2 —► х, + х₂ + х3; № 4 —*► x_t + х₂ + х3;

№ 6 —*• х, + х₂ + х3; № 8 —*■ х, + х₂ + х3.

3. 
   Перемножим записанные логические суммы и приходим к выражению функции y(x_v х2, х3) в совершенной конъюнктивной нормальной форме:
   

у(рс,, х2, х^) = (х, + х₂ + х^) • (х, + х₂ + х3) • (х, + х₂ + х3) •

• (Xj + X, + х3) • (Х[ + X, + х3).

В приведенном примере конъюнктивная форма является более громоздкой, чем дизъюнктивная. Этот результат понятен, так как в столбце у табл. 18.5 «нулей» больше, чем «единиц». Если в табличном представлении функции у число «нулей» меньше числа «единиц», то конъюнктивная форма проще дизъюнктивной.

3. 
   Минимизация логических функций