движение тела под действием силы тяжести. Движение тела под действием силы тяжести
 Скачать 54.72 Kb. Скачать 54.72 Kb.
|
|
Тема: Движение тела под действием силы тяжести Цель урока: изучить законы падения тел под действием силы тяжести. Новый материал Законы падения тел интересовали людей с древних времен. Казалось очевидным, что тяжелые тела падают быстрее легких. А что показывает опыт? На дно стеклянной трубки поместим дробинку, кусочек пробки и птичье перышко. Перевернем трубку. Быстрее всех падает дробинка, медленнее всех — перышко (рис. 177, а). Означает ли это, что тяжелые тела всегда падают быстрее легких? Не торопитесь с ответом. Откачаем из трубки воздух (рис. 177, б) и перевернем ее снова. Теперь дробинка, пробка и перышко достигают дна одновременно (рис. 177, в). Движение тел было различным из-за сопротивления воздуха. Как только сопротивление стало пренебрежимо малым, тела разных масс стали двигаться одинаково. Вывод о том, что различие во времени падения тел вызвано сопротивлением воздуха, а не различием масс, сделал Галилей в конце XVI в. Опыт с телами, падающими в трубке, из которой откачан воздух, был проведен Ньютоном. Движение тела, на которое действует только сила тяжести, называется свободным падением. Современные, имеющие высокую точность эксперименты подтверждают: ускорения всех свободно падающих тел в данном месте одинаковы. Как объяснить такую удивительную закономерность? Для этого достаточно применить второй закон Ньютона и учесть, что сила тяжести прямо пропорциональна массе тела. 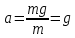 . .Мы доказали, что модуль ускорения свободного падения для всех тел одинаков, и выяснили, что коэффициент g равен модулю ускорения свободного падения. При этом ускорение свободного падения направлено так же, как сила тяжести вертикально вниз. Значение g характеризует ускорение свободного падения на средних географических широтах. Зависимость ускорения свободного падения от широты связана с вращением Земли вокруг своей оси и «сплюснутостью» Земли у полюсов. При удалении от земной поверхности значение g постепенно уменьшается. Движение тел под действием силы тяжести изучает баллистика (греч. бросаю). Она рассматривает движение артиллерийских снарядов, пуль, авиационных бомб, баллистических ракет и т. д. В точных баллистических расчетах, кроме влияния силы тяжести, учитывается сопротивление воздуха и ряд других факторов. Пренебрежение сопротивлением воздуха для достаточно массивных тел малых размеров при небольшой скорости движения (брошенный камень, спортивное ядро и др.) не приведет к серьезной ошибке. В других случаях (волейбольный мяч, артиллерийский снаряд, пуля) пренебрегать сопротивлением воздуха недопустимо. Траектория и другие характеристики движения свободно падающего тела зависят от положения начальной точки, от угла, под которым направлена начальная скорость, и от ее модуля. На рисунке 178 представлены различные случаи свободного падения тела, брошенного: а) с высоты Н вертикально вниз; б) с поверхности Земли вертикально вверх; в) горизонтально; г) под углом к горизонту. Тело, падающее с высоты h без начальной скорости. Движение шарика будет прямолинейным, равноускоренным. 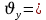 ; ; 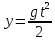 . .Если принять 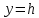 , то , то 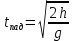 , , 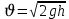 . .Тело, брошенное горизонтально. Шарик движется по криволинейной траектории. При этом он участвует одновременно в двух движениях: перемещается вправо по горизонтали и снижается по вертикали. Вдоль оси Ox движение равномерное, оси Oy ‒ равноускоренное. 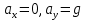 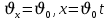 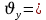 ; ; 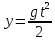 . .Время полета шарика в случае 1 (с некоторой высоты) и 2 (брошенного горизонтально) одинаково! Оно равно 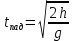 и не зависит от начальной скорости. и не зависит от начальной скорости.Найдем горизонтальную дальность полета: 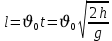 Скорость движения шарика в каждой точке направлена по касательной к траектории 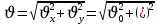 . .В конце полета 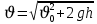 Траекторией движения является участок параболы с вершиной в точке бросания. Тело, брошенное вертикально вверх. Шарик движется прямолинейно: равнозамедленно при подъеме и равноускоренно при спуске. 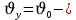 ; ; 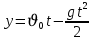 . .Найдем время подъема, приравняв 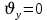 : : 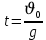 , и полное время полета, приравняв , и полное время полета, приравняв 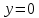 : : 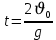 . .Максимальная высота подъема 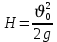 . .Т 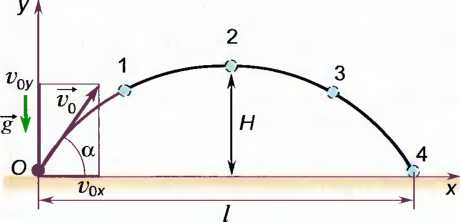 ело, брошенное под углом к горизонту. 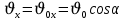 , , 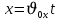 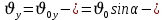 , , 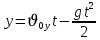 Максимальная высота подъема 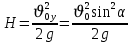 Время подъема на эту высоту 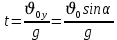 Время полета 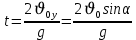 Горизонтальная дальность полета 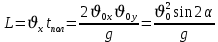 |
