Имитационное моделирование двухканальной системы обслуживания. Лабораторная 3. Отчёт. Двухканальная система массового обслуживания по дисциплине Моделирование процессов и систем
 Скачать 3.62 Mb. Скачать 3.62 Mb.
|
|
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ) КАФЕДРА ИНФОРМАЦИОННЫХ СИСТЕМ И ТЕХНОЛОГИЙ ОТЧЁТ по лабораторной работе №3 на тему: «Двухканальная система массового обслуживания» по дисциплине «Моделирование процессов и систем» Выполнила студентка группы ИСТ-032: Мартынова Е.С. «___» ________ 2022г. __________/__________/ Принял: к. т. н. доцент ИУС, Козлова Л. П. «___» ________ 2022 г. ________/Л. П. Козлова/ Санкт-Петербург 2022 Содержание Содержание 2 Введение 3 Цель работы: 3 Задачи: 3 Основная часть 4 Ход работы: 4 Задание 1 4 Задание 2 5 Задание 3 7 Задание 4 8 Вывод 10 Введение Цель работы: Научиться выполнять имитационное моделирование двухканальных систем массового обслуживания. Задачи: 1. Магазин, располагающий двумя кассами, занимается продажей продовольственных товаров (рис. 2.2). Время между приходом двух покупателей – случайная величина с показательным законом распределения (среднее значение - tz ), а время обслуживания равномерно распределено на интервале [ a ; b ]. Сумма покупки является случайной величиной с нормальным законом распределения (среднее значение - MD ; среднее квадратическое отклонение - SD ). Пусть исходные значения равны величинам: MD =400 руб.; SD =100 руб.; tz =10 мин.; a =3 мин.; b =7 мин.; tn =9 ч. Выполните моделирование поступления семи заявок (покупателей). Определите время прихода седьмого клиента. Какой размер выручки получит магазин а) после того, как было обслужено семь покупателей; б) к моменту времени 10:00 ч.? 2. Предположите, что рассматриваемый поток клиентов – это потенциальные покупатели, которые с вероятностью P могут совершить покупку ( P =0,6) 3. Пусть время обслуживания – дискретная случайная величина со следующим законом распределения Выполните имитацию, учитывая данное условие 4. Проведите 10 экспериментов и рассчитайте величины: - среднее время ожидания; - средний размер выручки Основная часть Ход работы: Задание 1 Построим таблицу и вставим в неё формулы равномерного, нормального, и показательного распределений. Время прибытия заявки рассчитывается: Время обслуживания рассчитывается: Начало обслуживания по каналу 1: Конец обслуживания по каналу 1: Начало обслуживания по каналу 2: Конец обслуживания по каналу 2: Выручка рассчитывается: Время прихода 7-го клиента: Сумма покупок после 7 клиентов: Сумма покупок к 10:00: После вычисления всех значений получаем таблицы:  Рис. 1 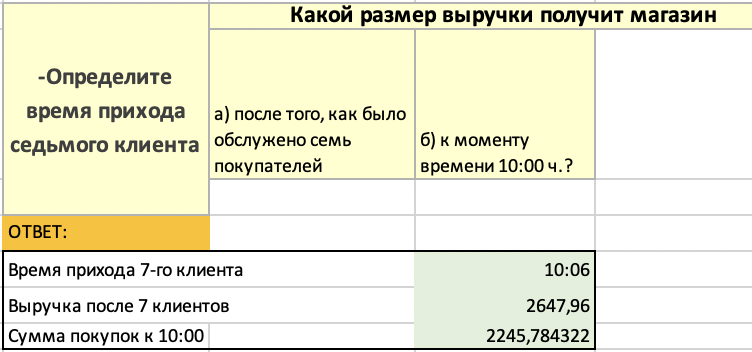 Рис. 2 А также диаграммы, соответствующие расчётам:  Рис. 3 Таким образом, время прихода последнего клиента равно 10:06, выручка после 7 клиентов – 2647.96, а сумма покупок к 10:00 составляет 2245.78. Задание 2 Добавим столбец с вероятностью покупки товара. Его формула: И добавим столбец с выручкой если купит. Его формула:  Рис. 4  Рис. 5 Изменим формулу расчета суммы покупки после 7 клиентов, используя столбец предполагаемой выручки: 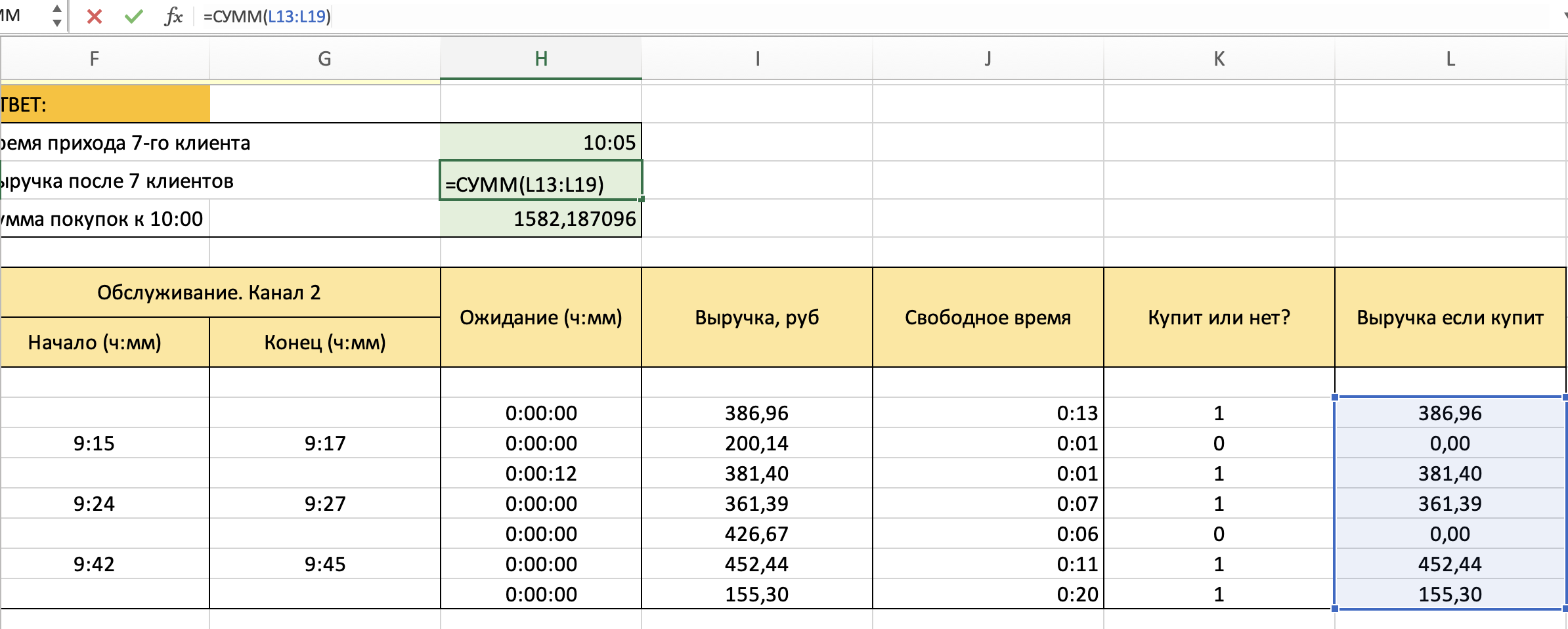 Рис.6 Аналогично для суммы покупок к 10:00: Новые расчёты привели к результатам:  Рис. 7 Посчитаем Биноминальное распределение: И Пуассоновское распределение: Получаем следующую таблицу: 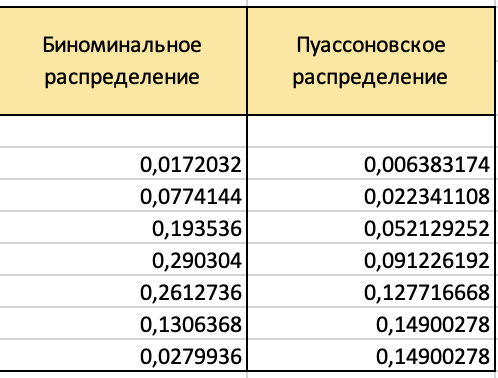 Рис. 8 Визуализируем результаты: 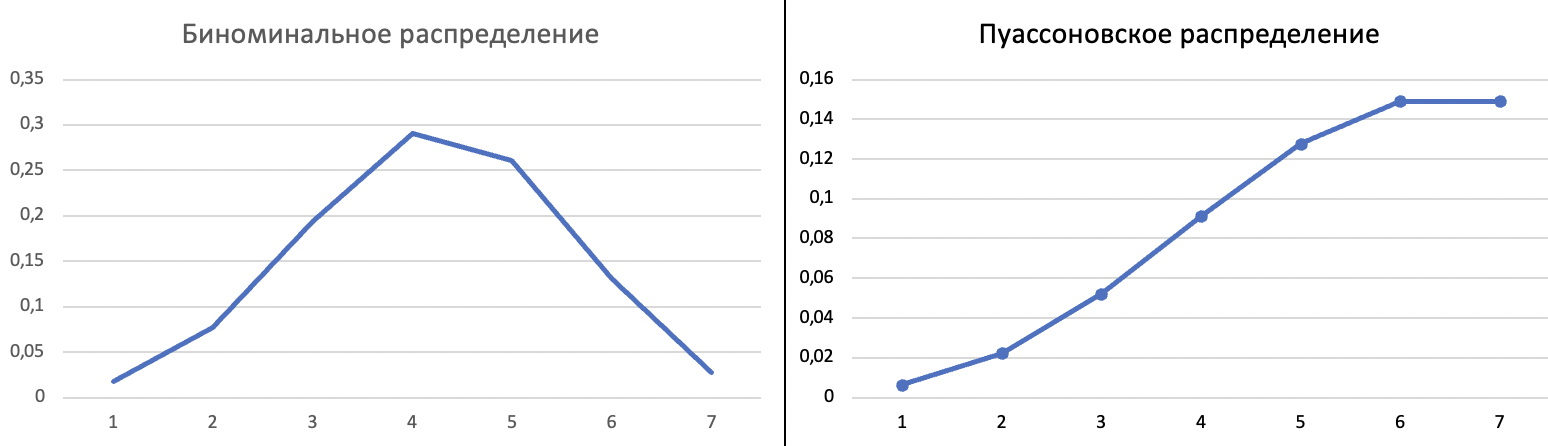 Рис.9 Новые расчёты привели к результатам:  Рис. 10 Таким образом, время прихода последнего клиента равно 10:44, выручка после 7 клиентов – 1363.09, а сумма покупок к 10:00 составляет 996.48. Задание 3 Создадим доп. графы для вычисления пуассоновского и биноминального распределения. Так как у нас всего 4 значения, наша лямбда будет равна 4. Итак, формула для обоих распределений:  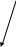 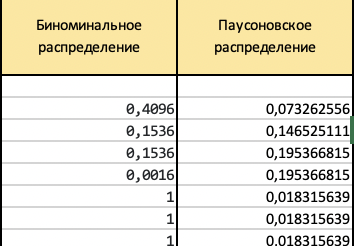 Рис. 11 Время обслуживания будет рассчитываться: В результате вычислений получилась следующая таблица и результаты:  Рис. 12 Визуализация результата:  Рис. 13 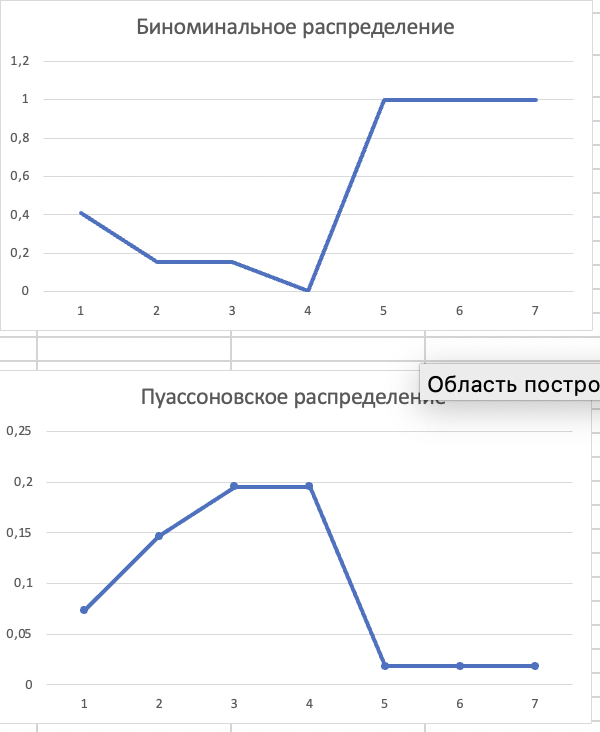 Рис.14 Таким образом, время прихода последнего клиента равно 10:11, выручка после 7 клиентов – 1479.23, а сумма покупок к 10:00 составляет 1257.66. Задание 4 Проведем 10 экспериментов: 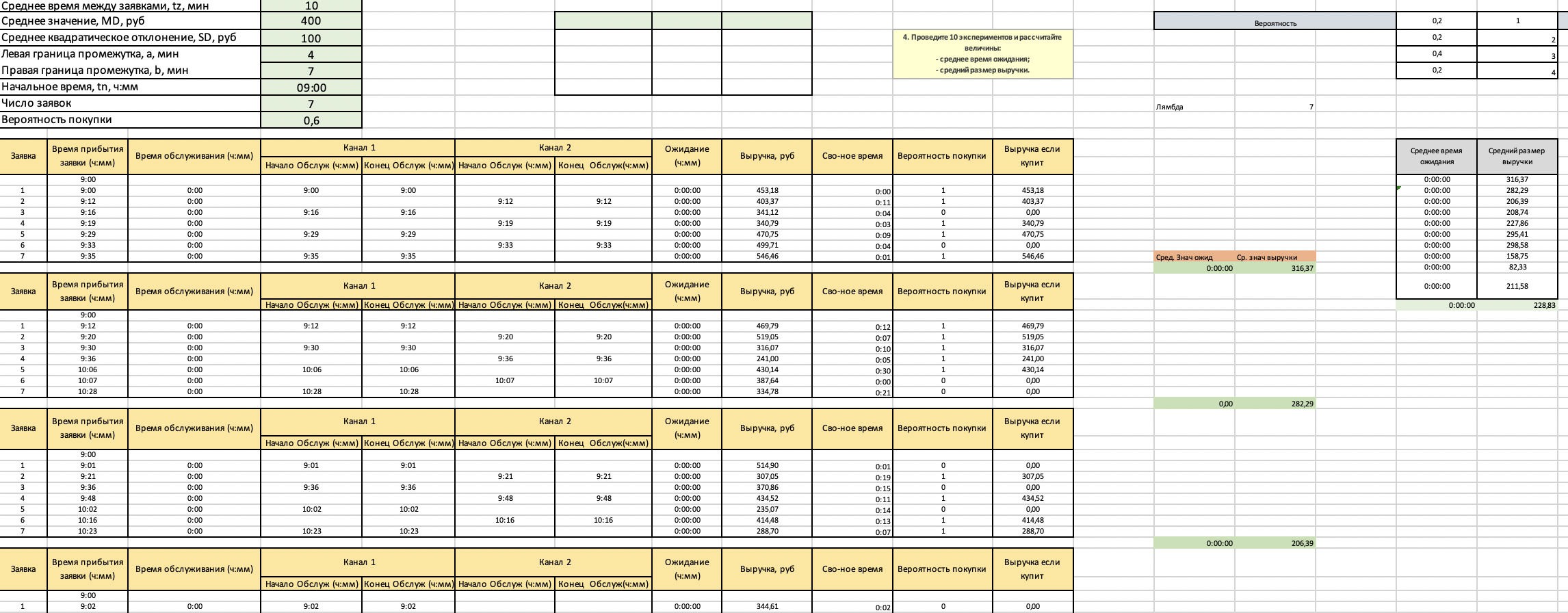 Рис. 15 Вычислим среднее время ожидания для каждого эксперимента: 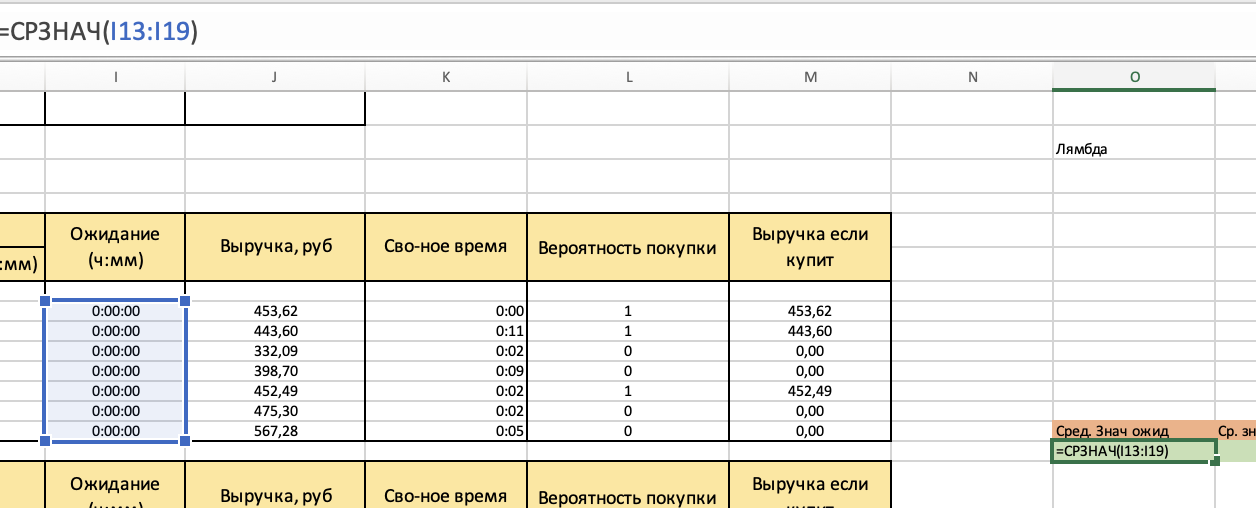 Рис. 16 А затем среднее время ожидания и доход среди всех 10-ти экспериментов: 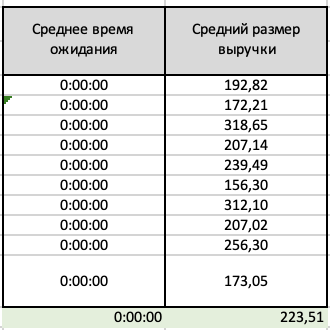 Рис. 17 Таким образом получаем 10 экспериментов и вычислив среднее время ожидания среди всех экспериментов и среднюю сумму выручки – получили соответственно – среднее время ожидания = 0.00, а средняя выручка = 223.51. Вывод В ходе проделанной работы были получены навыки имитационного моделирования двухканальной системы массового обслуживания, в результате которого была выполнена имитация работы магазина, располагающим двумя кассами. |
