9.5.4. Точка пересечения и расчет уровней
интермодуляционных продуктов на нелинейном элементе
Для того чтобы понять, что такое точка пересечения определенного порядка, рассмотрим ситуацию, когда на вход нелинейного прибора поступают два тональных (гармонических) сигнала, т. е.
uвх(t) = U1 cos (1t) + U2 cos (2t), (9.18)
а характеристика нелинейного прибора описывается полиномом М-й степени с постоянными коэффициентами, так что связь между выходом и входом прибора определяется выражением (9.2):
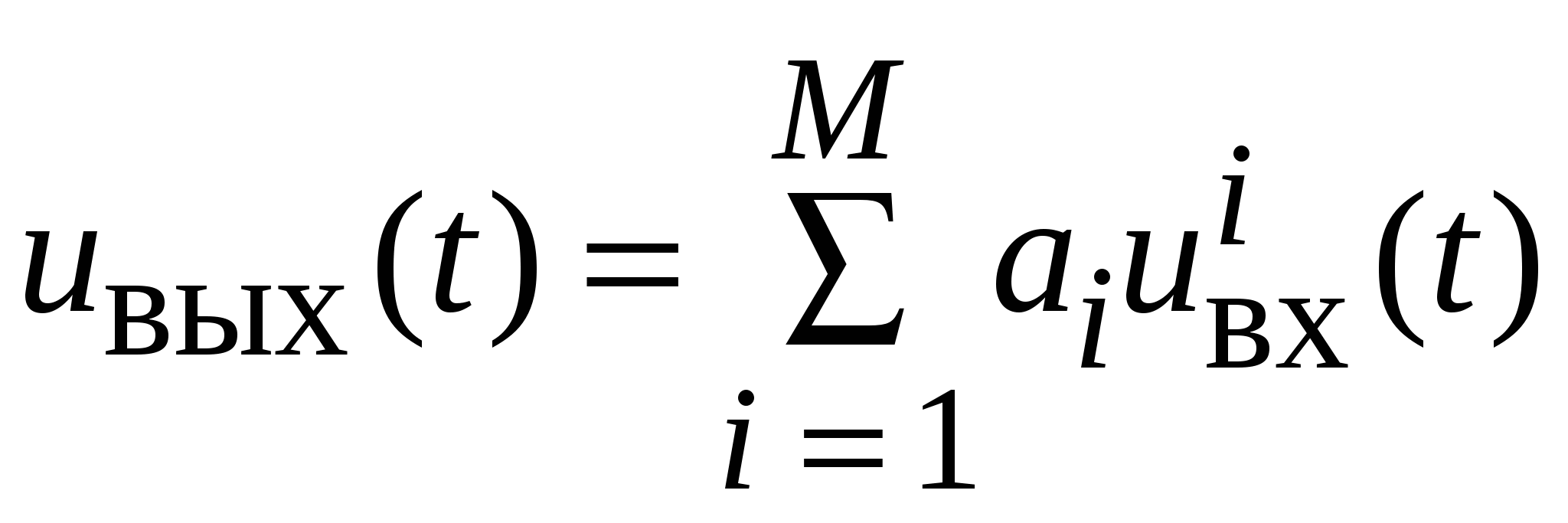 . (9.2) . (9.2)
Пусть интерес представляют амплитуды интермодуляционных продуктов N-го порядка (N ≤ M) c частотами
fим = | (N– k)f1 kf2 |
или
им = | (N– k)1 k2 |, (9.19)
где N, k – целые положительные числа и N > k.
Допустим, далее, что интермодуляцию порядка N порождает только член полинома (9.2), имеющий степень N. Это допущение дает достаточно точные для практики результаты, если суммарная мощность рассматриваемых сигналов не превышает точки компрессии 1 дБ по входу. В таком случае для решения поставленной задачи достаточно в выражении (9.2) рассмотреть только член N-й степени, подставив в него (9.18). Этот член имеет вид
аN (U1 cos (1t) + U2 cos (2t))N. (9.20)
Раскрыв (9.20) по правилам вычисления бинома Ньютона, из всех слагаемых выделим слагаемое, в котором члены бинома имеют степени, отвечающие коэффициентам искомой комбинации частот (9.19), т. е. (N– k) и k. Этим слагаемым будет
aN 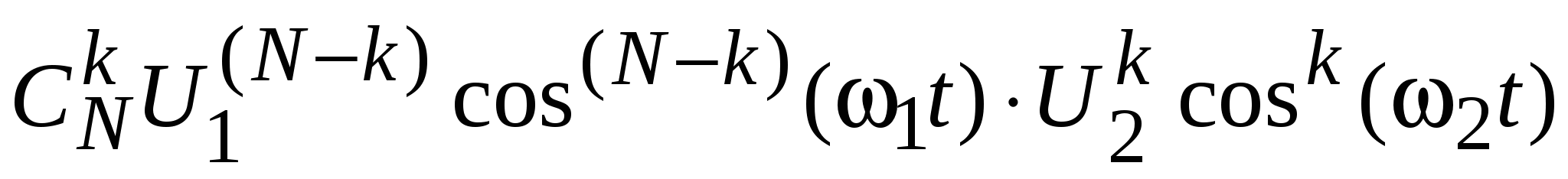 , (9.21) , (9.21)
где  – число сочетаний из N по k. – число сочетаний из N по k.
Учитывая, что разложение cosn(x) имеет вид
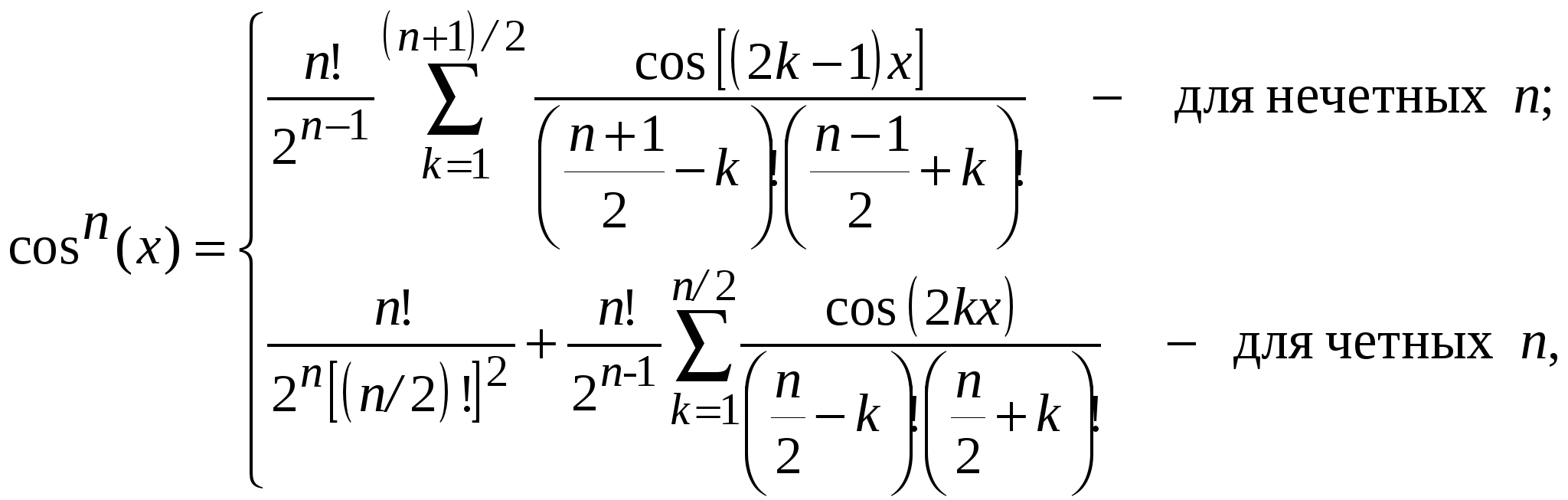
и для любого целого положительного n его можно представить как
cosn(x) = 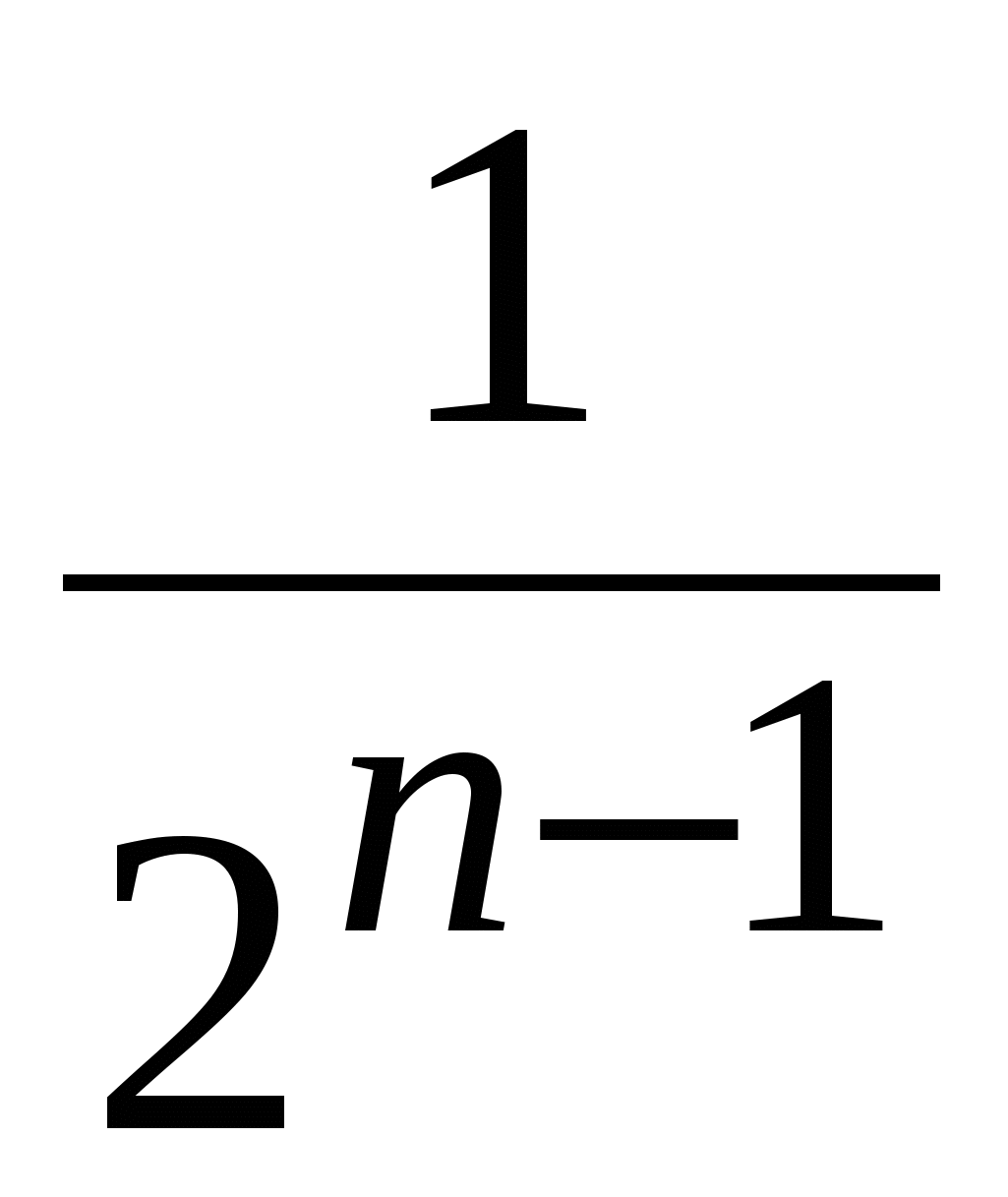 {cos (nx) + 2 cos [(n2)x] + 4 cos [(n4)x] + …}, {cos (nx) + 2 cos [(n2)x] + 4 cos [(n4)x] + …},
где 2, 4, …– целые положительные или отрицательные числа, выражение (9.21) можно переписать в виде
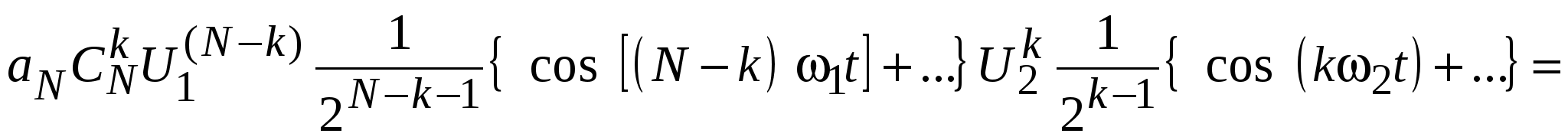
=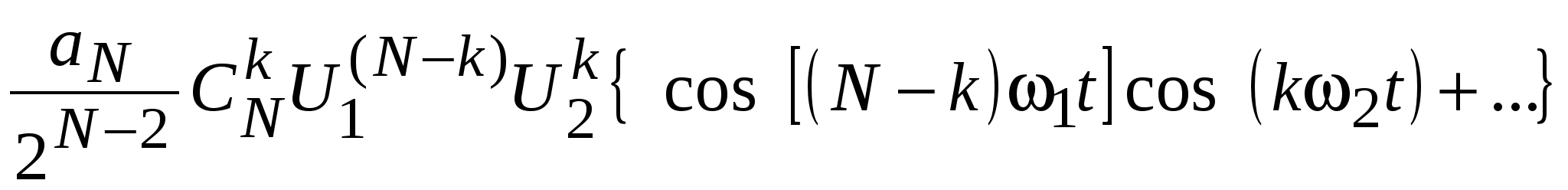 . .
Выделенное в этом выражении слагаемое порождает интересующую частоту и порядок интермодуляции. Все другие произведения дадут порядки меньше, чем N. Поскольку
сos [(Nk)1t] cos (k2t) = 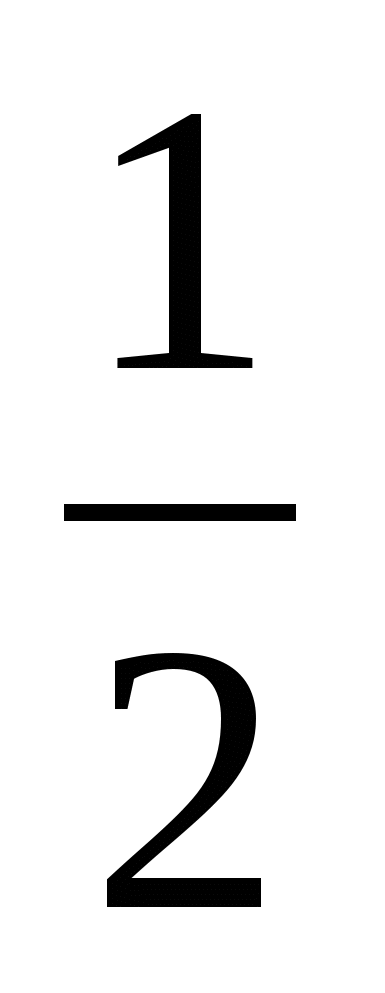 {cos [((Nk)1k2)t] + cos [((Nk)1+ k2)t]}, {cos [((Nk)1k2)t] + cos [((Nk)1+ k2)t]},
то для интересующей амплитуды интермодуляционного продукта N-го порядка Uим N , соответствующей частоте интермодуляции (9.19), получим
Uим N = 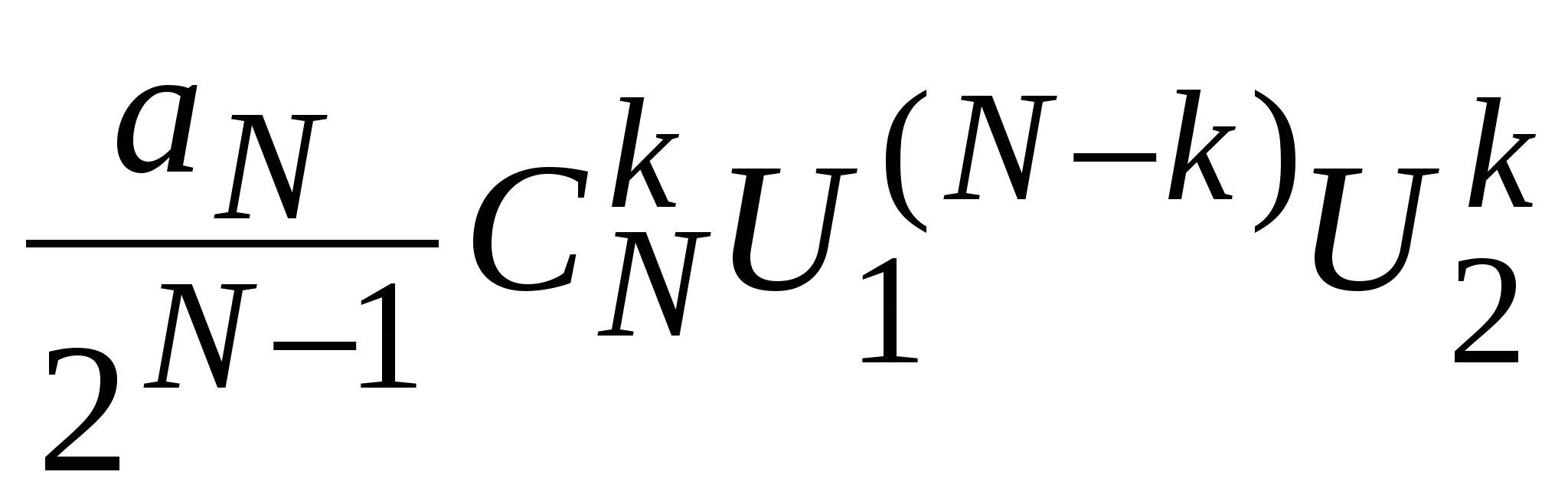 , (9.22) , (9.22)
или, переходя к форме записи в децибелах,
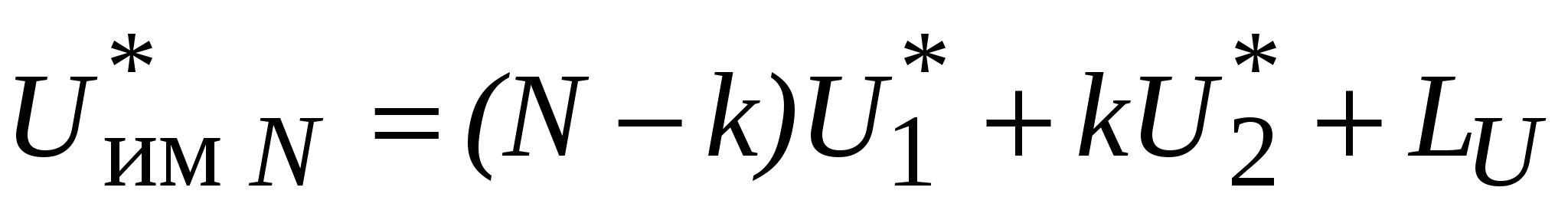 . (9.23) . (9.23)
Здесь 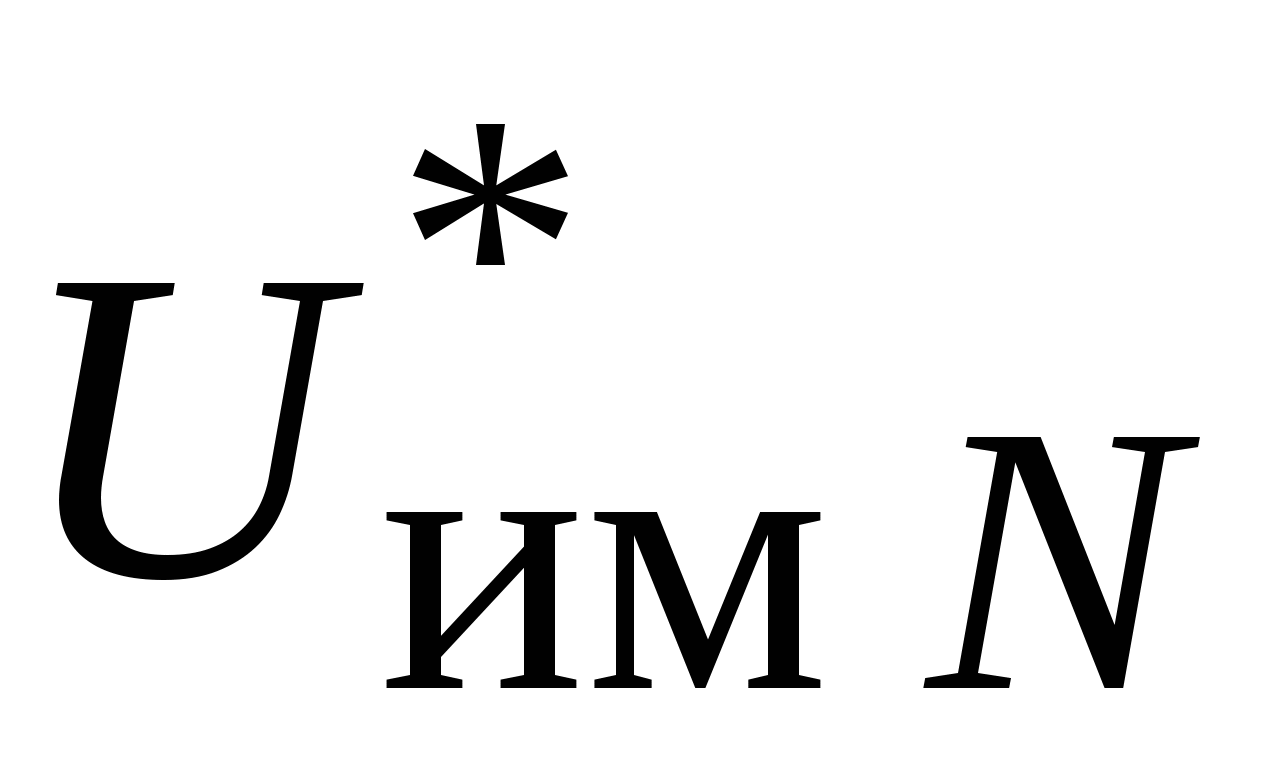 амплитуда ИМП N-го порядка с частотой (9.19), образующаяся на нелинейности вида (9.2), выраженная в децибелах относительно некоторого опорного уровня (обычно относительно 1 мкВ); амплитуда ИМП N-го порядка с частотой (9.19), образующаяся на нелинейности вида (9.2), выраженная в децибелах относительно некоторого опорного уровня (обычно относительно 1 мкВ); 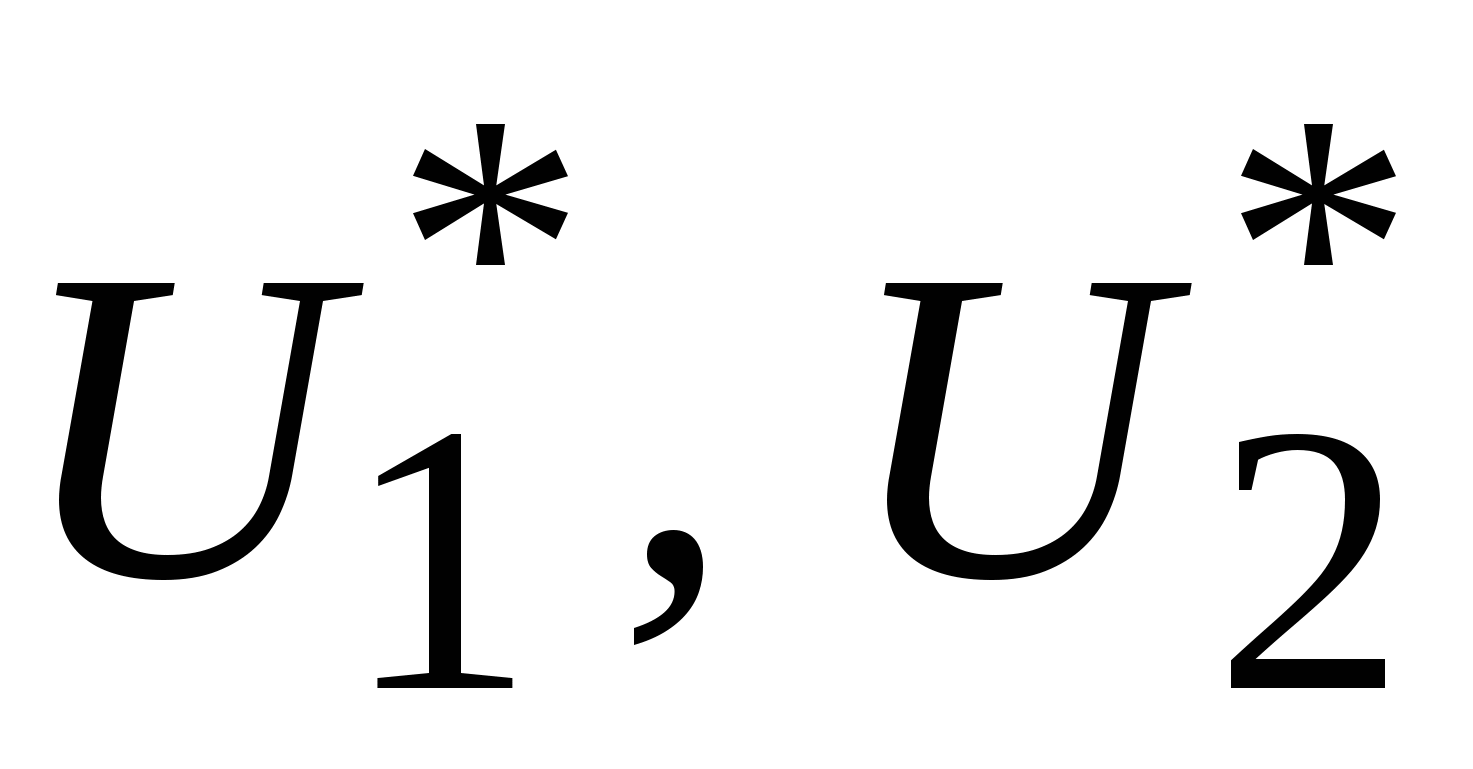 амплитуды сигналов на входе нелинейного прибора, выраженные в тех же единицах, что и амплитуды сигналов на входе нелинейного прибора, выраженные в тех же единицах, что и 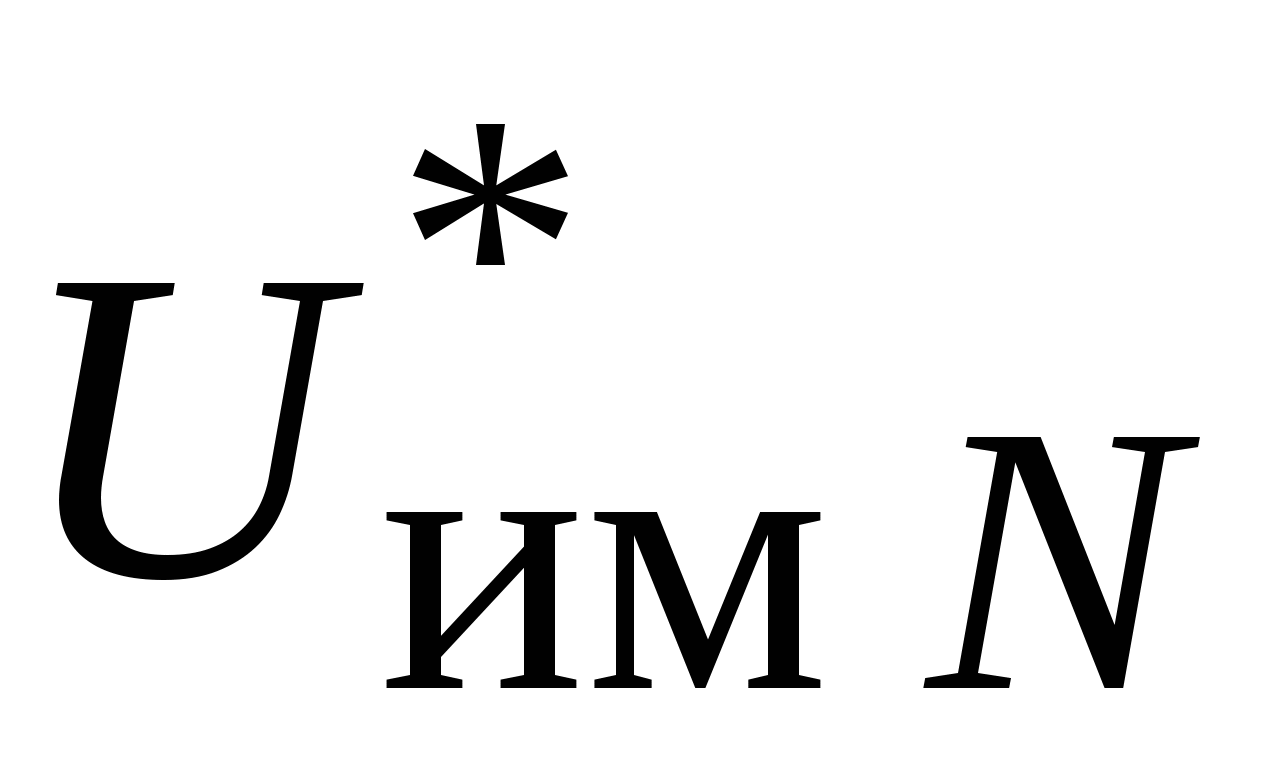 ; LU потери преобразования по напряжению, представленные в (9.22) постоянным множителем, которые зависят от порядка интермодуляции, дБ. ; LU потери преобразования по напряжению, представленные в (9.22) постоянным множителем, которые зависят от порядка интермодуляции, дБ.
Выражение (9.22), связывающее амплитуды входных сигналов и амплитуду интермодуляционного продукта, можно преобразовать в выражение, связывающее мощности указанных сигналов. Для мощностей, представленных в децибелах (обычно в децибелах относительно 1 мВт, дБм), получим
PIMN = (Nk)P1 + kP2 + LP, (9.24)
где PIMN– мощность ИМП N-го порядка, дБм; P1, P2 – мощности входных сигналов, дБм; LP – потери преобразования по мощности, дБ.
Выражение, связывающее мощности сигналов основной частоты на входе и выходе прибора, имеет вид
Pс. вых = Pс. вх + G, (9.25)
где Pс. вх и Pс. вых – мощности сигналов на входе и выходе прибора соответственно, дБм; G – коэффициент усиления прибора по мощности, дБ.
Так как коэффициент усиления прибора G в линейном режиме является величиной постоянной, то из выражения (9.25) следует, что увеличение (уменьшение) уровня сигнала на входе прибора на 1 дБ вызывает увеличение (уменьшение) сигнала на выходе также на 1 дБ, т. е. скорость изменения уровня выход/вход составляет 1 дБ/дБ.
При допущениях, сделанных при получении соотношений (9.23) и (9.24), потери преобразования, фигурирующие в этих формулах, являются постоянными величинами. Тогда, как следует из (9.23) и (9.24), одновременное увеличение (уменьшение) каждого сигнала, формирующего интермодуляционный продукт N-го порядка, на 1 дБ приводит к увеличению (уменьшению) уровня этого продукта на N дБ, т. е. на порядок интермодуляции. Скорость изменения выход/вход в этом случае составляет N дБ/дБ.
П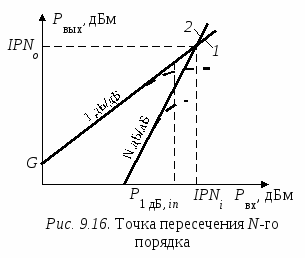 редставим соотношения (9.24) и (9.25) на графике, полагая в (9.24) P1 = P2. Это представление показано на рис. 9.16. Прямая 1 имеет наклон 1дБ/дБ и соответствует уравнению (9.25) для идеального линейного усилителя. Прямая 2 имеет наклон N дБ/дБ и соответствует уравнению (9.24), неограниченно продолженному для уровней мешающих сигналов, образующих ИМП N-го порядка. Интермодуляционный продукт на выходе нелинейного прибора появляется, когда уровни сигналов его образующие имеют значительную мощность, однако растет он быстрее, чем уровень сигнала на основной частоте. В результате графики, представленные уравнениями (9.24) и (9.25) пересекаются в некоторой точке, которая называется точкой пересечения N-го порядка (т. е. порядка рассматриваемой интермодуляции). редставим соотношения (9.24) и (9.25) на графике, полагая в (9.24) P1 = P2. Это представление показано на рис. 9.16. Прямая 1 имеет наклон 1дБ/дБ и соответствует уравнению (9.25) для идеального линейного усилителя. Прямая 2 имеет наклон N дБ/дБ и соответствует уравнению (9.24), неограниченно продолженному для уровней мешающих сигналов, образующих ИМП N-го порядка. Интермодуляционный продукт на выходе нелинейного прибора появляется, когда уровни сигналов его образующие имеют значительную мощность, однако растет он быстрее, чем уровень сигнала на основной частоте. В результате графики, представленные уравнениями (9.24) и (9.25) пересекаются в некоторой точке, которая называется точкой пересечения N-го порядка (т. е. порядка рассматриваемой интермодуляции).
Различают точку пересечения, отнесенную к входу, IPNi, и точку пересечения, отнесенную к выходу, IPNo. Точка пересечения, отнесенная к входу, соответствует уровню мешающих сигналов на входе, при котором на выходе составляющие на основных частотах взаимодействующих сигналов имеют такую же амплитуду, как и составляющие на частотах интермодуляции рассматриваемого порядка. Точка пересечения, отнесенная к выходу прибора, определяется как уровень на выходе прибора, при котором мощность ИМП рассматриваемого порядка равна мощности на основных частотах на выходе прибора. Значения точек пересечения обычно указывают в децибелах относительно милливатта. Точки пересечения, отнесенные к входу и к выходу, связаны простым соотношением
IPNo = IPNi + G, (9.26)
которое позволяет, зная одну из точек пересечения и коэффициент усиления прибора, рассчитать другую точку пересечения.
В спецификациях на радиоприемные устройства и анализаторы спектра, выпускаемые зарубежными фирмами, а также в международных документах обычно указывают точки пересечения второго и третьего порядков, отнесенные к входу. То же характерно для смесителей. Для усилителей обычно указывают точки пересечения, отнесенные к выходу. Последние являются важным параметром для усилителей мощности и могут быть использованы для оценки уровней интермодуляционных колебаний на выходе радиопередатчиков.
|
 Скачать 3.78 Mb.
Скачать 3.78 Mb.