ряды фурье. Ряды.Ряды Фурье.Сборник задач. Сборник задач по высшей математике. РостовнаДону 2008г. 1

• Название: Сборник задач по высшей математике. РостовнаДону 2008г. 1
• Анкор: ряды фурье
• Дата: 03.05.2023
• Размер: 1.93 Mb.
• Имя файла: Ряды.Ряды Фурье.Сборник задач.doc
• Тип: Сборник задач; #1106375
• страница: 1 из 5

Министерство Транспорта РФ

Филиал ФТОУ ВПО « Морская Государственная Академия

имени Адмирала Ф.Ф. Ушакова » в г. Ростове-на-Дону

Ряды.

Ряды Фурье.

Сборник задач по высшей математике.

Ростов-на-Дону

2008г.
§1. Числовые ряды. Достаточные признаки сходимости ряда и его суммы.

1. 
   Определение ряда и его суммы.
   

Определение 1. Пусть задача бесконечная последовательность чисел.

u₁, u₂, u₃,..., u_n,...

Выражение u₁+u₂+…..+u_n+…. называется числовым рядом

При этом числа u₁, u₂,..., u_n,... называются членами ряда.

Коротко ряд записывается так :

Выражение для n-го члена ряда при произвольном n называется общим членом ряда.

Ряд считается заданным, если известно правило, по которому для любого номера n можно записать соответствующий член ряда. Чаще всего общий член ряда задается формулой , например, если , то ряд имеет вид:

Определение 2. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:

Образуем последовательность частичных сумм ряда:




Определение 3. Если существует конечный предел последовательности частичных сумм членов данного ряда при n

,

то ряд называется сходящимся, а число S-его суммой. Это записывается так.

Если последовательность не стремится к пределу, то ряд называется расходящимся. Это возможно в двух случаях:

1. 
   Если последовательность
   
2. 
   Если последовательность колеблющаяся (т.е. не имеет предела ни конечного, ни бесконечного).
   

В качестве простого примера рассмотрим сумму членов бесконечной геометрической прогрессии:

Сумма n первых членов

Если , то , по этому , т.е.

При бесконечная геометрическая прогрессия образует сходящийся ряд, сумма которого .

a значит, ряд расходится. Если , получится ряд

и т.д., т.е. - колеблющаяся последовательность, не стремящаяся ни к какому пределу, ряд расходится.

Следовательно, бесконечная геометрическая прогрессия представляет ряд, который сходится при и расходится при .
1.2. Свойства сходящихся рядов.
Теория 1. Если ряд сходится и имеет сумму , то ряд

, (2)

где С - какое-либо фиксированное число, также сходится и его сумма равна .

Теория 2 Если сходятся ряды



и их суммы, соответственно, равны и , то также сходятся и ряды



причем их суммы, соответственно, равны и .

Теория 3. Если ряд сходится, то сходится и ряд, полученный из данного путем приписывания или отбрасывания любого конечного числа членов, т.е на сходимость ряда не влияет отбрасывания конечного числа его членов.

3. 
   Необходимый признак сходимости ряда. Гармонический ряд
   

Теорема. Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастание n:

Следствие. Если n-й член ряда не стремится к нулю при n , то ряд расходится.

Например, ряд расходится, т.к.

Рассмотрим гармонический ряд:



Тем не менее, докажем, что ряд расходится.

Напишем гармонический ряд подробнее:



Напишем вспомогательный ряд:



Обозначим сумму n членов гармонического ряда (1), а сумму n членов ряда (2).

Так как каждый член ряда (1) больше или равен соответствующему члену уряда (2), то для



Подсчитаем частичные суммы ряда (2) для n, равных

:

,







Следовательно,

При достаточно большом может быть сделано больше любого положительного числа, т.е.

,

то тогда, поскольку , т.е. гармонический ряд расходится.
1.4 Ряды с положительными членами. Достаточные признаки сходимости.
Будем рассматривать ряды с положительными членами, или, так называемые знакоположительные ряды:



1. Признаки сравнения.

Теорема 1. Пусть имеем двазнакоположительных ряда:



Если хотя бы начиная с некоторого номера n члены ряда (1) не больше соответствующих членов ряда (2): ,

и ряд (2) сходится, то сходится и ряд (1).

Пример. Исследуем на сходимость ряд:

Рассмотрим вспомогательный ряд:

Он сходится как сумма геометрической прогрессии со знаменателем . Сравним его члены с членами исходного ряда:



Очевидно, что . Следовательно, исходный ряд является сходящимся в соответствии с теоремой 1 настоящего пункта.

Теорема 2. Если члены знакоположительного ряда



начиная хотя бы с некоторого номера не меньше соответствующих членов расходящегося знакоположительного ряда.



т.е. , то и ряд (1) расходится.

Пример. Исследуем на сходимость ряд . Запишем его в виде:



Рассмотрим вспомогательный ряд:


Этот ряд расходится, т.к. это гармонический ряд( то, что отброшен первый член, на сходимость не влияет).



Члены ряда (1) не меньше соответствующих членов расходящегося ряда (2), следовательно, по теореме 2 ряд (1) расходится.

Теорема 3. (Предельный признак сравнения.) Если знакоположительные ряды (1) и (2) таковы, что существует конечный предел

,

то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (2) следует расходимость ряда (1).

Предельный признак сравнения чаще всего применяется к рядам, общие члены которых является отношениями многочленов.

При использовании признаков сравнения исследуемый ряд часто сравнивается или с бесконечной геометрической прогрессией (см. п. 1.1), или с обобщенным гармоническим рядом:





который сходится при и расходится при

Пример. Исследовать на сходимость ряды.

1) ; 2)

1) Рядом сравнения будет гармонический ряд . Действительно,

, , ,

следовательно, ряды ведут себя одинаково, а т.к. гармонический ряд расходится, то и данный ряд также расходится.

2) В качестве ряда сравнения выберем обобщенный гармонический ряд , поскольку

Ряд сходится.

( ), поэтому сходится и рассматриваемый ряд.

Из примеров следует вывод:

Чтобы выбрать ряд сравнения, нужно разделить старшую степень числителя на старшую степень знаменателя; образовавшийся после сокращения обобщенный гармонический ряд и есть ряд сравнения.
2. Признак Даламбера.

Если для знакоположительного ряда существует конечный предел



то при 1) L<1 ряд сходится; 2) L>1 ряд расходится; 3) L=1 признак ответа не дает.

Признак Даламбера обычно применяется в том случае, когда общий член ряда содержит факториалы, показательную функцию от n, синус или тангенс бесконечно малого аргумента.

Пример. Исследовать на сходимость:

1) , 2)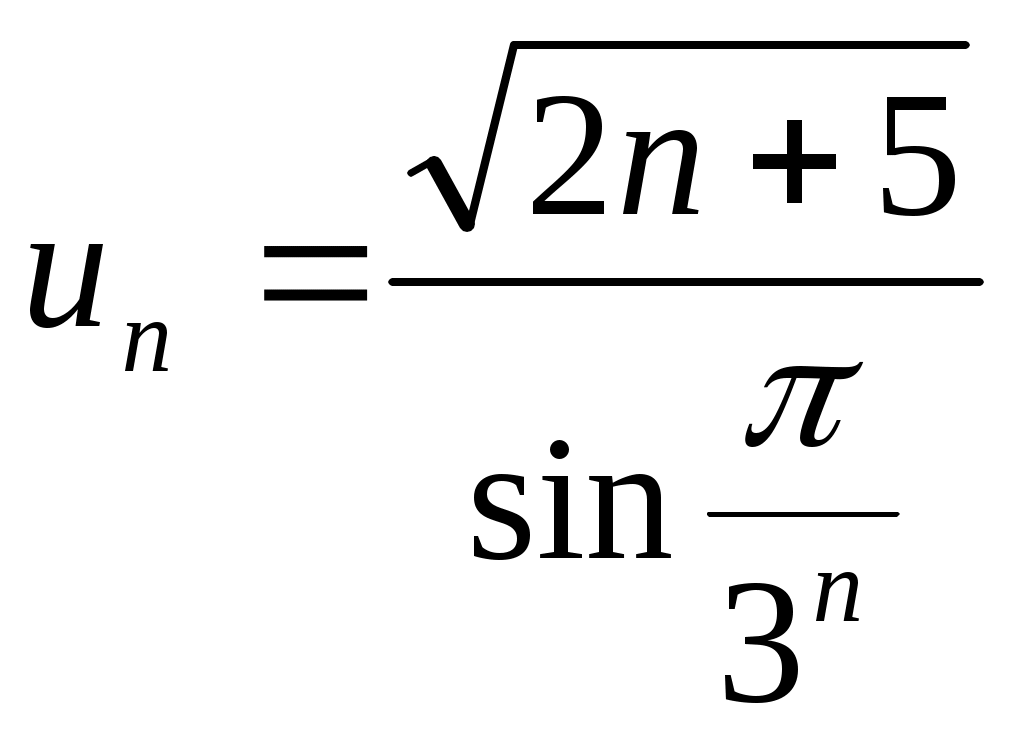

1) Т.к. , то

- ряд расходится.

2) ;

- ряд расходится.
3. Интегральный признак Коши.
Пусть члены ряда u₁, u₂, u₃,..., u_n,... положительны и не возрастают, т.е.

u₁ ≥u₂≥ u₃≥...

и пусть - такая непрерывная невозрастающая функция, что

f(1)=u₁; f(2)=u₂;...; f(n)=u_n

Тогда:

1. 
   если несобственный интеграл сходится, то и ряд сходится;
   
2. 
   если же расходится, то и ряд расходится.
   

Пример. Исследовать на сходимость:
; .

1. 
   Заменяем в заданном выражении общего члена ряда номер n непрерывной переменной x и убеждаемся, что полученная функция
   

является непрерывной и убывающей на всем бесконечном интервале изменения x. Затем находим несобственный интеграл от с бесконечным верхним пределом:



Несобственный интеграл расходится, следовательно, и данный ряд также расходится.

2)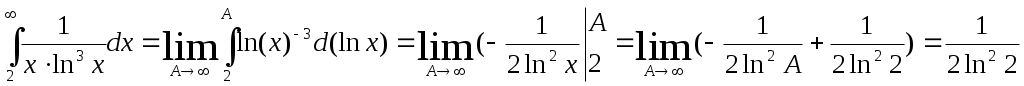
Несобственный интеграл сходится, следовательно, и рассматриваемый ряд также сходится.
4. Радикальный признак Коши.

Если для знакоположительного ряда существует предел ,

то при l<1 ряд сходится, а при l>1 расходится; при l=1 признак ответа не дает.

Пример. Исследовать на сходимость:

1) ; 2)

Решение:

;

.

Следовательно, исходный ряд расходится.

2) ;

,

следовательно, рассмотренный ряд является сходящимся.




Задачи для решения.
В задачах 1-10 написать формулу n-ого члена ряда.

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

В задачах 11-16 написать 5 первых членов ряда

11) .

12) .

13) .

14) .

15) .

16) .

В задачах 17-24 1) найти сумму n первых членов ряда (S_n), 2) доказать сходимость ряда, пользуясь непосредственно определением сходимости и 3) найти сумму ряда (S):

17)

18)

19)

20)

21) .

22)

23)

24)

В задачах 25-30 выяснить, сходится ли данный ряд. Для сходящегося ряда найти его сумму:

25)

26) .

27)

28) .

29)

30) .
В задачах 31-45 исследовать сходимость рядов с помощью признаков сравнения и необходимого признака.

31)

32)

33)

34)

35)

36)

37)

38)

39)
40)

41)

42)

43)

44)

45)
В задачах 46-58 исследовать сходимость рядов с помощью признака Даламбера:
46)

47)

48) .

49) .

50) .

51)

52)

53) .

54) .

55)

56)

57)

58)

В заданиях 59-65 вопрос о сходимости рядов решить с помощью интегрального признака Коши:

59)

60)

61)

62)

63) .

64) .

65) .

В задачах 66-72 исследовать сходимость рядов с помощью радикального признака Коши:

66)

67)

68) .

69) .

70) .

71) .

72) .

В задачах 73-98 исследовать на сходимость ряды:

73) .

74) .

75)

76)

77)

78)

79) .

80) .

81)

82)

83)

84)

85)

86)

87)

88)

89)

90)

91)

92)

93)

94)

95)

96)

97)

98)

§2. Абсолютная и условная сходимость знакопеременных рядов. Признак сходимости знакочередующегося ряда.
Определение. Знакопеременный ряд (с членами разных знаков)



называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных значений его членов:



Знакопеременный сходящийся ряд (1) называется условно сходящимся, если ряд (2) расходится.

Всякий абсолютно сходящийся ряд, есть ряд сходящийся.
Признак Лейбница.

Знакочередующийся ряд ,

сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е., если

и

При этом сумма ряда положительна и не превосходит первого члена.

Пример. Исследовать на сходимость:

1) ; 2) ; 3) ; 4)
1) Члены данного знакочередующегося ряда убывают по абсолютному значению, стремясь к нулю:

и

Поэтому, согласно признаку Лейбница, данный ряд сходится. Чтобы установить, сходится ли абсолютно или условно, исследуем ряд с положительными членами , составленный из абсолютных значений членов данного ряда. Применим предельный признак сравнения. Рядом сравнения к ряду является расходящийся гармонический ряд (т.к. )

Следовательно, ряд из абсолютных значений членов ряда расходится, а значит, исходный ряд сходится условно.
2) Заменим члены данного знакопеременного ряда, где - любое число, их абсолютными значениями и исследуем полученный ряд с положительными членами.

Сравним его с геометрической бесконечно убывающей прогрессией , которая является сходящимся рядом. Каждый член полученного ряда не превосходит соответствующего члена геометрической прогрессии.



Поэтому согласно признаку сравнения ряд с положительными членами также сходится, а заданный знакопеременный ряд сходится абсолютно.
3) Члены данного знакочередующегося ряда убывают по абсолютному значению, стремясь к нулю:

,

Поэтому согласно признаку Лейбница, он сходится. Ряд также сходится согласно признаку Даламбера:


Следовательно, данный ряд абсолютно сходится.

4) Для данного знакопеременного ряда не выполняется необходимое условие сходимости:

- не существует.

Следовательно, ряд расходится.
Задачи для решения.
В задачах 99-128 выяснить, сходится ли абсолютно, условно или расходится ряд:

99)

100)

101)

102)

103)

104)

105)

106)

107)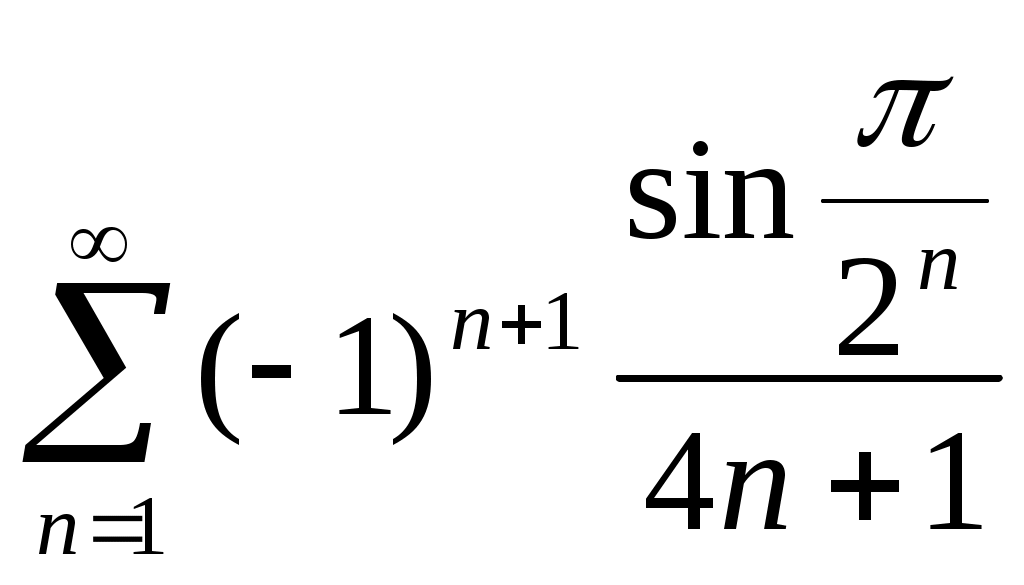

108)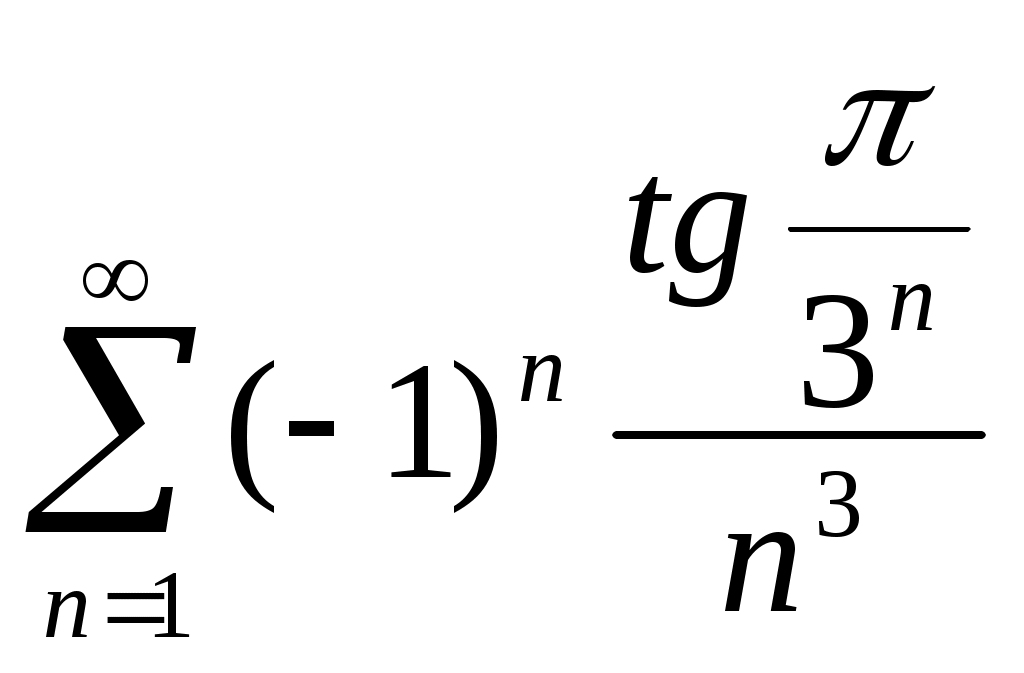

109)

110)

111)

112)

113)

114)

115)

116)

117)

118)

119)

120)

121)

122)

123)

124)

125)

126)

127)

128)