Шпоры по дисциплине Высшая математика. 1. Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла
 Скачать 1 Mb. Скачать 1 Mb.
|
|
1.Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла. Если существует конечный предел  интегральных сумм интегральных сумм 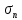 , когда диаметр , когда диаметр  разбиения стремится к 0, и этот предел не зависит: а) разбиения стремится к 0, и этот предел не зависит: а)от выбора разбиения и б)выбора точек ξi на частичных промежутках, то это предел и называется определенным интегралом от функции f про промежутку [a;b] и обозначается  , при этом функция f называется интегрируемой на промежутке [a;b]. , при этом функция f называется интегрируемой на промежутке [a;b].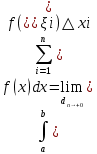 Геометрический смысл.  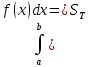 . .Интеграл по промежутку от неотрицательной на этом промежутке функции дает площадь соответствующей криволинейной трапеции, что по существу является определением площади криволинейной трапеции. Необходимое и достаточное условие интегрируемости функции вытекает из общего необходимого и достаточного условия единственности разделяющего числа. Напомним, что если числовое множество У расположено справа от числового множества , то для единственности Х числа, разделяющего Х и У , необходимо и достаточно выполнение условия 2.Основные свойства определенного интеграла. В дальнейшем будем считать рассматриваемые функции интегрируемыми на соответствующих промежутках. 1.Интеграл от единичной функции выражает длину отрезка [a;b]:  Кроме этого, по определению: Кроме этого, по определению:  , , 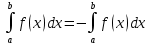 2. Линейность:  3.Аддитивность:  (интеграл по промежутку равен сумме интегралов по составляющим промежуткам [a;b]=[a;c]ᴗ[c;b] (интеграл по промежутку равен сумме интегралов по составляющим промежуткам [a;b]=[a;c]ᴗ[c;b] 4.Монотонность: если f(x)  g(x) для всех х g(x) для всех х ,a ,a b , то b , то  . . 5. Теорема о среднем: если функция непрерывна на [a;b], то на отрезке существует точка С такая, что 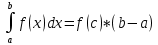 Геометрический смысл теоремы о среднем: если f(x)-нечётная функция, то 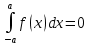 если f(x)-чётная функция, то 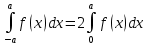 =2 =2 3 Теорема о среднем Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка e, a < e < b, в которой производная функция f(x) равная нулю, f¢(e) = 0. Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки. Ср знач ф-ии на отрезке Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка e a < e < b, такая, что  . .Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке. Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа. Отношение 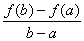 равно угловому коэффициенту секущей АВ. равно угловому коэффициенту секущей АВ.4. Интегралы с переменным верхним пределом. Пусть функция f(х) интегрируема на отрезке [a,b]. Для каждого x∈[a, b ] рассмотрим интеграл 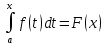 – функцию переменного верхнего предела. Оказывается, если f(x) интегрируема, то F(х) непрерывна; более того, имеет место теорема о дифференцировании определенного интеграла по переменному верхнему пределу: в каждой точке x∈(a, b), где f (x) непрерывна, функция F (x) является дифференцируемой, причем в этом случае производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, вычисленной на этом переменном верхнем пределе: – функцию переменного верхнего предела. Оказывается, если f(x) интегрируема, то F(х) непрерывна; более того, имеет место теорема о дифференцировании определенного интеграла по переменному верхнему пределу: в каждой точке x∈(a, b), где f (x) непрерывна, функция F (x) является дифференцируемой, причем в этом случае производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, вычисленной на этом переменном верхнем пределе: 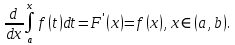 Пример:  5.Формула Ньютона-Лейбница. Пусть  – произвольная первообразная для непрерывной функции – произвольная первообразная для непрерывной функции  т. е. т. е.  Тогда Тогда  и и  – две первообразные для функции. Поэтому они различаются, разве лишь, на постоянную: – две первообразные для функции. Поэтому они различаются, разве лишь, на постоянную:  откуда, полагая откуда, полагая  , находим , находим 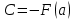 затем, принимая затем, принимая 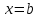 , получаем одну из основных формул интегрального исчисления – формулу Ньютона – Лейбница: , получаем одну из основных формул интегрального исчисления – формулу Ньютона – Лейбница: Где  – произвольная первообразная для – произвольная первообразная для 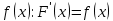 , a , a  - двойная подстановка. - двойная подстановка. Пример:  . .6.Замена переменной в определенном интеграле.  для определённого:  Функция y = f(x) называется четной, если для любого x из области определения функции выполняется равенство f(-x) = f(x). Функция y = f(x) называется нечетной, если для любого x из области определения функции выполняется равенство f(-x) = - f(x). Интегрирование четных и нечетных функций в симметричных пределах. Пусть f(x) непрерывна на отрезке[-a;a], т.е. на отрезке симметричном относительно начала координат. Тогда интеграл 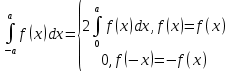 Доказательство: разобьем отрезок [-а;а] точкой 0, тогда по свойству аддитивности имеем  7. Вычисление площадей плоских фигур в полярной системе координат. Примеры. 1)В полярных координатах  ,y= ,y= : S= : S=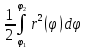 , если криволинейный сектор ограничен лучами , если криволинейный сектор ограничен лучами 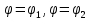 и кривой и кривой 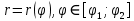 . . 2) S=  , если фигура ограничена лучами , если фигура ограничена лучами 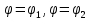 и кривыми и кривыми 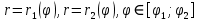 . .Пример: Найти площадь фигуры D, ограниченной одной из сторон аркой циклоиды 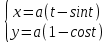 и осью абсцисс. Решение: одна арка образуется, когда параметр t изменяется например от 0 до 2π. Откуда: и осью абсцисс. Решение: одна арка образуется, когда параметр t изменяется например от 0 до 2π. Откуда:   8.Длина дуги кривой. Примеры. Под длиной s дуги кривой понимают предел вписанных в эту дугу длин ломаных, когда наибольшая из длин звеньев ломаных стремится к нулю. 1)Если рассматриваемая кривая L задана параметрически, то есть L: 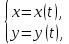 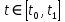 и является гладкой, то есть функции x(t), y(t) непрерывно дифференцируемы и их производные одновременно в нуль не обращаются, то выражение для дифференциала дуги можно уточнить: и является гладкой, то есть функции x(t), y(t) непрерывно дифференцируемы и их производные одновременно в нуль не обращаются, то выражение для дифференциала дуги можно уточнить:  . Получаем формулу для длины кривой: . Получаем формулу для длины кривой:  , ,  . . Пример: Есть L: 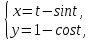 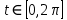 . .Решение: 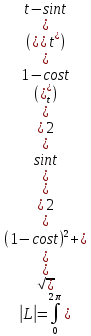 . .2)Если кривая L задана явно как график функции y=y(x),  , то формула для вычисления длины дуги упрощается (здесь t=x): , то формула для вычисления длины дуги упрощается (здесь t=x): 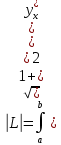 Пример: Найти длину дуги кривой L:= Пример: Найти длину дуги кривой L:=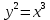 ,отсекаемую прямой х=1. (при вычислении 2 впереди - удвоение полученного результата, т.к. дуга лежит в 1 и 4 четвертях) ,отсекаемую прямой х=1. (при вычислении 2 впереди - удвоение полученного результата, т.к. дуга лежит в 1 и 4 четвертях)Откуда: |L|=2 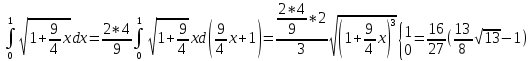 3)Аналогично можно рассмотреть выражение для нахождения дуги в полярных координатах, если в качестве t принять полярный угол ϕ. Тут r=r(ϕ) ,  : :  . .9. Вычисление объемов тел вращения. Примеры. Предположим, что тело G получено вращением фигуры, ограниченной линиями: y =f (x) ≥0, y =0, х =a, x=b, вокруг оси Ox. Тогда S(х) =πy2(x) – площадь круга и объем VG=Vxвыражается формулой  Аналогично  объем тела вращения вокруг оси Оу фигуры, ограниченной линиями: x=x( у) ≥0, x=0, y =c, y =d. объем тела вращения вокруг оси Оу фигуры, ограниченной линиями: x=x( у) ≥0, x=0, y =c, y =d.Пример. Найти объем тела, образованного вращением дуги параболы 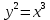 , отсекаемой , отсекаемой прямой x =1  Решение: 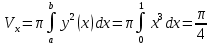 10. Вычисление работы  силового поля силового поля  при перемещении материальной точки при перемещении материальной точки  вдоль кривой L от точки А до точки В. вдоль кривой L от точки А до точки В.11. Несобственные интегралы по бесконечному промежутку. Примеры Понятие определенного интеграла было введено для конечного промежутка или отрезка, и непрерывной функции. Понятие определенного интеграла распространяется и на случай, когда промежуток бесконечен, или функция неограниченна в некоторой точке интервала. Такие интегралы называются несобственными. Несобственный интеграл 1 рода или по бесконечному промежутку. Пусть функция f(x) определена и непрерывна на промежутке [а;+∞), и интегрируема на любом конечном отрезке [а;b], то есть интеграл  Тогда несобственный интеграл первого рода называется конечным или бесконечным пределом Тогда несобственный интеграл первого рода называется конечным или бесконечным пределом  . Несобственный интеграл называется сходящимся, если существует конечный предел, и расходящимся, если предел равен +∞ или не существует. Аналогично определяются следующие несобственные интегралы 1 рода: . Несобственный интеграл называется сходящимся, если существует конечный предел, и расходящимся, если предел равен +∞ или не существует. Аналогично определяются следующие несобственные интегралы 1 рода:  ; ;  . .Пример:1)  2) 2) . .Пусть функция f(x) определена и непрерывна в (a;+∞) таким образом, что существует первообразная F(x) и на основании формулы Ньютона-Лейбница имеем  , следовательно несобственный интеграл существует тогда и только тогда, когда существует предел , следовательно несобственный интеграл существует тогда и только тогда, когда существует предел  . Возьмем интеграл: . Возьмем интеграл: Пример: Пример: 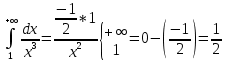 . .Теорема 1. Признак сравнения.(непредельный) Пусть функции f(x) и g(x) опеределены и непрерывны на отрезке [а;+∞) и связаны соотношением: f(x)≥g(x),тогда из сходимости интегралa  сходится интеграл сходится интеграл 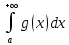 . Из расходимости интеграла . Из расходимости интеграла 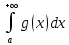 расходится расходится  . .Теорема 2. Признак сравнения. (предельный)Пусть функции f(x) и g(x) определены и непрерывны на промежутке (а;+∞) ,и существует 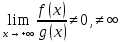 , то несобственные интегралы , то несобственные интегралы  ведут себя одинаково(либо сходятся, либо расходятся). ведут себя одинаково(либо сходятся, либо расходятся).12. Несобственные интегралы от неограниченных функций. Пример. Несобственные интегралы 2 рода или от неограниченных функций. Пусть f(x) определена на отрезке [a;b),и в точке имеет разрыв второго рода, причем на любом промежутке [a;c] содержащем отрезок [a;b). Тогда несобственный интеграл 2 рода называется  . Если предел существует и конечен, то интеграл – сходящийся, в противном случае определяется несобственный интеграл 2 рода: . Если предел существует и конечен, то интеграл – сходящийся, в противном случае определяется несобственный интеграл 2 рода:  . Если функция терпит разрыв во внутренней точке отрезка [a;b), то несобственный интеграл 2 рода определяется формулой: . Если функция терпит разрыв во внутренней точке отрезка [a;b), то несобственный интеграл 2 рода определяется формулой:  И для сходимости необходимо, чтобы сходились оба интеграла. Пусть функция определена на промежутке (a;b) и интегрируема на любом отрезке, содержащемся в (a;b), тогда НИ 2 рода существует, если существует предел И для сходимости необходимо, чтобы сходились оба интеграла. Пусть функция определена на промежутке (a;b) и интегрируема на любом отрезке, содержащемся в (a;b), тогда НИ 2 рода существует, если существует предел  . Пример . Пример  - расходящийся. - расходящийся.Теорема 3. Признак сравнения. Пусть f(x) и g(x) определены и непрерывны на промежутке [a b) и в точке b имеют разрыв 2 рода f(x)≥g(x). Из сходимости интеграла  сходится сходится 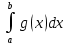 . Из расходимости . Из расходимости 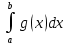 расходится расходится  . .Теорема 4. Признак сравнения. Если f(x) и g(x) определены и непрерывны на промежутке (a;b),и в точке b имеют разрыв 2 рода, то существует предел отношения  , то некоторые интегралы ведут себя одинаково. , то некоторые интегралы ведут себя одинаково.Геометрически НИ 1 рода представляет собой площадь криволинейной трапеции, а НИ 2 рода представляет собой бесконечно высокую криволинейную трапецию. |
