Шпоры по дисциплине Высшая математика. 1. Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла
 Скачать 1 Mb. Скачать 1 Mb.
|
|
23.Двойной интеграл. Основные понятия и определения Рассмотрим в плоскости 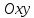 квадрируемую– измеримую(т. е. имеющую площадь) фигуру(область) квадрируемую– измеримую(т. е. имеющую площадь) фигуру(область) 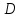 , на которой определена некоторая функция , на которой определена некоторая функция 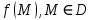 . Осуществим далее n-разбиение области D на n пересекающихся, разве лишь, по линиям квадрируемых частичных областей . Осуществим далее n-разбиение области D на n пересекающихся, разве лишь, по линиям квадрируемых частичных областей 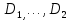 так, чтобы: так, чтобы: 1) 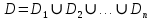 2) площадь 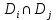 равна нулю равна нулю 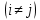 и составим сумму и составим сумму 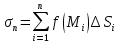 где где 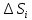 – площадь – площадь 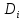 ; ; 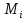 – произвольная точка, принадлежащая – произвольная точка, принадлежащая 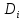 . . Сумму вида 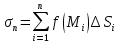 будем называть интегральной суммой для функции f и фигуры D. будем называть интегральной суммой для функции f и фигуры D. 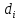 (диаметр)– наибольшее расстояние между точками области (диаметр)– наибольшее расстояние между точками области 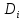 ,наибольший из частичных диаметров– диаметр разбиения ( ,наибольший из частичных диаметров– диаметр разбиения ( 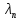 ): ): 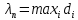 Если существует конечный предел интегральных cумм 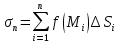 при диаметре разбиения, стремящемся к нулю, независимо от способа разбиения области D на части и от выбора точек при диаметре разбиения, стремящемся к нулю, независимо от способа разбиения области D на части и от выбора точек 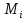 в частичных областях, то этот предел называется двойным интегралом от функции f по области D и обозначается в частичных областях, то этот предел называется двойным интегралом от функции f по области D и обозначается 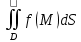 . .Таким образом, 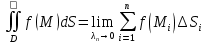 Функция 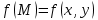 в этом случае называется интегрируемой в области D. в этом случае называется интегрируемой в области D. Как и в случае определенного интеграла имеют место следующие условия интегрируемости: необходимое: если функция интегрируема, то она ограничена, и достаточное: если функция непрерывна, то она интегрируема. 23. Двойной интеграл и его геометрический и физический смыслы. Геометрический смысл двойного интеграла: Объем V цилиндрического тела, ограниченного сверху непрерывной поверхностью z=f(x;y)≥0, снизу- замкнутой областью D в плоскости Oxy и с боков- цилиндрической поверхностью с направляющей- границей области D и образующей, параллельной оси Oz, выражается интегралом 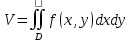 . .Физический смысл двойного интеграла: Масса mD материальной пластины D с поверхностной плотностью 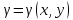 в точке M(x,y) рассчитывается по формуле: в точке M(x,y) рассчитывается по формуле: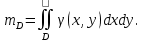 23.Основные свойства двойного интеграла:( считаем рассматриваемые функции интегрируемыми) Интеграл от единичной функции выражает площадь области интегрирования: 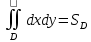 - площадь фигуры D - площадь фигуры DЛинейность: 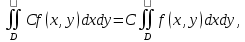 C=const C=const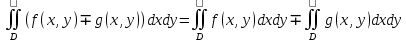 Аддитивность: 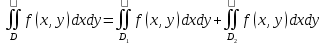 Монотонность: если в области D имеет место неравенство 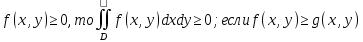 для любых (x,y) для любых (x,y)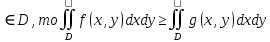 . В частности,для непрерывной на D функции f имеет место оценка: . В частности,для непрерывной на D функции f имеет место оценка: 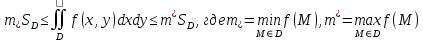 Теорема о среднем. Если функция f непрерывна в области D, то в области D найдётся точка 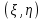 такая,что такая,что 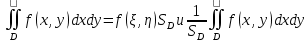 – среднее значение функции f в области D – среднее значение функции f в области D24. Тройной интеграл. Основные понятия. . 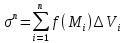 , , 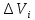 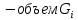 ; ; 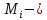 произвольная точка, принадлежащая Gi. произвольная точка, принадлежащая Gi.Символом di обозначим диаметр Gi- найбольшее расстояние между точками области Gi, наибольший из частичных диаметров – диаметром разбиения – символом λn:λn= 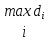 . .Если теперь существует конечный предел интегральных сумм n σ при диаметре разбиения, стремящемся к нулю, независимо от способа разбиения области G на части и от выбора точек i M в частичных областях, то этот предел называется тройным интегралом от функции f по области G и обозначается 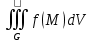 . .Как и в случае определенного интеграла имеют место следующие условия интегрируемости: необходимое: если функция интегрируема, то она ограничена, и достаточное: если функция непрерывна, то она интегрируема. Тройной интеграл в декартовых координатах и его свойства. Объем: 1) 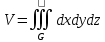 2) декартовые координаты 2) декартовые координаты 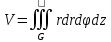 25. Криволинейные интегралы первого рода, их свойства и вычисление. Предположим, что на плоскости Oxy задана гладкая кривая L. Тогда дл любой ее дуги определено понятие lL*-длины дуги L*. Произвольным образом осуществляем n-разбиение кривой L на n частей. Пусть далее на кривой L задана некоторая скалярная функция F(x,y), (x,y) 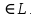 На каждой из полученных дуг Li длиной На каждой из полученных дуг Li длиной 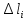 произвольно выберем точку произвольно выберем точку 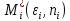 и составим интегральную сумму: и составим интегральную сумму: 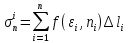 . dn- наибольшая из длин частичных дуг Li. Если при n→+∞, dn→0 существует конечный предел интегральных сумм и это т предел не зависит от способа разбиения кривой на части и от выбора точек, то такой предел –криволинейный предел первого рода. Свойства: . dn- наибольшая из длин частичных дуг Li. Если при n→+∞, dn→0 существует конечный предел интегральных сумм и это т предел не зависит от способа разбиения кривой на части и от выбора точек, то такой предел –криволинейный предел первого рода. Свойства:Линейность: 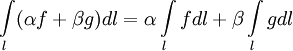 Аддитивность: если в одной точке, то 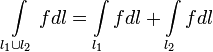 Монотонность: если на , то 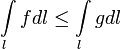 Очевидно, что: 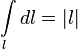 . .5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: 6. Криволинейный интеграл первого рода не зависит от параметризации кривой. Вычисление: Рассмотрим в пространстве гладкую параметризованную кривую L: 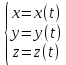 , , 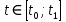 Тогда вычисление криволинейных интегралов сводится к нахождению определенных интегралов: 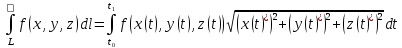 В случае КРИ-1 на плоскости, когда кривая задается с помощью непрерывно дифф.функции y=y(x) и xє[a;b] 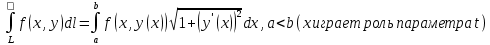 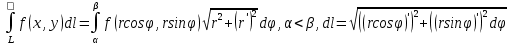 26.Криволинейные интегралы 2 рода, их свойства и вычисления. Связь между КРИ-1 и КРИ-2 Если при n→+∞, dn→0 существует конечный предел интегральных сумм и это т предел не зависит от способа разбиения кривой на части и от выбора точек, то такой предел –криволинейный предел первого рода. Свойства: Вычисление: Рассмотрим в пространстве гладкую параметризованную кривую L: 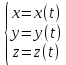 , , 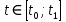 Тогда вычисление криволинейных интегралов сводится к нахождению определенных интегралов: 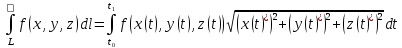 25. Приложения КРИ 1-го рода (длина кривой, площадь цилиндрической поверхности, масса кривой, статические моменты). 1. Вычисление длины li дуги L кривой: 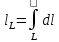 . 2. Вычисление массы материальной кривой L с линейной плотностью ρ(x,y,z), (x,y,z) . 2. Вычисление массы материальной кривой L с линейной плотностью ρ(x,y,z), (x,y,z)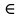 L: L: 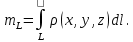 3. Для простоты ограничимся рассмотрением кривой L в плоскости Oxy. Вычисление статических моментов Mx, My материальной кривой L относительно координатных осей Ox и Oy соответственно: 3. Для простоты ограничимся рассмотрением кривой L в плоскости Oxy. Вычисление статических моментов Mx, My материальной кривой L относительно координатных осей Ox и Oy соответственно: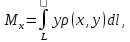 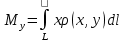 , , координат центра тяжести (центра масс) кривой L: 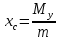 , , 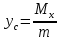 , ,а также моментов инерции кривой L относительно осей Ox и Oy и начала координат соответственно: 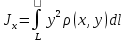 , , 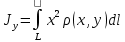 , , 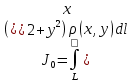 , где ρ(x,y) – линейная плотность распределения центра тяжести однородного дуги циклоиды: , где ρ(x,y) – линейная плотность распределения центра тяжести однородного дуги циклоиды: 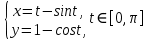 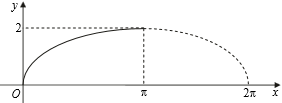 площадь цилиндрической поверхности: 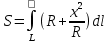 26. Приложения КРИ 2-го рода (площадь плоской фигуры, работа переменной силы). 1. Вычисление работы  силового поля силового поля  при перемещении материальной точки при перемещении материальной точки 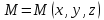 вдоль кривой L от точки А до точки В. вдоль кривой L от точки А до точки В.2. Вычисление площади плоской фигуры на основе теоремы Грина. Предположим, что в плоскости Oxy имеется односвязная область D (это значит, что в ней нет «дыр»), ограниченная кривой L. Формула Грина. Если функции P(x,y) и Q(x,y) непрерывны вместе со своими частными производными 1го порядка в односвязной области D, то имеет место формула 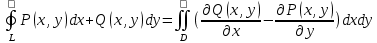 где L – граница области D и интегрирование ведется в полож-м направл. Из ф- лы Грина вытекает, что площадь где L – граница области D и интегрирование ведется в полож-м направл. Из ф- лы Грина вытекает, что площадь 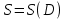 области D может быть рассчитана при помощи криволин-го интеграла 2го рода: области D может быть рассчитана при помощи криволин-го интеграла 2го рода: 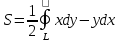 27. Условия независимости КРИ-2 от пути интегрирования. Потенциал. Условия независимости криволинейного интеграла (второго рода) от формы пути интегрирования Пусть функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны в некоторой области D пространства XYZ. Будем рассматривать в этой области только кусочно-гладкие кривые. Возьмем в области D две произвольные точки А и В. Их можно соединять различными кривыми, лежащими в области D. По каждой из этих кривых интеграл 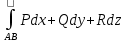 имеет, вообще говоря, свое значение. имеет, вообще говоря, свое значение.Теорема. Для того, чтобы криволинейный интеграл 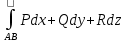 , где P(x, y, z), Q(x, y, z) и R(x, y, z) – функции, непрерывные в области D, в этой области не зависел от формы пути, необходимо и достаточно, чтобы выражение , где P(x, y, z), Q(x, y, z) и R(x, y, z) – функции, непрерывные в области D, в этой области не зависел от формы пути, необходимо и достаточно, чтобы выражение 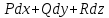 было полным дифференциалом некоторой функции (в области D). было полным дифференциалом некоторой функции (в области D).Теорема. Если функции P(x, y, z), Q(x, y, z) и R(x, y, z) в области D 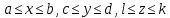 имеют непрерывные частные производные первого порядка, то, для того чтобы выражение имеют непрерывные частные производные первого порядка, то, для того чтобы выражение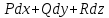 в этой области было полным дифференциалом некоторой функции, необходимым и достаточным является выполнение условий: в этой области было полным дифференциалом некоторой функции, необходимым и достаточным является выполнение условий: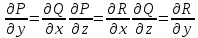 в каждой точке области D. 27. Формула Грина и её физический смысл 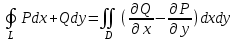 Нахождение циркуляции плоского векторного поля, в физике – для решения двумерных потоковых интегралов. Пример: Вычислить циркуляцию плоского векторного поля 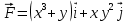 вдоль замкнутого контура L:y=0, вдоль замкнутого контура L:y=0, 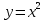 ,x=1. Обход такой, что область слева. Решение: Р= ,x=1. Обход такой, что область слева. Решение: Р=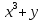 Q=xy^2, то частная производная по Р=1,по Q=y^2. Q=xy^2, то частная производная по Р=1,по Q=y^2. 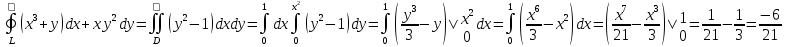 28.   2  9. 9.  30. Основные понятия теории поля. Потенциальные векторные поля. Циркуляция. Векторное поле F называется потенциальным (безвихревым) в области D, если криволинейный интеграл 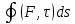 (циркуляция векторного поля) равен нулю по любой замкнутой кусочно- гладкой кривой L, расположенной в области D (здесь – 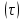 единичный единичныйвектор касательной к кривой L). Необходимым и достаточным условием потенциальности векторного поля в поверхностно-односвязной области D является равенство нулю его ротора во всех точках этой области: rotF =0 Циркуляция векторного поля Пусть векторное поле задано вектором F = P(x, y, z)i + Q(x, y, z) j + R(x, y, z)k, (x, y, z)∈G, причем функции P(x, y, z),Q(x, y, z), R(x, y, z) непрерывны в области G. Пусть L – гладкая или кусочно-гладкая замкнутая ориентированная кривая, т. е. на ней выбрано определенное направление. Циркуляцией векторного поля F(М) вдоль замкнутой ориентированной кривой L называется криволинейный интеграл второго рода:  = =  31.Ротор и дивергенция векторного поля, их физический смысл и вычисление: Дивергенция div  (M) векторного поля в точке М называется предел отношения потока поля через замкнутую поверхность (M) векторного поля в точке М называется предел отношения потока поля через замкнутую поверхность  окружающую точку М,к объёму тела,ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку М: окружающую точку М,к объёму тела,ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку М: В случае, когда компоненты P=P(M), Q=Q(M), R=R(M) векторного поля  непрерывны по совокупности переменных вместе со своими частными производными, дивергенция векторного поля в точке М определяется соотношением: непрерывны по совокупности переменных вместе со своими частными производными, дивергенция векторного поля в точке М определяется соотношением:   div  - дивергенция есть скалярное произведение оператора Гамильтона на вектор - дивергенция есть скалярное произведение оператора Гамильтона на вектор  Дивергенция характеризует мощность источника в случае div  , или стока в случае div , или стока в случае div находящегося в точке М. находящегося в точке М.Ротором (вихрем) векторного поля  , (x,y,z) , (x,y,z) G, где функции P(x,y,z) , Q(x,y,z) , R(x,y,z) и их производные первого порядка по координатам непрерывны в области G, называется вектором G, где функции P(x,y,z) , Q(x,y,z) , R(x,y,z) и их производные первого порядка по координатам непрерывны в области G, называется вектором  определяемый равенством: определяемый равенством:   Формальный определитель можно раскрывать только по первой строке |
