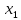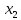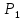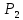Шпоры по дисциплине Высшая математика. 1. Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла
 Скачать 1 Mb. Скачать 1 Mb.
|
|
46. Схема Бернулли. Предельные теоремы: Пуассона,локальная и интегральная теоремы Муавра-Лапласа: Пусть проводится n независимых испытаний, в каждом из которых возможно только два исхода: А-успех и  неуспех,причем вероятность наступления успеха в каждом испытании постоянна и равна р. Такая последовательность испытаний называется схемой Бернулли. неуспех,причем вероятность наступления успеха в каждом испытании постоянна и равна р. Такая последовательность испытаний называется схемой Бернулли.В схеме Бернулли вероятность 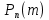 наступления m успехов в n независимых испытаниях- вероятность того,что в этих испытаниях событие А наступит ровно m раз, вычисляется по формуле Бернулли: наступления m успехов в n независимых испытаниях- вероятность того,что в этих испытаниях событие А наступит ровно m раз, вычисляется по формуле Бернулли: 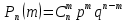 , где , где 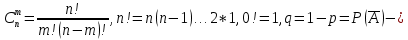 вероятность неуспеха в одном испытании вероятность неуспеха в одном испытанииЕсли в схеме Бернулли вероятность р появления события А в каждом из n независимых крайне мала, а число испытаний n достаточно велико, то вероятность вычисляется приближённо по формуле Пуассона: 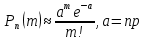 . Формулу Пуассона применяют, когда событие А является редким, но количество испытаний n велико и среднее число успехов a=np незначительно (а . Формулу Пуассона применяют, когда событие А является редким, но количество испытаний n велико и среднее число успехов a=np незначительно (а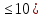 Если в схеме Бернулли вероятность р появления события А в каждом из n независимых испытаний существенно отличается от 0 и 1 (близко ½), а число испытаний n достаточно велико, то для вычисления вероятности применяют приближённую локальную формулу Муавра-Лапласа: 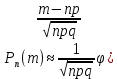 ) )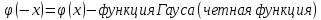 Если в схеме Бернулли вероятность р существенно отличается от 0 и 1, n достаточно велико, то вероятность 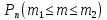 того,что в n независимых испытаниях событие А наступит не менее того,что в n независимых испытаниях событие А наступит не менее  раз, но не менее раз, но не менее 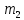 раз, вычисляется по интегральной формуле Муавра-Лапласа):ф(х)- нечетная,Лапласа раз, вычисляется по интегральной формуле Муавра-Лапласа):ф(х)- нечетная,Лапласа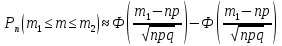 47. Функция распределения случайной величины и ее свойства. Определение случайной величины. Под случайной величиной будем понимать величину, которая в результате случайного эксперимента одно и только одно возможное значение, которое заранее неизвестно и зависит от случайных причин. Более строго под случайной величиной понимают действительно значную функцию ξ, определенную на множестве Ω элементарных событий и такую, что для любой системы В открытых интервалов, В  , существует , существует 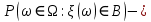 вероятность того, что случайная величина примет значение из В. вероятность того, что случайная величина примет значение из В.Таким образом для любой случайной величины определена функция :  – функция распределения. – функция распределения.Основные свойства функции распределения случайной величины: 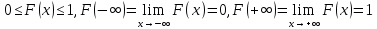 F(x)- неубывающая, непрерывная слева функция, то есть 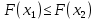 при при 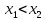 и и 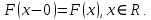 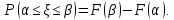 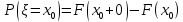 48.49. Дискретные случайные величины и способы их задания. Биноминальное, геометрическое и распределение Пуассона. Случайная величина называется дискретной, если множество ее возможных значений конечно или счётно ( т.е. если все ее значения можно занумеровать). Закон распределения ДСВ 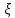 удобно задать в виде таблицы, называемой рядом распределения этой СВ: удобно задать в виде таблицы, называемой рядом распределения этой СВ:
Отметим, что 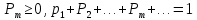 - условие контроля. - условие контроля.Отсюда получаем функцию распределения ДСВ: 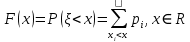 График функции распределения ДСВ имеет ступенчатый вид, причем функция распределения терпит разрывы в точках 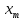 со скачками со скачками  , m=1,2,… , m=1,2,…Математическое ожидание дискретной СВ 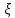 : :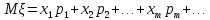 (предполагается,что ряд в правой части этого равенства абсолютно сходится) характеризует среднее значение СВ 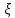 1)СВ 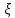 имеет биноминальное распределение с параметрами n и p, если она принимает значения 0,1,2,…,n с вероятностями: имеет биноминальное распределение с параметрами n и p, если она принимает значения 0,1,2,…,n с вероятностями: Биномиальный закон распределения имеет место в том случае, когда СВ 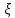 выражает число появлений события А(число успехов) при n независимых испытаниях в схеме Бернули. Математическое ожидание и дисперсия СВ выражает число появлений события А(число успехов) при n независимых испытаниях в схеме Бернули. Математическое ожидание и дисперсия СВ 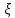 , распределённой по биномиальному закону,вычисляются по формулам: , распределённой по биномиальному закону,вычисляются по формулам: 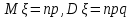 2) Дискретная СВ 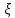 имеет распределение Пуассона с параметром а, если она принимает значения 0,1,2,…,n,… с вероятностями: имеет распределение Пуассона с параметром а, если она принимает значения 0,1,2,…,n,… с вероятностями: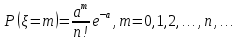 математическое ожидание и дисперсия СВ математическое ожидание и дисперсия СВ 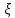 , распределённой по закону Пуассона, равны , распределённой по закону Пуассона, равны 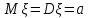 . Закон распределения Пуассона( закон редких явлений) является хорошим приближением для биномиального распределения при больших значениях n и малых p ( или 1-р) . Закон распределения Пуассона( закон редких явлений) является хорошим приближением для биномиального распределения при больших значениях n и малых p ( или 1-р)3) Геометри́ческое распределе́ние — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха». Пусть — бесконечная последовательность независимых случайных величин сраспределением Бернулли, то есть 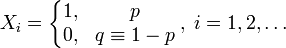 Построим случайную величину Функция вероятности случайной величины имеет вид:  50. Непрерывные случайные величины и способы их задания. Равномерное, показательное распределение. Случайная величина называется непрерывной (НСВ), если её функция распределения F(x)=P(ξ Функция p(x) называется плотностью распределения вероятностей НСВ ξ с функцией распределения F(x), если  откуда p(x)=F’(x) откуда p(x)=F’(x)Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность вероятности имеет вид:  , где Mξ = a; Dξ = σ2 . Вероятность попадания случайной величины в заданный интервал (α; β) вычисляется по формуле , где Mξ = a; Dξ = σ2 . Вероятность попадания случайной величины в заданный интервал (α; β) вычисляется по формуле 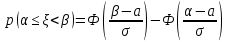 . .51. НСВ ξимеет равномерное распределение на отрезке [a,b], если её плотность распределения постоянна на этом отрезке, а вне его равна нулю: 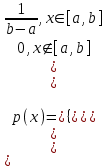 Распределение НСВ ξ называется показательным с параметром λ>0, если её плотность распределения имеет следующий вид:    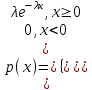 Функция показательного распределения 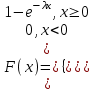 52. Распределение НСВ ξ называется показательным с параметром λ>0, если её плотность распределения имеет следующий вид:    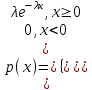 Функция показательного распределения 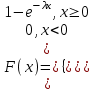 53. Нормальный закон распределения (распределения Гаусса)Трех сигм Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность вероятности имеет вид:  , где Mξ = a; Dξ = σ2 . Вероятность попадания случайной величины в заданный интервал (α; β) вычисляется по формуле , где Mξ = a; Dξ = σ2 . Вероятность попадания случайной величины в заданный интервал (α; β) вычисляется по формуле 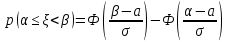 . В силу непрерывности СВ эта формула справедлива как со строгими, так и с нестрогими знаками неравенств. . В силу непрерывности СВ эта формула справедлива как со строгими, так и с нестрогими знаками неравенств.Вероятность отклонения случайной величины от математического ожидания на величину δ равна; 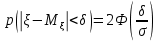 . Здесь . Здесь 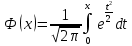 – функция Лапласа; Φ(−x) = −Φ(x) – функция нечетная; Φ(0) = 0 ; Φ(x ≥ 5) = 0,5. – функция Лапласа; Φ(−x) = −Φ(x) – функция нечетная; Φ(0) = 0 ; Φ(x ≥ 5) = 0,5.Правило «трех сигм» для нормального распределения. Если СВ ξ распределена нормально с параметрами a и σ, то попадание ее в интервал (a-3σ, a+3σ) является практически достоверным событием, и, стало быть, вероятность противоположного со- бытия ничтожно мала и на практике таким событием пренебрегают. 54. .Свойства плотности распределения случайной величины. Функция  называется плотностью распределения вероятностей непрерывной случайной величины ξ с функцией распределения называется плотностью распределения вероятностей непрерывной случайной величины ξ с функцией распределения  , если , если 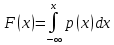 , откуда , откуда 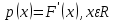 . .Основные свойства плотности распределения НСВ: 1. 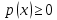 при всех при всех 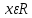 2. 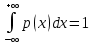 Геометрически это означает, что график плотности распределения лежит не ниже оси Ox и площадь под графиком плотности равна единице. 3. Вероятности попадания непрерывной случайной величины ξ в интервал, отрезок или полуинтервал с одними и теми же концами одинаковы и равны: 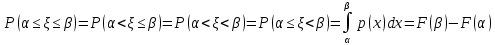 Геометрически вероятность 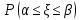 представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности, осью абсцисс и отрезками прямых представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности, осью абсцисс и отрезками прямых 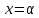 и и 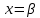 . .1) математическое ожидание M ξ характеризует среднее значение(центр рассеивания) СВ M ξ= 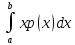 2) дисперсия Dξ = M(ξ2 )–( Mξ)2, которая характеризует величину (меру) рассеивания значений СВ около ее математического ожидания; 3) среднее квадратическое отклонение =D ξ которое (в отличие от дисперсии) имеет размерность СВ ξ Mξk– начальные моменты k-го порядка; M(ξ − Mξ)k– центральные моменты k-го порядка. 55. Графическое изображение статистических рядов Эмпирическая функция распределения. Гистограммой относительных частот для интервального ряда группированной выборки называют ступенчатую фигуру, составленную из прямоугольников, построенных на интервалах группировки так, что площадь каждого прямоугольника равна соответствующей данному интервалу относительной частоте. Площадь гистограммы относительных частот равна 1. При достаточно большом объеме выборки и достаточно малых интервалах группировки гистограмма относительных частот является статистической оценкой вида плотности распределения pξ(x). Полигоном частот группированной выборки называется ломаная с вершинами в точках 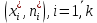 , а полигоном относительных частот- ломаная линия с вершинами в точках , а полигоном относительных частот- ломаная линия с вершинами в точках 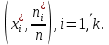 Если плотность распределения генеральной совокупности достаточно гладкая функция, то полигон относительных частот- более хорошее приближение плотности, чем гистограмма. Если плотность распределения генеральной совокупности достаточно гладкая функция, то полигон относительных частот- более хорошее приближение плотности, чем гистограмма.Эмпирической функцией распределения случайной величины ξ называется функция F*(x), определяющая для каждого значения x относительную частоту наблюдения значений, меньших x (ξ Эмпирическая функция распределения является случайной: для разных выборок она получается разной. Выборочным средним  называется среднее арифметическое элементов выборки: называется среднее арифметическое элементов выборки: 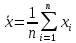 . Для группированной выборки: . Для группированной выборки: 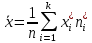 , где , где  середины интервалов группировки, середины интервалов группировки,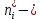 количество элементов выборки, попавших в i-тый интервал. количество элементов выборки, попавших в i-тый интервал.56. Интервальные оценки параметров распределения. Интервальные оценки параметров распределения Доверительной вероятностью, или надежностью, оценки называется вероятность γ, с которой выполняется неравенство 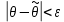 т.е т.е 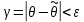 где θ – оцениваемый параметр, ε – точность оценки. где θ – оцениваемый параметр, ε – точность оценки.Доверительным интервалом для параметра θ ГС называется интервал (  который накрывает θ с вероятностью который накрывает θ с вероятностью(надежностью) γ. В практике важную роль играет длина доверительного интервала, причем чем меньше его длина, тем точнее оценка. Если длина доверительного интервала достаточно вели- ка, то оценка малопригодна для практики. Выбор доверительной вероятности определяется конкретными условиями. Обычно используются значения 0,90; 0,95; 0,99; 0,9973. Значение α = 1 – γ называется уровнем значимости. То́чечная оценка в математической статистике — это число, вычисляемое на основе наблюдений, предположительно близкое к оцениваемому параметру. Пусть х1,х2,хn выборка из генеральной совокупности, соответствующей случайной величине x с неизвестным математическим ожиданием Mx =q и известной дисперсией 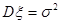 . .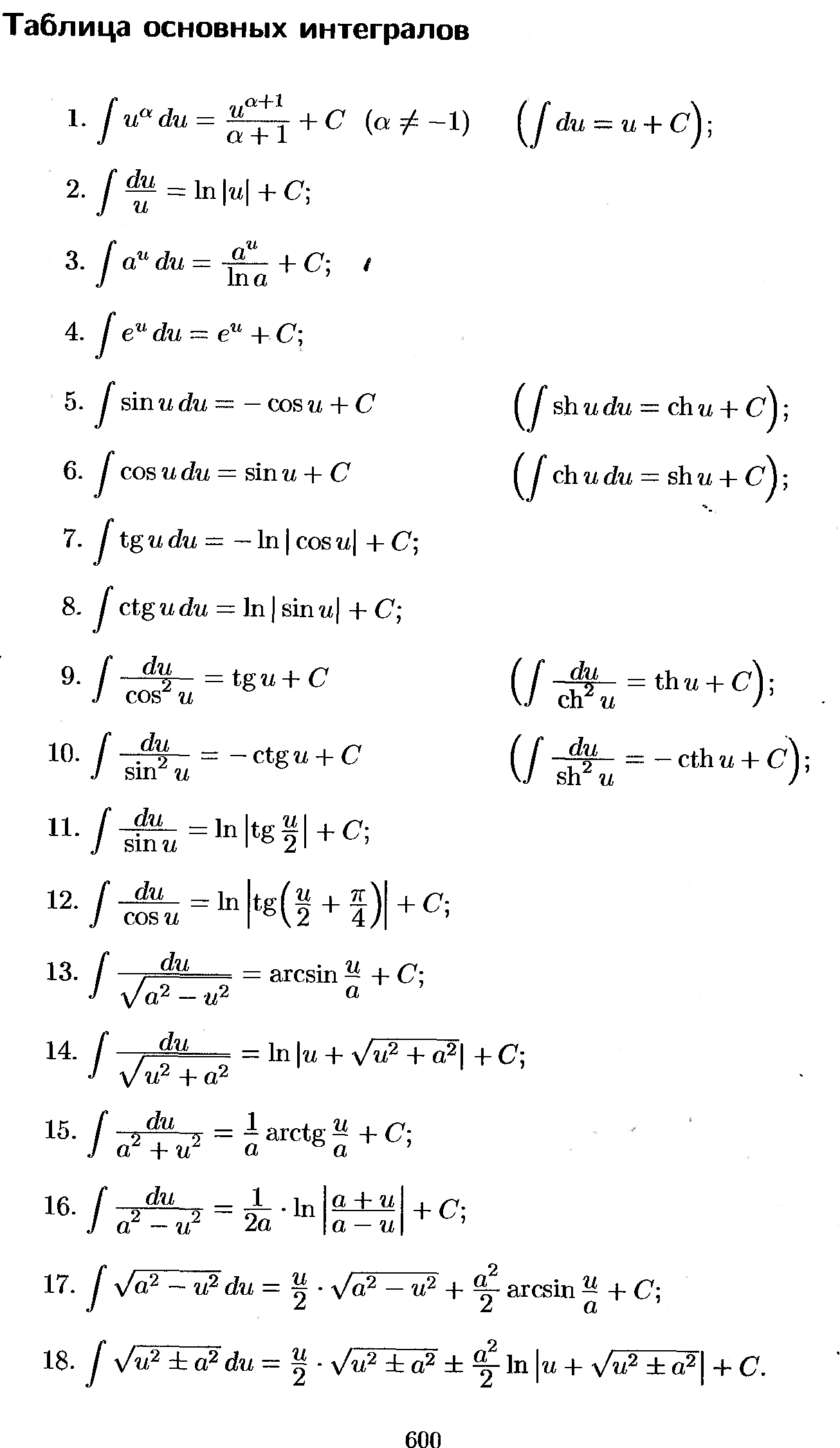 произв сложн ф-и, Производная обратной функции равна =произведен произодн этой ф-и по промеж аргуенту на производн промеж аргум по осн аргументу. о 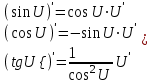 братной величине производной данной функции. братной величине производной данной функции.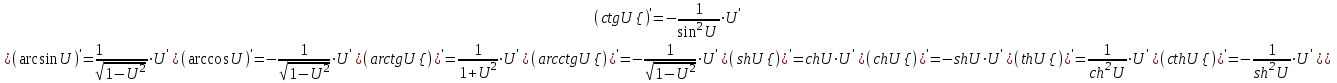 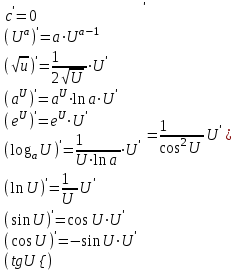 |