Математика Теория вероятностей. математика. Закон распределения имеет вид
 Скачать 89.42 Kb. Скачать 89.42 Kb.
|
|
Вариант 3 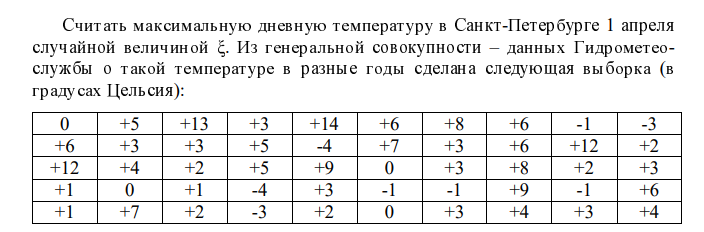  За 50 лет мы можем наблюдать 16 вариантов температуры, которая достигает своего максимума и выборочный закон распределения имеет вид:
Минимальная температура -4 градуса по цельсию Максимальная температура 14 градусов по цельсию n=50; k=16 Выборочное среднее: 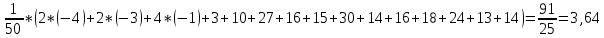 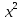 будет равен: будет равен: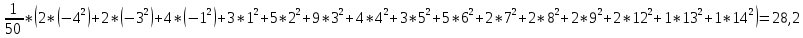 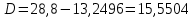 Выборочная дисперсия (исправленная): 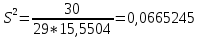 Известная дисперсия: D= 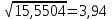 В таблице Лапласа мы видим, что 2Ф(1,65)=0,9, откуда ty=1,65 Далее зададим вероятность 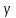 и по таблице Лапласа выберем такое и по таблице Лапласа выберем такое 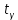 , , 2Ф( 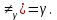 Тогда Тогда 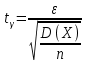 , откуда , откуда 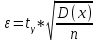 . Если такое . Если такое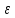 подставим в данную нам формулу, получим: подставим в данную нам формулу, получим: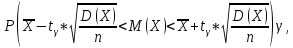 Если нам известна дисперсия случайной величины, то формула выше решает задачу. Если вместе с M(X) неизвестна и D(X), то из тех же опытных данных можно получить несмещенную и состоятельную оценку для дисперсии по формуле: 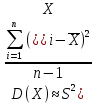 Тогда, первое уравнение имеет вид: 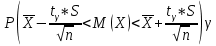 Теперь мы можем провести вычисления по полученным формулам и получить результат: 3,58 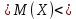 3,69 – это доверительный интервал. 3,69 – это доверительный интервал. Доверительный интервал для дисперсии: Вероятность выхода за нижнюю границу равна P(χ2n-1 < hH) = γ/2 =0.05 Для количества степеней свободы k=n-1=49, по таблице распределения χ2 находим: χ2(49;0.05) = 67.50481. Случайная ошибка дисперсии нижней границы: 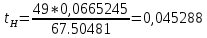 Вероятность выхода за верхнюю границу равна P(χ2n-1 ≥ hB) = 1 - P(χ2n-1 < hH) = 1 - 0.05 = 0.95: χ2(49;0.95) = 34.76425. Случайная ошибка дисперсии верхней границы: 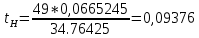 Таким образом, интервал ( 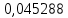 ; ; 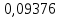 ) покрывает параметр S2 с надежностью α = 0.1 (γ=90%) ) покрывает параметр S2 с надежностью α = 0.1 (γ=90%) |
