Шпоры по дисциплине Высшая математика. 1. Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла
 Скачать 1 Mb. Скачать 1 Mb.
|
|
12. Обыкновенные дифференциальные уравнения. Основные понятия. Уравнение относительно неизвестной функции и ее производных принято называть дифференциальным. Порядок старшей производной, существенно входящей в данное ДУ, называется порядком этого ДУ. Если в определении ДУ искомая функция – функция одной переменной, то такое ДУ называется обыкновенным; если же функция нескольких переменных, и, стало быть, производные рассматриваются частные, то тогда говорят о ДУ с частными производными. Решением ( на множестве Х) ДУ n-го порядка называется произвольная n раз дифференцируемая функция y=y(x), x 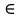 X, удовлетворяющая этому ДУ, т.е. при подстановке которой ДУ превращается в верное тождество ( на мн-ве Х). X, удовлетворяющая этому ДУ, т.е. при подстановке которой ДУ превращается в верное тождество ( на мн-ве Х).График решения ДУ наз. интегральной кривой этого ДУ. Начальная задача Коши. Рассмотрим ДУ n-го порядка, разрешенное относительно старшей производной, и мн-во X×D, где XcR, dcRn, на котором определена правая часть уравнения. Далее предположим, что в области X×D задана произвольная точка (x0, y00, y01, …, y0n-1) 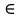 X×D. В области X×D рассматривается задача: среди решений ДУ найти такое, которое удовлетворяет следующим начальным условиям Коши: X×D. В области X×D рассматривается задача: среди решений ДУ найти такое, которое удовлетворяет следующим начальным условиям Коши: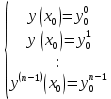 Ф-ция y=ϕ(x, C1, C2, …, Cn), x 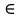 X, зависящая от независимой переменной х и n произвольных постоянных C1, …, Cn, называется общим решением ДУ, если она удовлетворяет слуддующим двум условиям: 1) при фиксированных значениях произвольных постоянных эта функция является решением (на множестве Х) этого ДУ; X, зависящая от независимой переменной х и n произвольных постоянных C1, …, Cn, называется общим решением ДУ, если она удовлетворяет слуддующим двум условиям: 1) при фиксированных значениях произвольных постоянных эта функция является решением (на множестве Х) этого ДУ;2) в области X×D эта функция решает любую задачу Коши, иначе говоря, для любой точки (x0, y00, y01,…, y0(n-1) в области X×D система: 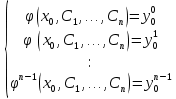 Решение, получающееся из общего при фиксированных значениях произвольных постоянных, принято называть частным. Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым. 13. Дифференциальные уравнения первого порядка. Геометрическая интерпретация. Теорема существования. 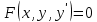 . .Общий вид ДУ первого порядка, разрешенного относительно производной: 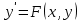 . . Начальная задача Коши: найти решение ДУ 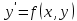 , удовлетв. начальному условию: , удовлетв. начальному условию: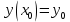 . .Вид общего решения: 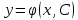 . .Геометрический смысл: Из геометрического смысла производной и ДУ получаем y'=f(x,y)=tgα-тангенс угла наклона касательной, проведенной к графику интегральной кривой y=y(x) в точке (x,y) для любой точки(x,y),в которой правая часть ДУ определена. Теорема существования и единственности решения. Предположим, что правая часть 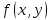 ДУ ДУ 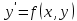 непрерывна в некоторой области непрерывна в некоторой области 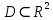 на плоскости по совокупности переменных, вместе с частной производной на плоскости по совокупности переменных, вместе с частной производной 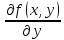 . Тогда в некоторой окрестности каждой точки . Тогда в некоторой окрестности каждой точки 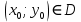 решение задачи Коши решение задачи Коши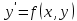 и и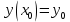 существует, и это решение единственно, т. е. в окрестности любой точки существует, и это решение единственно, т. е. в окрестности любой точки 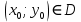 существует одна и только одна интегральная кривая ДУ существует одна и только одна интегральная кривая ДУ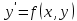 , проходящая через эту точку. , проходящая через эту точку.14.15.Дифференциальные уравнения с разделяющимися переменными и однородные. 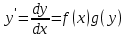 . ДУ с разделяющимися переменными интегрируем путем разделения переменных: . ДУ с разделяющимися переменными интегрируем путем разделения переменных: 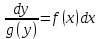 (переменные с x в одной части, а (переменные с x в одной части, апеременные с y – в другой) и последующим интегрированием: 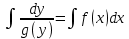 В результате получим либо y = ϕ(х,С) – общее решение, либо общий интеграл. Однородные ДУ: 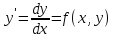 . Решаем подстановкой y = u x, . Решаем подстановкой y = u x,y′= xu′+ u. Приходим к ДУ с разделяющимися переменными u = u(x, c) ⇒y = xu(x, c) – общее решение (в некоторой области). 16.Линейные дифференциальные уравнения и способы их решения. ДУ вида 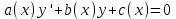 где а(х)≠0 где а(х)≠0ЛДУ интегрируется заменой y=uv y’=u’v+uv’ где u=u(x) новая неизвестная ф-я, v=v(x)вспомогательная ф-я Выполняя подстановку a(x)(u’v+uv’)+b(x)(uv)+c(x)=0 и вынося u за скобки получаем a(x)u’v+u(a(x)v’+c(x)=0. Выбирая вспомог. ф-ю так, чтобы выражение в скобках обратилось в ноль, приходим к системе ДУ с разделяющимися переменными: 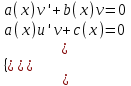 Уравнение Бернули. ДУ следующего вида a(x)y’+b(x)y+c(x)yn=0. 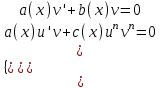 Из 1 уравнения системы находим вспомогательную ф-ю v, после подстановки которой во второе уравнение вновь получаем ДУ с разделяющимися переменными. Из 1 уравнения системы находим вспомогательную ф-ю v, после подстановки которой во второе уравнение вновь получаем ДУ с разделяющимися переменными. 17.Дифференциальные уравнения второго порядка, допускающие понижения порядка. 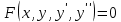 – общий вид ДУ второго порядка – общий вид ДУ второго порядка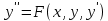 - общий вид ДУ второго порядка, разрешённого относительно старшей производной - общий вид ДУ второго порядка, разрешённого относительно старшей производной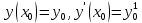 - начальные условия Коши - начальные условия Коши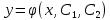 – вид общего решения – вид общего решенияСуществует два принципиально различных случая понижения порядка ДУ второго порядка: 1) ДУ второго порядка, в котором отсутствует неизвестная функция 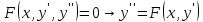 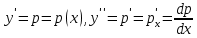 Получаем F(x,p, 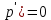 p= 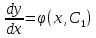 , dy= , dy=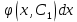 , y= , y=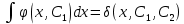 у= 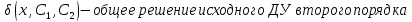 2) ДУ второго порядка, в котором отсутствует независимая переменная 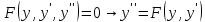 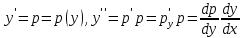 Получаем F(y,p, 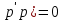 p= 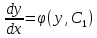 , , 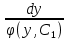 = =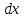 , x= , x=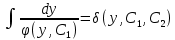 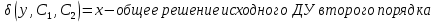 18. Дифференциальные уравнения второго порядка. Общие понятия. Примеры. Дифференциальное уравнение второго порядка можно записать в виде F( 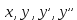 )=0 –общий вид. )=0 –общий вид.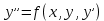 -общий вид дифференциального уравнения второго порядка, разрешенного относительно старшей степени. -общий вид дифференциального уравнения второго порядка, разрешенного относительно старшей степени.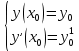 - начальные условия Коши - начальные условия Коши 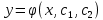 –вид общего решения. –вид общего решения.Существует два принципиально различных случая понижения порядка ДУ второго порядка- это, когда 1)отсутствует неизвестная функция у и 2)отсутствует независимая переменная х. Примеры: 1) 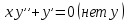 2) 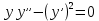 (нет х) (нет х)3) 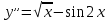 (тут (тут 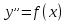 ) )19.Линейных дифференциальных уравнений второго порядка. Рассмотрим однородное ЛДУ L (у)=0 с постоянными коэффициентами, т. е. а1(х) ≡а1 , ..., an(x) ≡ an – действительные числа. Следуя идее Эйлера, ищем решение этого ЛДУ в виде , y=e xλ ,где λ – некоторое (в общем случае комплексное) число. Тогда y(k) = e x λ λ k .Подставляя выражения для искомой функции и ее производных в ЛДУ L(у )= 0, получаем: e x λ (λ n +a1 λ n-1+…+an-1 λ+an)=0, отсюда, сокращая на , ех λ ,приходим к характеристическому уравнению λn + a1 λ n-1+…+an-1 λ+an=0 для нахождения искомых чисел λ. Рассмотрим случай, когда характеристическое уравнение имеет n различных действительных корней λ 1,…, λп. В этом случае решения y1 = e x λ1,…,уп = e x λп образуют фундаментальную систему решений однородного ЛДУ, так как их вронскиан отличен от нуля, и поэтому общее решение однородного ЛДУ L (у)= 0 в случае различных корней характеристического уравнения имеет вид у= уо.о (x) = C1 e x λ1 + Cne λnx. 20. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Рассмотрим однородное ЛДУ L (у)=0 с постоянными коэффициентами, т. е. а1(х) ≡а1 , ..., an(x) ≡ an – действительные числа. Следуя идее Эйлера, ищем решение этого ЛДУ в виде , y=e xλ ,где λ – некоторое (в общем случае комплексное) число. Тогда y(k) = e x λ λ k .Подставляя выражения для искомой функции и ее производных в ЛДУ L(у )= 0, получаем: e x λ (λ n +a1 λ n-1+…+an-1 λ+an)=0, отсюда, сокращая на , ех λ ,приходим к характеристическому уравнению λn + a1 λ n-1+…+an-1 λ+an=0 для нахождения искомых чисел λ. 21. Метод Лагранжа вариации произвольных постоянных в теории дифференциальных уравнений. Рассмотрим его на примере ЛДУ второго порядка: y′′+ p(x) y′+ q(x) y = f (x). при условии, что известна фундаментальная система решений одно- родного ЛДУ ( y = y1(х), y = y2 (х)). Тогда частное решение неоднородного ЛДУ ищется в виде y = yн (x) = C1(x) y1(x) + C2 (x) y2 (x),  Подставляемy′′ + p(x) y′ + q(x) y = C1(х) y1′′(х) + p(x) y1′(х) + q(x) y1(х) + Подставляемy′′ + p(x) y′ + q(x) y = C1(х) y1′′(х) + p(x) y1′(х) + q(x) y1(х) +( ) + C2 (х) y2′′(х) + p(x) y2′ (х) + q(x) y2 (х) + C1′(х) y1′(х) + C2′ (х) y′2 (х) ≡ ≡ f (х). Для нахождения С1(х) и С2(х) получаем систему  определяем C1′(х) = a(x) и C2′(х) = b(x)и интегрируем. yн (x) = y1(x) ∫ a(x)dx + y2 (x) ∫b(x)dx и общее решение определяем C1′(х) = a(x) и C2′(х) = b(x)и интегрируем. yн (x) = y1(x) ∫ a(x)dx + y2 (x) ∫b(x)dx и общее решениеy = yо.о (x) + yн (x) неоднородного ЛДУ имеет вид y = C y1(х) +C2 y2 (х) + y1(x) ∫ a(x)dx + y2 (x) ∫b(x)dx. 22. Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью. Уравнение вида  (1), где p и q – постоянные: f (x) – определенная на некотором интервале функция, называется линейным неоднор-м дифура-м 2-го порядка с пост-ми коэфф-ми. Если f (x) ≡ 0 , то уравнение называется линейным однор. дифуром. (1), где p и q – постоянные: f (x) – определенная на некотором интервале функция, называется линейным неоднор-м дифура-м 2-го порядка с пост-ми коэфф-ми. Если f (x) ≡ 0 , то уравнение называется линейным однор. дифуром. Общее решение уравнения (1) есть сумма общего реш  соотв-го однор-го ур-я и частного решения y* исходного неоднородного уравнения, т. е. соотв-го однор-го ур-я и частного решения y* исходного неоднородного уравнения, т. е.  . Однор ур-е y′′ + yp ′ + qy = 0 явл частным случаем неоднор-го и для его решения составл-ся хар-е уравнение . Однор ур-е y′′ + yp ′ + qy = 0 явл частным случаем неоднор-го и для его решения составл-ся хар-е уравнение  . Решаем хар-е уравнение. Вид общего решения y(x)определяется корнями хар-го ур-я λ1 и λ2 . . Решаем хар-е уравнение. Вид общего решения y(x)определяется корнями хар-го ур-я λ1 и λ2 .1. Если λ1 и λ2 действительные и разные, т. е. λ1 ≠ λ2 , то  2. Если λ1 и λ2 действительные и одинаковые, т. е. λ1 = λ2= λ , то  3. Если λ1 и λ2 комплексно-сопряженные числа, т. е. λ = α ± βi, где  , ,  . Здесь C1 и C2 произв пост-е. . Здесь C1 и C2 произв пост-е.Метод отыскания частного решения y (x) * уравнение (1) рассмотрим для двух специальных видов f (x). Пусть  – многочлен степени n, т. е. пусть уравнение имеет вид – многочлен степени n, т. е. пусть уравнение имеет вид 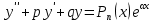 Тогда, если число a совпадает с k корнями (k =1, 2) хар-го ур, то частное решение y* ур-я следует искать в виде 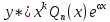 , , 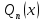 где– полный многочлен той же степени что и где– полный многочлен той же степени что и 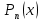 . .Подставляя y* в уравнение (1) и сокращая обе части уравнения на 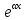 , получаем тождество, из которого, приравниванием коэффициентов при одинаковых степенях, получаем систему для определения значений коэффициентов. Этот метод нахождения y* называется методом неопределенных коэффициентов. , получаем тождество, из которого, приравниванием коэффициентов при одинаковых степенях, получаем систему для определения значений коэффициентов. Этот метод нахождения y* называется методом неопределенных коэффициентов. Замечание 1. Если f (x) = 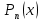 , то следует проверять, совпадает ли число a = 0 с корнями характеристического уравнения. , то следует проверять, совпадает ли число a = 0 с корнями характеристического уравнения.Замечание 2. Если f(x)= 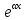 , ,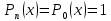 и в этом случае и в этом случае 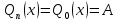 , где A = const . , где A = const . Пусть 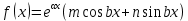 , т. е. пусть ур-е имеет вид , т. е. пусть ур-е имеет вид 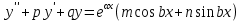 . . Тогда если комплексное число a ± ib совпадает с корнями хар-го ур-я, то частное решение y* следует искать в виде 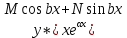 ). ). Если же комплексное число a ± ib не совпадает с корнями хар-го ур-я, то частное решение y* следует искать в виде 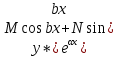 . .При этом неопределенные коэффициенты M и N отыскиваются путем подстановки y* в уравнение с последующим приравн-eм коэффициентов при cosbx и sin bx и решением получившейся системы. Замечание 3. В частном случае, когда 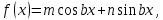 и корни характеристического уравнения λ 2,1 = ±ib, то частное ре- шение y* уравнения следует искать в виде и корни характеристического уравнения λ 2,1 = ±ib, то частное ре- шение y* уравнения следует искать в виде 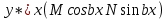 , если же λ 2,1 ≠ ±ib, то , если же λ 2,1 ≠ ±ib, то 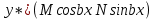 . .Замечание 4. Если 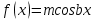 или или 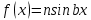 , y* все равно следует искать в общем виде, т. е. и с , y* все равно следует искать в общем виде, т. е. и с 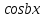 , и с , и с 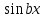 . . |
