Шпоры по дисциплине Высшая математика. 1. Определенный интеграл как предел интегральных сумм. Геометрический смысл определенного интеграла
 Скачать 1 Mb. Скачать 1 Mb.
|
|
32. Общие понятие теории рядов. Свойства рядов. Необходимый признак сходимости числового ряда. Выражение следующего вида: 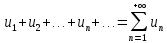 называется рядом, где u1, u2, …, un, …- члены ряда; un- общий член ряда( предполагается, что зависимость от n определена). называется рядом, где u1, u2, …, un, …- члены ряда; un- общий член ряда( предполагается, что зависимость от n определена).Сумма n первых членов ряда 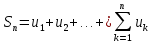 называется n-й частичной суммой ряда, а выражение Rn=un+1+un+2+…= называется n-й частичной суммой ряда, а выражение Rn=un+1+un+2+…=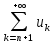 - n-м остатком ряда. - n-м остатком ряда.Свойства числовых рядов: 1) если к ряду 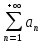 прибавить (или отбросить) конечное число членов, то полученный ряд и ряд прибавить (или отбросить) конечное число членов, то полученный ряд и ряд 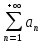 сходятся или расходятся одновременно; сходятся или расходятся одновременно;2) если ряд 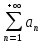 сходится и его сумма равна S, то ряд сходится и его сумма равна S, то ряд 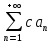 , где с – произвольное число, также сходится и его сумма равна cS. Если же ряд , где с – произвольное число, также сходится и его сумма равна cS. Если же ряд 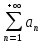 расходится и с≠0, то и ряд расходится и с≠0, то и ряд 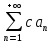 раасходится; раасходится;3) если 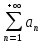 и и 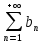 сходятся, а их суммы равны S1 и S2 соответственно, то сходится и ряды сходятся, а их суммы равны S1 и S2 соответственно, то сходится и ряды 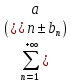 , причем , причем 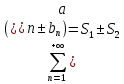 ; ;4)члены сходящегося ряда можно группировать произвольным образом, не переставляя их местами. Необходимый признак сходимости ряд. Если числовой ряд 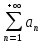 сходится, то его общий член стремится к нулю, т.е. сходится, то его общий член стремится к нулю, т.е. 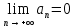 33. Признаки сходимости рядов с положительными членами. Признаки сравнения. Признак даламбера : если 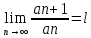 то при 0 ≤ l <1 ряд (А) сходится, при l >1 ряд расходится, при l =1вопрос о сходимости ряда остается открытым. то при 0 ≤ l <1 ряд (А) сходится, при l >1 ряд расходится, при l =1вопрос о сходимости ряда остается открытым.Интегральный признак Коши Пусть члены ряда (А) могут быть представлены как значения некоторой неотрицательной, непрерывной, убывающей на промежутке [1, + ∞) функции f (х): a1 = f (1), a2 = f (2), ..., an = f (n), ... Тогда ряд (А) и несобственный интеграл 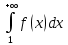 сходятся (или расходятся) одновременно. Непредельный признак сравнения. Пусть an ≤ bn для всех n или начиная с некоторого номера. Тогда из сходимости ряда (В) следует сходимость ряда (А), а из расходимости ряда (А) – расходи- мость ряда (В). Предельный признак сравнения. Если существует конечный и отличный от нуля предел 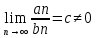 то ряды (А) и (В) сходятся (или расходятся) одновременно. то ряды (А) и (В) сходятся (или расходятся) одновременно.Замечание. Признак Даламбера целесообразно применять, когда общий член ряда содержит выражения вида n! или 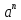 . .34. Признаки сходимости рядов с положительными членами. Интегральный признак Коши . Степенной признак сравнения. Интегральный признак Коши 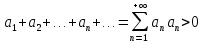 Пусть члены ряда (А) могут быть представлены как значения некоторой неотрицательной, непрерывной, убывающей на промежутке 1, функции f (х): a1 f (1), a2f (2), ..., anf (n), ... Тогда ряд (А) и несобственный интеграл 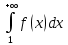 сходятся (или расходятся) одновременно. сходятся (или расходятся) одновременно.Признаки сравнения Наряду с рядом (А) рассмотрим ряд: 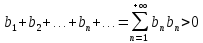 Непредельный признак сравнения. Пусть an ≤ bn для всех n или начиная с некоторого номера. Тогда из сходимости ряда (В) следует сходимость ряда (А), а из расходимости ряда (А) – расходи- мость ряда (В). Предельный признак сравнения. Если существует конечный и отличный от нуля предел 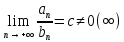 то ряды (А) и (В) сходятся (или расходятся) одновременно. 1) с рядом геометрической прогрессии 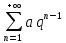 который сходится при q <1; который сходится при q <1;2) гармоническим рядом 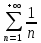 который расходится; который расходится;3) обобщенным гармоническим рядом 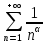 сходится при (α>1 и расходится при α1).) сходится при (α>1 и расходится при α1).)35 .Знакочередующиеся ряды. Признак Лейбница: Числовой ряд 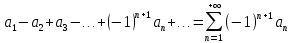 , где , где 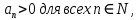 называется знакочередующимся. называется знакочередующимся.Признак сходимости знакочередующегося ряда (признак Лейбница). Если для знакочередующегося ряда 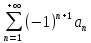 выполнены условия: выполнены условия:Модули членов ряда монотонно убывают: 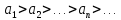 Предел общего члена ряда равен нулю: 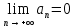 ,то ряд сходится и его сумма не превосходит первого члена ,то ряд сходится и его сумма не превосходит первого члена 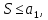 а остаток ряда а остаток ряда 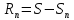 удовлетворяет неравенству удовлетворяет неравенству 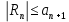 Ряды, для которых выполняется признак Лейбница, называются рядами Лейбница (лейбницевского типа). 36. Общий достаточный признак сходимости знакопеременных рядов. Абсолютная и условная сходимости числовых рядов. Свойства абсолютно сходящихся рядов. Достаточный признак сходимости знакопеременного ряда: если сходится ряд 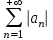 , составленный из модулей членов знакопеременного ряда , составленный из модулей членов знакопеременного ряда  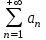 , то сходится и знакопеременный ряд , то сходится и знакопеременный ряд 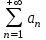 Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Условно сходящийся – если сам ряд сходится, а ряд, составленный из модулей его членов, расходится. Абсолютно сходящиеся ряды обладают не только всеми свойствами сходящихся рядов, но и дополнительно свойствами сумм конечного числа слагаемых. Такие ряды можно:1)перемножать 2)переставлять местами члены ряда 3)подставлять «ряд в ряд» 37. Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом 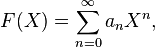 Теорема Абеля. Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом Е  сли степенной ряд сли степенной ряд 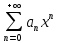 сходится при сходится при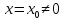 то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству 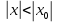 ; если же ряд расходится при ; если же ряд расходится при 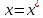 , то он расходится при всех значениях х, удовлетворяющих неравенству , то он расходится при всех значениях х, удовлетворяющих неравенству 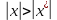 . .38. Ряды Тейлора и Маклорена. Достаточные условия разложимости функции в ряд Тейлора. Пусть функция () f x определена и дифференцируема в окрестности точки a любое число раз. Рядом Тейлора для функции ()y fx= в окрестности точки x a = называется ряд вида 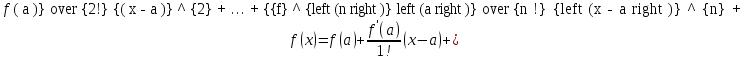 В частности, при а=0 получаем ряд Маклорена: 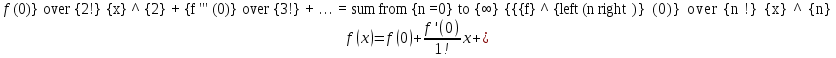 Чтобы получить разложение функции () f x в ряд Тейлора, нужно вычислить значения данной функции и всех ее производных в точке , a т. е. найти ( ), f а ( ), f а ′ ( ),..., f а ′′ и записать формально ее ряд Тейлора по формуле. Затем найти область сходимости полученного ряда и выяснить, в каких точках из области сходимости суммой ряда будет ( ). Если в некоторой окрестности заданной точки функция раскладывается в степенной ряд, то это разложение единственно 39. Разложение некоторых элементарных функций в ряд Маклорена. 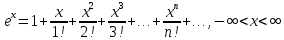 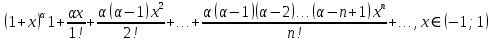 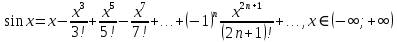 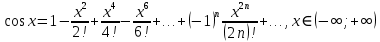 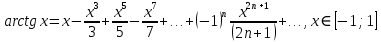 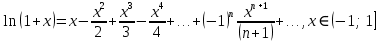 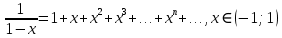 40. Приближённое решение дифференциальных уравнений: Приближенное вычисление значений функций. Пусть дан степенной ряд функции y=f(x). Задача вычисления значения этой функции при x=x0 заключается в отыскании суммы ряда с заданной точностью ε > 0, которую можно достичь путем оценивания остатка числового ряда, ограничиваясь определенным числом членов ряда. Приближенное вычисление определенных интегралов. Степенные ряды применяются для приближенного вычисления определенных интегралов 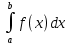 в случаях, если первообразная не выражается в конечном виде через элементарные функции или нахождение первообразной сложно. Если подынтегральная функция f(x) разложима в степенной ряд по степеням x и интервал сходимости (−R, R) включает в себя отрезок интегрирования [a, b], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. в случаях, если первообразная не выражается в конечном виде через элементарные функции или нахождение первообразной сложно. Если подынтегральная функция f(x) разложима в степенной ряд по степеням x и интервал сходимости (−R, R) включает в себя отрезок интегрирования [a, b], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда.В случае, когда точное решение задачи Коши для ДУ в элементарных функциях не представляется возможным или оказывается очень сложным, это решение(если оно представимо) удобно искать в виде степенного ряда. 40.При решении задачи Коши 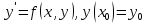 используем ряд Тейлора: используем ряд Тейлора: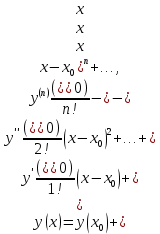 Где 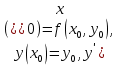 а остальные производные а остальные производные 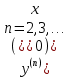 ) находят путем последовательного дифференцирования уравнения и подстановки начальных данных в выражения для этих производных. ) находят путем последовательного дифференцирования уравнения и подстановки начальных данных в выражения для этих производных.41. Дискретное вероятностное пространство. В дискретном вероятностном пространстве, связанном с данным случайным экспериментом, множество 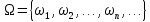 возможных элементарных событий не более чем счетно; вероятности элементарных событий заданы( P(ω1)=p1,…), причем pi≥0 и возможных элементарных событий не более чем счетно; вероятности элементарных событий заданы( P(ω1)=p1,…), причем pi≥0 и 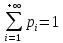 ( условие контроля). Множество Ω- достоверное событие. Под случайным событием А= ( условие контроля). Множество Ω- достоверное событие. Под случайным событием А=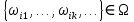 понимается совокупность элементарных событий понимается совокупность элементарных событий  , называемых элементарными исходами, благоприятствующими появлению события А: , называемых элементарными исходами, благоприятствующими появлению события А:  . Событие, не содержащее ни одного элементарного исхода, называется невозможным. . Событие, не содержащее ни одного элементарного исхода, называется невозможным. Вводятся следующие операции над событиями: 1)суммой А+В событий А и В называется событие С=А+В, состоящее в наступлении хотя бы одного из событий А или В (или А, или В, или оба) 2) произведением А*В=АВ событий А и В называется событие С=АВ, состоящее в том, что в результате случайного эксперимента произошли и событие А, и событие В. Два события А и  называются противоположными, если называются противоположными, если  и и  , то есть в данном случайном эксперименте они несовместны и одно из них обязательно происходит. , то есть в данном случайном эксперименте они несовместны и одно из них обязательно происходит. 42. Классическое вероятностное пространство. Геометрическая вероятность. В приложениях ТВ широко используется понятие геометрической вероятности. СЭ заключается в том, что исследуемая точка случайным образом (наудачу) появляется в любой точке заданного измеримого геометрического множества Ω. Событие A состоит в том, что исследуемая точка появляется в подмножестве A множества Ω: A ⊂ Ω. Если S – геометрическая мера (длина, площадь, объем) всей области, а SA – геометрическая мера части этой области, попадание в которую благоприятствует появлению данного события А, то вероят- ность этого события определяется формулой  Классическое определение вероятности. Пусть с СЭ связано конечное число n равновозможных элементарных исходов. Тогда вероятность P(А) события А, связанного с данным СЭ, определяется формулой  43. 44. Теоремы сложения, умножения вероятностей. Несовместные, независимые события. Теорема сложения вероятностей. Вероятность суммы двух событий равна сумме вероятностей этих событий за вычетом вероятности их произведения: для любых событий А и В: P(A+B)=P(A)+P(B)-P(AB). Теорема сложения вероятностей несовместных событий: P(A+B)=P(A)+P(B), если А и В – несовместны, в частности ,Р(А)+Р(  )=1. )=1.Вероятность Р(А│В) появление в СЭ события А, если известно, что в этом СЭ произошло событие В,- условная вероятность- определяется соотношением Р(А|В)=  . .Отсюда следует теорема умножения вероятностей: Р(АВ)=Р(А)Р(В|А)=Р(В)Р(А|В). События А и В называются независимыми, если появление одного из них не зависит от появления другого, точнее, Р(А|В)=Р(А), P(B|A)=P(B). В противном случае события А и В называются зависимыми. Теорема умножения вероятностей независимых событий: P(AB)=P(A)P(B), если А и В независимы. 45. Формула полной вероятности. События А1, А2, …, Аn образуют полную группу для данного СЭ, если: 1) AiAj =∅ для i ≠ j; 2) А1 + А2 + …+ Аn = Ω, т. е. а) они попарно несовместны и б) в результате СЭ обязательно появится одно из них. Для одного и того же СЭ можно рассматривать различные полные группы событий, например события А и A, где А – любое событие, связанное с СЭ, всегда образуют полную группу событий. Если событие А может наступить при появлении одного из n попарно несовместных событий (гипотез) H1, H2 , …, Hn , образующих полную группу событий, то вероятность события А можно вычислить по формуле полной вероятности: P(A)=P(H1)P(A|H1)+P(H2)P(A|H2)+…+P(Hn)P(A|Hn), причем P(H1)+ P(H2)+…+ P(Hn)=1. Если событие А произошло, то это может изменить вероятности гипотез P(H1), P(H2), …, P(Hn). По теореме умножения вероятностей P(AB1)=P(B1)P(A|B1)=P(A)P(B|A), откуда  Аналогично, для остальных гипотез  . .Полученная формула называется формулой Байеса. Вероятности гипотез P(Bi|A) называются апостериорными вероятностями, тогда как P(Bi) - априорными вероятностями. |
