интегрирование. КР 4. Решение Полагаем. Тогда, Тогда исходный интеграл можно записать так, подставим вычисленные интегралы
 Скачать 36.2 Kb. Скачать 36.2 Kb.
|
|
Вариант 1.4 Найти неопределённые интегралы 1. 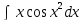 Решение: Полагаем  . Тогда . Тогда 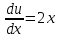 , , 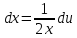 Тогда исходный интеграл можно записать так: 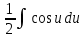 . .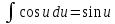 , подставим вычисленные интегралы: , подставим вычисленные интегралы: . Производим обратную замену . Производим обратную замену  , ,  . .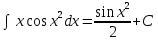 . .2.  Решение: Полагаем 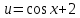 . Тогда . Тогда 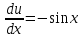 , ,  Тогда исходный интеграл можно записать так: 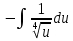 . .Вычисляем  , подставим вычисленные интегралы: , подставим вычисленные интегралы: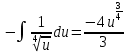 . Производим обратную замену . Производим обратную замену 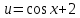 , ,  . . . .3. 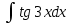 Решение: Полагаем  . Тогда . Тогда  , ,  Тогда исходный интеграл можно записать так: 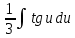 . .Вычисляем  Полагаем 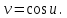 Тогда Тогда 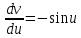 , , 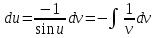 . .Вычисляем 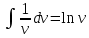 , подставим вычисленные интегралы: , подставим вычисленные интегралы: . Производим обратную замену . Производим обратную замену  , ,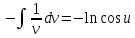 . . Подставим вычисленные интегралы 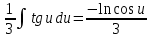 . Производим обратную замену . Производим обратную замену   +C= +C= . .4.  Решение: Полагаем 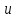 = = . Тогда . Тогда  , ,  Тогда исходный интеграл можно записать так: 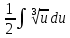 . .Вычисляем 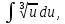 находим интеграл от степенной функции находим интеграл от степенной функции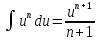 при n= при n= , , 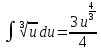 , подставим вычисленные интегралы: , подставим вычисленные интегралы: 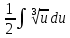 = =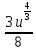 . Производим обратную замену . Производим обратную замену  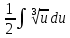 = =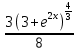 . .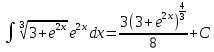 5.  Решение: Производим интегрирование по частям: 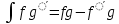 , , , ,  . . Полагаем  . Тогда . Тогда  , , 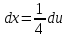 , записываем , записываем  . . , подставим вычисленные интегралы: , подставим вычисленные интегралы:  = = . Производим обратную замену . Производим обратную замену  , ,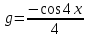  , дифференцируем 2х+1 почленно: , дифференцируем 2х+1 почленно: Тогда исходный интеграл можно записать так:  , ,Далее вычисляем  , , Полагаем  . Тогда . Тогда  , ,  , соответственно , соответственно  , ,Находим  , подставим вычисленные интегралы: , подставим вычисленные интегралы: . Производим обратную замену . Производим обратную замену  , , , подставим вычисленные интегралы: , подставим вычисленные интегралы: , ,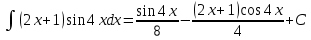 6. 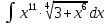 Решение: Полагаем  . Тогда . Тогда  , , 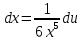 Тогда исходный интеграл можно записать так: 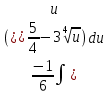 , Далее вычисляем , Далее вычисляем  применим свойство линейности: применим свойство линейности:  . . Вычисляем  , интеграл от степенной функции , интеграл от степенной функции 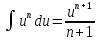 при n= при n=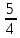 , , 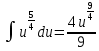 . .Вычисляем 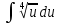 , интеграл от степенной функции при n= , интеграл от степенной функции при n=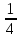 , ,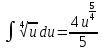 . .Подставляем вычисленные интегралы :  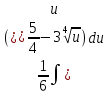 = = . Производим обратную замену . Производим обратную замену  , , = = . . = = +c +c7. 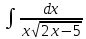 Решение: Полагаем  . Тогда . Тогда 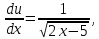  Тогда исходный интеграл можно записать так: 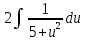 . .Далее вычисляем 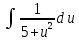 . Полагаем . Полагаем 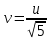 Тогда Тогда  , ,  , соответственно , соответственно  Далее вычисляем  подставим вычисленные интегралы: подставим вычисленные интегралы:  . Производим обратную замену . Производим обратную замену   . .Подставляем вычисленные интегралы :  . Производим обратную замену . Производим обратную замену , , . . 8.  Решение: Вычислить определённые интегралы 10. 3 2 0 ln( 3) e x dx ; 11. 0 cos7xcos2xdx . Вычислить несобственные интегралы или установить их расходимость 12. 2 0 6 34 dx x x ; 13. 3 1 ln3 e dx x x . Выяснить сходимость несобственных интегралов 14. 3 2 6 1 6 9 5 4 x x dx x x ; 15. 1 2 0 cos sin 2 x dx x x . 38 16. Найти площадь области, ограниченной линиями 2 2 , , 3 x x y e y e x . 17. Найти длину дуги кривой y ln x, 3 x 4 . |
