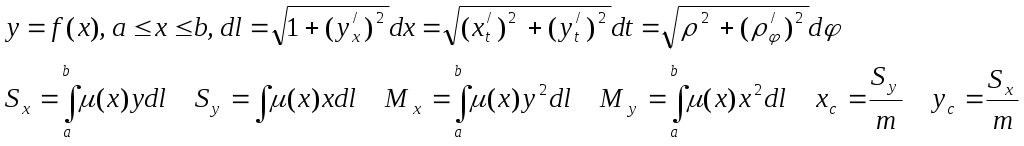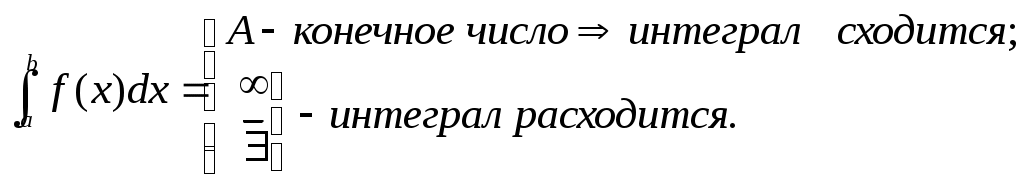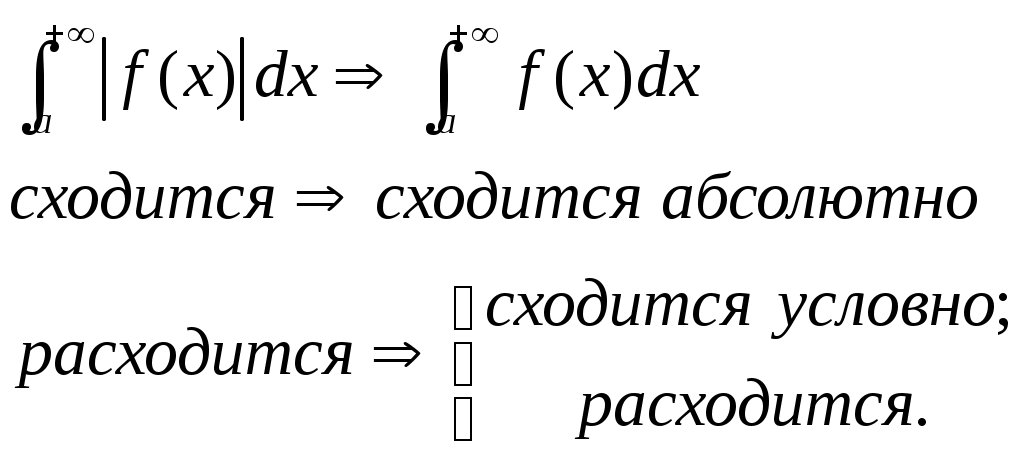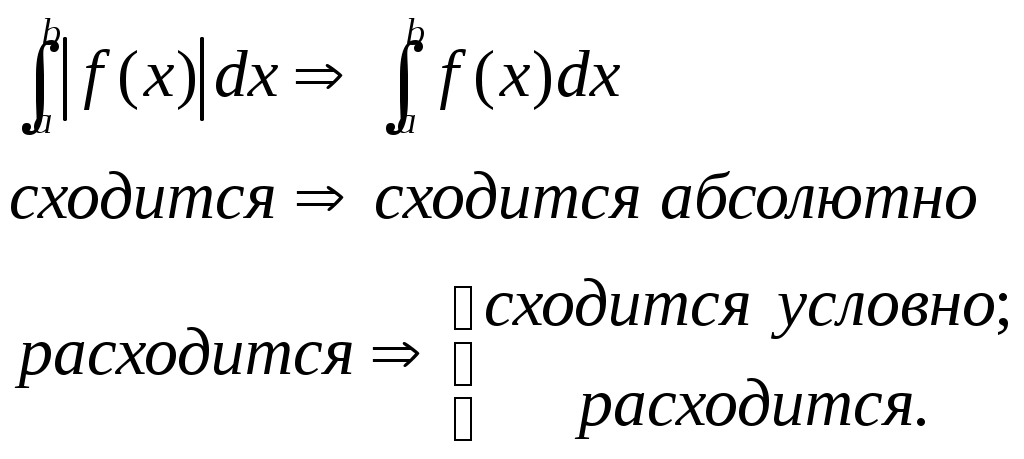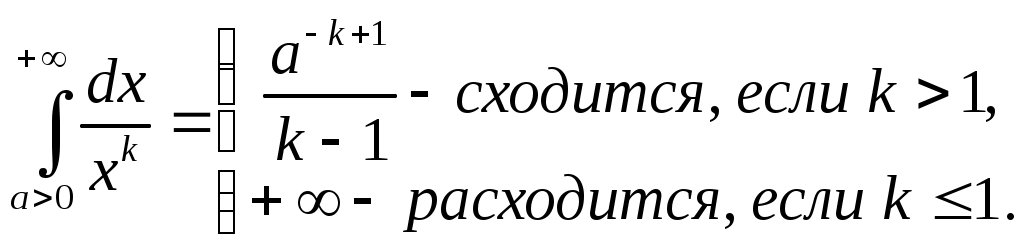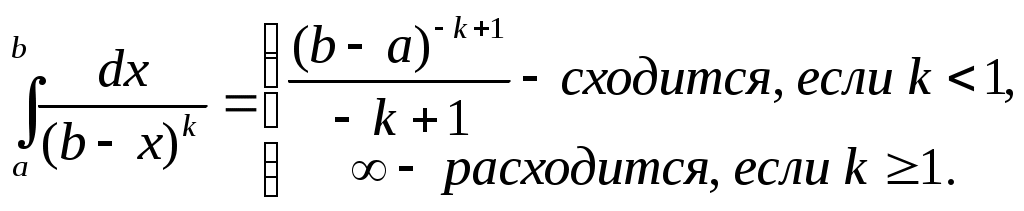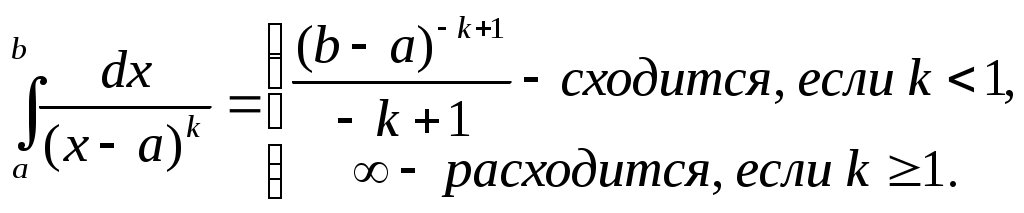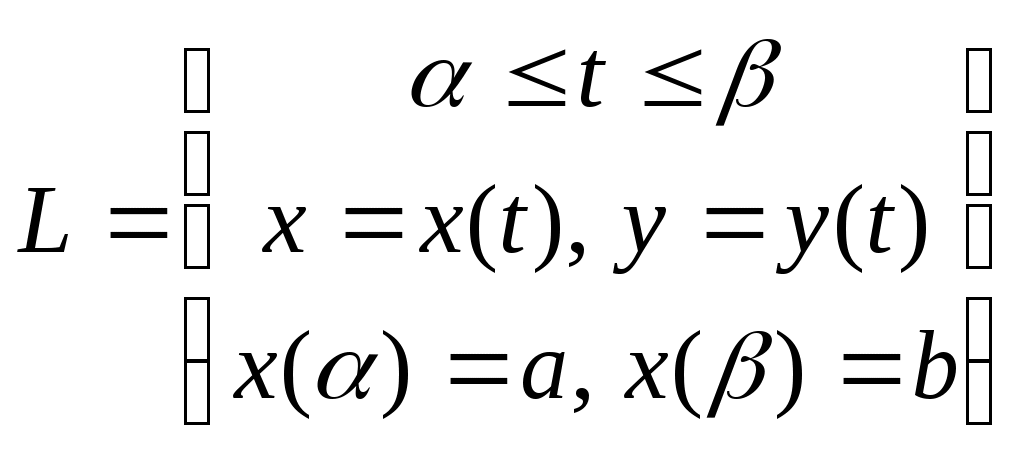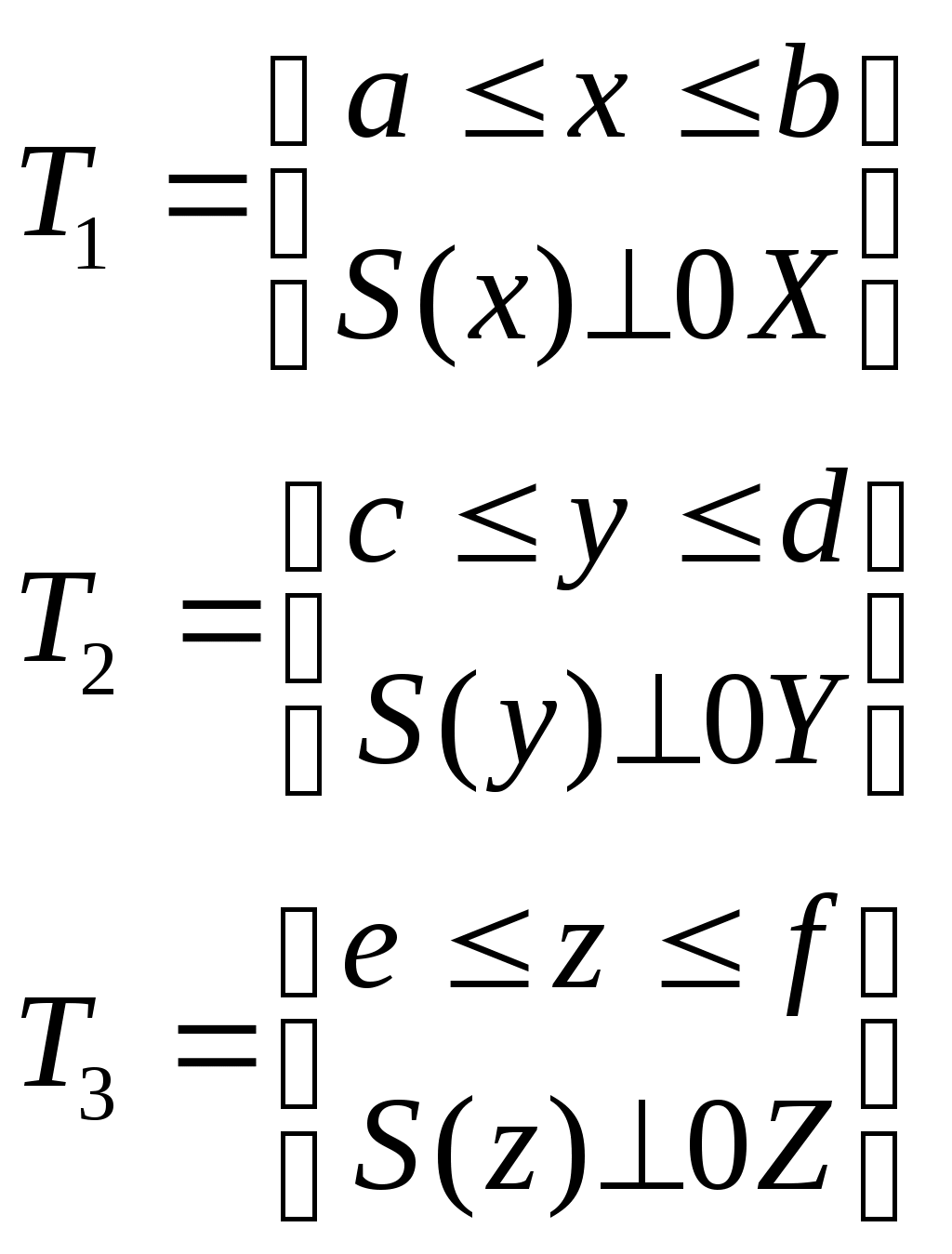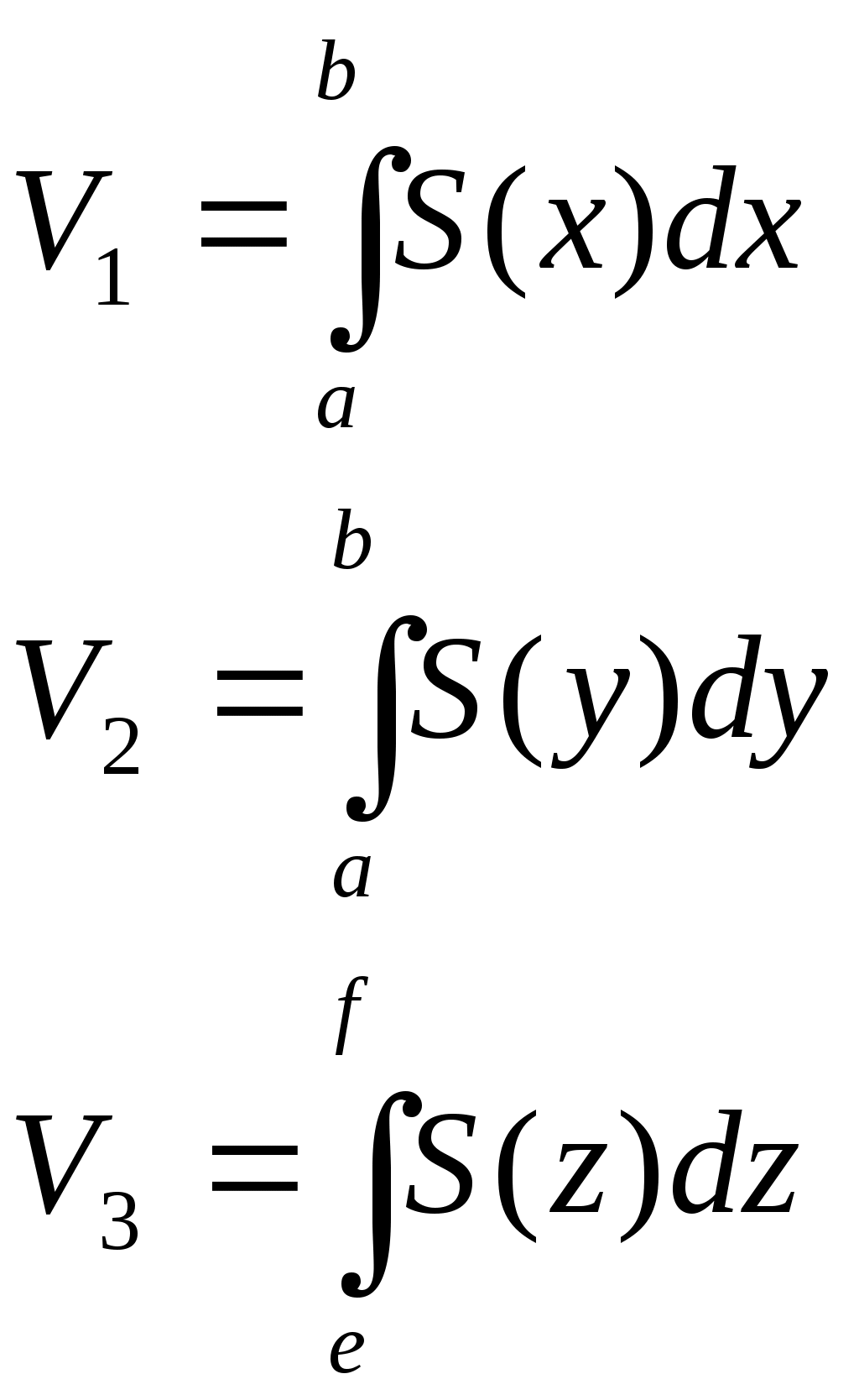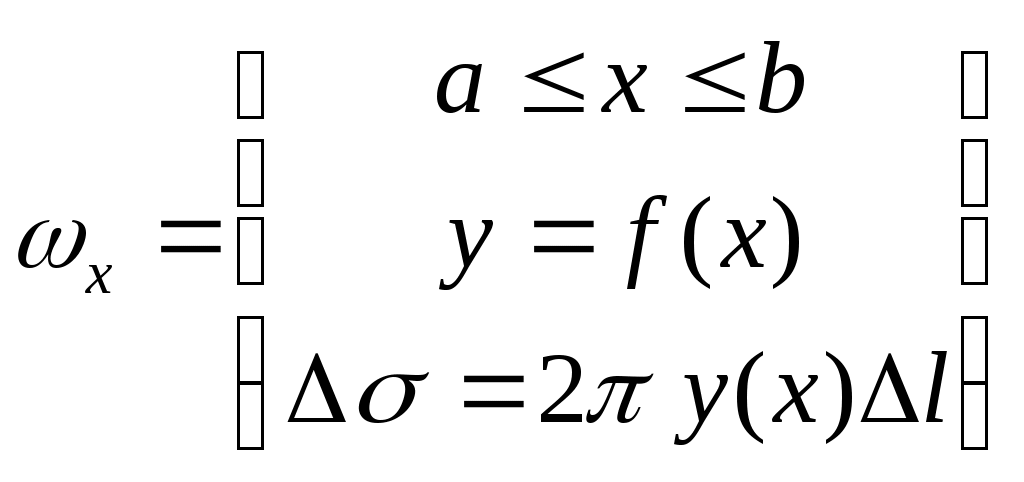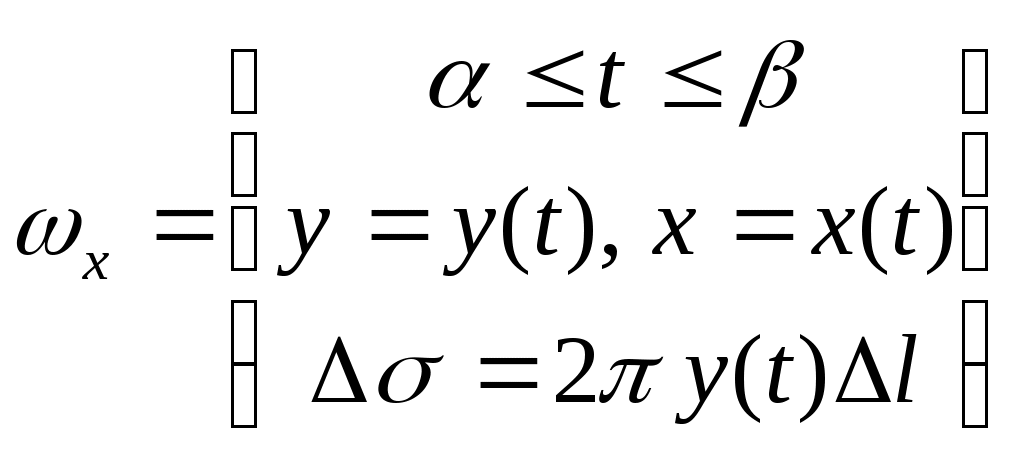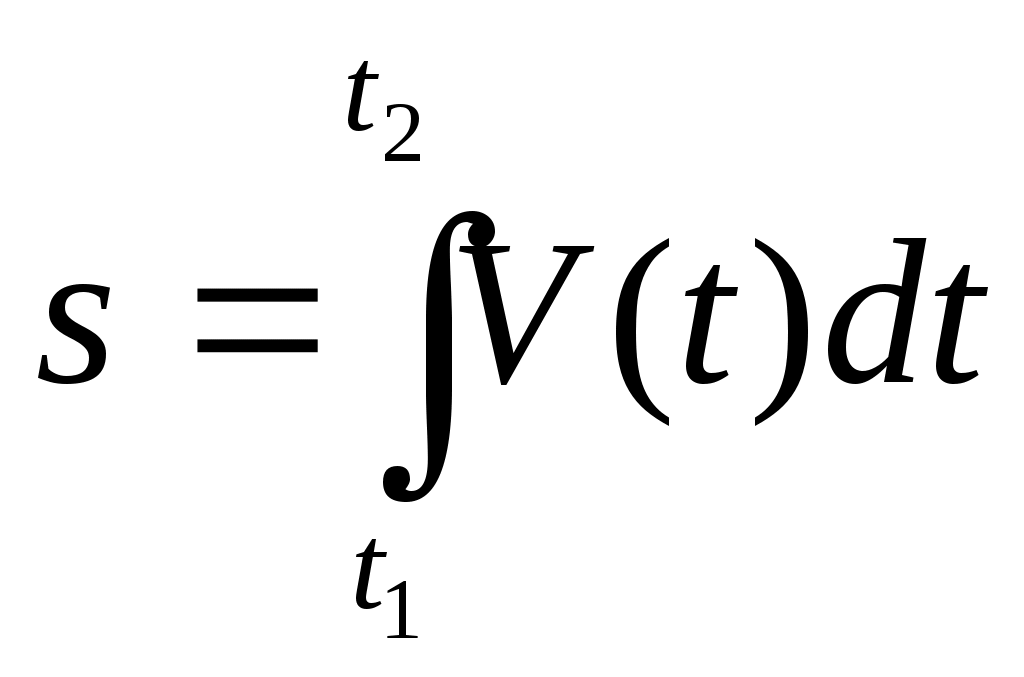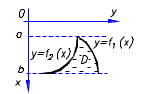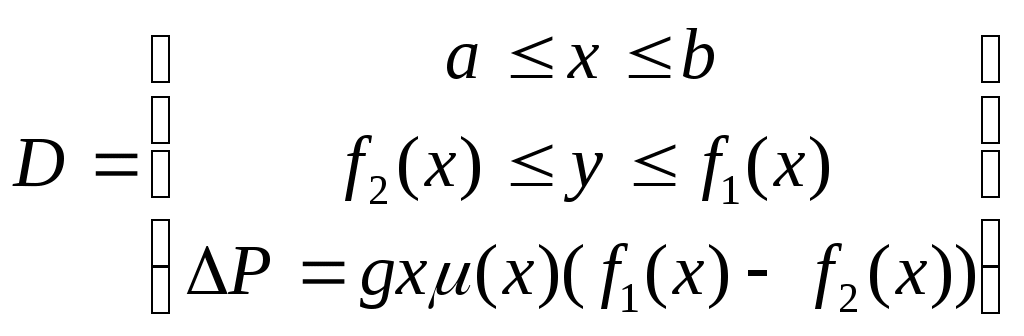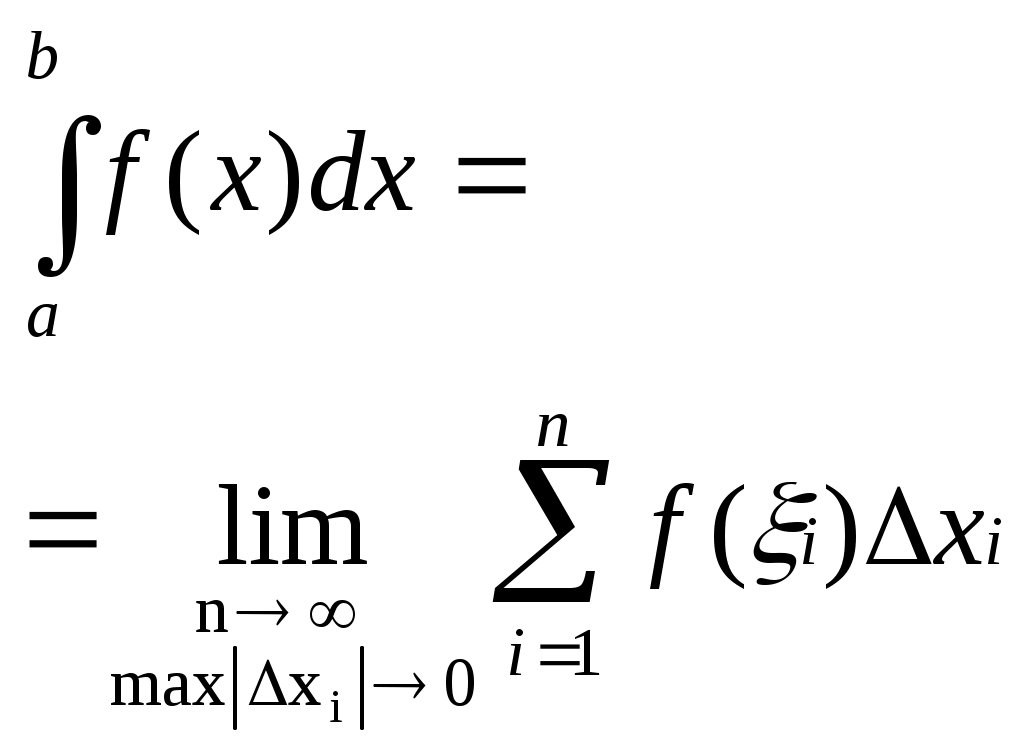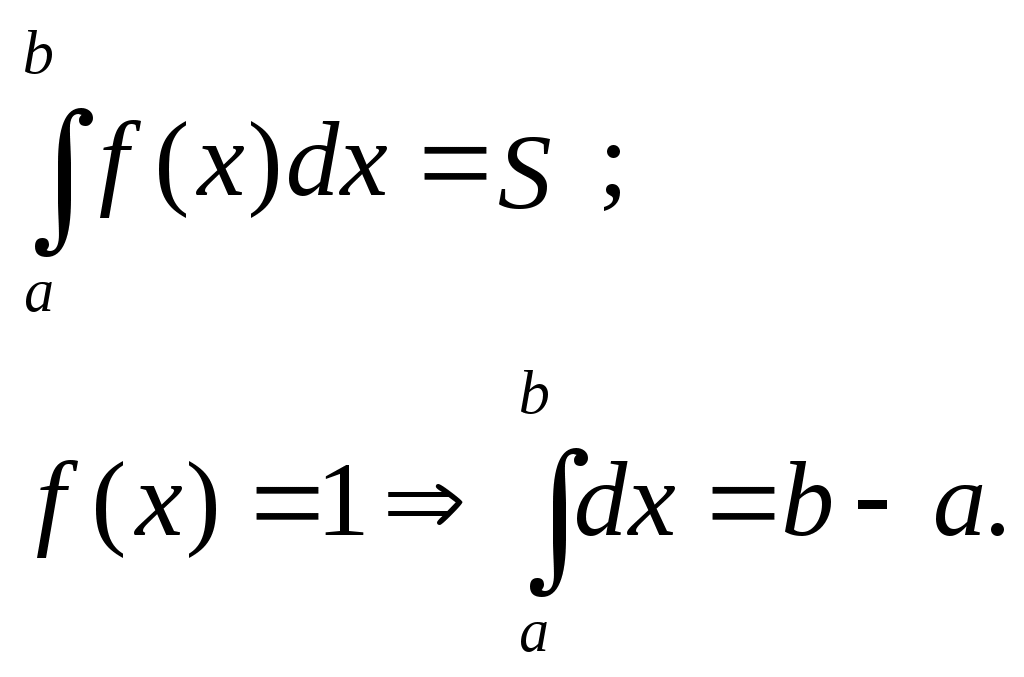|
|
Опорные конспекты. Несобственные интегралы (н и.)
Несобственные интегралы (н.и.)
|
I рода
(по бесконечному промежутку)
|
II рода (от неограниченной
на промежутке интегрирования функции)
|
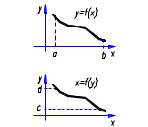
Определение н.и.
|
1
|
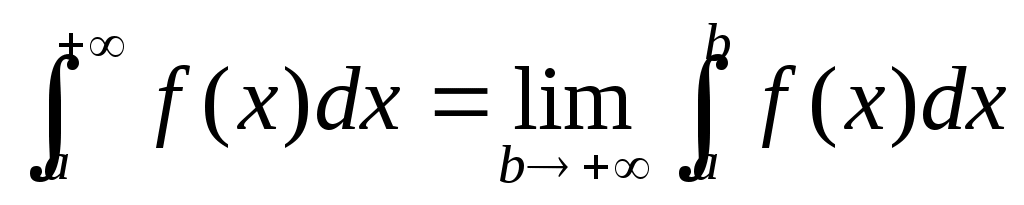
|
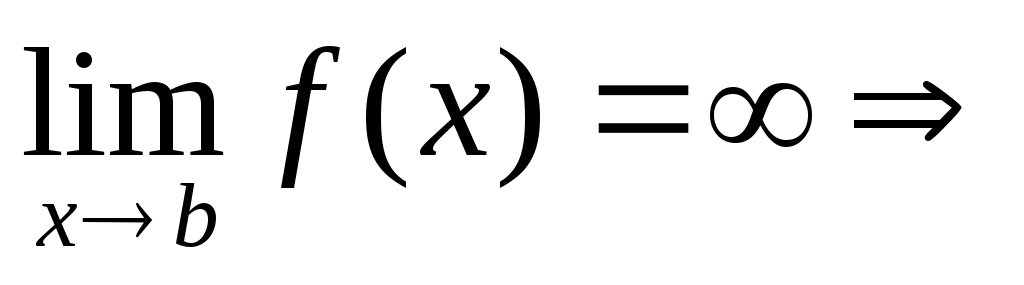 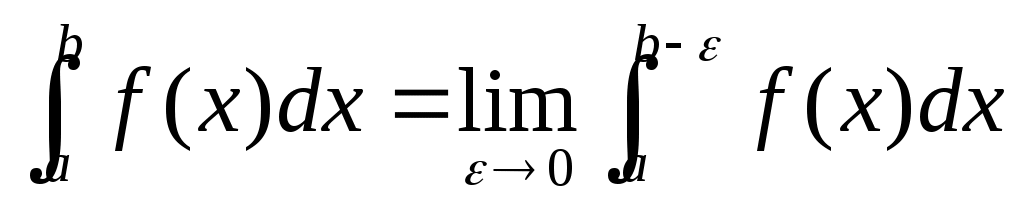
|
2
|
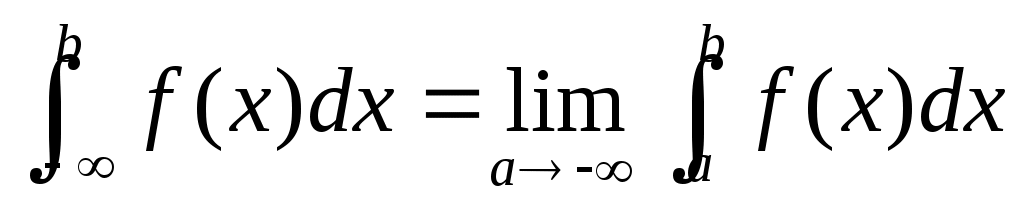
|
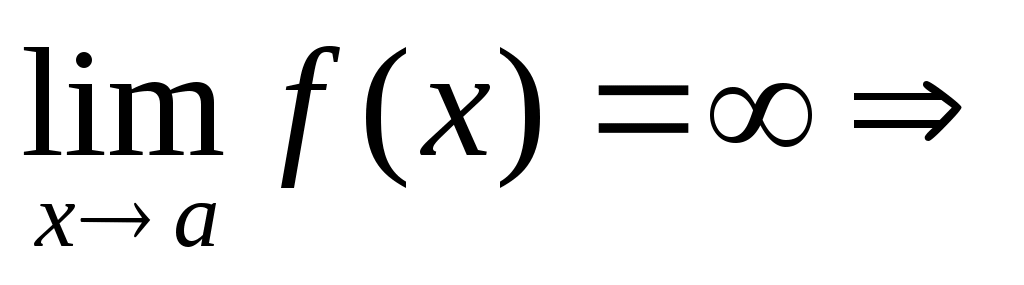 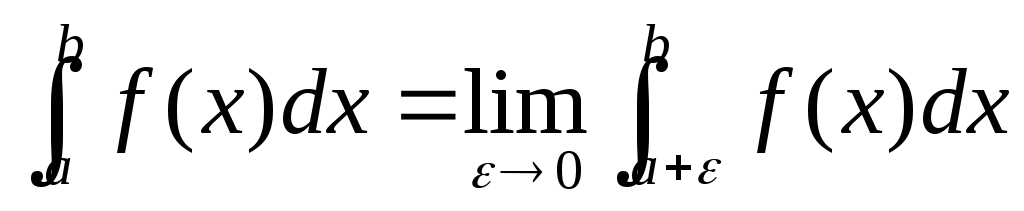
|
3
|
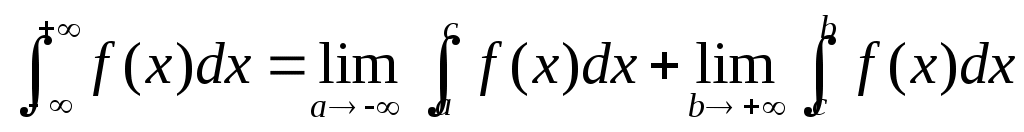
|
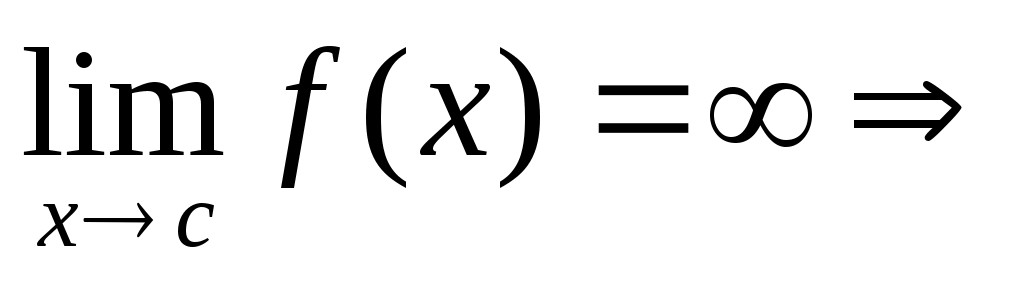 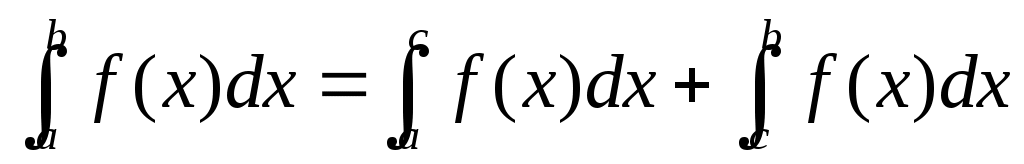
|
Определение сходимости н.и.
|
Несобственный интеграл сходится, если существуют конечные пределы в правых частях равенств, определяющих эти интегралы.
Если эти пределы бесконечны или не существуют, то несобственный интеграл расходится.
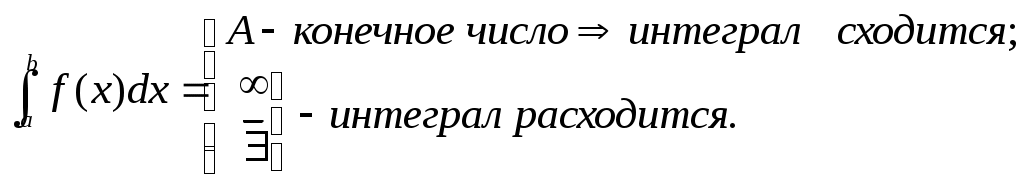
|
Признаки сходимости н.и.
|
1
|
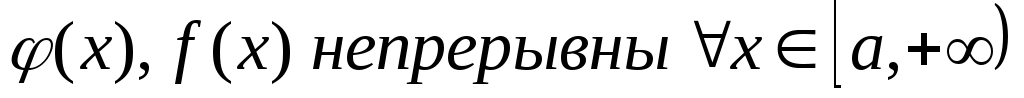
|
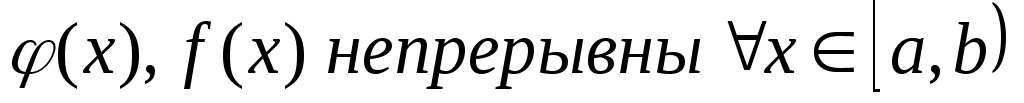
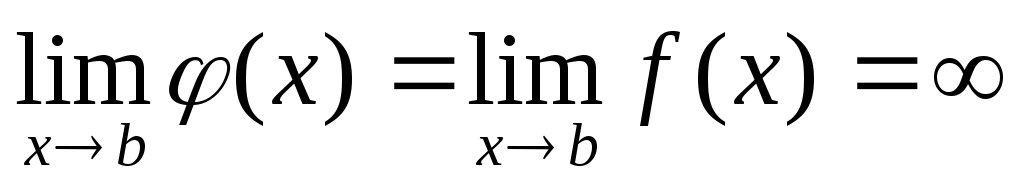
|
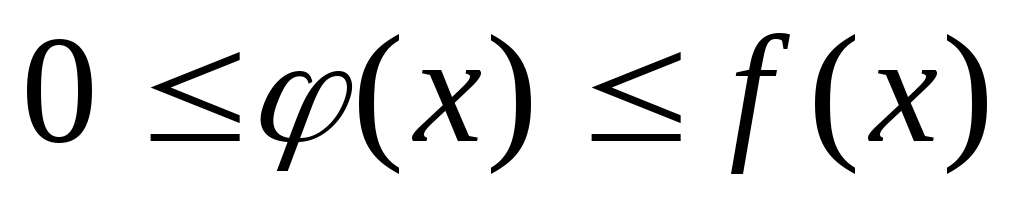
|
Сходимость
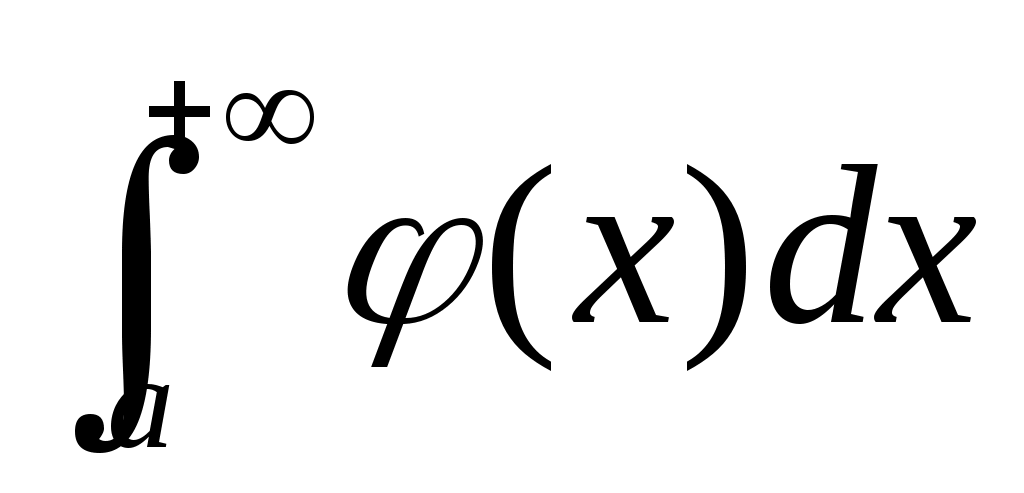 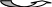 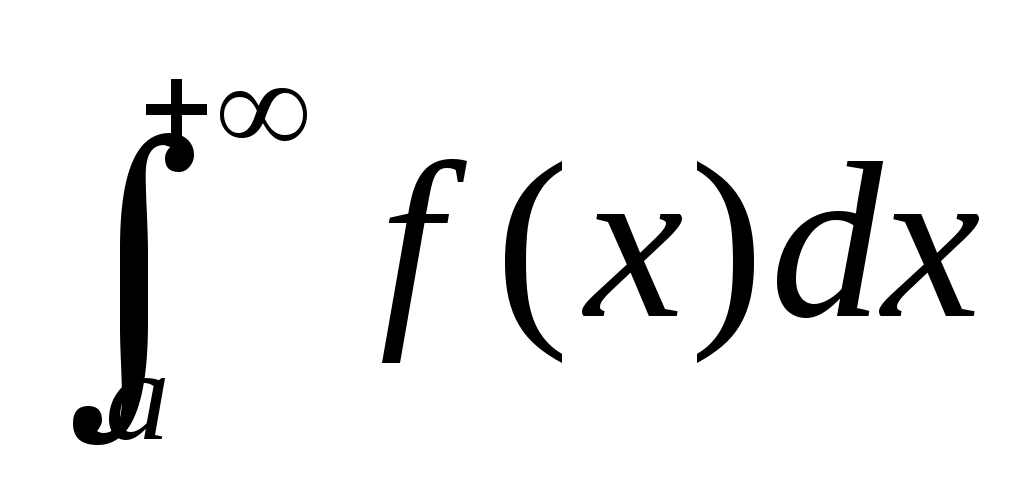
Расходимость
|
Сходимость
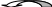
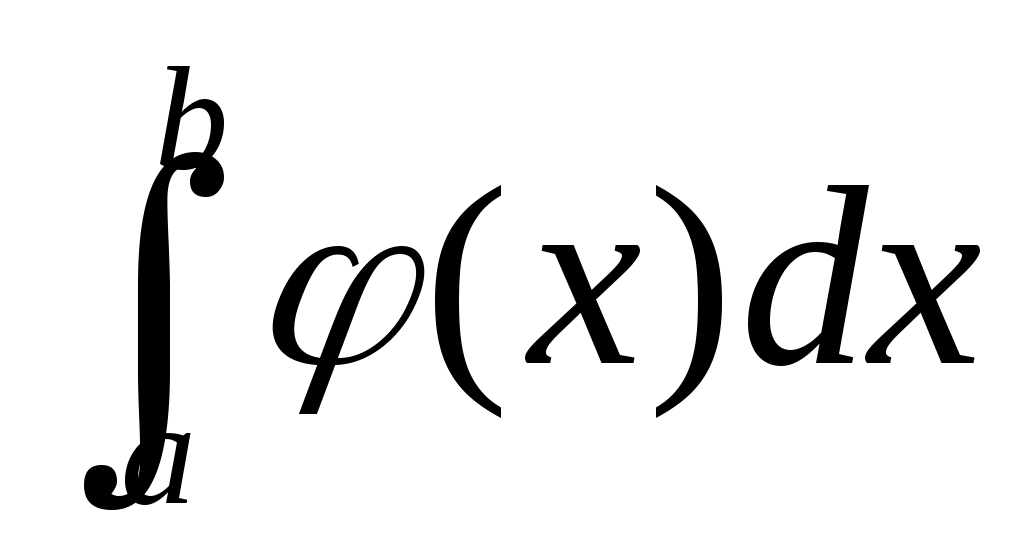 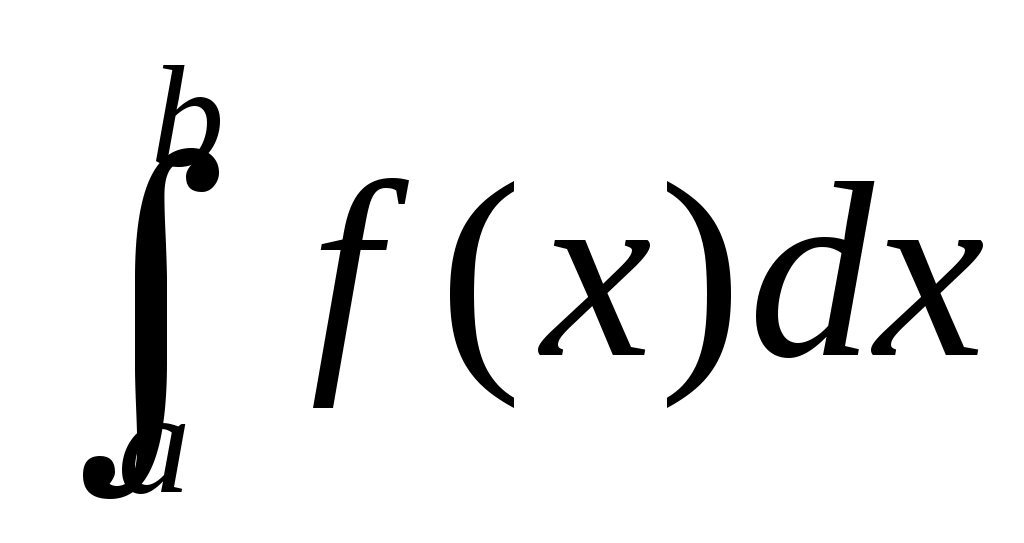
Расходимость
|
2
|
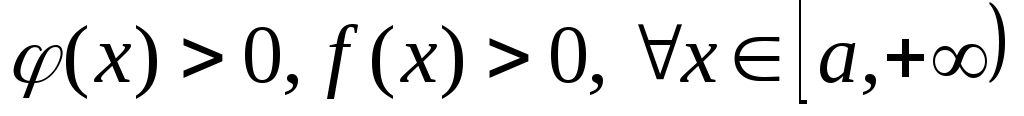
|
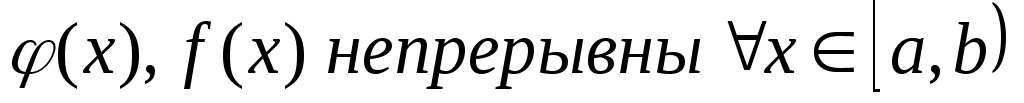
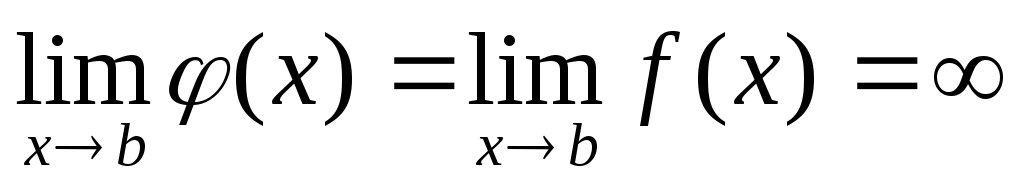
|
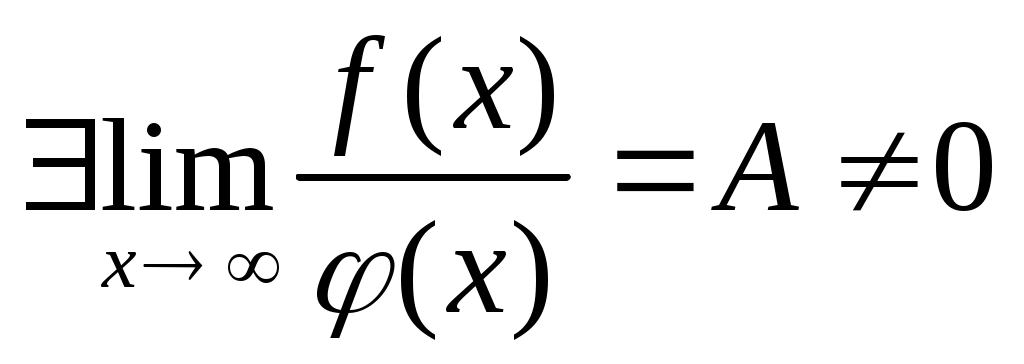
|
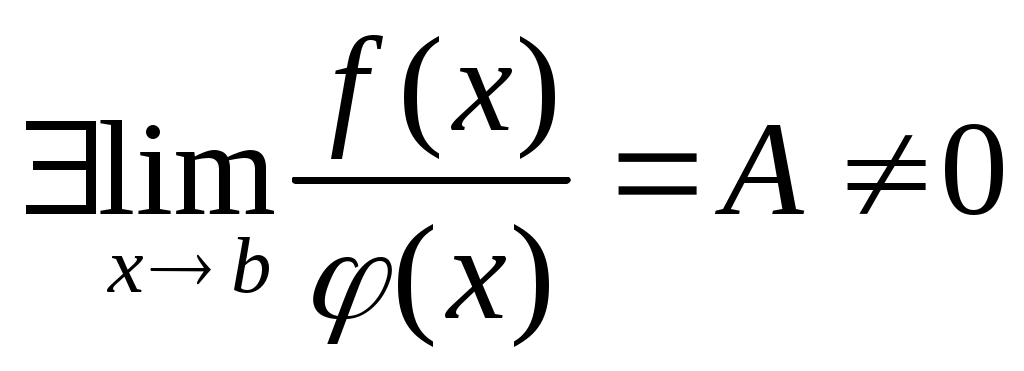
|
Несобственные интегралы от функций 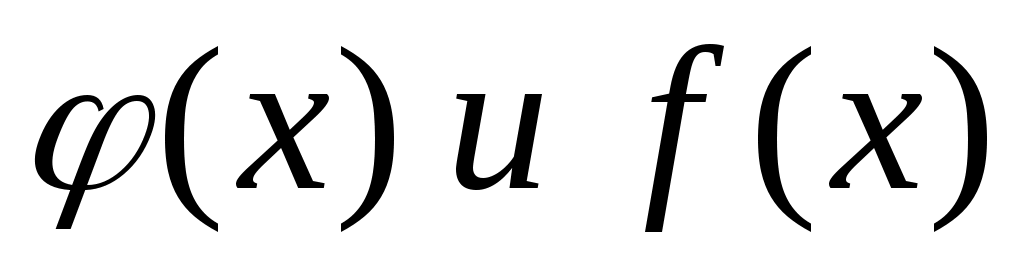 ведут себя одинаково: ведут себя одинаково:
или оба сходятся, или оба расходятся
|
3
|
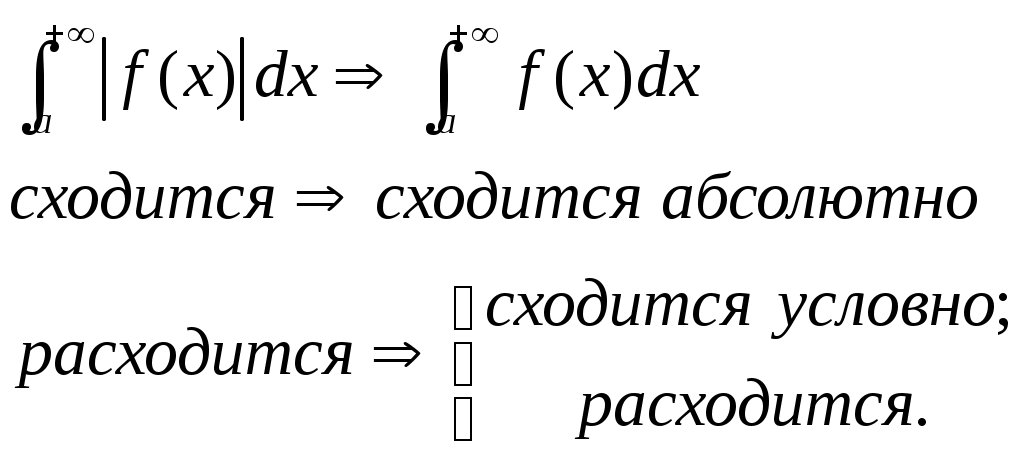
|
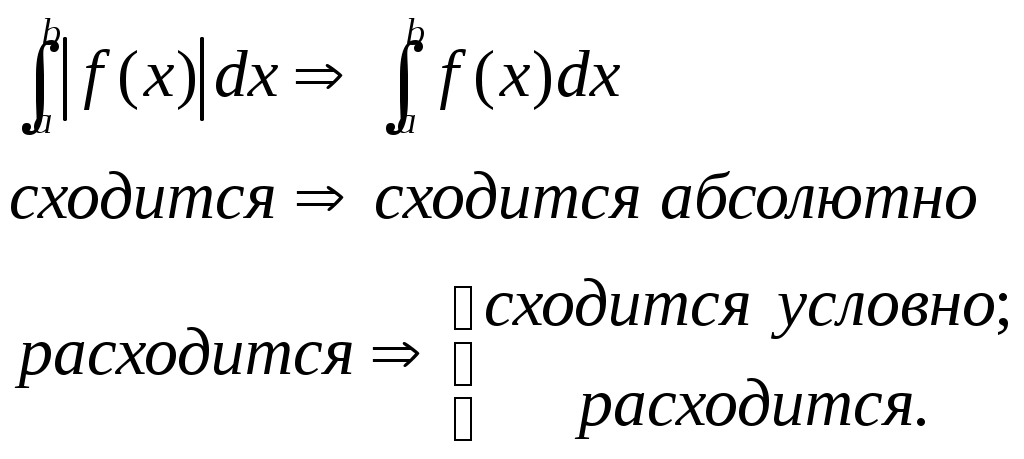
|
Эталонные н.и.
|
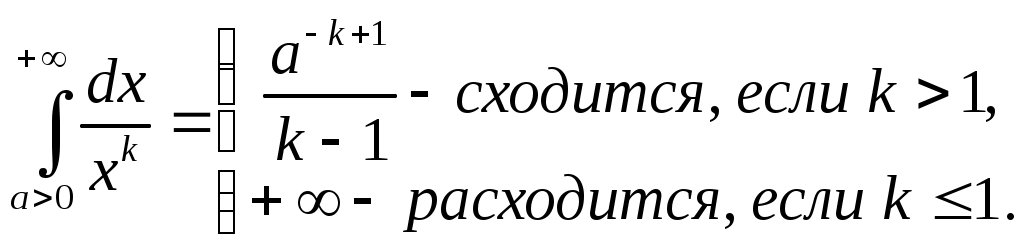
|
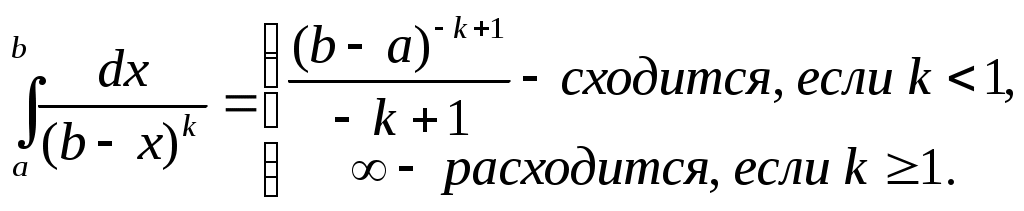 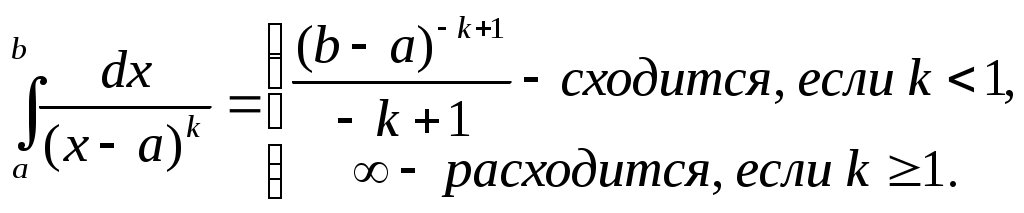
|
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Теорема. Если величина Q обладает на [a,b]
свойством аддитивности, а именно, если a = x0 x1 x2 …xn = b,
то Q=Q1+Q2+…+Qn, где Qi – значение Qна [xi-1,xi], i=1,2,…n;
свойством линейности Q в малом: Qf(x)x, где f(x) – интегрируемая на [a,b]функция,
то величину Qможно найти интегралом от ее элемента dQ = f(x)dx по промежутку [a,b]:
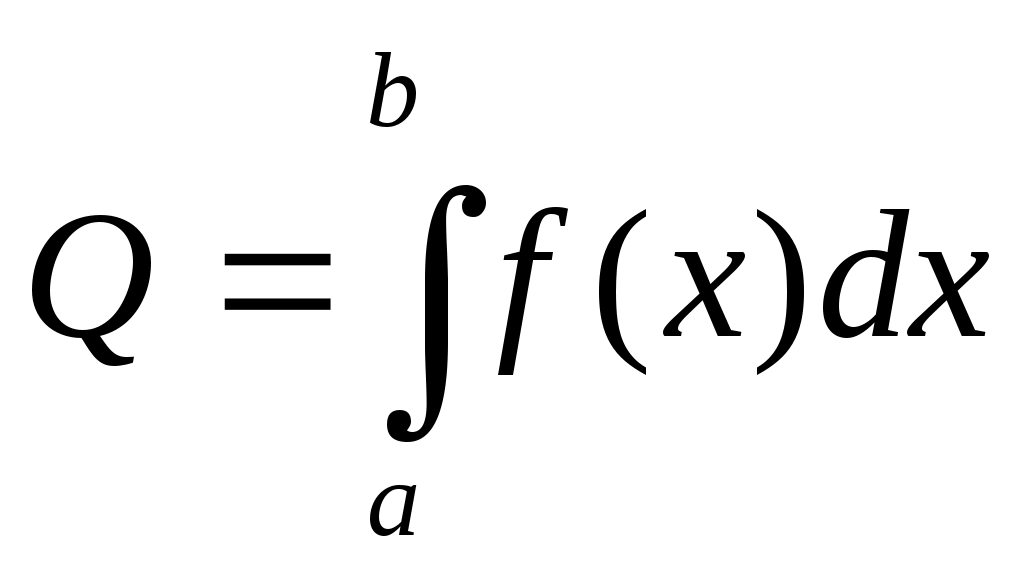
Q
|
№
|
Чертеж
|
Система координат и пояснения
|
Формула
|
Q
|
S,
п
л
ощ
а
д
ь
п
л
о
с
к
о
й
ф
и
г
у
р
ы
D
|
1
|
|
Д. С. К.
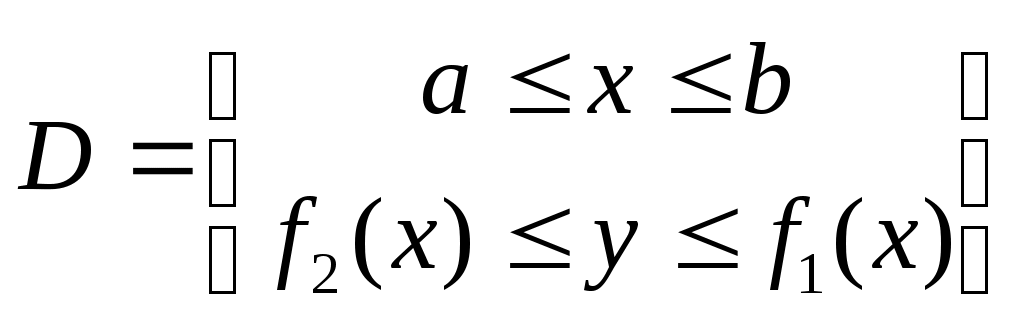
Одна кривая границы области Dне выше другой.
|
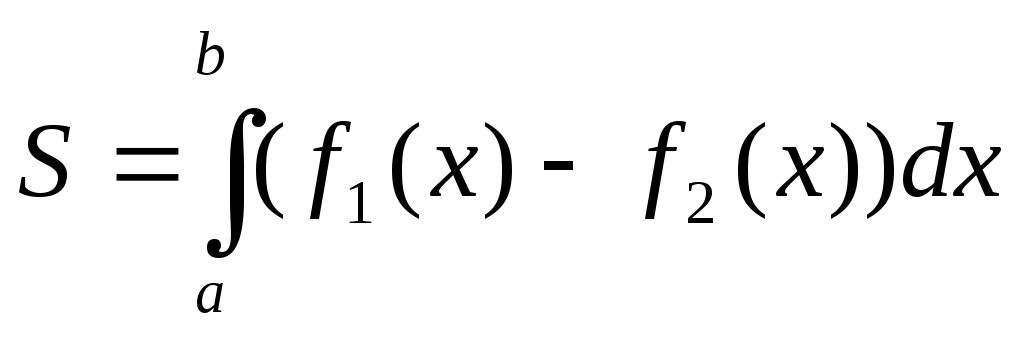
|
S,
п
л
о
щ
а
д
ь
п
л
о
с
к
о
й
ф
и
г
у
р
ы
D
|
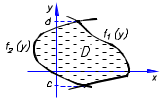
2
|
|
Д. С. К.
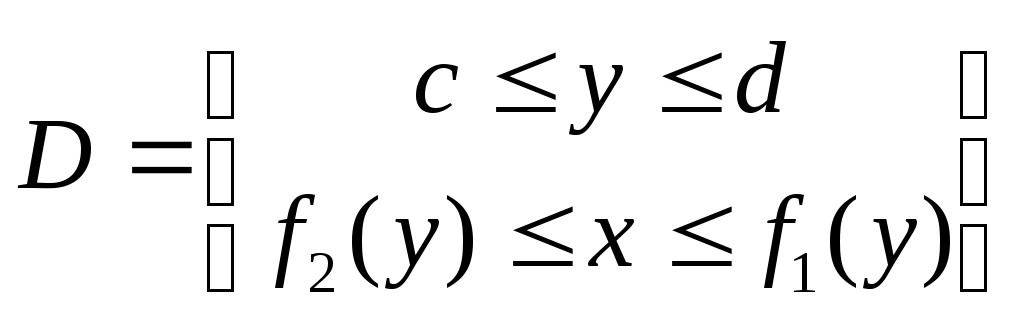
Одна кривая границы области Dне левее другой.
|
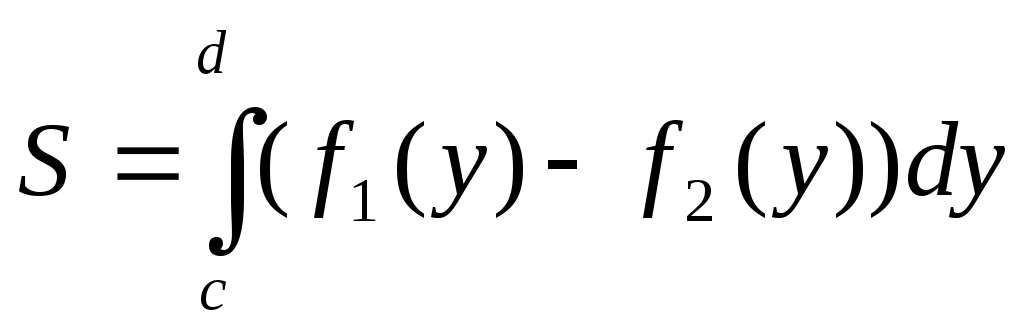
|
3
|
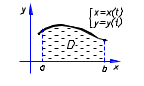
|
Д. С. К.
t
x()=a, x()=b
( y(t)0, t [, ] )
Верхняя граница области задана параметрически
|
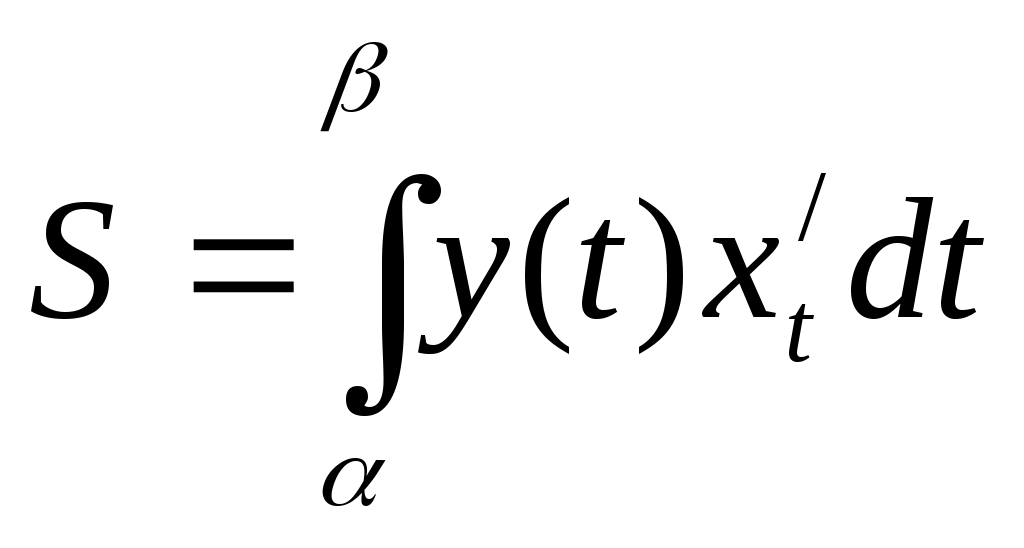
|
4
|

α
β
ρ1(φ)
ρ2(φ)
|
П. С. К.
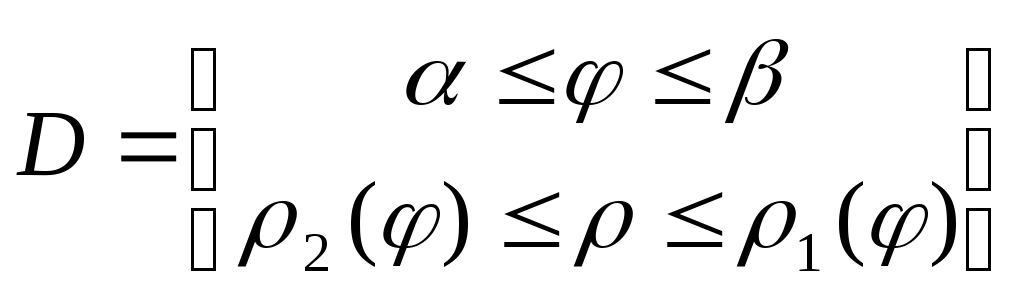
|
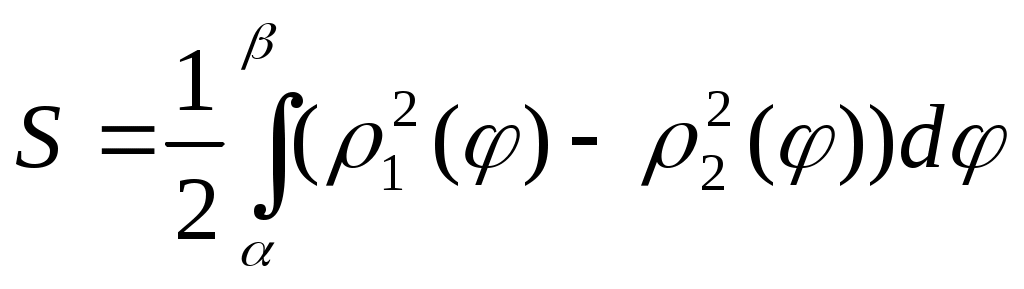
|
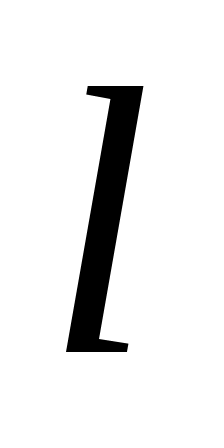 , ,
д
л
и
н
а
к
р
и
в
о
й
L
|
1
|
|
Д. С. К.
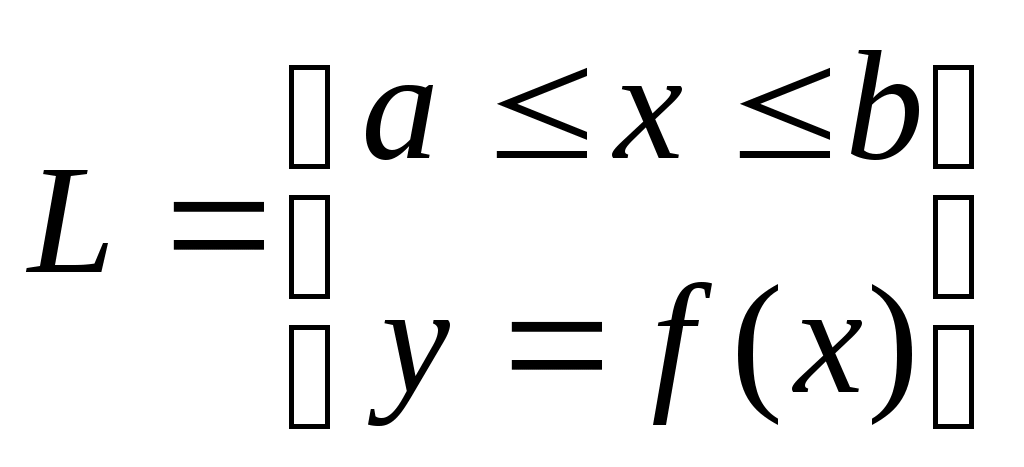
|
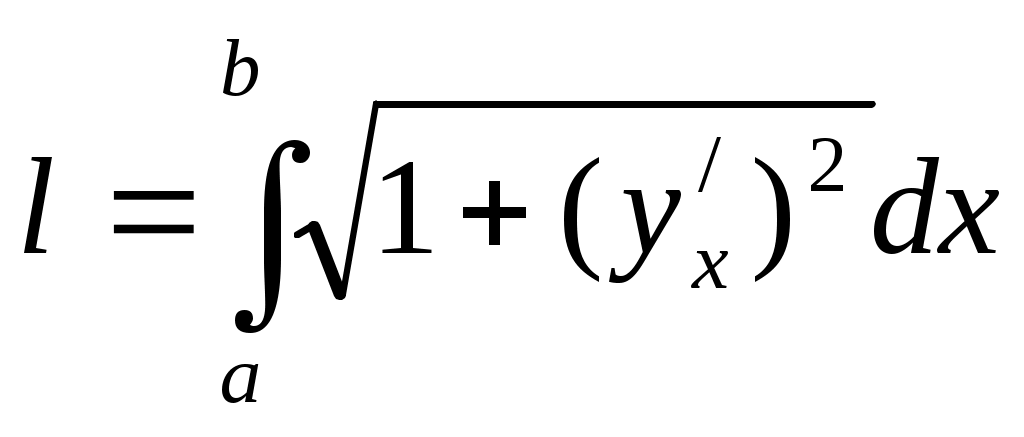
|
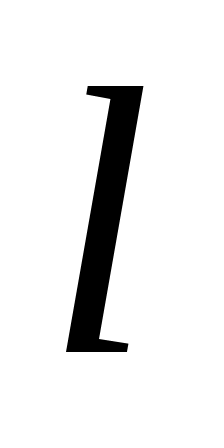 , ,
д
л
и
н
а
к
р
и
в
о
й
L
|
2
|
Д. С. К.
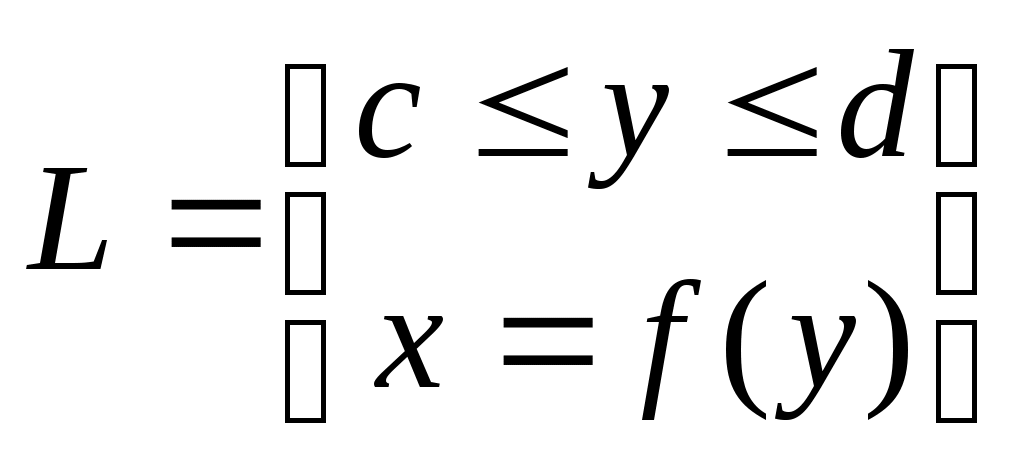
|
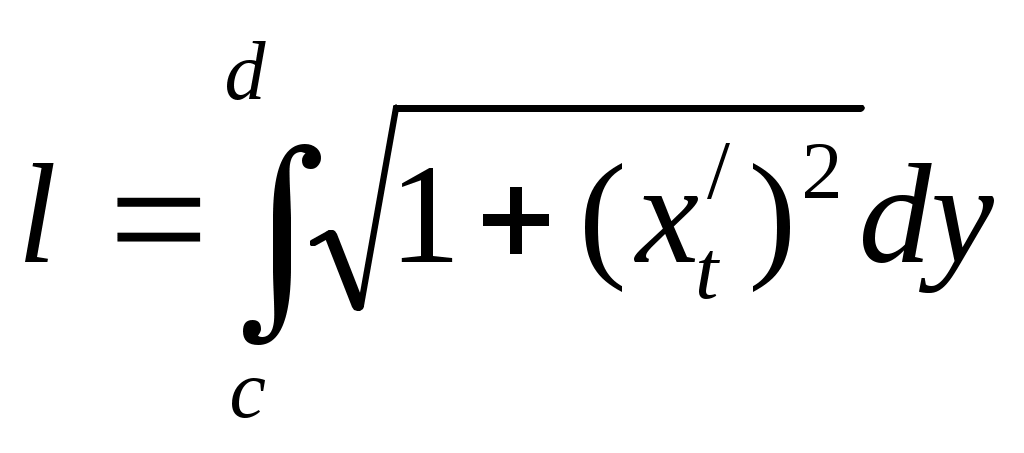
|
3
|
|
Д. С. К.
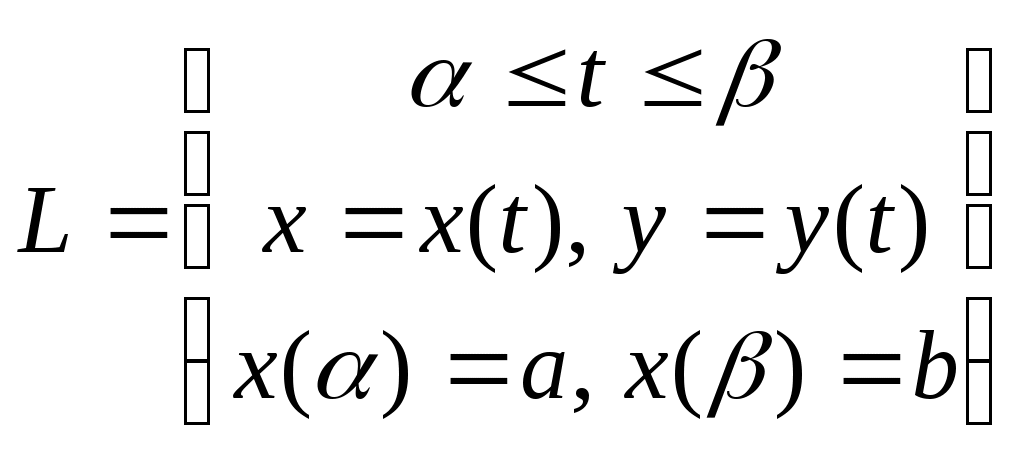
Линия L задана параметрически
|
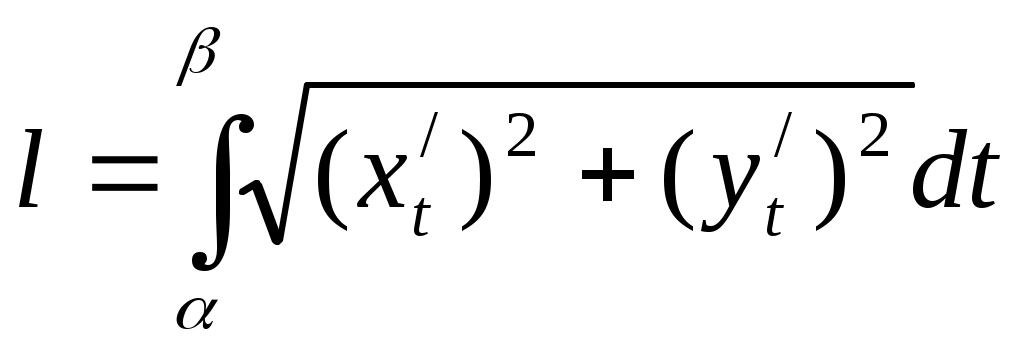
|
4
|

ρ(φ)
β
α
|
П. С. К.
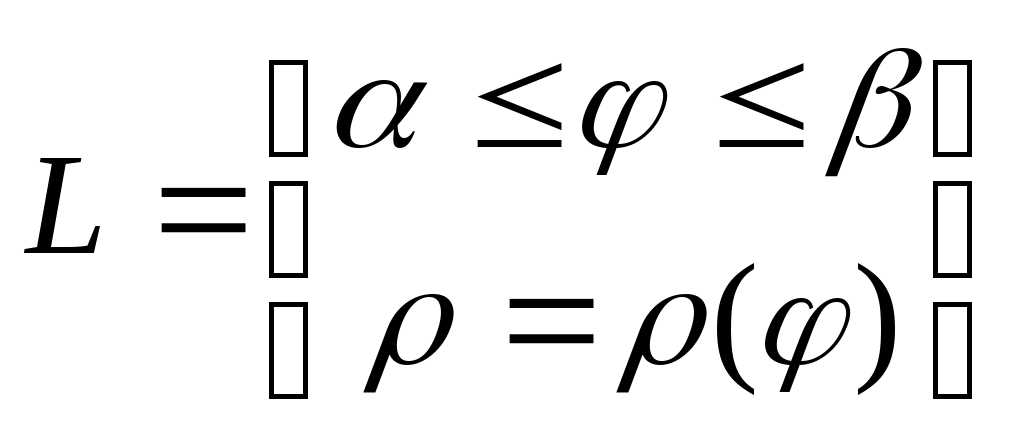
|
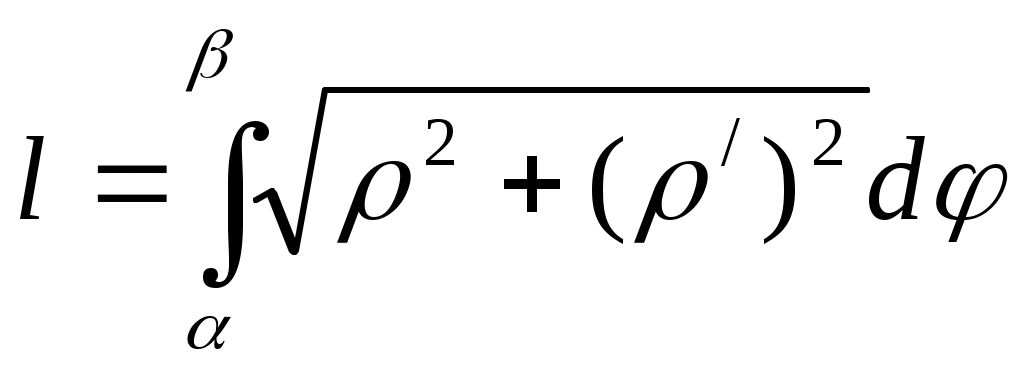
|
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Q |
№
|
Чертеж
|
Система координат и пояснения
|
Формула
|
Q
|
V,
о
б
ъ
е
м
т
е
л
а
Т
|
1
|
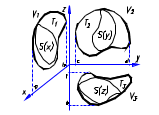
|
Д. С. К.
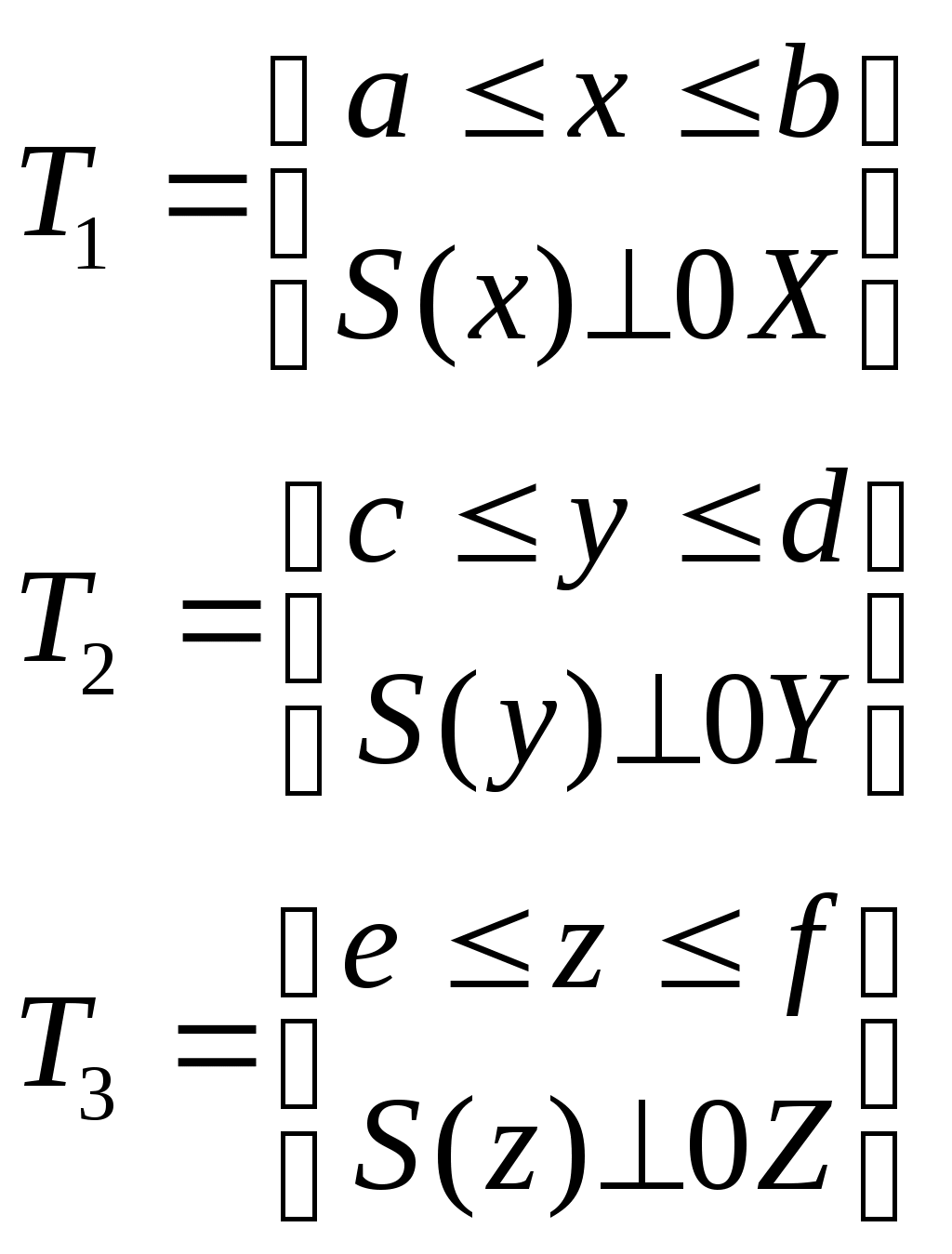
|
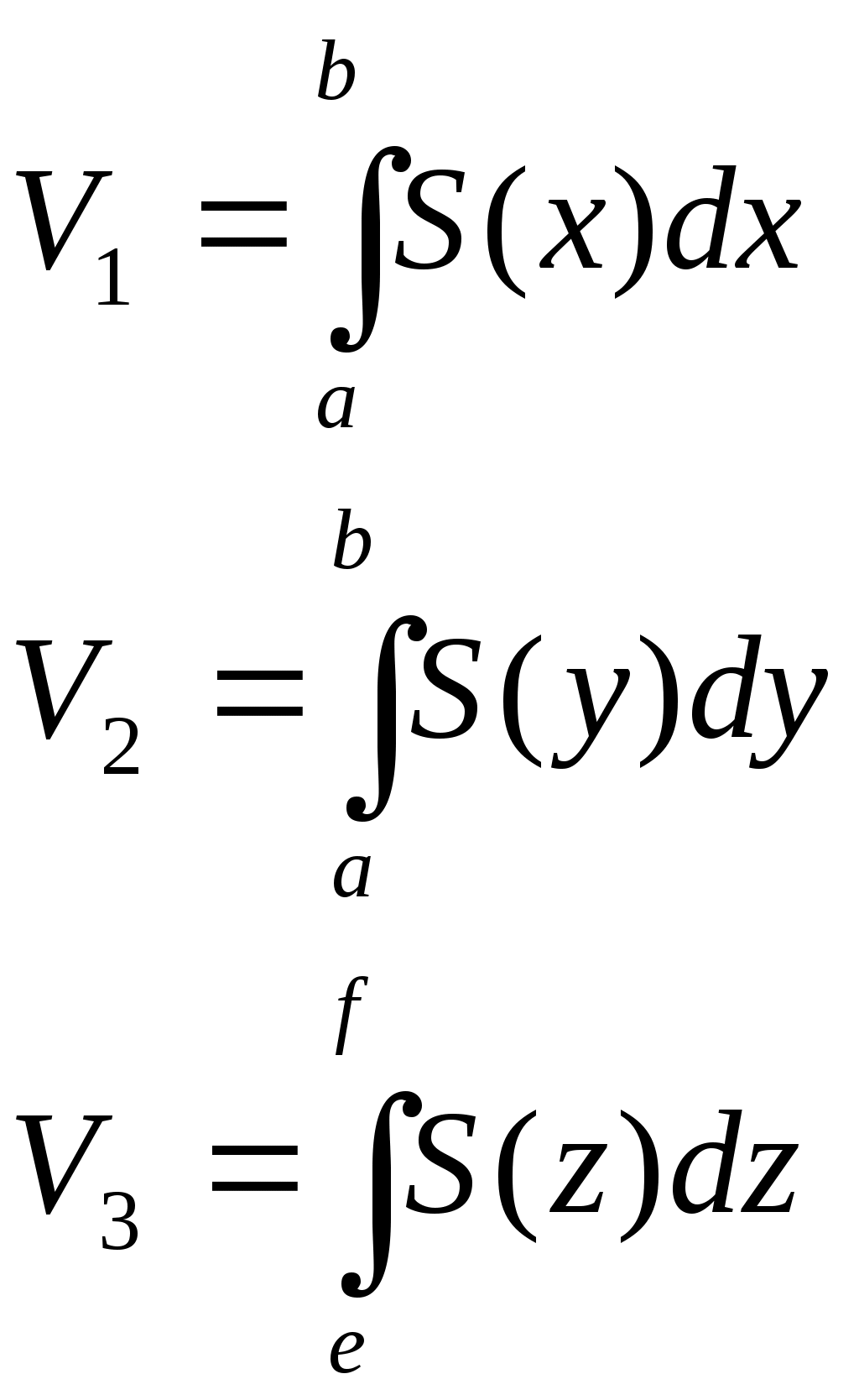
|
V,
о
б
ъ
е
м
т
е
л
а
Т
|
2
|
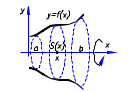
|
Д. С. К.
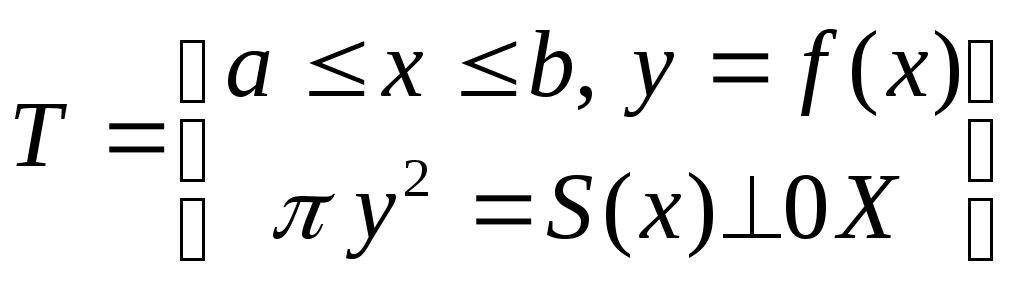
Тело Т образовано вращением кривой у=f(х) вокруг оси 0Х
|
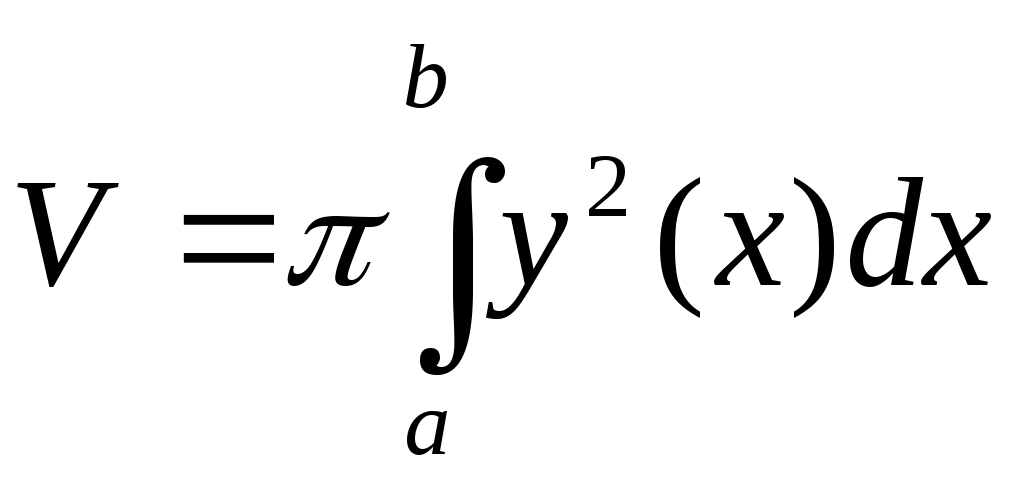
|
,
п
л
ощ
а
д
ь
п
о
в
е
р
х
н.
ω
|
1
|
|
Д. С. К.
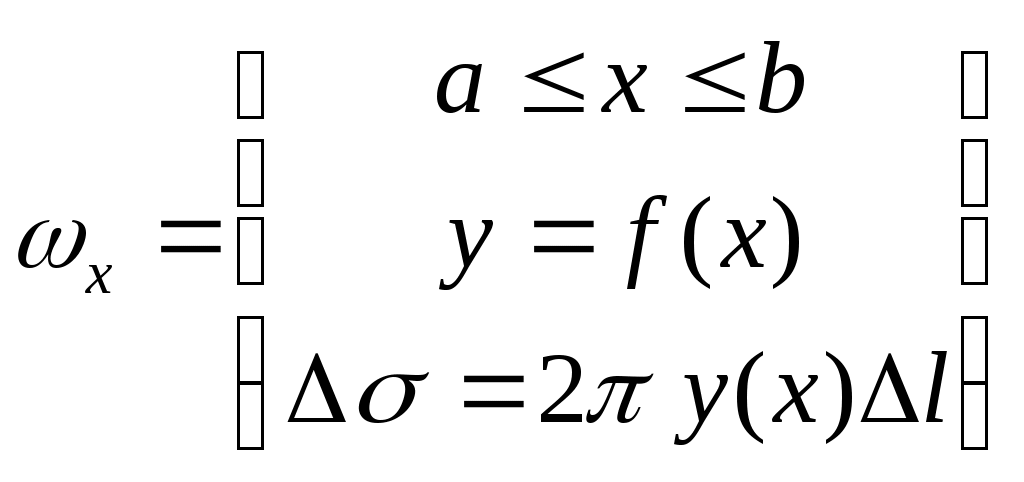
Поверхность образована вращением кривой у=f(х) вокруг оси 0Х
|
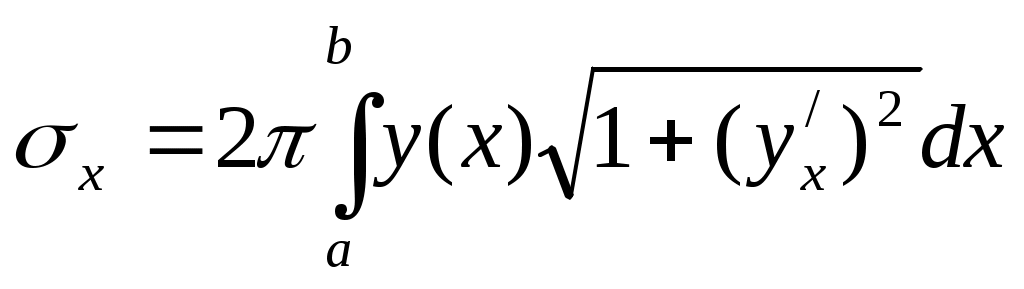
|
,
п
л
о
щ
а
д
ь
п
о
в
е
р
х
н.
|
Д. С. К.
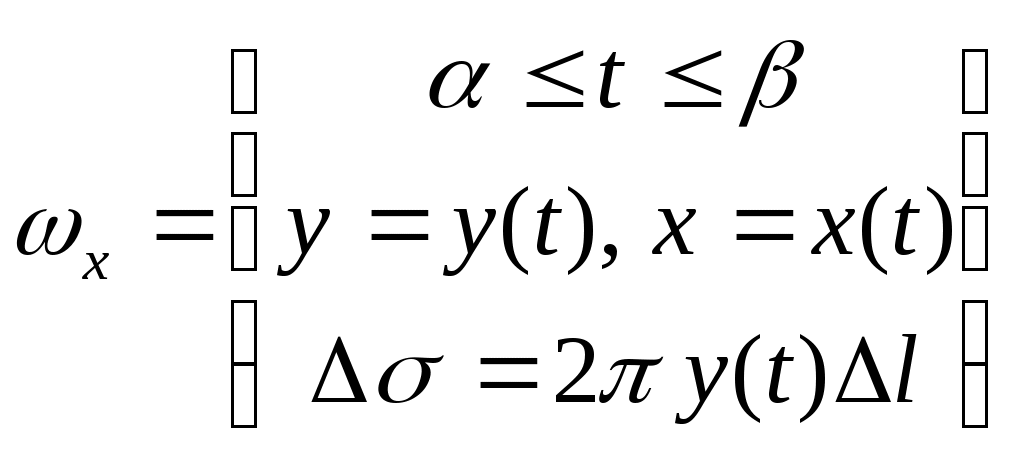
Поверхность образована вращением кривой у=f(х (t)), заданной параметрически, вокруг оси 0Х
|
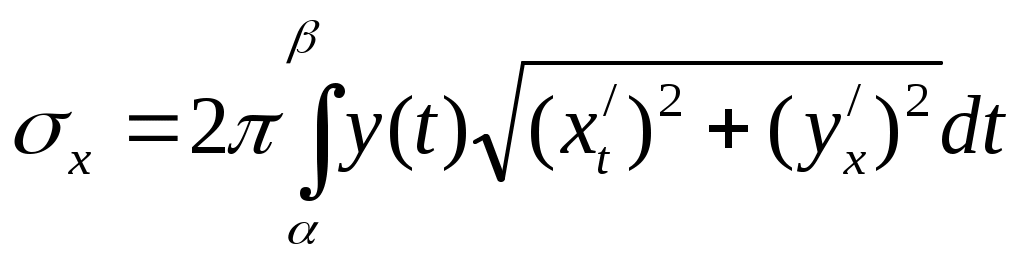
|
S,
п
у
т
ь
|
1
|
|
Д. С. К.
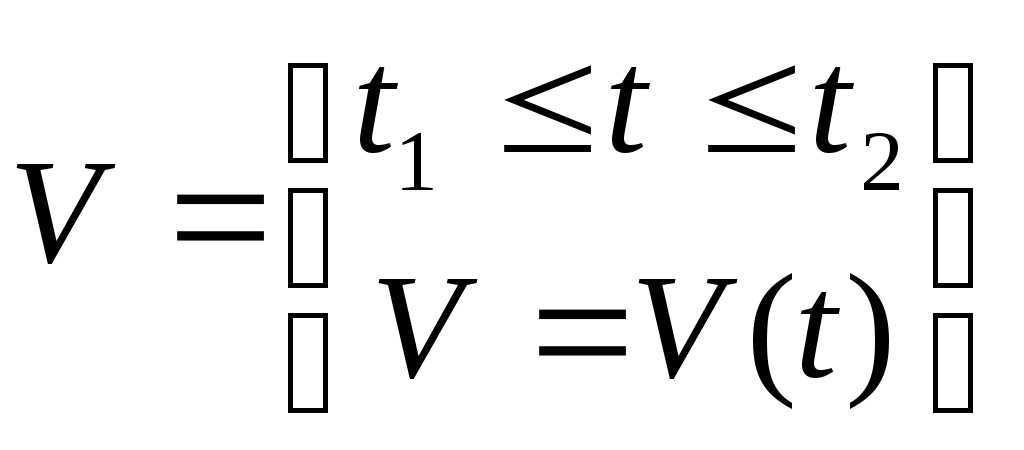
V – скорость прямолинейного движения тела на промежутке времени [t1,t2]
|
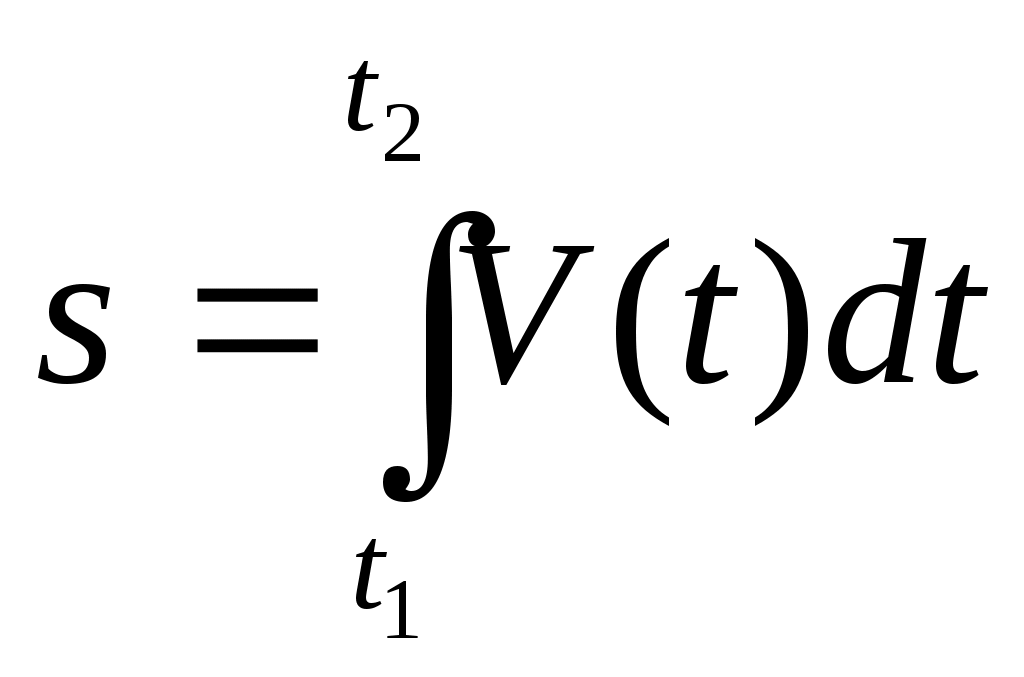
|
S,
п
у
т
ь
|
А,
р
а
б
о
т
а
|
1
|
|
Д. С. К.
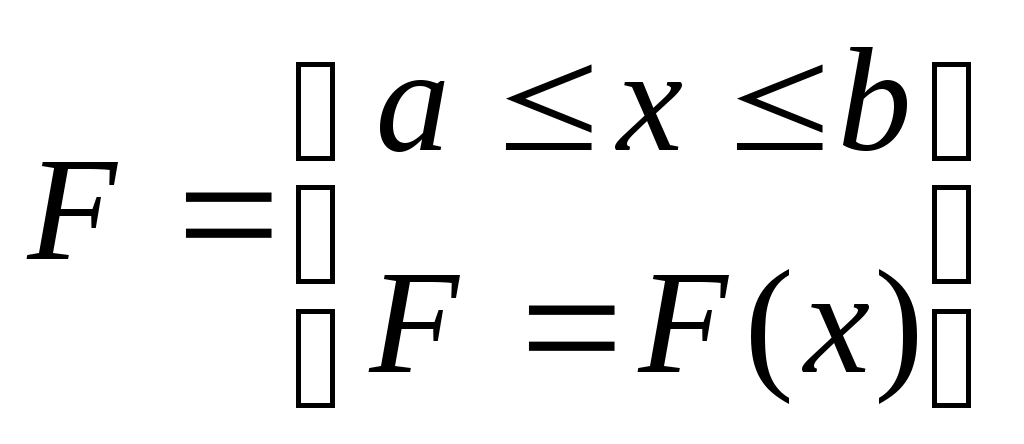
Сила F направлена параллельно оси 0Х на промежутке [a,b]
|
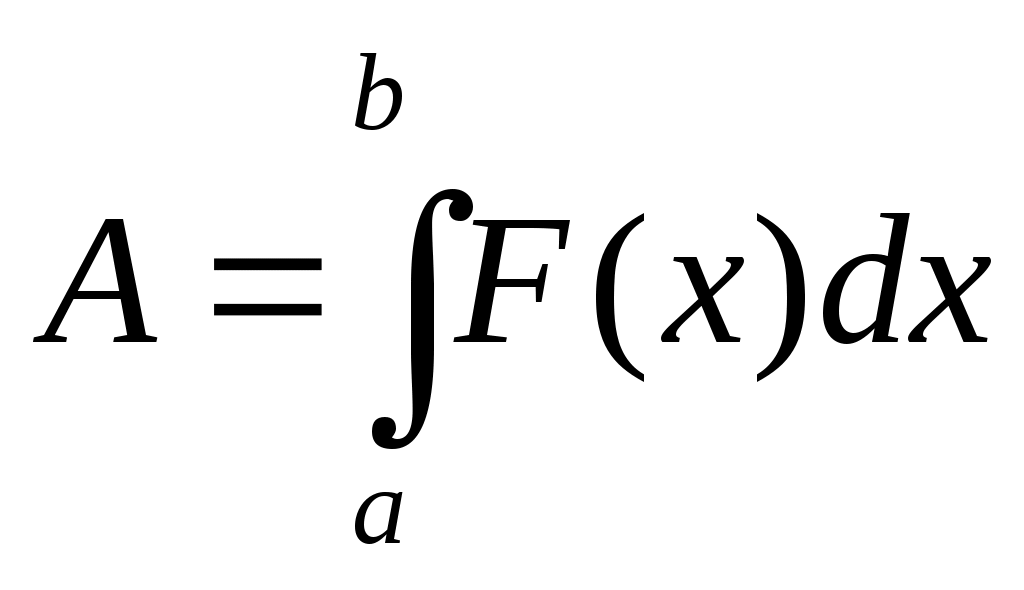
|
А,
р
а
б
о
т
а
|
Р,д
а
в
л
|
1
|
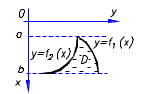
|
Д. С. К.
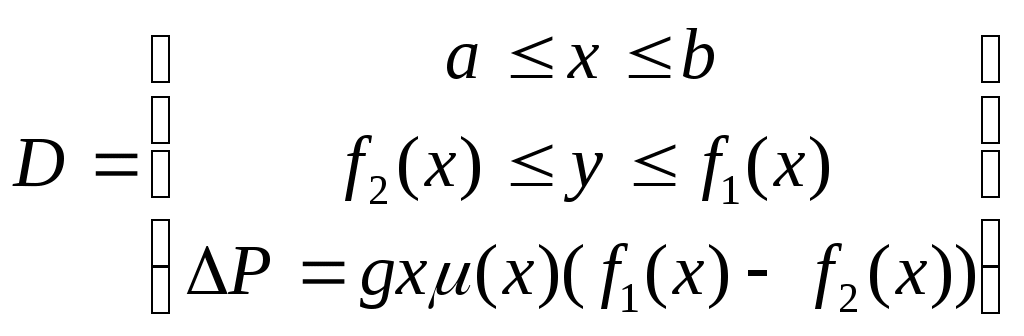
– плотность жидкости, давящей на пластину D
|
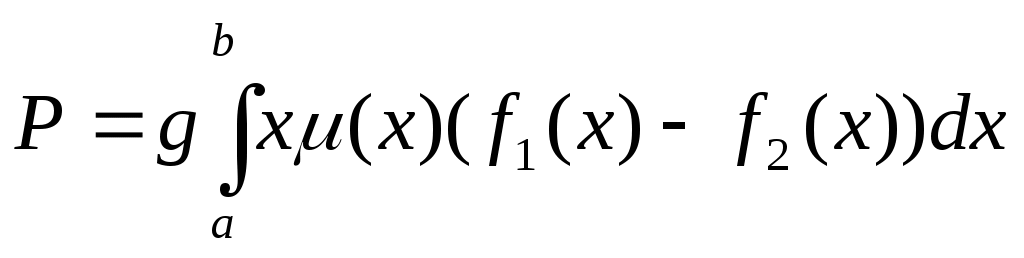
|
Р,
д
а
в
л.
|
m,м
а
с
с
а
|
1
|
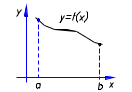
|
Д. С. К.
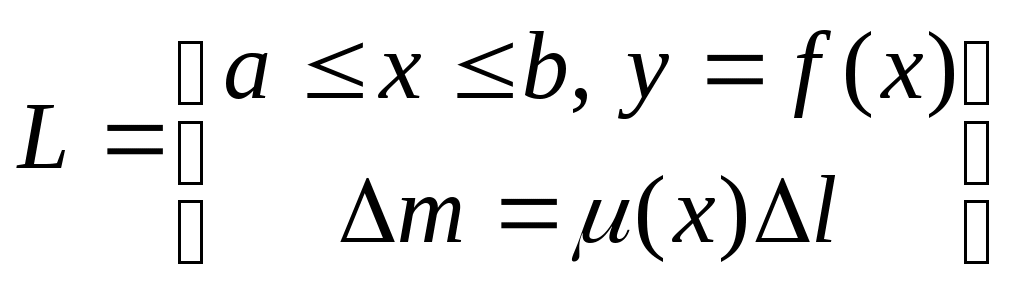
– линейная плотность кривой L
|
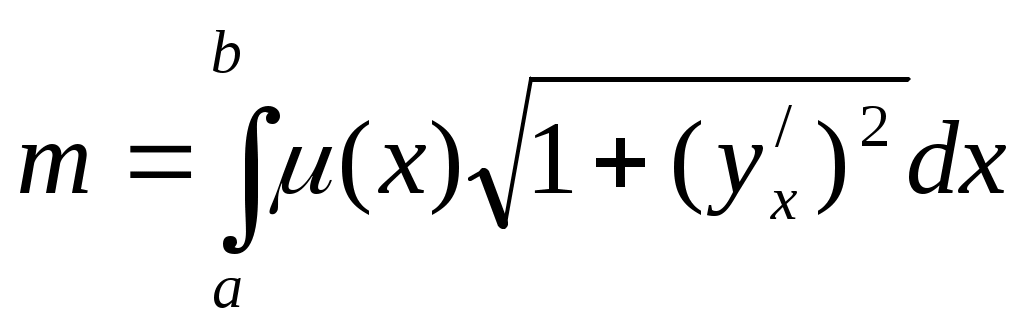
|
m,м
а
с
с
а
|
Статические моменты относительно координатных осей Sx, Sy,, моменты инерции Мх,, Му, координаты центра тяжести хс, ус плоской кривой
ОПРЕДЕЛЕНИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
|
Определенный интеграл
|
|
MR1
:{x[a,b]}
отрезок оси ОХ
|
Мi
|
=x
Mi=ixi
|
Определение, обозначение интеграла
|
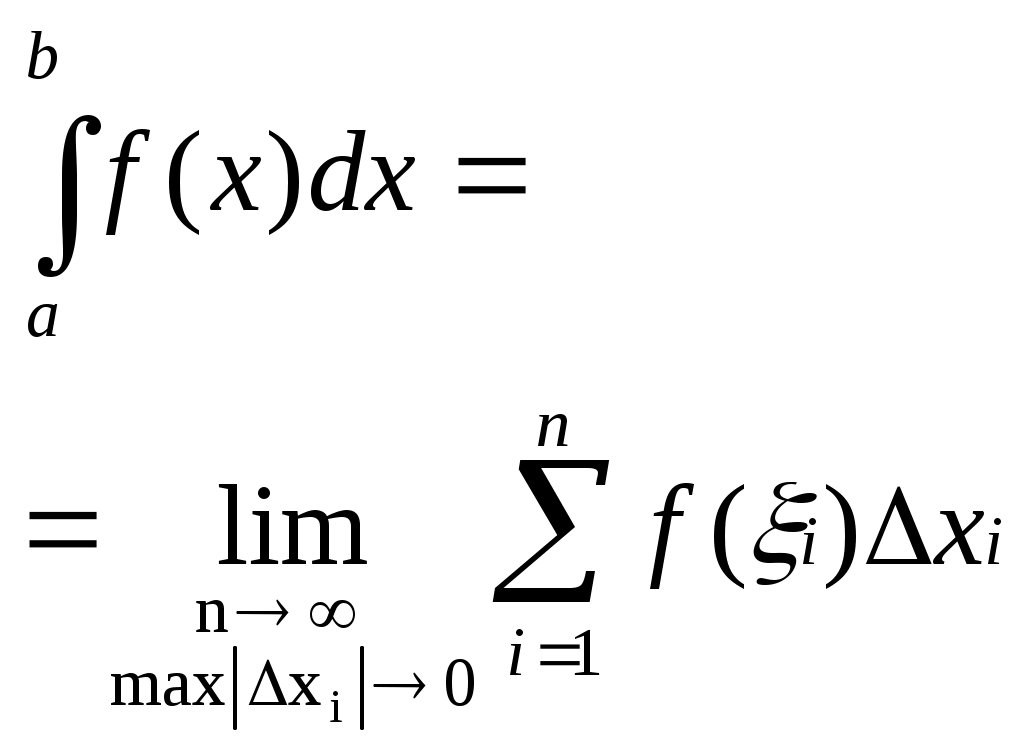
|
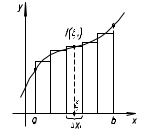
 Геометрический смысл. Геометрический смысл.
|
S – площадь криволинейной трапеции
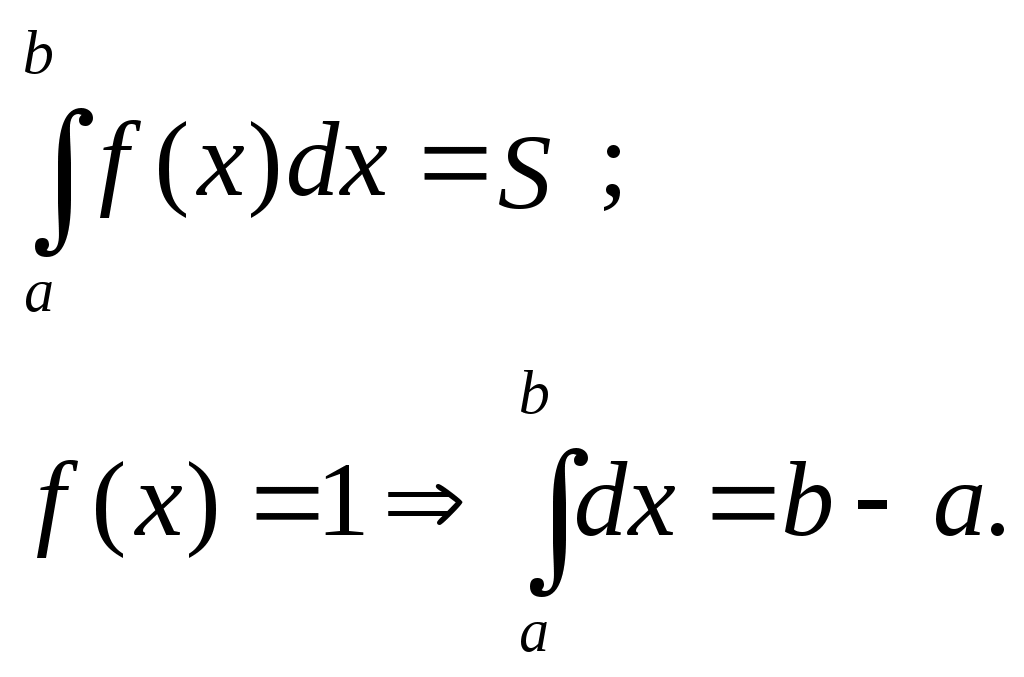
| |
|
|
 Скачать 264 Kb.
Скачать 264 Kb.