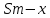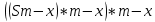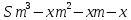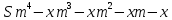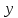ультра вариант. УВ. А Решение Пусть cl общая касательная двух окружностей, причём точки l и в лежат по одну сторону от прямой ас
 Скачать 81.59 Kb. Скачать 81.59 Kb.
|
|
УВ-4 13)     | :2 | :2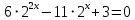 Замена      Выполним обратную замену   б) Найдём все корни принадлежащие отрезку от  В силу неравенств 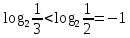 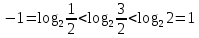  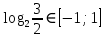 Подсказки: Подсказки: 1) Представь 4 в виде  и воспользуйся свойством возведения степени в степень и воспользуйся свойством возведения степени в степень 3) Представь концы отрезков в виде логарифмов и выполни сравнение 14) 59152 15)   Распишем аргумент второго логарифма и заметим, что его можно свернуть по формуле сокращенного умножения Распишем аргумент второго логарифма и заметим, что его можно свернуть по формуле сокращенного умножения  Теперь рассмотрим ОДЗ данного уравнения  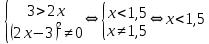 Вынесем 6 из основания первого логарифма, а из аргумента второго логарифма вынесем 2  Так как по ОДЗ Так как по ОДЗ    Перенесём всё влево и вынесем общий логарифм за скобочку Перенесём всё влево и вынесем общий логарифм за скобочку Применим метод рационализации Применим метод рационализации  Умножим левую и правую часть уравнения на 6 Умножим левую и правую часть уравнения на 6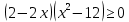 Из первой скобочки вынесем -2, а вторую распишем по формуле разности квадратов Из первой скобочки вынесем -2, а вторую распишем по формуле разности квадратов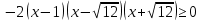  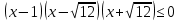  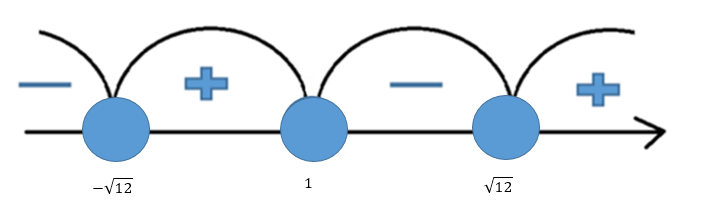 При условии ОДЗ запишем ответ  1  6) 6) а) Решение : Пусть CL — общая касательная двух окружностей, причём точки L и В лежат по одну сторону от прямой АС. Тогда по теореме об угле между касательной и хордой 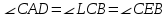 Значит, прямые AD и BE параллельны, поскольку соответственные углы CAD и СЕВ равны. б) Поскольку угол АСВ прямой, AD и BE — диаметры меньшей и большей окружностей соответственно. Прямоугольные треугольники ACD и ЕСВ подобны по острому углу (  ) )с коэффициентом подобия 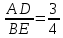 Пусть АС = ВС = x, тогда  В прямоугольном треугольнике ACD: 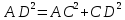 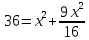 откуда.  Ответ: 4,8 17. Пусть S 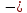 сумма кредита сумма кредита  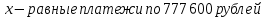 Погасим кредит за 4 года, тогда распишем историю кредита
Если долг выплачен 4 равными платежами х, то 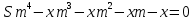 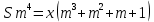 Теперь погасим кредит за 2 года, тогда распишем историю кредита у – равные платежи по 1 317 600 рублей
 Если долг выплачен 4 равными платежами х, то  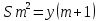 Тогда получим систему Тогда получим систему Подставим 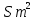 в первое уравнение и получим в первое уравнение и получим  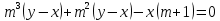    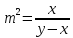 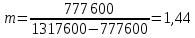 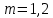   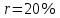 Ответ: Ответ:  18. Найдите все значения a, при каждом из которых уравнение  имеет ровно один корень на отрезке [0; 1]. имеет ровно один корень на отрезке [0; 1].Решение: Перенесём всё налево и вынесем общий множитель за скобочку     |