ИДЗ Интегралы с проверкой. Задача. Проверка
 Скачать 72.94 Kb. Скачать 72.94 Kb.
|
 Задача 1. Задача 1. 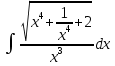 . .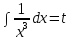 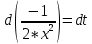 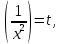 Множитель Множитель 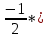 вынесем за знак дифферинциала. Заметим, что раз x∈ ℝ, то вынесем за знак дифферинциала. Заметим, что раз x∈ ℝ, то 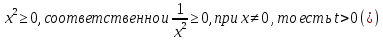 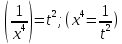 ; Множитель ; Множитель 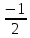 вынесем за скобки, но чтобы его не писать всё время посчитаем чему равен интеграл вынесем за скобки, но чтобы его не писать всё время посчитаем чему равен интеграл 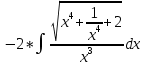 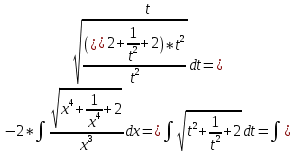 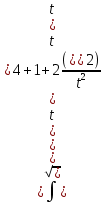 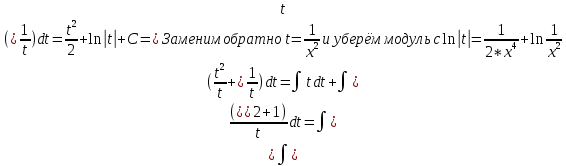 + C + C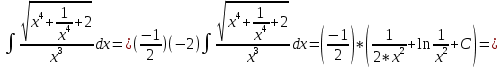  + + 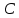 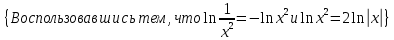 Проверка: ( 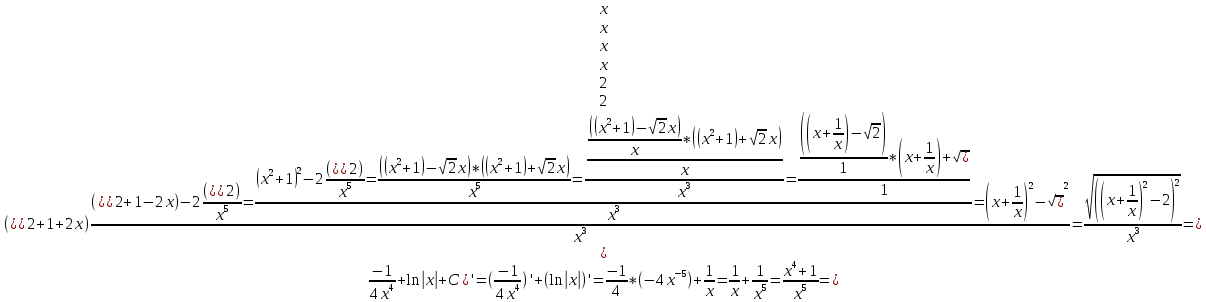 = 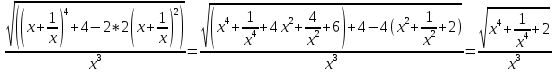 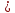 читд, получили исходную подынтегральную функцию читд, получили исходную подынтегральную функциюОтвет: 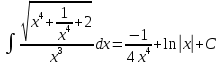  +1-1 Задача 2. 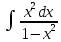 . .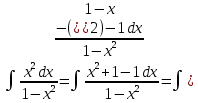 = = 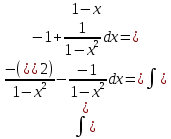 = 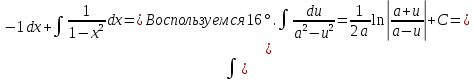 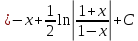 Проверка: 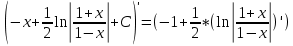 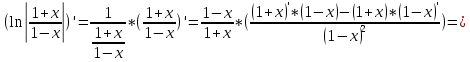 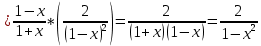 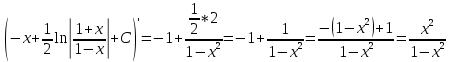 , что и является изначальной подынтегральной функцией (функции) , что и является изначальной подынтегральной функцией (функции)Ответ: . 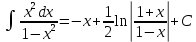  1 = 1 ^ 3 Задача 3. 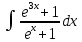 . .Заметим, что “1” – это и 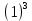 , А также отметим, что , А также отметим, что 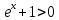 , т.к. , т.к. 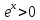 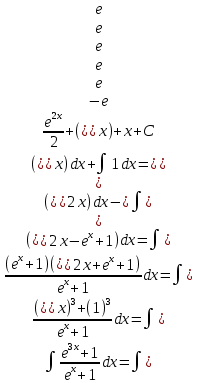 Проверка: 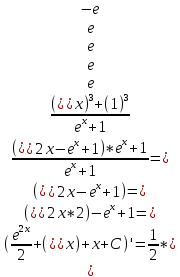 Что и является исходно подынтегральной функцией Ответ: 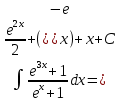   Задача 4. ∫(2x – 3)10 dx. Задача 4. ∫(2x – 3)10 dx.Пусть d(f(x)) = ∫f(x)dx, тогда d(f(x)) = d(2x-3) => 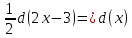 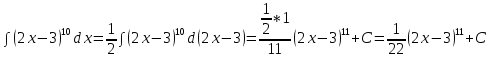 Проверка: 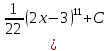 )’= )’=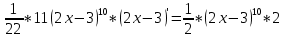 = =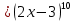 Что и является исходно подынтегральной функцией Ответ: 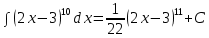  5x Задача 5. 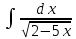 . .Пусть d(f(x)) = ∫f(x)dx, тогда d(f(x)) = d(2-5x) => 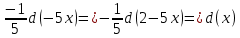 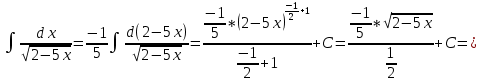 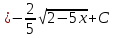 Проверка: 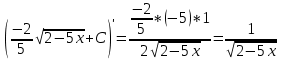 Получили функцию, равную той, что была в подынтегральном выражении Ответ: . 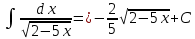 Задача 6. 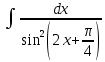 . .Пусть d(f(x)) = ∫f(x)dx, тогда d(f(x)) = d(2x+ 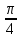 ) => ) => 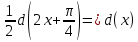 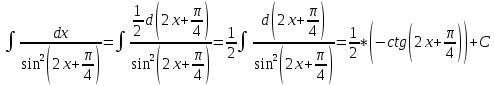 Проверка: 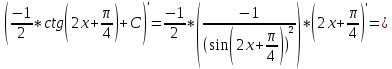 = 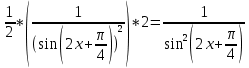 Получили функцию, равную той, что была в подынтегральном выражении Ответ: 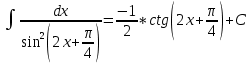 Задача 7. 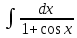 . .1 = 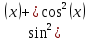   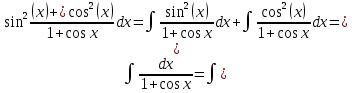 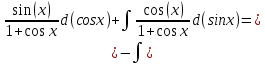 Ничего не “улучшилось”. Попробуем по-другому преобразовать подынтегральную функцию. Вспомним, что существует такое тождество   1+cos(2x) = 1+cos(2x) = 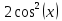 , тогда 1+cos(x) = , тогда 1+cos(x) = 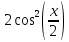 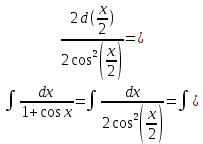 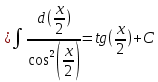 Проверка: 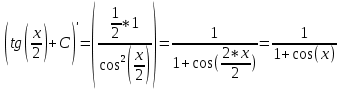 Совпадение с исходной подынтегральной функцией Ответ: 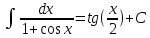   Задача 8. Задача 8. 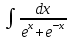 . .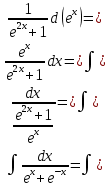 Так как 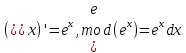 Заменим 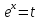 И воспользуемся формулой 15°. 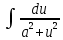 = = 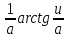 + C. + C.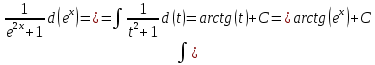 Проверка: 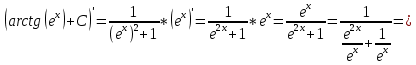 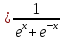 Что совпадает с исходной подынтегральной функцией Ответ: 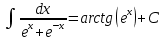 ИДЗ-1-2Вариант-Пример-1 Дано: 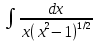 Пусть 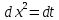 , тогда , тогда 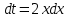 , тогда , тогда 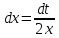 , t= , t=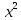 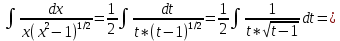 Попробуем ещё замену: 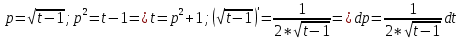 Найдём этот член 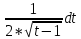 в интеграле: в интеграле:   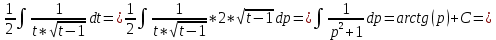 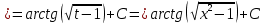 Проверка: 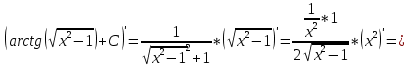 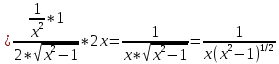 Что и является подынтегральной функцией Ответ: : 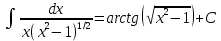 ИДЗ-1-2Вариант-Пример-2 Решить:  Вспомним, что (   Разделим интеграл на два “попроще” 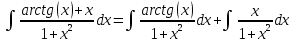 Тогда Воспользовавшись (*) Получим: 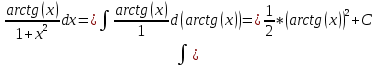 (**) (**)Теперь решим правую часть суммы интегралов (2) 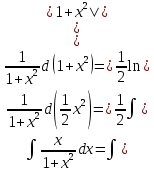 +C +CПросуммируем (3) и (4), а также отметим, что 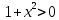 , x∈ ℝ , x∈ ℝ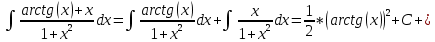 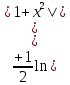 Проверка: 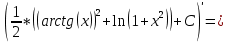 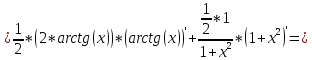 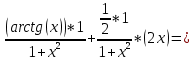 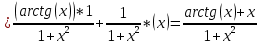 Подынтегральные функции при проверке совпали Ответ: : 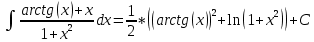 Проверим, например, такое тождество (из “Таблица основных интегралов (ТИ)”): 17°. 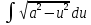 = = 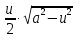 + + 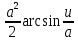 + C + CНайдём производную подынтегральной функции 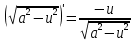 Преобразуем подынтегральную функцию в что-то подобное основного тригонометрического тождества 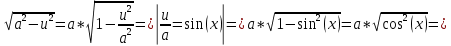 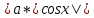 (*) (*)Выглядит так, что что-то улучшилось. Теперь нужно воспользоваться 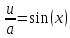 И вычислить dx:  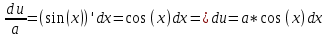 (**) (**)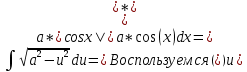 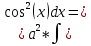 Воспользуемся формулой понижения степени косинуса 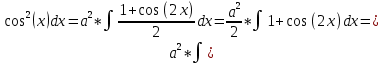 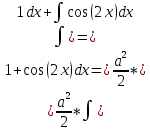 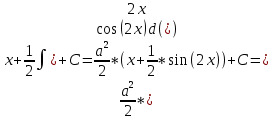 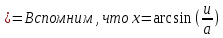 == ==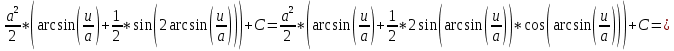 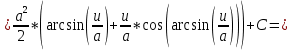 Есть такая формула, выводящаяся из прямоугольного треугольника x = u/a 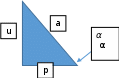 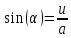 ; ; 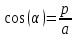 ; ; 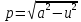 Тогда: 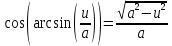 Конечно, из треугольника можно доказать только Для a>u Или вот так: 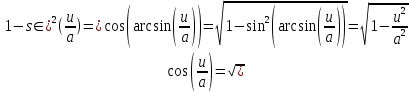 (***) (***) Вернёмся к нашему примеру Вернёмся к нашему примеру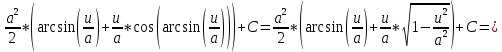 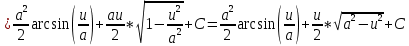 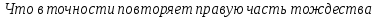 ЧИТД |
