Математика4 практ -. Занятие 4 Обучающийся Ершова Алина Александровна Преподаватель Галкина Людмила Сергеевна
 Скачать 86.5 Kb.
|
|
Автономная некоммерческая профессиональная образовательная организация «Национальный социально –педагогический колледж» Программа среднего профессионального образования 44.02.01 Дошкольное образование Дисциплина: Математика Практическое занятие №4 Выполнил: Обучающийся Ершова Алина Александровна Преподаватель: Галкина Людмила Сергеевна Контрольная работа 4 I. Найти значение других трех основных тригонометрических функций, если: а).  и  .В третьей четверти косинус отрицательный, а тангенс и котангенс - положительные. Из основного тригонометрического тождества получаем:  Далее по определению   б).  и  .Во второй четверти синус положительный, а тангенс и котангенс - отрицательные. Из основного тригонометрического тождества получаем:  Далее по определению   .Ответы: а).  ;  б).  ;  .II. Вычислите: а).  .Подставив значение 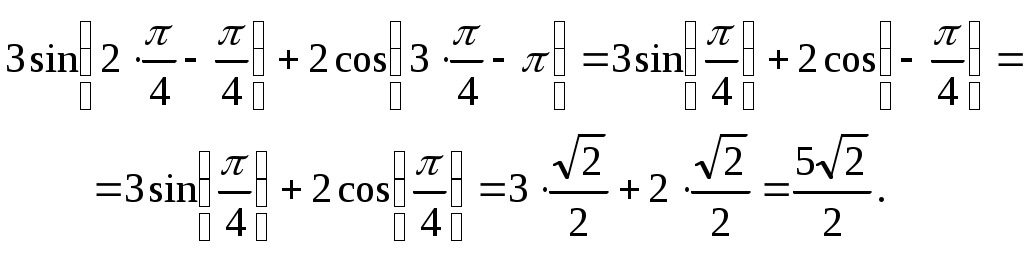 в данное выражение, получим: Учитываем четность косинуса и подставляем табличные значения тригонометрических функций. б).  .Подставив значение  в данное выражение, получим: Учитываем нечетность тангенса и подставляем табличные значения тригонометрических функций. Ответ: а).  ; б).  .III. Вычислите: а).  . Преобразуем данное выражение, применяя формулы приведения, используя четность и нечетность тригонометрических функций, и подставим табличные значения тригонометрических функций нужных аргументов. 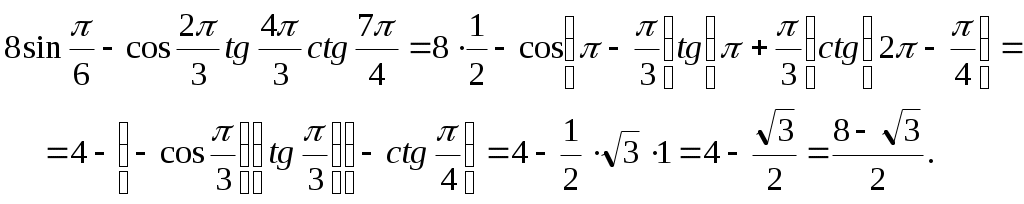 б).  .Преобразуем данное выражение, применяя формулы приведения, используя четность и нечетность тригонометрических функций, и подставим табличные значения тригонометрических функций нужных аргументов. 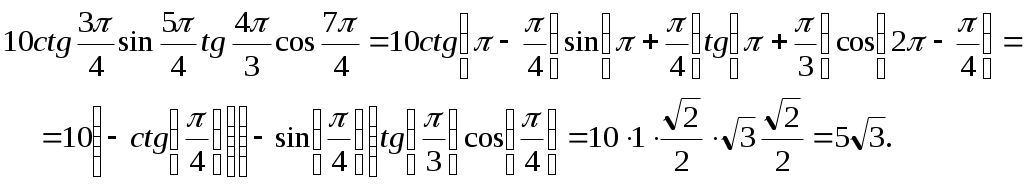 Ответ: а).  ; б).  . |