Лекция на тему Формулы приведения. Урок 37. Формулы приведения. Перечень вопросов, рассматриваемых в теме формулы приведения

• Название: Урок 37. Формулы приведения. Перечень вопросов, рассматриваемых в теме формулы приведения
• Дата: 11.04.2023
• Размер: 254.5 Kb.
• Имя файла: Лекция на тему Формулы приведения .docx
• Тип: Урок; #1053897

Урок 37. Формулы приведения

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №37. Формулы приведения.

Перечень вопросов, рассматриваемых в теме:

• 
  формулы приведения;
  
• 
  мнемоническое правило для формул приведения;
  
• 
  преобразование тригонометрических выражений на основе использования формул приведения;
  
• 
  вычисление значений тригонометрических выражений на основе формул приведения;
  
• 
  доказательство тригонометрические тождества на основе формул приведения;
  
• 
  решение уравнения с использованием формул приведения.
  

Глоссарий по теме

Формулы приведения – это формулы, которые позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.

Теоретический материал для самостоятельного изучения

Для вычисления углов больше 90  используют формулы приведения. Они позволяют синус, косинус, тангенс и котангенс различных углов приводить к острым углам.

Пример: Вычислить   и .

Представим число  .

Рассмотрим точку А(1;0) на единичной окружности. При повороте вокруг начала координат на угол   она сделает 2 полных оборота   и ещё повернётся на угол  . Переместится в точку В, в которую могла бы попасть, сделав поворот на угол  . Значит,  ,  .

А так как  , то  ,

Количество полных оборотов по 360  или по   может выражаться любым целым числом k, как положительным, так и отрицательным и нулём. При повороте точки А(1;0) на угол  , где k  получается та же самая точка, что при повороте на угол 

Рисунок 1 – точки А и В на единичной окружности

Справедливы равенства:

, где  ,  , где

Пусть точка А(1;0) переместилась в точку В₁ при повороте на угол   и в точку В при повороте на угол  (рис. 2).



Рисунок 2 – точки А, В, В1 на единичной окружности

Запишем   в виде:  . На единичной окружности точки В₁ и В симметричны относительно оси Оу, значит их ординаты (синусы) равны, абсциссы (косинусы)- противоположные числа.

Поэтому  , а  .

А так как  , то  ,  .

Помним, что  , тогда  ,  .

Докажем, что для всех углов  справедливы формулы:

,  .

Воспользуемся формулой синуса и косинуса разности: , подставим известные значения   в формулу, получаем:

.

 (1)



 (2)

Аналогично доказываются формулы:

 (3)

 (4)

 (5)

 (6)

 (7)

 (8)

 (9)

 (10)

 (11)

 (12)

Эти формулы называются формулами приведения для синуса и косинуса.

Пример: вычислите  . Представим  , тогда  .

Выведем формулы для тангенса, используя его определение

 ,

Найдём 



 



Получаем формулы для тангенса и котангенса:

, где   и  , где   (13)

 (14)

 (15)

 (16)

 (17)

Пример: вычислите  .

Преобразуем выражение в скобке 

.

Обратите внимание, что все эти формулы связывают синусы с синусами или косинусами, а тангенсы с тангенсами или котангенсами. В одних случаях синус меняется на косинус и наоборот, в других – нет. Так, например, в формулах 1,2,3,8 и 13, где в левой части присутствуют   синусы, косинусы и тангенсы не меняются.

В остальных формулах, где в левой части присутствуют  или  , синус меняется на косинус и наоборот, а тангенс на котангенс.

Формул приведений много и их не обязательно каждый раз выводить и запоминать.

Для этого придумали мнемоническое правило.

1. 
   Если в левой части присутствуют   и т.д. синусы, косинусы и тангенсы не меняются.
   

Если в левой части присутствуют   или  , синус меняется на косинус, косинус на синус, тангенс на котангенс.

1. 
   Знак в правой части ставим тот же, который имело исходное число в левой части, при условии   .
   

Существует легенда про рассеянного математика, который всё время забывал менять или не менять синус на косинус и наоборот. Он смотрел на свою сообразительную лошадь и она кивала головой вдоль той оси, где стояли числа  и  ,  . (рис. 3)



Рисунок 3 – «правило лошади»

Если аргумент содержал  или  , лошадь кивала вдоль оси Оу. Это означало «да, менять». А если  , кивала вдоль оси Ох – «не менять».

Так же помните: чётные числа вида  и т.д. находятся на оси Ох справа от нуля на единичной окружности, а нечётные   и т. д. слева от нуля.

Если в выражении перед   стоит плюс, то точка перемещается по окружности по часовой стрелке, если стоит минус, то против часовой стрелке.

Примеры и разбор решения заданий тренировочного модуля

Пример 1: упростите выражение  .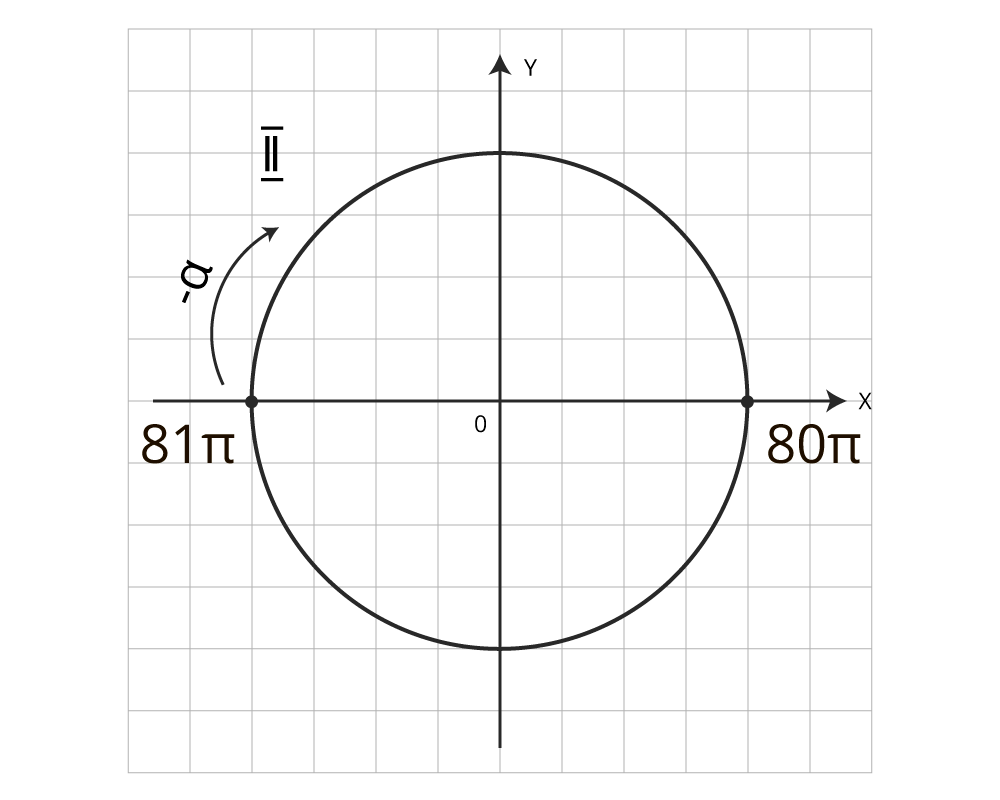

 находится на оси Ох, слева от нуля, косинус не меняем. Перед   минус, точка перемещается против часовой стрелке и попадает во вторую четверть, здесь косинусы отрицательные (рис.4)



Рисунок 4 – перемещение точки по единичной окружности

Значит  = .

Пример 2: вычислите 

Преобразуем выражение в скобке:  .   находится слева на оси Ох, синус не меняем. Угол в третьей четверти, синусы отрицательные.