Главная страница
Навигация по странице:

  • Тип урока

  • Ход урока Организационный момент

  • Актуализация знаний

  • Изучение нового материала

  • Закрепление изученного материала .

  • Домашнее задание.

    		•

    План урока Алгебра 8 класс Значение синуса, косинуса и тангенса для углов 30°, 45°, 60°. ПОур Алг 8 кл Значения sin cos. Геометрия Урока Класс. 8 Тема урока Значение синуса, косинуса и тангенса для углов 30, 45, 60 Цель образовательная


    Скачать 49.79 Kb.
    НазваниеГеометрия Урока Класс. 8 Тема урока Значение синуса, косинуса и тангенса для углов 30, 45, 60 Цель образовательная
    АнкорПлан урока Алгебра 8 класс Значение синуса, косинуса и тангенса для углов 30°, 45°, 60
    Дата09.04.2022
    Размер49.79 Kb.
    Формат файлаdocx
    Имя файлаПОур Алг 8 кл Значения sin cos.docx
    ТипУрок
    #456523

    Дата: _____________ Предмет. Геометрия № Урока_________ Класс. 8

    Тема урока: Значение синуса, косинуса и тангенса для углов 30°, 45°, 60°
    Цель:-образовательная:

    формирование у учащихся умений вычислять значения синуса, косинуса и тангенса для углов 30˚, 45˚, 60˚. Способствовать формированию навыков решения прямоугольных треугольников, используя синус, косинуса и тангенса острого угла, составить таблицу значений для синуса, косинуса и тангенса.

    -развивающая:

    развитие логического мышления, памяти, внимания, интереса к предмету, формирование умения анализировать, сопоставлять данные, выводить логические следствия из данных предпосылок, умение делать выводы.

    -воспитательная:

    воспитание у учащихся аккуратности, ответственное отношение к учению, культуру общения.

    Тип урока: урок усвоения новых знаний.

    План урока:

    1. Организационный момент (1 минута)

    2. Актуализация знаний (5 минут)

    3. Изучение нового материала (15 минут)

    4. Закрепление нового материала (15 минут)

    5. Рефлексия (3 минуты)

    6. Домашнее задание (1 минута)

    Ход урока

    1. Организационный момент

    Включает в себя приветствие учителем класса, проверку готовности кабинета к проведению урока, проверку отсутствующих.

    1. Актуализация знаний

    Учитель: Сегодня на уроке мы вычислим значения синуса, косинуса и тангенса для углов 30°, 45°, 60°, научимся применять полученные значения при решении задач. (Слайд 1)

    Учитель: Итак, проверим домашнее задание. Начнем с проверки теоретических вопросов.

    Учитель: Для начала давайте вспомним с Вами, что называется синусом острого угла прямоугольного треугольника? (Слайд 2)

    Ученик: Отношение противолежащего катета к гипотенузе.

    Учитель: Что называется косинусом острого угла прямоугольного треугольника? (Слайд 3)

    Ученик: Отношение прилежащего катета к гипотенузе.

    Учитель: Что называется тангенсом острого угла прямоугольного треугольника? (Слайд 4)

    Ученик: Отношение противолежащего катета к прилежащему катету.

    Учитель: Назовите основное тригонометрическое тождество. (Слайд 5)

    Ученик:

    Учитель: Чему равен тангенс угла? (Слайд 5)

    Ученик: Отношению синуса к косинусу этого угла.

    Учитель: Теперь перейдем к проверке домашнего задания №591 (б, в)?

    Ученик: б) sin⦟A=cos⦟В= , cos⦟A=sin⦟B= , tg⦟A= , tg⦟B= .

    в) sin⦟A=cos⦟В= , cos⦟A=sin⦟B=, tg⦟A= , tg⦟B= 2

    Учитель: Верно

    1. Изучение нового материала

    Запись на доске и в тетрадях:

    число…

    Классная работа.

    Тема «Значения синуса, косинуса и тангенса для углов 30˚, 45˚, 60˚»

    Учитель: Найдем сначала значения синуса, косинуса и тангенса для углов 30˚и 60˚. (Слайд 7)

    1)Рассмотрим прямоугольный треугольник ∆ABC с прямым углом С, у которого =30˚, =60˚. Нарисуйте у себя в тетрадях (ученики рисуют)

    Дано: ∆ABC,=30˚, =60˚.

    Найти: sin30˚,cos30˚,tg30˚, sin 60˚,cos 60˚, tg 60.
    Решение

    1. (по 2 свойству прямоугольного треугольника)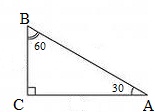




    Ответ:sin30˚= , cos 60˚=

    1) Давайте вспомним свойства прямоугольных треугольников, чему равен катет, лежащий против угла в 30˚? (половине гипотенузы)

    Тогда чему равно отношение ?

    2) Верно. А теперь посмотрите на рисунок, какому углу равно отношение ?

    (sin A=sin 30˚ и cos B=cos 60˚)

    3) Итак, sin30˚=  и cos 60˚=.

    4) Воспользуемся основным тригонометрическим тождеством и выразим cos и sin . Чему они будут равны?

    Подставим значения и посчитаем чему равен cos 30˚и sin 60˚.

    5) По какой формуле находим tg и tg ? Какому отношению он равен?

    Учитель: Найдем теперь sin45˚,cos 45˚ и tg45˚. Для этого рассмотрим равнобедренный прямоугольный треугольник АВС с прямым углом С.

    Нарисуйте у себя в тетрадях (ученики рисуют). (Слайд 8)

    Дано: ∆ABC ,АС=ВС, =45˚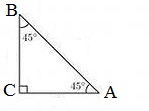

    Найти:

    sin45˚,cos 45˚, tg45.˚

    Решение

    1. АВ2=АС2+ВС2=2АС2=2ВС2 (по теореме Пифагора)

    2. АС=ВС=, то sin 45˚=sinA==

    3. cos 45˚=cosА==

    tg 45˚= tgA==1

    Ответ:sin 45˚=, cos 45˚=,tg=1

    1)По условию АС=ВС, =45˚.

    По теореме Пифагора найдем чему равна АС и ВС. Назовите мне теорему?

    (АВ2=АС2+ВС2)

    Верно, тогда можно записать, что АВ2=АС2+ВС2=2АС2=2ВС2.

    2)Чему отсюда равна АС и ВС?(АС=ВС= )

    Следовательно, мы можем посчитать sin 45˚ по формуле. (sinA= )

    Подставим найденные значения и выясним чему равен sin 45˚.(sin 45˚=sinA= )

    3) Найдем значения cos 45˚ и tg 45˚ по формулам. Какие формулы мы для этого используем?(cos А= и tgA=)

    Находим значения по данным формула. Чему они равны?

    (cos 45˚= cos А==и tg 45˚= tg A==1)

    Учитель: А теперь давайте заполним таблицу значений sinα, cosα, tgα для углов α, равных 30˚, 45˚, 60˚.(Слайд 9)

    1. Закрепление изученного материала.

    Учитель: Следующий номер №602. Стороны прямоугольника равны 3 см и см. Найдите углы, которые образует диагональ со сторонами прямоугольника.

    Запись на доске и в тетрадях:

    1. Проводим диагональ ВD и отмечаем углы.

    2. Что мы получили?

    (два прямоугольных треугольника)

    1. Рассмотрим ∆АВD, что нам известно?

    (АВ= , АD=3 и )

    1. Что мы можем выяснить, если известны два катета?(tg)

    1. Чему равен тангенс острого прямоугольного треугольника? (Отношению противолежащего катета, к прилежащему катету)

    2. Подставим известные значения, и находим tg=

    3. Посмотрите в таблице, чему равен tgα=?

    (60 градусам)- угол ВАС

    1. Зная , что мы можем найти?

    (угол ВСА= 90-60=30˚)

    Ответ: 60˚ и 30˚.
    Учитель: Решаем следующий номер, №599 (вызывает одного ученика к доске). Найдите площадь равнобедренной трапеции с основаниями 2 см 6 см, если угол при большем основании равен .

    Запись на доске и в тетрадях:

    Решение

    1. ∆АВВ1 =∆DСС1 , так как АВСD -равнобедренная трапеция.

    2. АВ1=С1D=(6-2):2=2см

    3. ∆АВВ1: ВВ1=АВ1*tgВВ1=2*tg

    4. SABCD=(AD+ВС)* ВВ1,

    SABCD=(6+2)* 2* tg=8tgсм2

    Ответ: 8tgсм2

    1. Проводим высоты и отмечаем буквами В1и С1.

    2. Что можно сказать о полученных ∆АВВ1 и ∆DСС1?

    (они равны, так как АВСD -равнобедренная трапеция).

    1. Что из этого следует?

    (АВ1=С1D=(6-2):2=2см)

    1. Рассмотрим ∆АВВ1. Что мы можем найти, если известен катет и угол?

    (сторону ВВ1=АВ1*tg ,

    ВВ1=2* tg)

    1. По какой формуле вычисляется площадь равнобедренной трапеции?(равна произведению полу суммы ее оснований на высоту)

    (SABCD=(AD+ВС)* ВВ1)

    1. Подставим известные значения, и находим площадь.

    1. Рефлексия .

    Учитель: Итак, ребята, сегодня на уроке мы с Вами нашли значения синуса, косинуса и тангенса для углов 30˚, 45˚, 60˚. Составили таблицу значений для этих углов. Давайте еще раз скажем, чему они равны, чтобы вы их лучше запомнили.

    Чему равен sinα для углов 30˚, 45˚, 60˚?

    Ученик: sin 30˚=, , , sin 45˚=.

    Учитель: чему будет равен cosα для углов 30˚, 45˚, 60˚?

    Ученик:cos 45˚=,cos 60˚=.

    Учитель: чему будет равен tgα для углов 30˚, 45˚, 60˚?.

    Ученик: ,tg45˚=1.

    Учитель:Молодцы.

    1. Домашнее задание. Изучить п.67. решить №603, выучить значения углов

    2. Итоги урока. Оценка и самооценка уч-ся на уроке

    написать администратору сайта