ряды фурье. Ряды.Ряды Фурье.Сборник задач. Сборник задач по высшей математике. РостовнаДону 2008г. 1
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
|
§4 Ряды Тейлора. Определение. Рядом Тейлора для функции 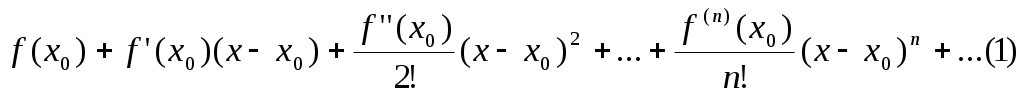 Обозначим 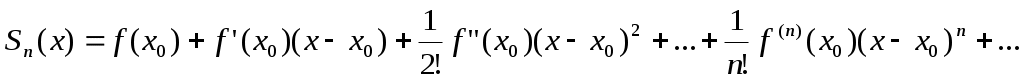 Ряд Тейлора функции Если ряд Тейлора в области сходимости имеет своей суммой Величина Для выяснения, стремится ли Теорема: Если функция Это остаточный член в форме Лагранжа. Для разложения данной функции в ряд Тейлора нужно 1) написать ряд Тейлора для данной функции, т.е. вычислить значения этой функции и ее производных при 2) Исследовать остаточный член Пример. Разложить в ряд Тейлора функции: 1) Решение: 1) Вычисляем значения данной функции и ее производных при 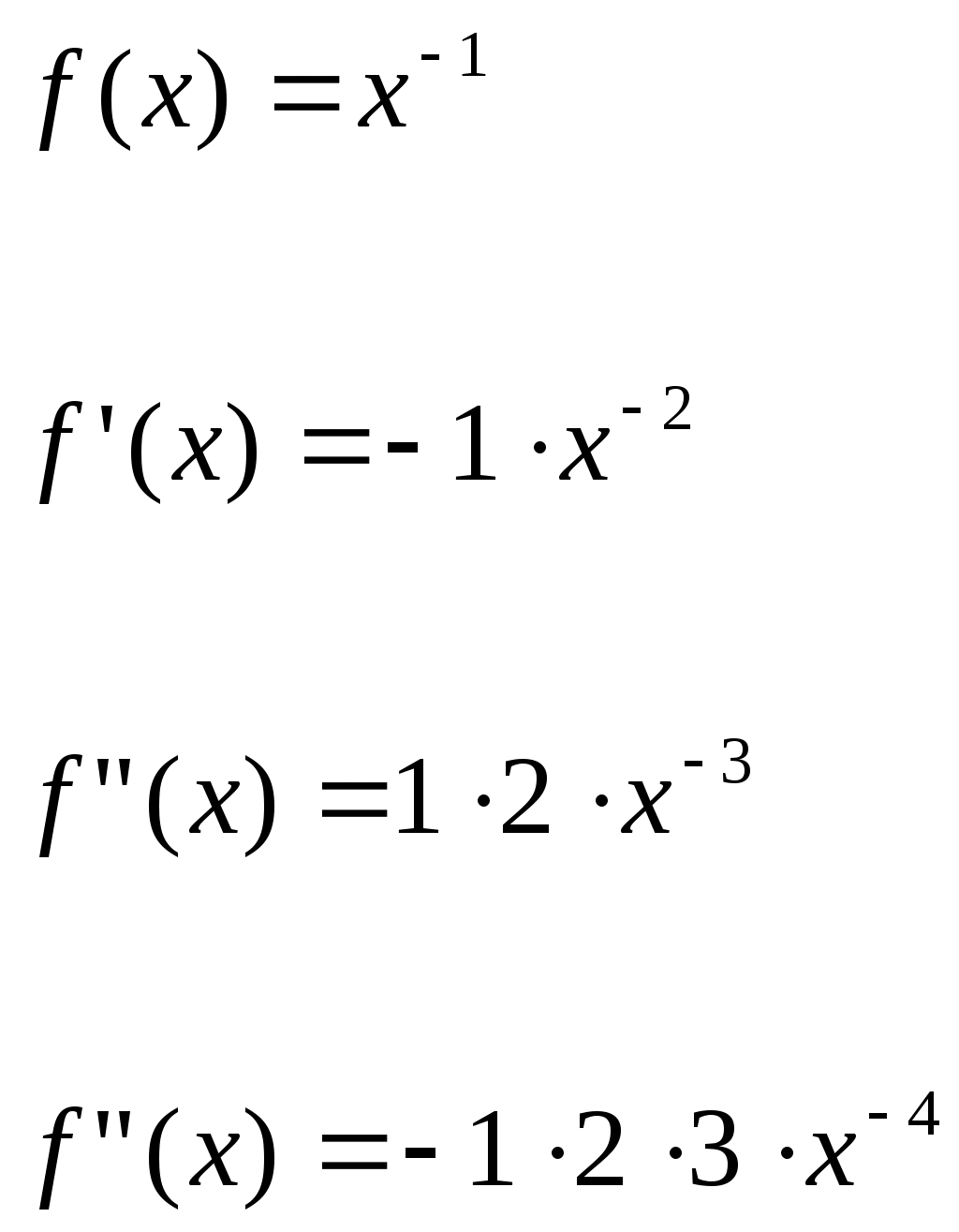 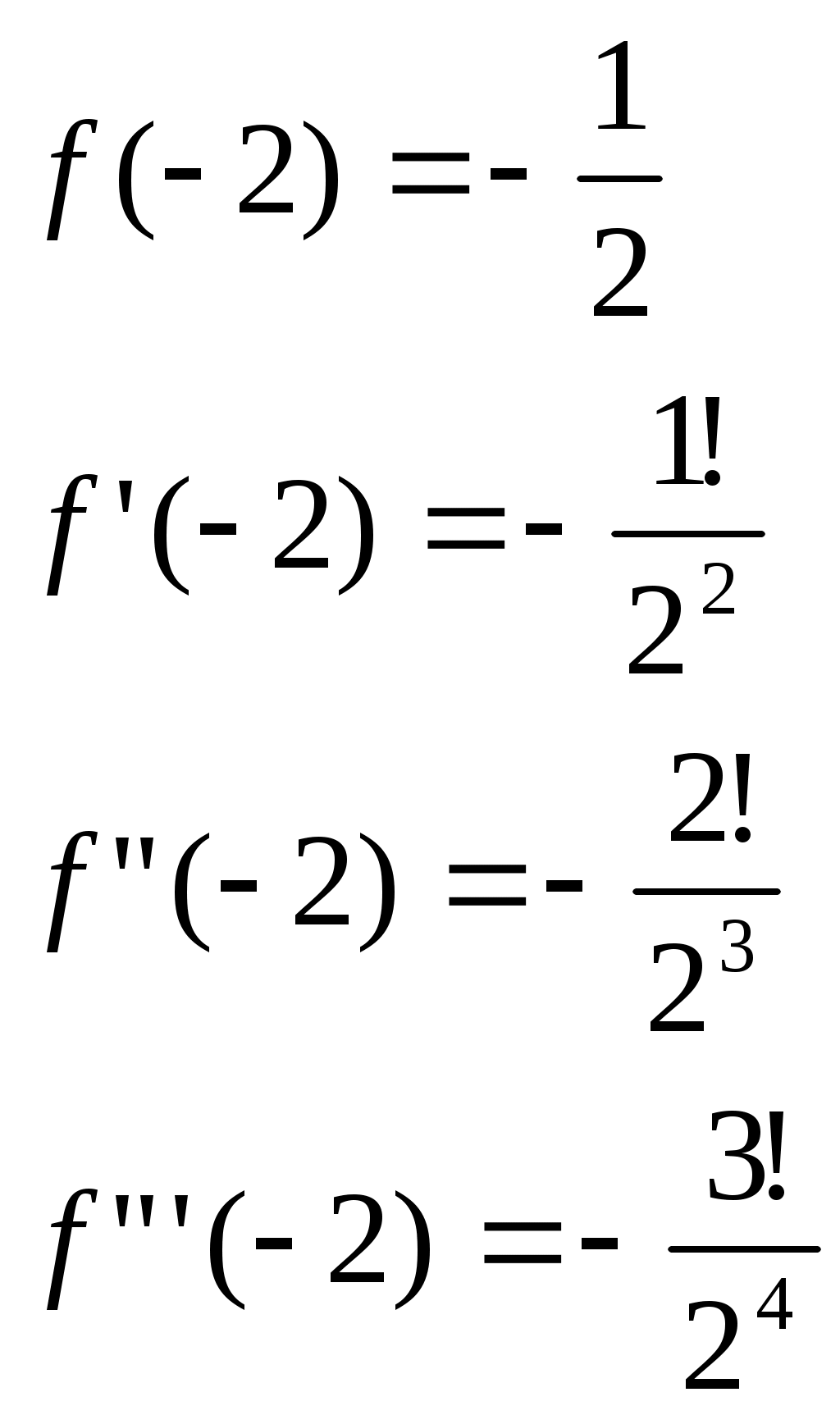 ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ Подставляем эти значения в ряд Тейлора (1) для произвольной функции, получим: 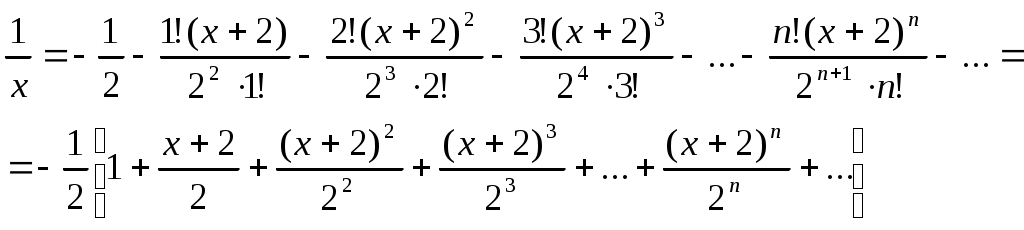 Исследуем сходимость полученного ряда по признаку Даламбера. Следовательно, интервал сходимости полученного ряда Тейлора для данной функции есть ( 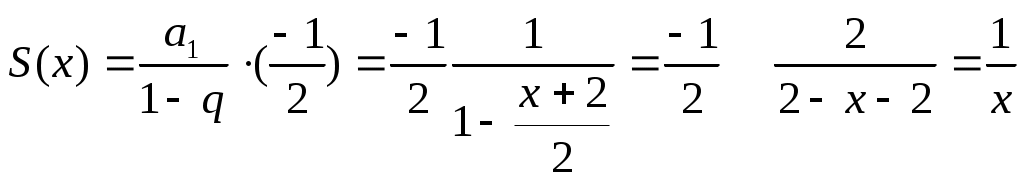 , , что доказывает сходимость ряда именно к данной функции. 2) 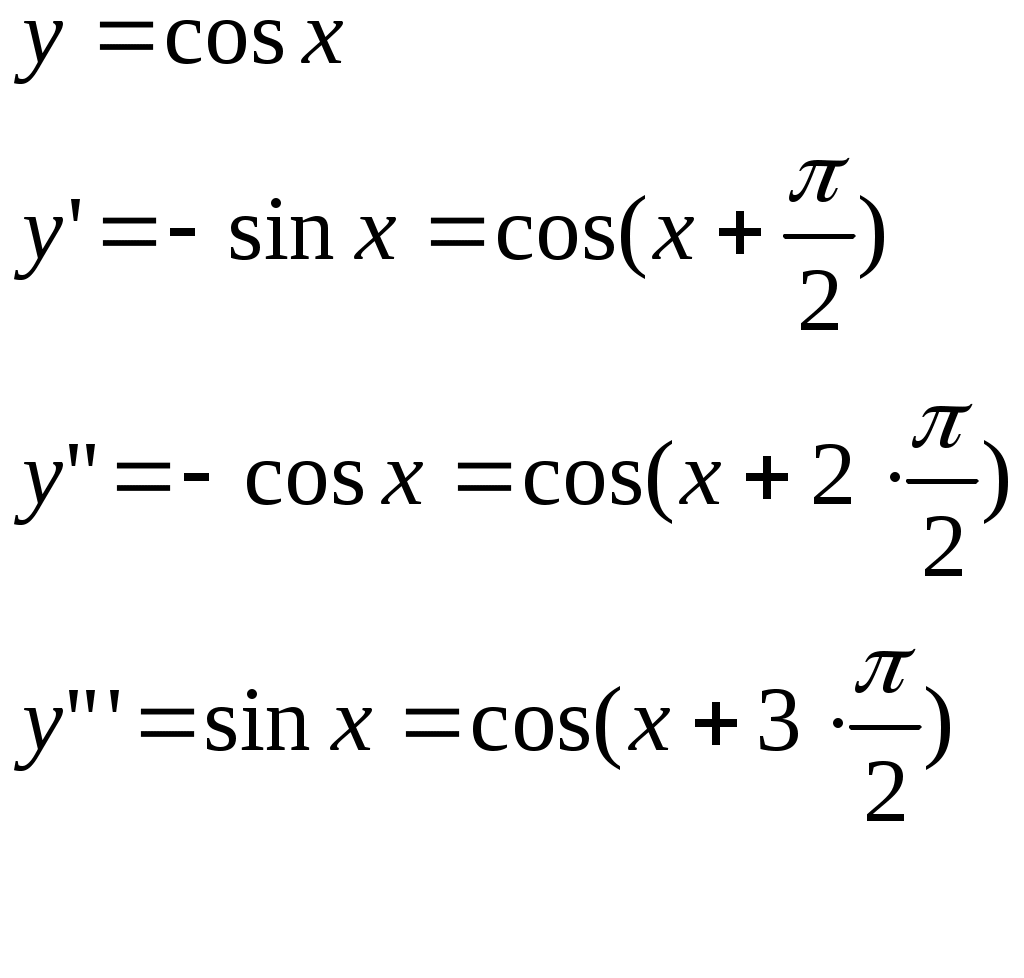 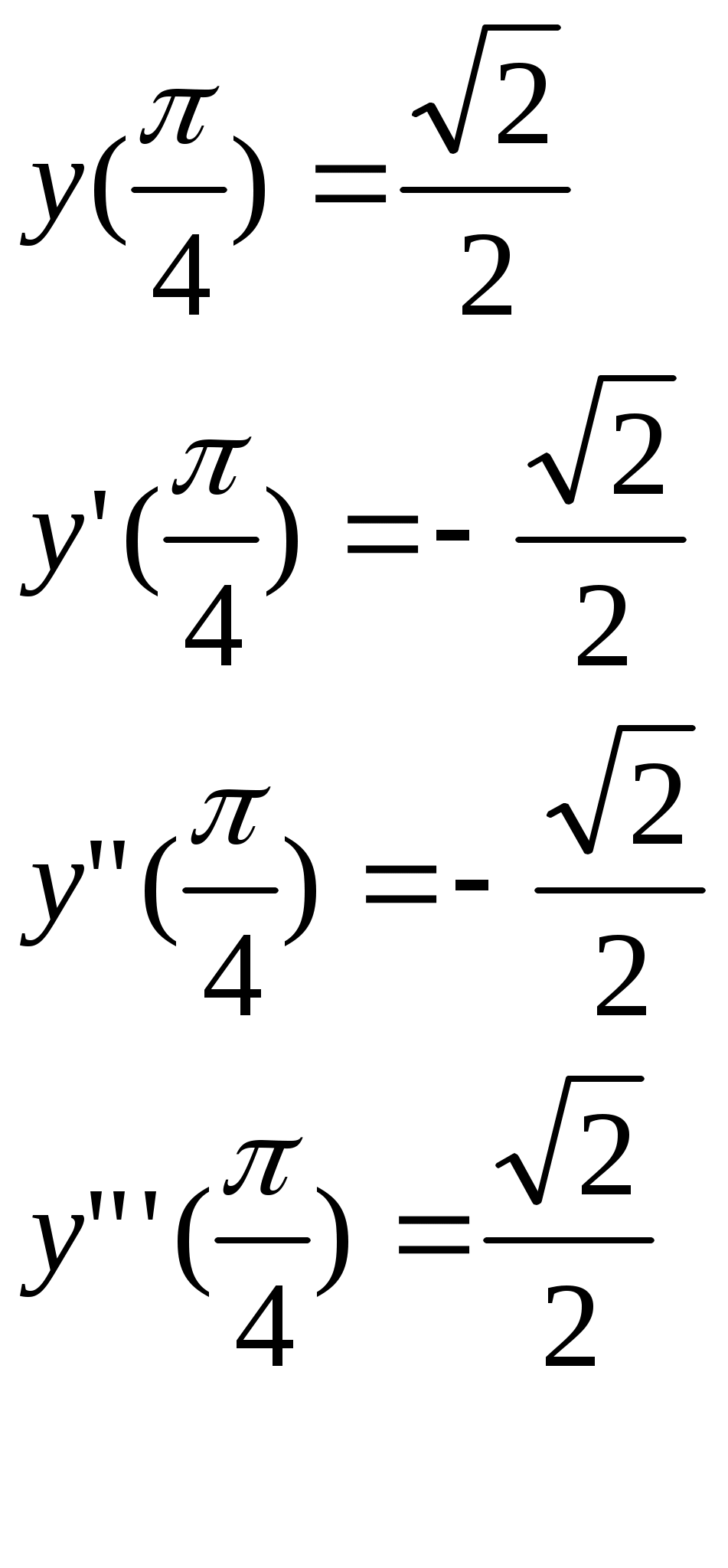 ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ ___ 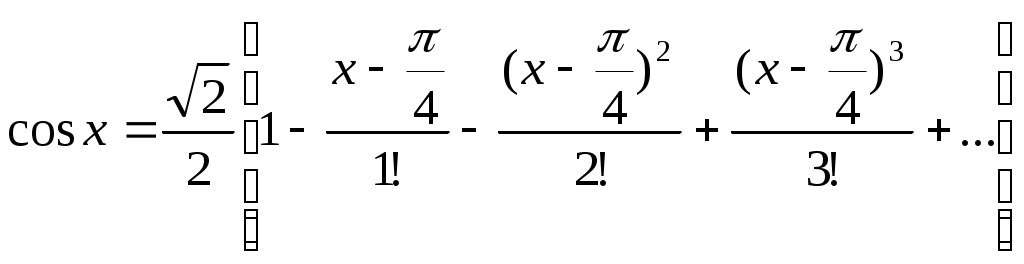 Исследуем соответствующий остаточный член 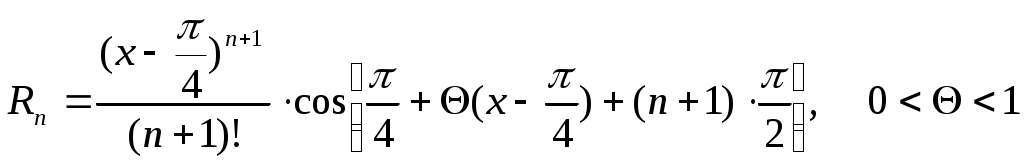 Каково бы ни было значение 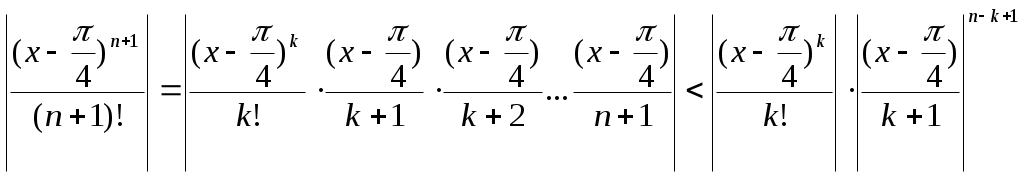 Первый множитель 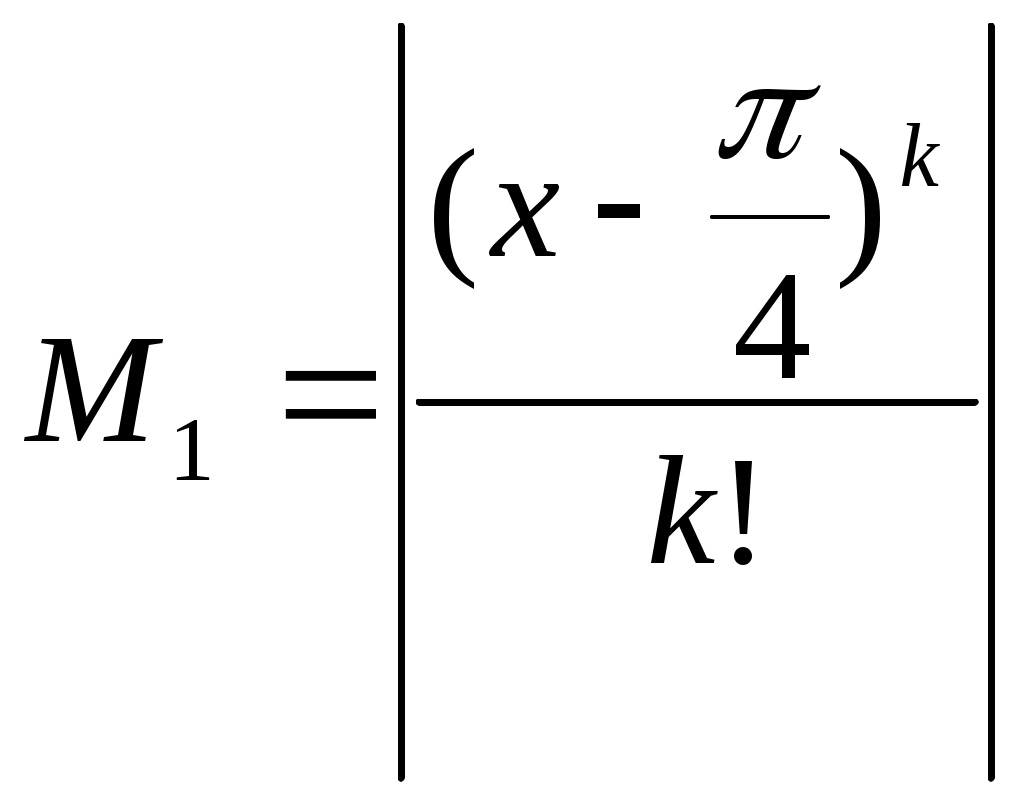 не зависит от не зависит от 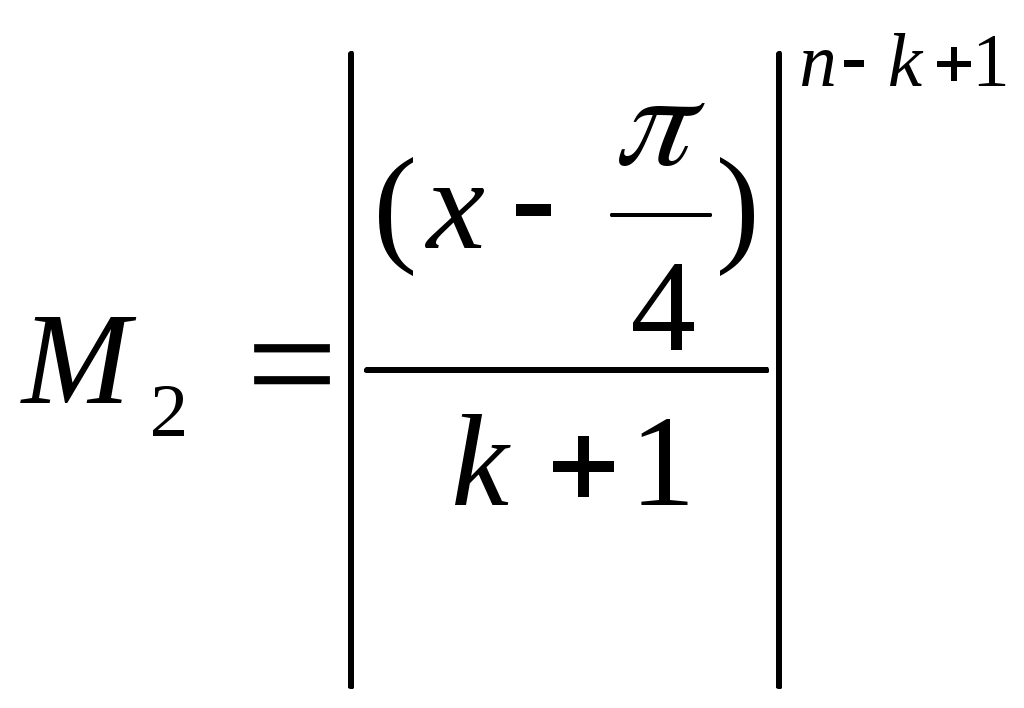 при при 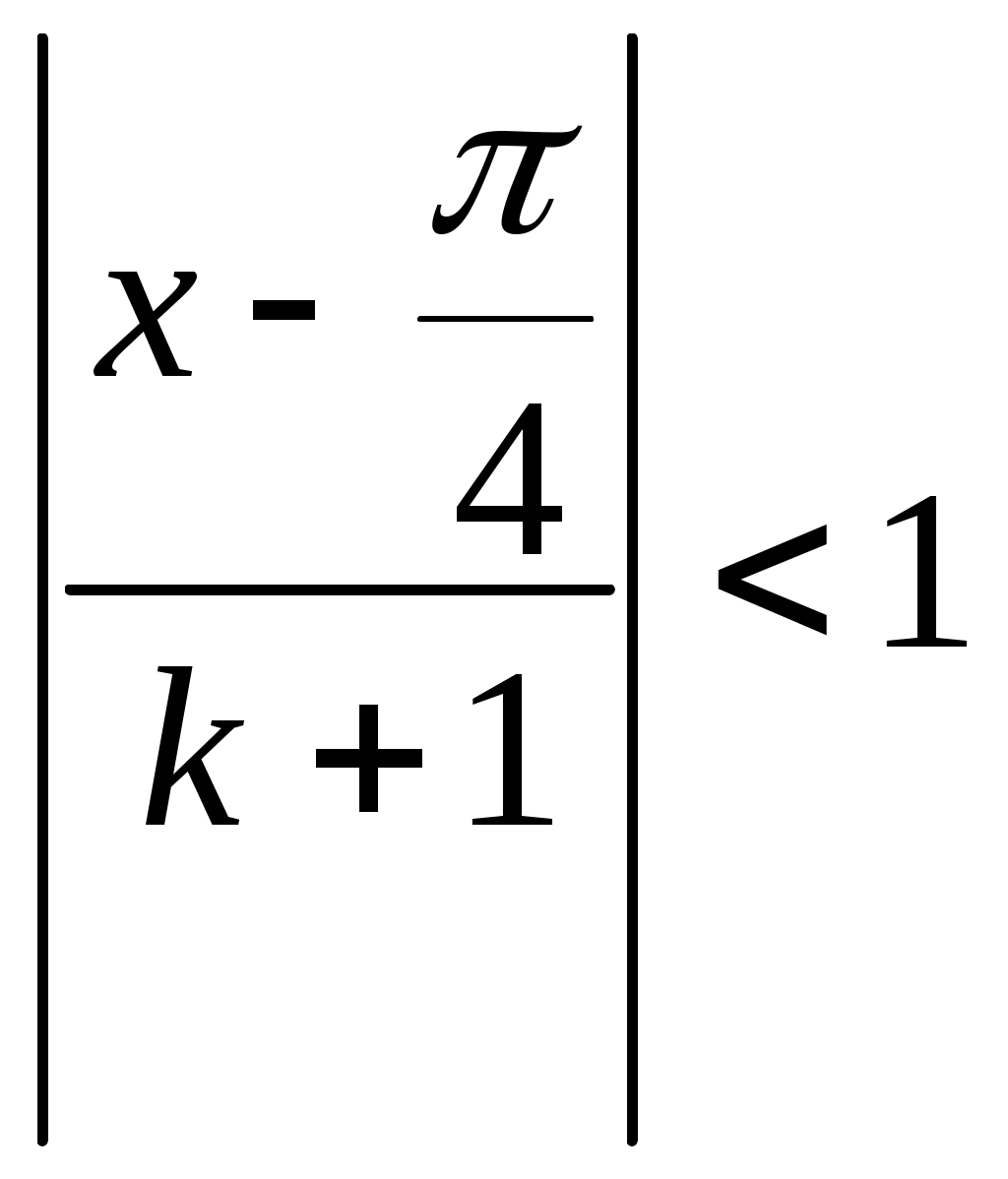 . Следовательно, . Следовательно, 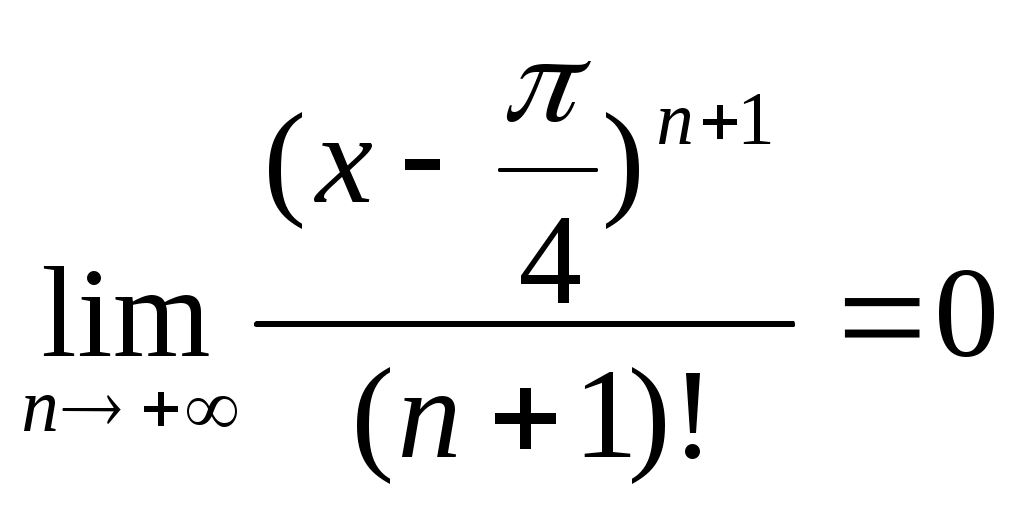 , а , а Поэтому Определение. Если в ряде Тейлора положить x0=0, получим частный случай ряда Тейлора, который называется рядом Маклорена. Он имеет вид: Остаточный член ряда Маклорена в форме Лагранжа имеет вид: Чтобы он стремился к нулю, достаточно ограниченности производной Разложения стандартных функций в ряды Маклорена имеют вид: 1) 2) 3) 4) биномиальный ряд: (сходится при -1 5) 6) Пример. Разложить в ряды Маклорена функции: 1) Решение: 1) Т.к. ряд Маклорена ex сходится на всей числовой оси, то и полученный ряд сходится к данной функции, при всех значениях x. 2) Преобразуем функцию к виду 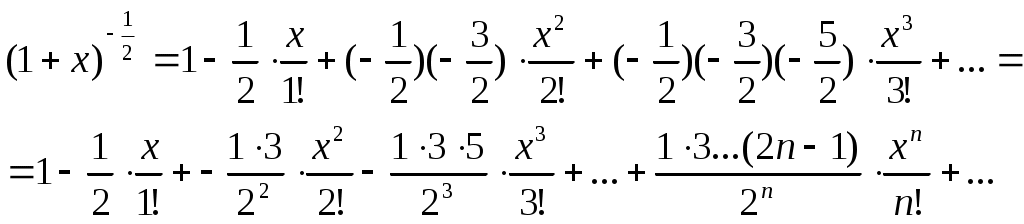 Заменяя в этом выражении x на 3x, получаем: Окончательно. Биномиальный ряд сходится при -1 3) Преобразуем данную функцию: (второй ряд получен из первого путем замены x на 2x) и складывая их почленно, имеем: Задачи для решения: 171) Разложить функцию 172) Разложить функцию 173) Разложить функцию 174) Разложить функцию 175) Разложить функцию 176) Разложить функцию 177) Разложить функцию 178) Разложить функцию 179) Разложить функцию В задачах 180- 186 найти первые пять членов ряда Тейлора для данной функции в окрестности точки x0: 180) 181) 182) 183) 184) 185) 186) В задачах 187-201 разложит данные функции в окрестности точки x=0, пользуясь формулами разложения в ряд Маклорена функций ex, sinx, cosx, ln(1+x), (1+x)mи arctgx: 187) 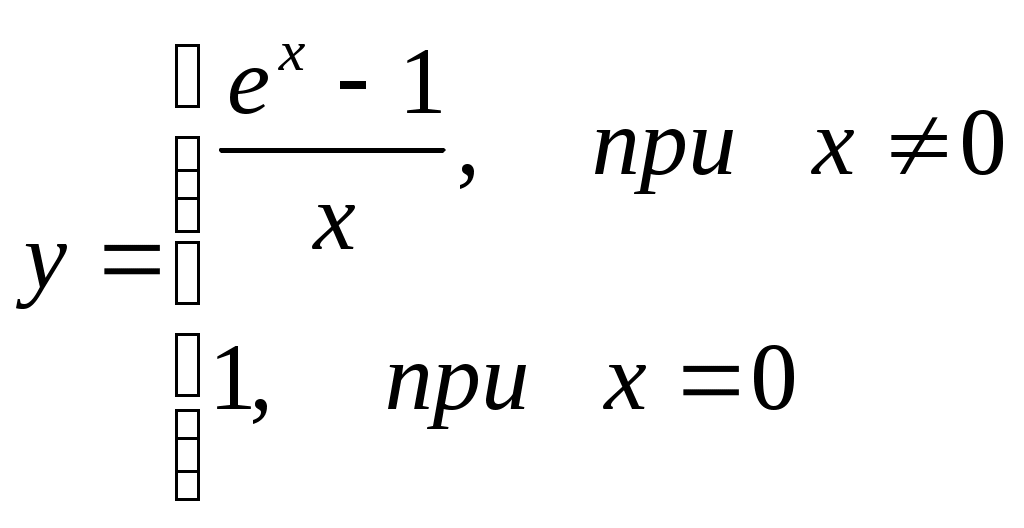 187) 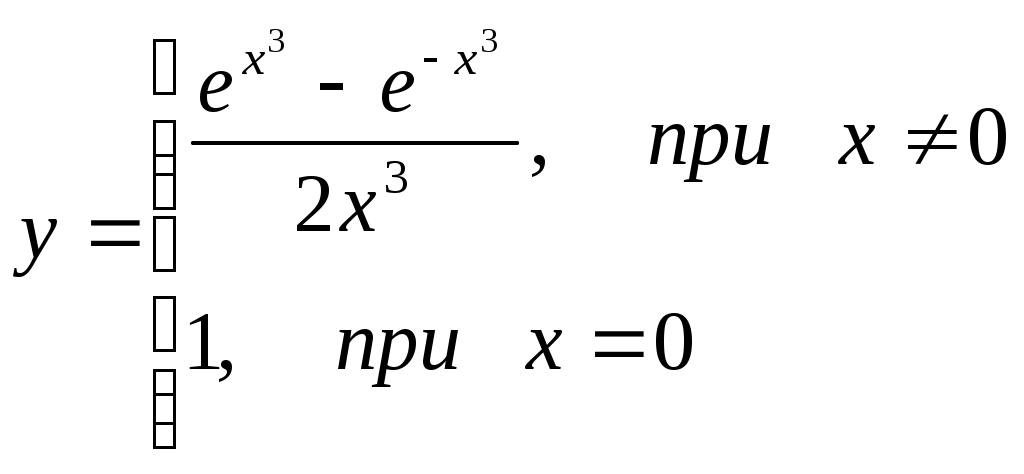 188) 189) 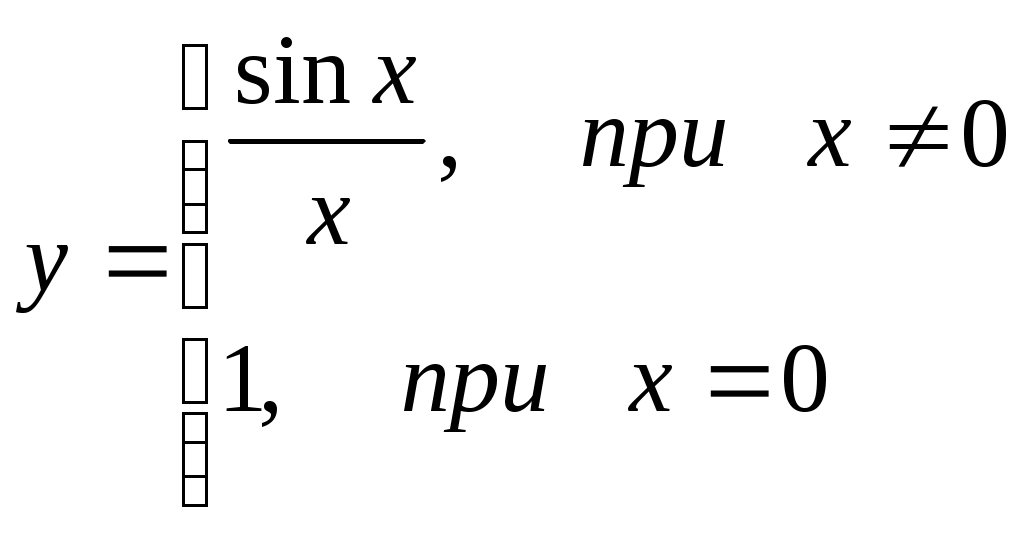 190) 191) 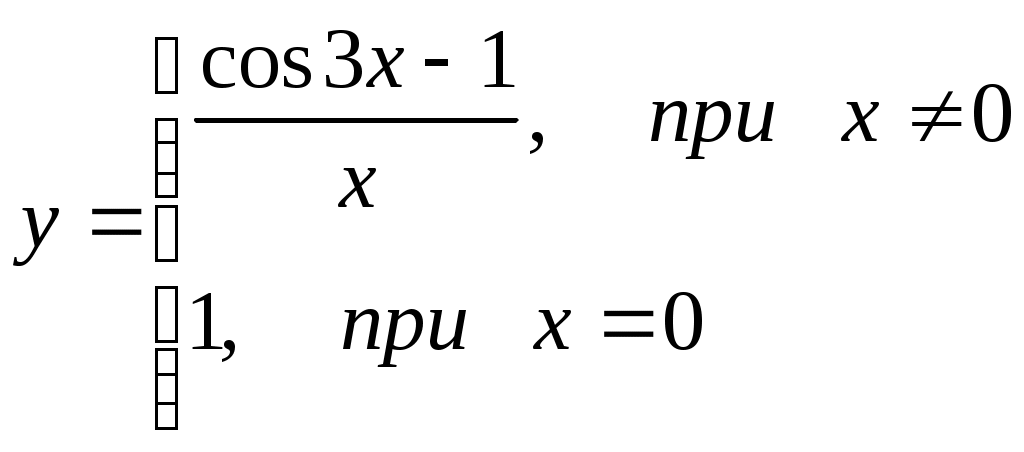 192) 193) 194) 195) 196) 197) 198) 199) 200) 201) 202) Пользуясь разложением функции в ряд Тейлора, найти значение: 1) седьмой производной функции 2) пятой производной функции 3) десятой производной функции |
