ряды фурье. Ряды.Ряды Фурье.Сборник задач. Сборник задач по высшей математике. РостовнаДону 2008г. 1

• Название: Сборник задач по высшей математике. РостовнаДону 2008г. 1
• Анкор: ряды фурье
• Дата: 03.05.2023
• Размер: 1.93 Mb.
• Имя файла: Ряды.Ряды Фурье.Сборник задач.doc
• Тип: Сборник задач; #1106375
• страница: 4 из 5

§5. Применение рядов к приближенным вычислениям.
5.1 Приближенное вычисление значений функции.
Допустим, что в окрестности некоторой точке x₀ функция f(x) разлагается в ряд Тейлора. Тогда точное значение функции f(x) в любой точке этой окрестности может быть вычислено по ряду Тейлора, а приближенное ее значение – по частичной сумме этого ряда. Возникающую при этом ошибку можно оценивать по остаточному члену ряда: в случае знакочередующегося ряда – при помощи теоремы Лейбница (ошибка не превосходит по модулю первого отброшенного члени); в случае знакоположительного ряда стараются подобрать другой ряд (обычно геометрическую прогрессию), члены которой больше членов остатка и сумму которой мы можем найти.

Пример. Пользуясь разложением в ряд Маклорена вычислить с точностью до 0,0001 значение .

Решение:

Преобразуем данный корень и применяем биноминальный ряд, пологая , :

.

Чтобы определить, сколько взять первых членов этого знакочередующегося ряда для вычисления с точностью до 0,0001, вычисляем несколько последовательных первых членов ряда: a₁=1; a₂≈0,1562; a₃≈0,00037; a₄≈0,00001.

Согласно теореме Лейбница, если ограничиться суммой первых трех членов ряда, то ошибка искомого приближенного значения будет меньше 2a₄≈2∙0,00001<0,0001.

Следовательно ≈2(1+0,01562-0,00037)≈2,0305.
5.2 Вычисление пределов.
Пример. Вычислить предел, пользуясь разложением функций в ряд Маклорена:



Решение:

Разложим функции в ряды Маклорена: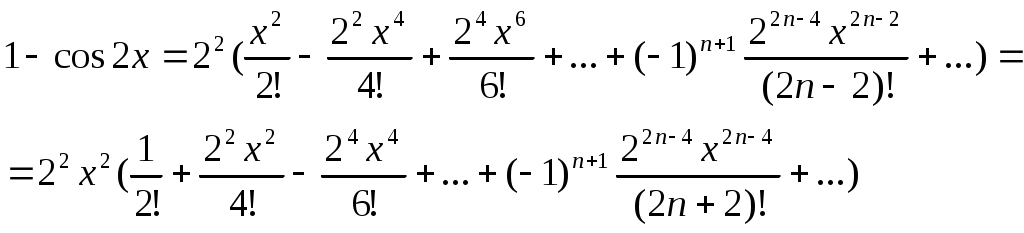

;

;

;

;

Подставим полученные ряды в выражение, стоящее под знаком предела:

.
5.3. Вычисление интегралов.
Неопределенные интегралы, не имеющие выражения в конечном виде через элементарные функции, могут быть представлены в виде рядов.

Пример. Разлагая подынтегральную функцию в ряд Маклорена и интегрируя его почленно, найти разложение в ряд интеграла:

.

Решение:

Пользуясь рядом Маклорена для sinx, заменяя в нем x на x², имеем:



Полученный ряд является сходящимся при любых значениях x, следовательно, можно интегрировать при любом x.

.

Определенные интегралы, которые, как функции верхнего предела, не выражаются через элементарные функции, так же бывает удобно вычислять с помощью рядов. При этом подынтегральную функцию разлагают в ряд Тейлора, и если пределы интеграла лежат внутри интервала сходимости, то ряд можно проинтегрировать почленно.

Пример. С помощью рядов вычислить с точностью до 0,0001 приближенное значение интеграла:

.

Решение:

Пользуясь рядом Маклорена для arctgx, получим:



Деля обе части равенства на x и интегрируя, найдем: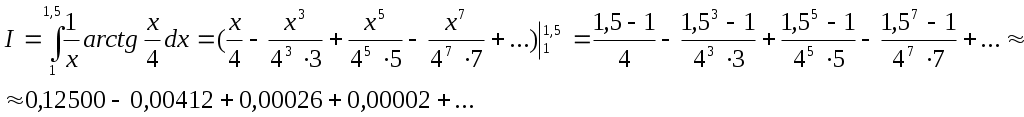



Полученный ряд представляет собой сходящийся ряд, четвертый член которого меньше 0,0001. Поэтому для вычисления искомого приближенного значения достаточно взять сумму трех первых членов ряда. В результате получим приближенное значение с заданной точностью:

I≈0,1211.
5.4 Интегрирование дифференциальных уравнений с помощью рядов.
Пусть задано дифференциальное уравнение и начальные условия, определяющие частное решение. Допустим, что решение уравнения в окрестности x₀, в которой заданы начальные условия, можно разложить в степенной ряд по степеням x-x₀:

y=a₀+a₁(x-x₀)+a₂(x-x₀)²+...

Продифференцируем этот ряд пока с неопределенными коэффициентами столько раз, каков порядок уравнения. Подставляя затем в уравнение вместо функции и ее производных соответствующие ряды, мы получим тождество, из которого и определяем неизвестные коэффициенты ряда. При этом первые коэффициенты ряда определяются из начальных условий.

Такой метод решения называется методом неопределенных коэффициентов.

Пример: Найти четыре первых члена разложения в степенной ряд частного решения уравнения , удовлетворяющего начальному условию y(0)=1

Решение:

Ищем решение в виде степенного ряда:

y=a₀+a₁x+a₂x²+...+a_nxⁿ+...

Согласно начальному условию y(0)=a₀=1.

Далее найдем ряды для и :

=a₁+2a₂x+3a₃x²+...+(n+1)a_n+1xⁿ+...

=a₀²+2a₀²x+(a₁²+2a₀²x)x²...

Подставим их в ряд для cosx в исходное уравнение:

a₁+2a₂x+3a₃x²+...+x(a₀²+2a₀²x+(a₁²+2a₀²x)x²+...)=2-x²...

Отсюда путем сравнения коэффициентов при одинаковых степенях x из обеих частей равенства найдем:

; ; .

Следовательно, искомое частное решение есть:



Если подстановка рядов вместо y и ее производных приводит к сложным уравнениям для определения, может быть применен метод последовательного дифференцирования.

Пример. Найти разложение в степенной ряд частного решения уравнения , удовлетворяющего начальным условиям: y(0)=1; y’(0)=0.

Решение:

Пусть искомая функция y(x) разложена в ряд Маклорена

,

где величины ,..., являются значениями функции y(x) и ее производных при x=0,

а следующие коэффициенты найдем путем последовательного дифференцирования данного уравнения:

; ;

; ; ;

; ;

... ...

.

Подставляя эти значения коэффициентов в ряд Маклорена получим искомое частное решение в виде ряда:

,

который сходится при любом значении x.
Задачи для решения.
В задачах 203-216, пользуясь формулами разложения в ряд Маклорена функций e^x, sinx, cosx, ln(1+x), (1+x)^m, arctgx, вычислить с заданной точностью:

203) с точностью до 0,0001.

204) с точностью до 0,0001.

205) с точностью до 0,0001.

206) с точностью до 0,0001.

207) с точностью до 0,0001.

208) с точностью до 0,0001.

209) с точностью до 0,0001.

210) с точностью до 0,0001.

211) с точностью до 0,0001.

212) с точностью до 0,0001.

213) с точностью до 0,0001.

214) с точностью до 0,0001.

215) с точностью до 0,0001.

216) с точностью до 0,0001.

В задачах 217-228 пользуясь разложением функций в ряд Маклорена, вычислить пределы:

217) ;

218) ;

219) ;

220) ;

221) ;

222) ;

223) ;

224) ;

225) ;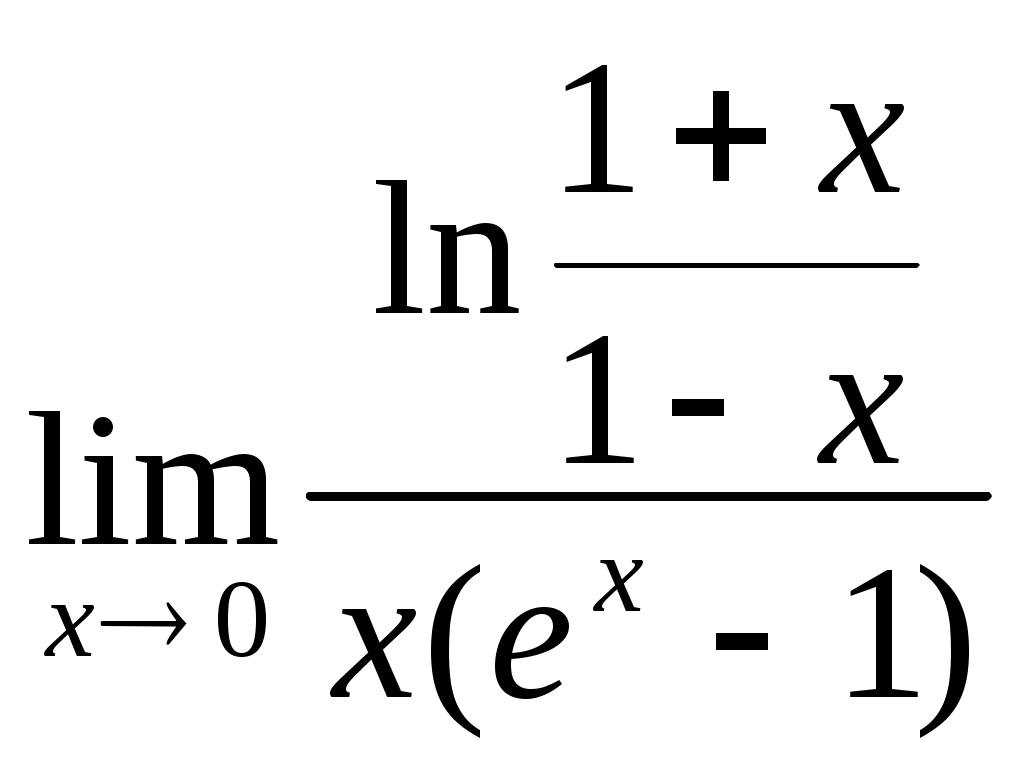

226) ;

227) ;

228) ;

В задачах 229-237 выразить в форме ряда интегралы, используя разложение в ряд подынтегральных функций; указать области сходимости полученных рядов.

229) ;

230) ;

231) ;

232) ;

233) ;

234) ;

235) ;

236) ;

237) .

В задачах 238-241 вычислить приближенные значения определенных интегралов, взяв указанное число членов разложения подынтегральной функции в ряд; указать погрешность:

238) (3 чл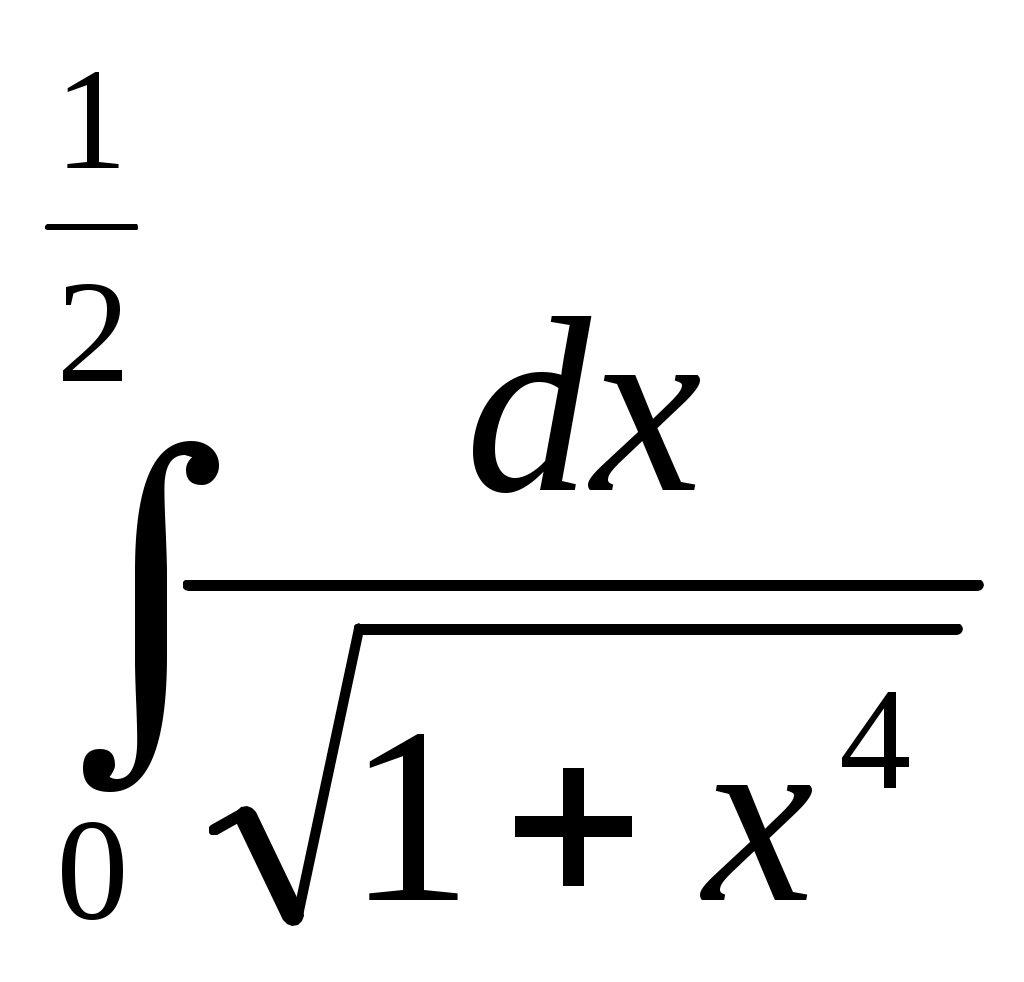ена);

239) (2 члена);

240) 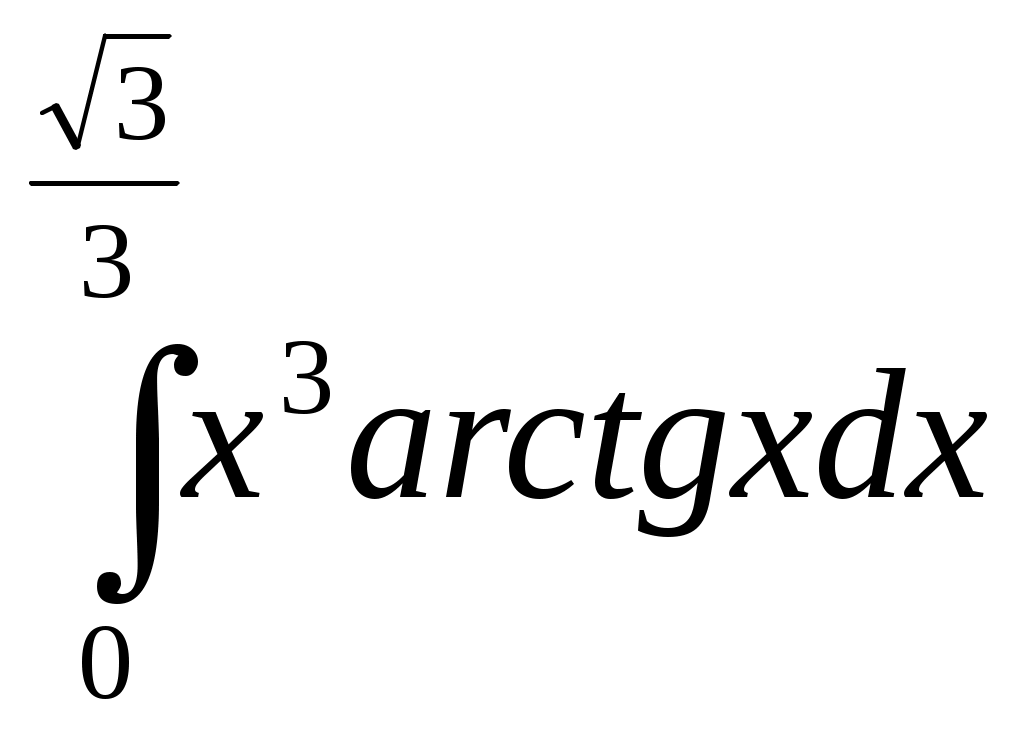(3 члена);

241) (6 членов);

В задачах 242-259 вычислить с точностью до 0,001=δ интегралы:

242) ;

243) ;

244) ;

245) ;

246) ;

247) ;

248) ;

249) ;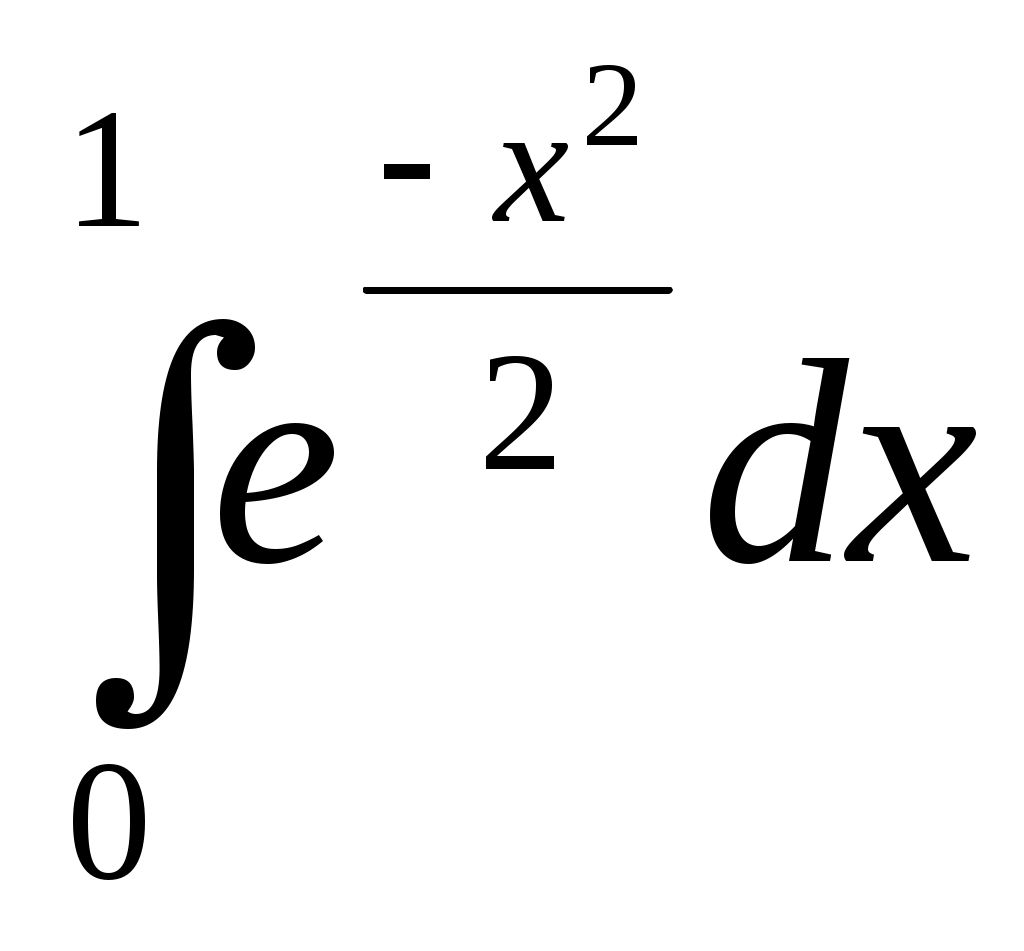

250) ;

251) ;

252) , δ=10^-4;

253) ;

254) ;

355) , δ=10^-2;

356) , δ=10^-4;

357) , δ=10^-4;

358) , δ=10^-4;

359) , δ=10^-4.

В задачах 260-279 найти пять первых членов разложения в степенной ряд частного решения дифференциального уравнения при заданных начальных условиях:

260) ; y(0)=1.

261) ; y(0)=1.

262) ; y(0)=1.

263) ; y(0)=1.

264) ; y(0)=0.

265) ; y(0)=2.

266) ; y(0)=1.

267) ; y(0)=1.

268) ; y(0)=1.

269) ; y(0)=1.

270) ; y(0)=1, y’(0)=2.

271) ; y(0)=4, y’(0)=2.

272) ; y(0)=1, y’(0)=1.

273) ; y(0)=1, y’(0)=1.

274) ; y(0)=а, y’(0)=0.

275) ; y(0)=0, y’(0)=1.

276) ; y(0)=2, y’(0)=2.

277) ; y(0)=0, y’(0)=1.

278) ; y(0)=1, y’(0)=0.

279) ; y(0)=1, y’(0)=1.

В задачах 280-287 методом неопределенных коэффициентов найти пять первых членов разложения в степенной ряд частного решения дифференциального уравнения:

280) ; y(0)=0, y’(0)=1.

281) ; y(0)=0, y’(0)=1.

282) ; y(0)=0, y’(0)=1.

283) ; y(0)=1, y’(0)=0.

284) ; y(0)=0, y’(0)=1.

285) ; y(0)=1.

286) ; y(0)=-2.