ДУ Ряды. Решение уравнение с разделяющими переменными Ответ б Решение уравнение Бернулли
 Скачать 35.29 Kb. Скачать 35.29 Kb.
|
|
Задание 1. Решить дифференциальные уравнения: а) 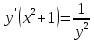 Решение: уравнение с разделяющими переменными 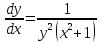 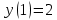 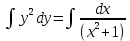 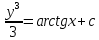 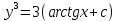 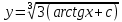 Ответ: 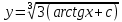 б) 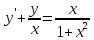 Решение: уравнение Бернулли 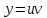 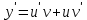 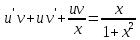 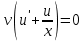 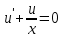 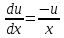 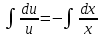 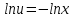 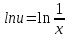 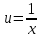 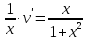 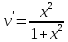 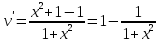 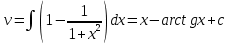 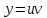 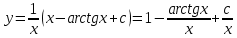 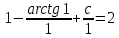 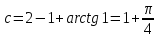 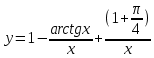 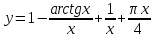 Ответ: 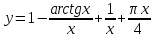 в) 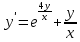 Решение: однородное уравнение 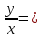 u u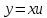 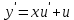 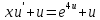 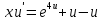 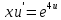 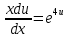 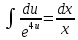 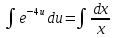 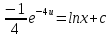 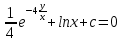 Ответ: 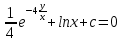 г) 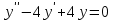 Решение: однородное дифференциальное уравнение 2 порядка 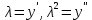 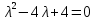 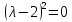 𝝀=2 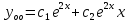 Ответ: 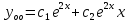 д) 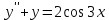 Решение: неоднородное дифференциальное уравнение 2 порядка 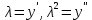 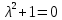 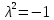 𝝀=i 𝝀=-i 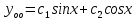 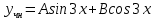 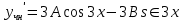 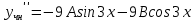 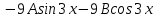 + +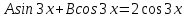 (-9A+A)sin3x-(9B-B)cos3x=2cos3x (-9A+A)sin3x-(9B-B)cos3x=2cos3x -8Asin3x-8Bcos3x=2cos3x sin3x: -8A=0, A=0 cos3x: 9B-B=2 8B=2, B= 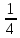 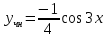 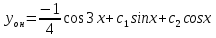 Ответ: 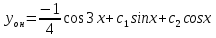 Задание 2. Исследовать на сходимость числовые ряды: a) 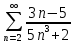 Используем предельный признак сравнения: Рассмотрим сходящийся ряд 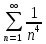 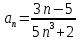 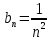 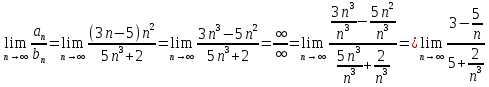 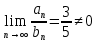 Значит, исследуемый ряд 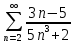 сходится вместе с рядом сходится вместе с рядом 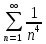 a) 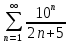 Используем признак сравнения Даламбера: 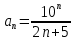 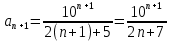 D= 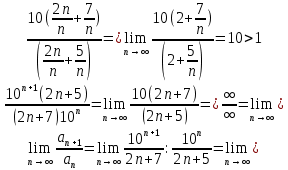 Данный ряд расходится. Задание 3. Исследовать ряд на абсолютную и условную сходимость 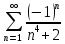 Данный ряд является знакочередующимся числовым рядом 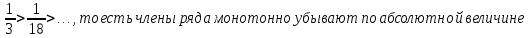 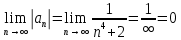 Ряд сходится по признаку Лейбница. Исследуем ряд на абсолютную сходимость: 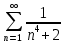 Сравним данный ряд со сходящимся рядом 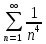 Используем предельный признак сравнения: 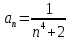 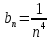 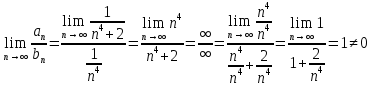 Значит, исследуемый ряд 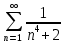 сходится с рядом сходится с рядом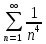 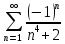 сходится абсолютно. сходится абсолютно.Задание 4. Найти интервал сходимости степенного ряда и исследовать сходимость ряда на концах интервала сходимости: а) 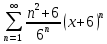 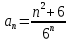 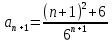 R= 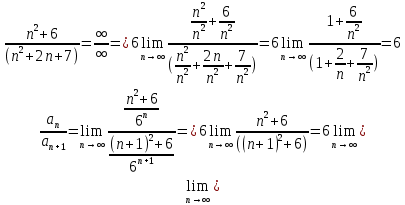 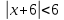 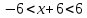 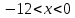 Исходный ряд является абсолютно сходящимся при всех 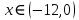 Проверим сходимость ряда на концах интервала сходимости: х=-12 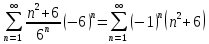 - числовой знакочередующийся ряд, исследуем его по признаку Лейбница. - числовой знакочередующийся ряд, исследуем его по признаку Лейбница.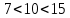 , , 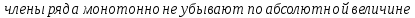 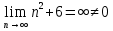 Оба условия Лейбница не выполняются, значит ряд 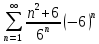 расходится. расходится.х=0 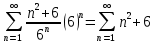 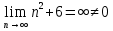 Ряд 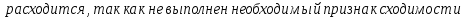 Исходный ряд 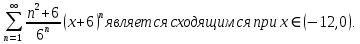 б) 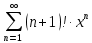 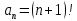 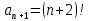 R= 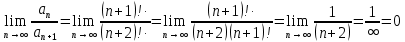 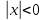 х=0 Исходный ряд является абсолютно сходящимся при х=0 |
