ряды фурье. Ряды.Ряды Фурье.Сборник задач. Сборник задач по высшей математике. РостовнаДону 2008г. 1
 Скачать 1.93 Mb.
|
|
§3. Функциональные ряды. Область сходимости функциональности ряда. 3.1 Основные определения. Определение. Ряд  называется функциональным, если его члены являются функциями переменной  : При различных значениях из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.Определение. Совокупность значений , при которых функциональный ряд сходится, называется областью его сходимости.В области сходимости ряда его сумма является некоторой функцией от , поэтому сумму функционального ряда обозначают  .Пример. Функциональный ряд  сходится при всех  , т.е. в интервале (-1;1), т.к. при любом из этого интервала соответствующий числовой ряд представляет собой бесконечно убывающую геометрическую прогрессию.В интервале сходимости сумма ряда  При всех  этот ряд расходится.Обозначим  сумму первых  членов ряда. Если ряд сходится и сумма его , то  ,где   называется остатком ряда. Для всех в области сходимости ,Поэтому  ,Т.е. остаток сходящегося ряда стремится к нулю.3.2 Степенные ряды. Из всех функциональных рядов простейшими и наиболее употребительными являются степенные ряды вида.  Или более общего вида  Где  - постоянные числа, называемые коэффициентами ряда.Ряд (2) подстановкой  преобразуется в ряд вида (1), поэтому в дальнейшем будем заниматься рядами вида (1).Теорема Абеля. Если степенной ряд (1) сходится при некотором значении  , не равном нулю, то он абсолютно сходится при всяком значении , для которого  ;Если ряд расходится при некотором значении  , то он расходится при всяком , для которого  Из теоремы Абеля следует, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число  , что для всех , по модулю меньших  ряд абсолютно сходится, а для всех , по модулю больших  , ряд расходится.Определение. Радиусом сходимости степенного ряда (1) называется такое число , что для всех ,  , степенной ряд сходится, а для всех  , расходится. Интервал  называется интервалом сходимости.3.3. Определение интервалов сходимости степенных и функциональных рядов. Пусть имеем ряд  Рассмотрим ряд, составленный из абсолютных величин его членов.  Для определения сходимости этого ряда с положительными членами применим признак Даламбера. Допустим, что существует предел: 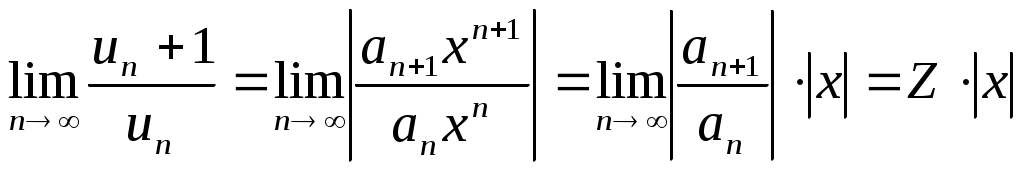 По признаку Даламбера ряд (2) сходится, если  , т.е. если  , и расходится, если  . Следовательно, ряд (1) сходится абсолютно, при , а если , то  и ряд (2) расходится, причем его общий член не стремится к нулю ( не выполняется необходимый признак сходимости), а значит, ряд (1) расходится.Интервалом сходимости ряда (1) является интервал  , а радиус сходимости  При исследовании вопроса о сходимости ряда на концах интервала сходимости признак Даламбера не применим т.к. соответствующий предел здесь равен единице, поэтому здесь надо применить какой-либо другой признак. Пример. Определить интервал сходимости степенного ряда:  Составляем ряд из модулей:  Как следует из ряда,  ,  Далее, используя признак Даламбера, ищем предел  И определяем, при каких значениях этот предел будет меньше единицы, т.е. решаем неравенство   Согласно признаку Даламбера, при любом значении из найденного интервала данный ряд сходится (абсолютно), а при  расходится.Граничные точки  этого интервала, для которых  и признак Даламбера не решает вопроса о сходимости ряда, исследуем особо.При  получим числовой ряд с положительными членами  , который расходится, что следует из сравнения его с расходящимся гармоническим рядом  При  получим числовой знакочередующийся ряд  , который сходится согласно признаку Лейбница. Члены ряда убывают по абсолютному значению, стремясь к нулю. Следовательно, интервалом сходимости данного степенного ряда является полуоткрытый интервал  3.4 Свойства степенного ряда. 1. Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда. 2. Если степенной ряд  имеет интервал сходимости (  ), то ряд ,полученный почленным дифференцированием ряда (1), имеет тот же интервал сходимости ( ), при этом  ,если , т.е внутри интервала сходимости производная от суммы степенного ряда (1) равна сумме ряда, полученного почленным дифференцированием ряда (1).3. Степенной ряд можно почленно интегрировать в интервале сходимости  Задачи для решения. В задачах 129-150 найти область сходимости степенных рядов: 129)  130)  131)  132)  133)  134)  135)  136)  137)  138)  139)  140)  141)  142)   143)  144)  145)  146)  147)  148)  149)  150)  В задачах 151-166 найти область сходимости заданных функциональных рядов: 151)  152)  153)  154)  155)  156)  157)  158)  159)  160)  161)  162)  163)  164)  165)  166)  Используя интегрирование и дифференцирование степенных рядов, найти сумму заданных рядов: 167)  168)  169)  170)  |