ЧАСТЬ 1
|
1. Единицы физических величин и погрешности их измерений
|
1.1.Б. Единицы физических величин (базовые вопросы)
|
|
Укажите группу основных единиц физических величин в СИ (Системе Интернациональной).
|
1. кг, А, м, с, м/с, кд, моль.
2. С, кг, м, кд, А, моль, с.
3. Н, кг, м, кд, А, моль, К.
4. К, с, кг, м, кд, А, моль.!
|
|
Какая из перечисленных физических величин имеет размерность 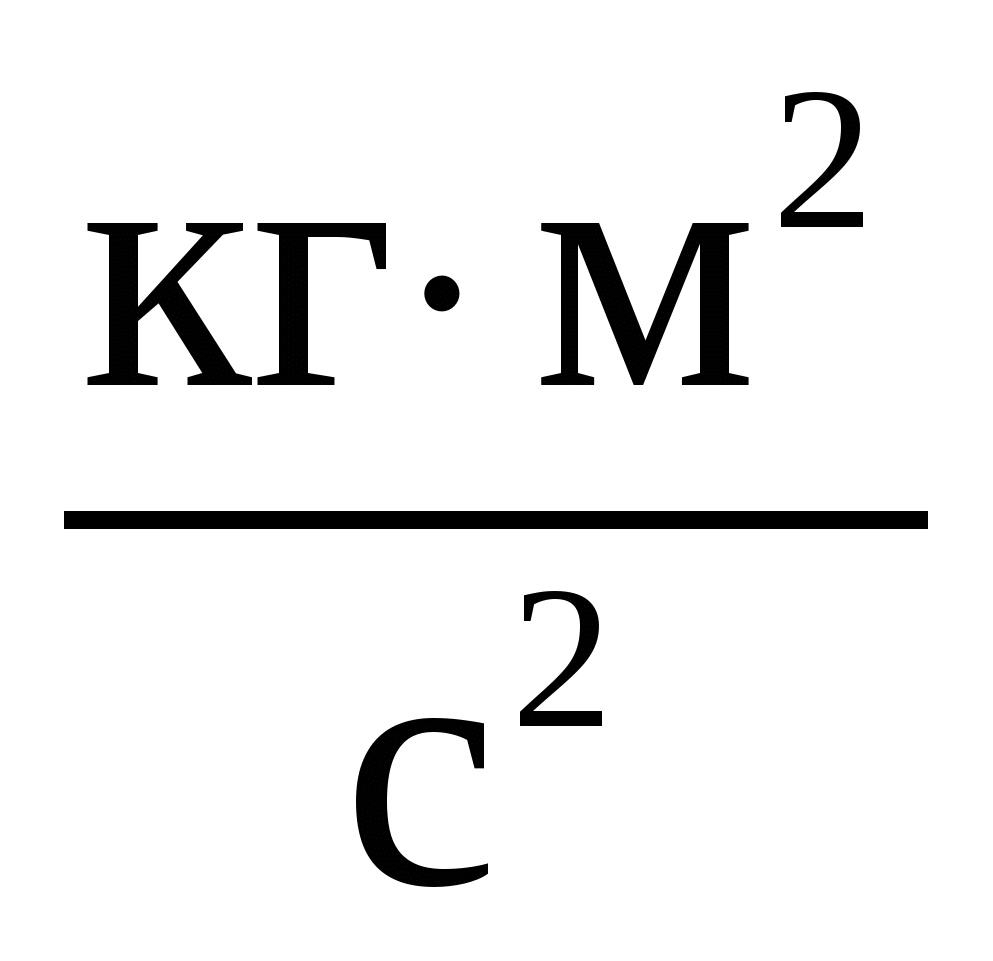 ? ?
|
1. Момент силы.!
2. Импульс.
3. Момент импульса.
4. Сила.
|
|
Какая из представленных физических величин имеет единицу измерения, совпадающую с единицей измерения силы?
|
1. Мощность.
2. Давление.
3. Вес.!
4. Импульс.
|
|
Единицей измерения энтропии в системе СИ является…
|
1. Н∙ К /м.
2. Дж/К.!
3. Дж/м.
4. Н∙м/К.
|
|
Какая из перечисленных физических величин имеет размерность 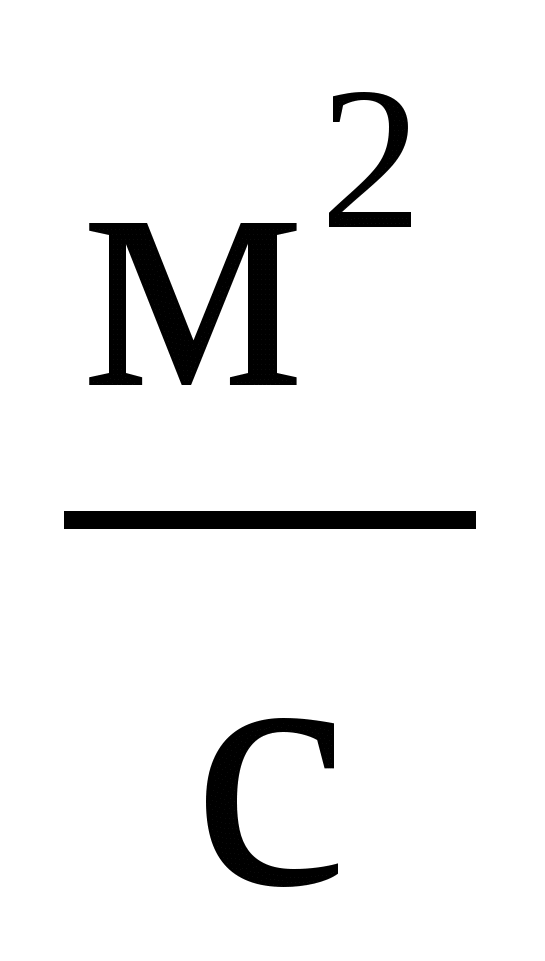 ? ?
|
1. Скорость.
2. Импульс.
3. Динамическая вязкость.
4. Кинематическая вязкость.!
|
|
Размерность момента силы…
|
1. 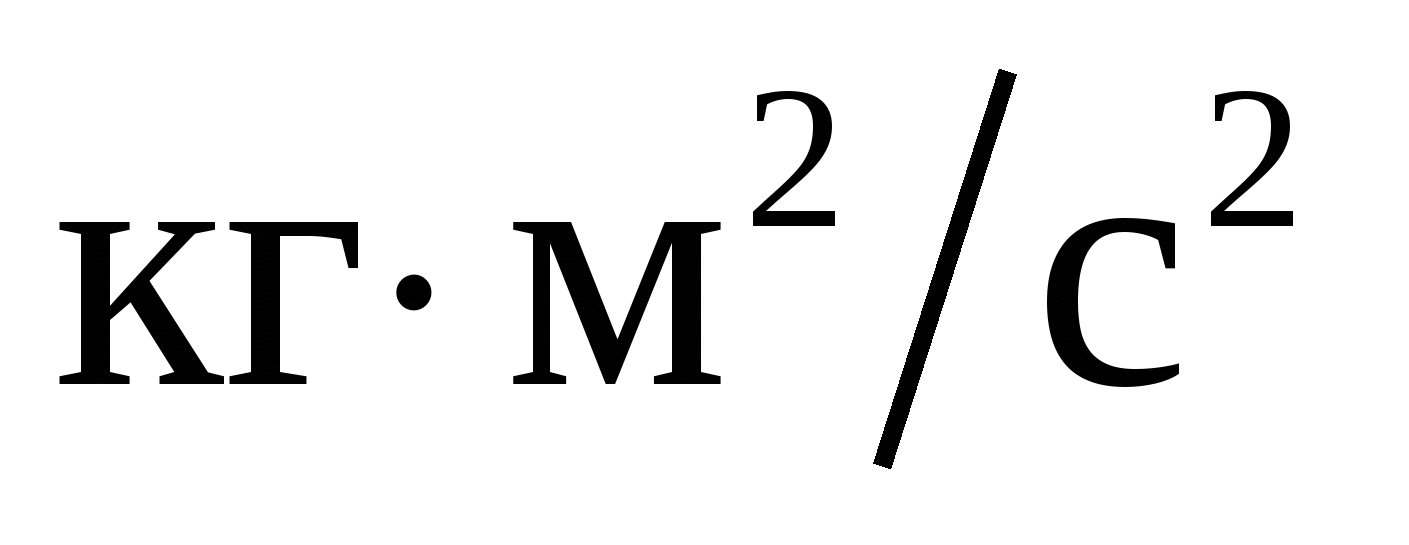 .! .!
2. 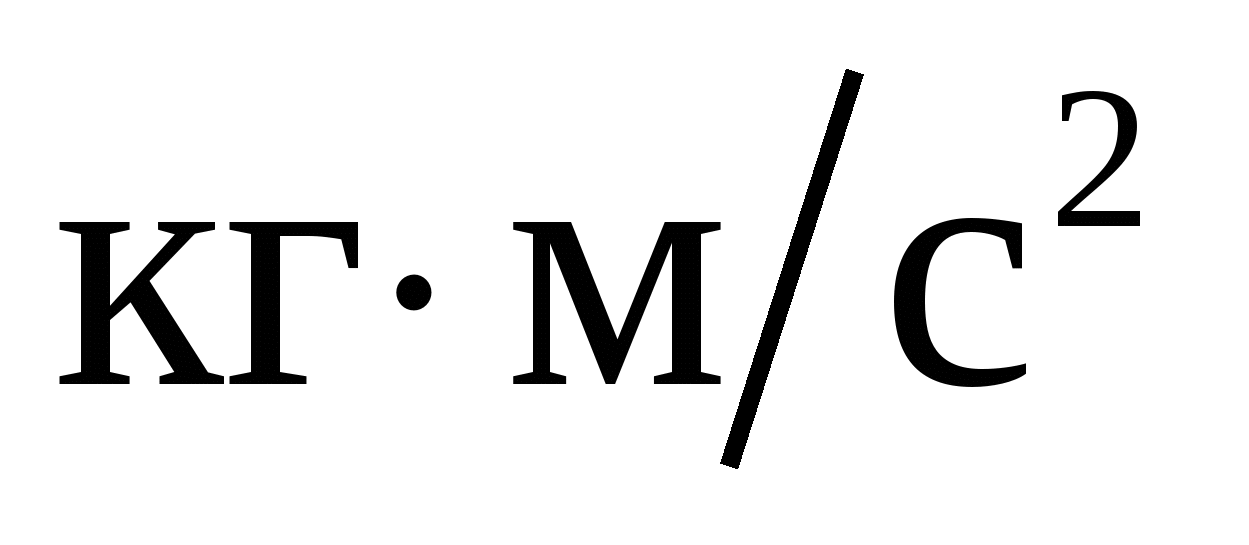 . .
3. 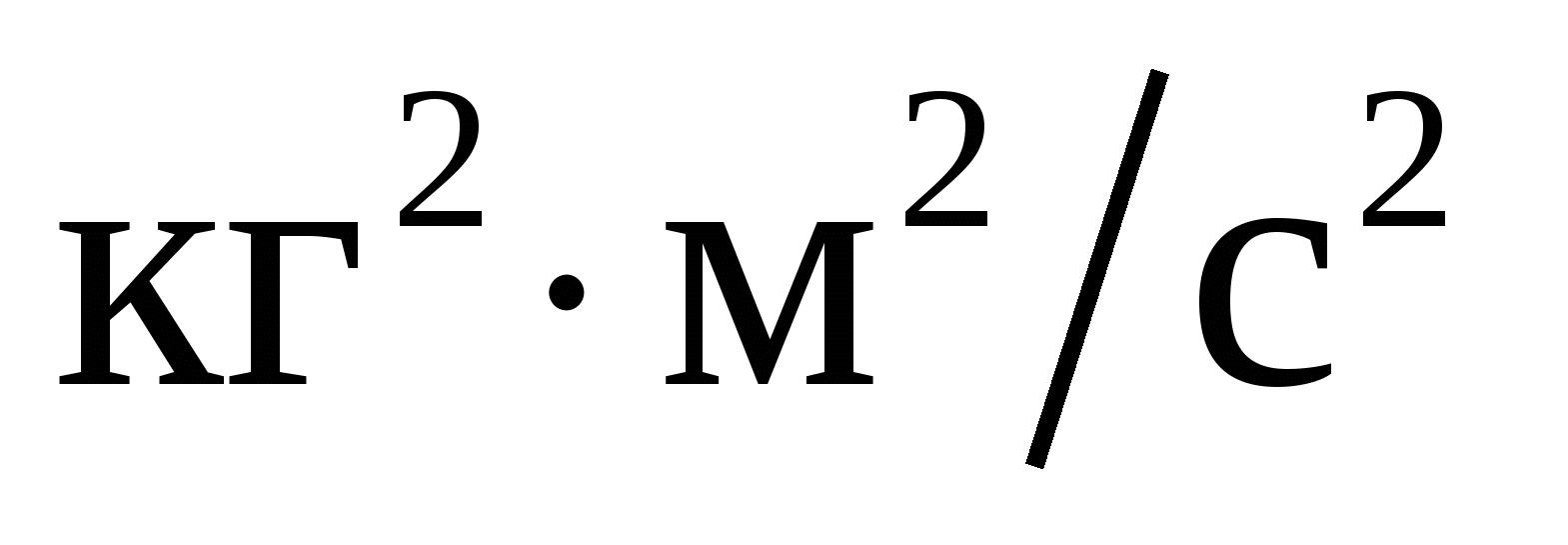 . .
4. 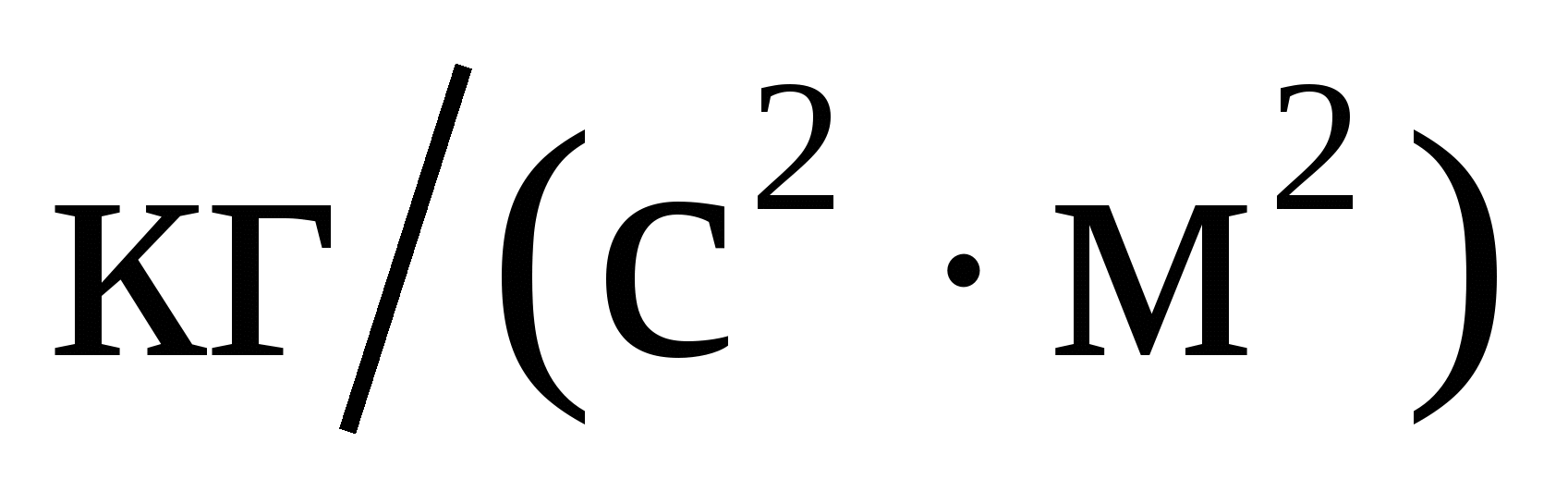 . .
|
|
Единицей измерения мощности в системе СИ является…
|
1. Па∙с.
2. Н/с.
3. Дж/с.!
4. Вт/с.
|
|
Размерность коэффициента динамической вязкости?
|
1. кг/(м с2).
2. м с2.
3. кг/(м с).!
4. кг м /с2.
|
|
Какая из перечисленных физических величин имеет размерность м2/с?
|
1. Коэффициент теплопроводности.
2. Коэффициент диффузии.
3. Ускорение.
4. Коэффициент вязкости.!
|
|
Единица измерения коэффициента теплопроводности?
|
1. Па∙с.
2. Вт/(м·К).!
3. Дж/с.
4. Вт/(м·с).
|
1.2.Б. Погрешности измерений физических величин (базовые вопросы)
|
|
Среднеквадратичная ошибка результата серии nпрямых измерений физической величины d вычисляется по формуле:
|
1. 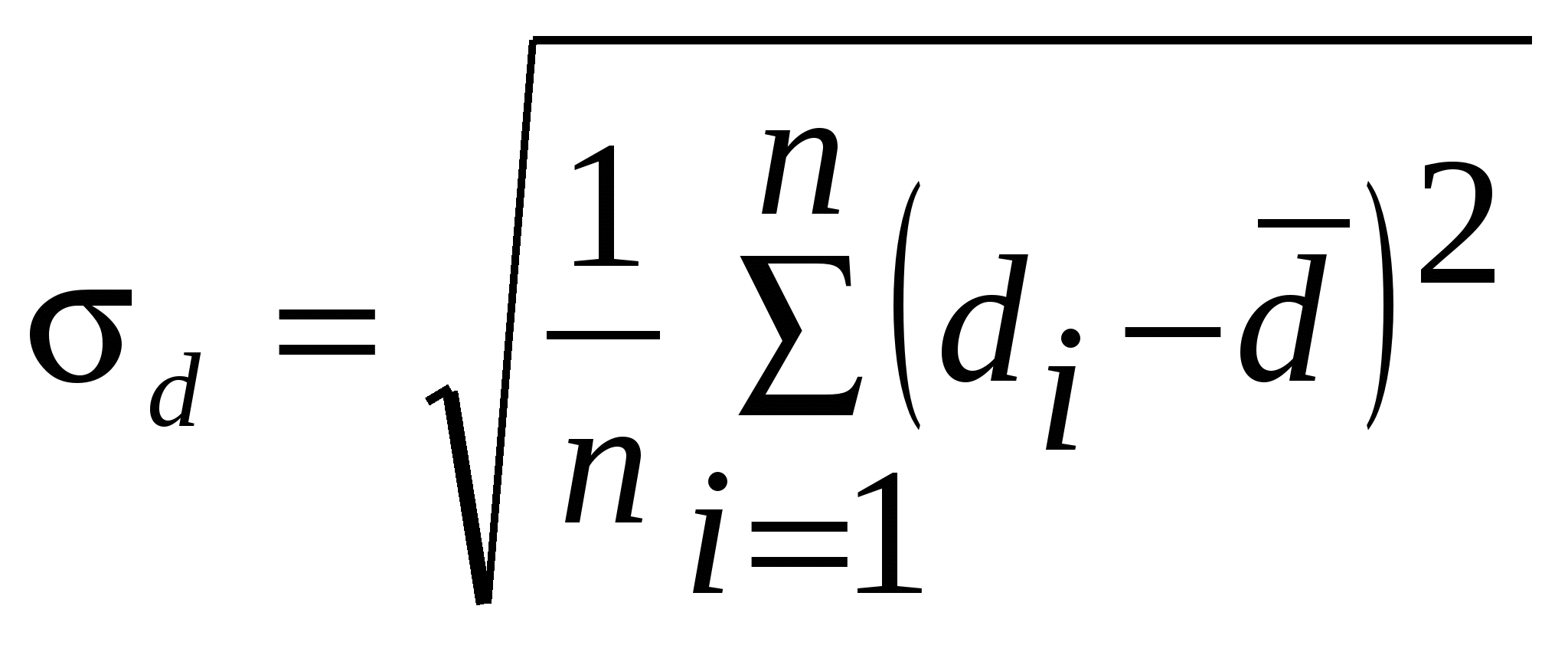 . .
2. 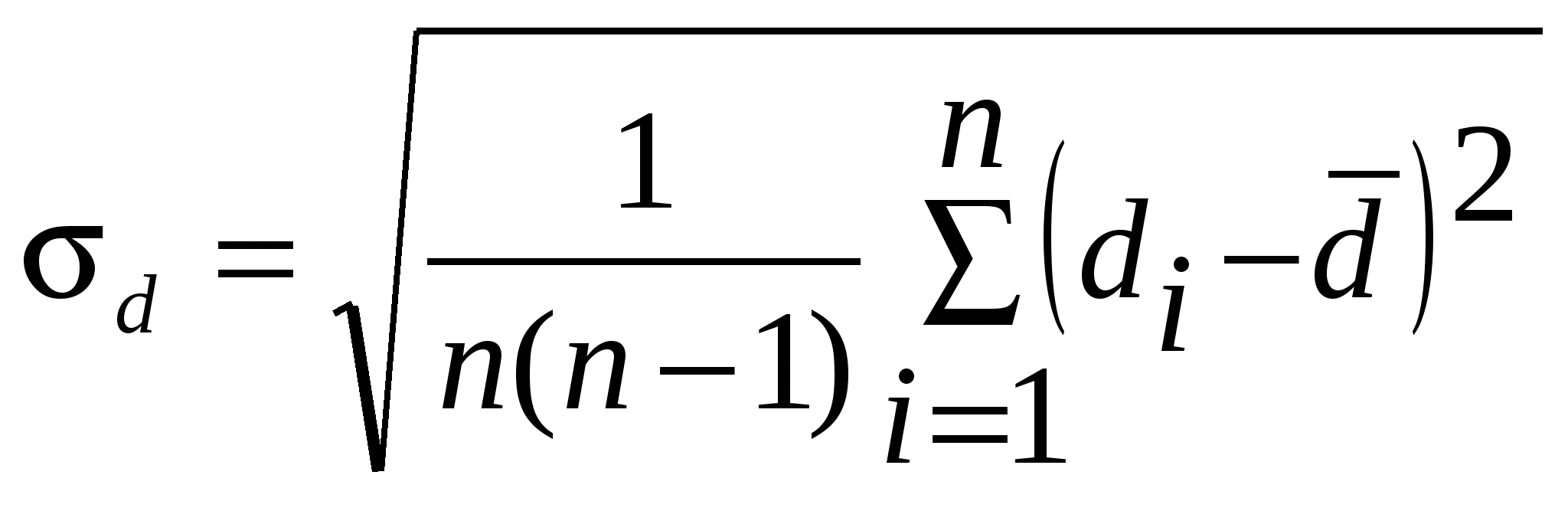 .! .!
3. 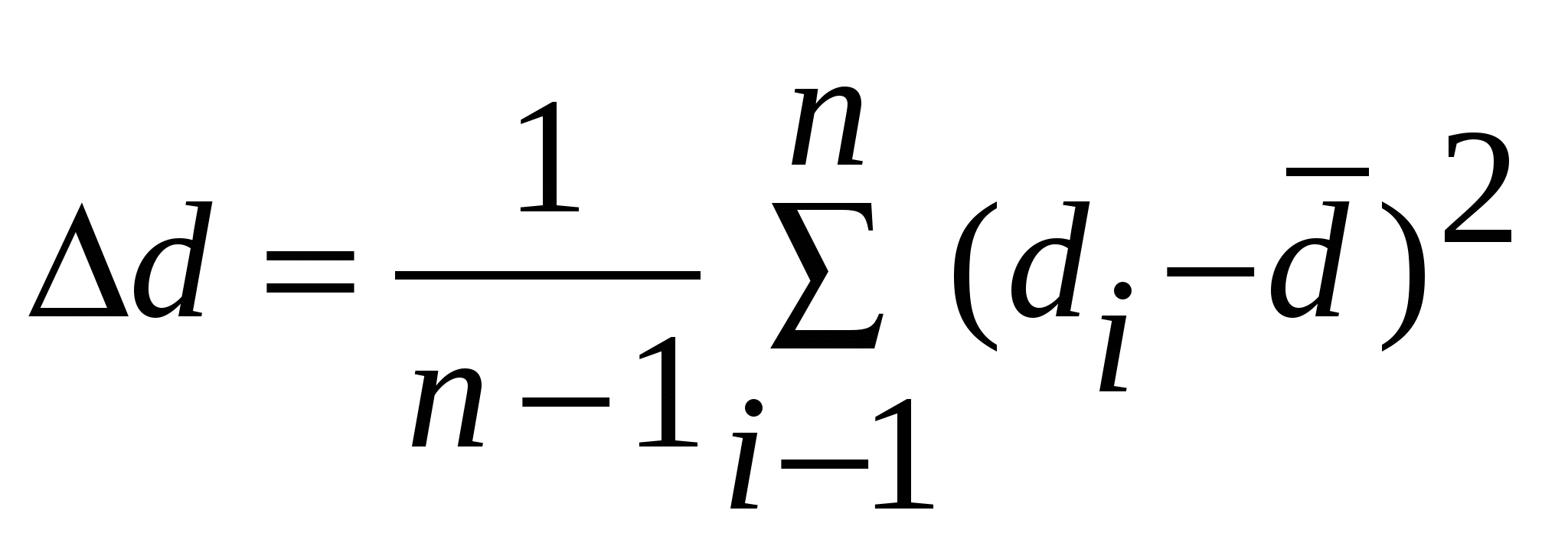 . .
4. 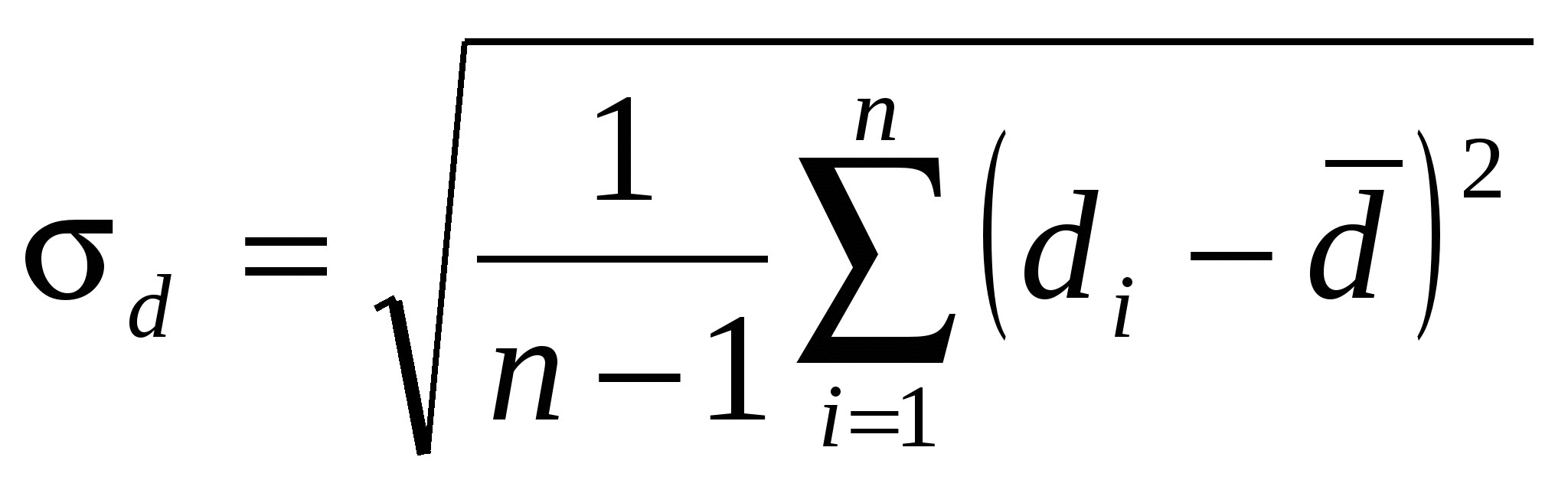 . .
|
|
Средняя квадратичная ошибка результата n прямых измерений физической величины d вычисляется по формуле:
|
1. 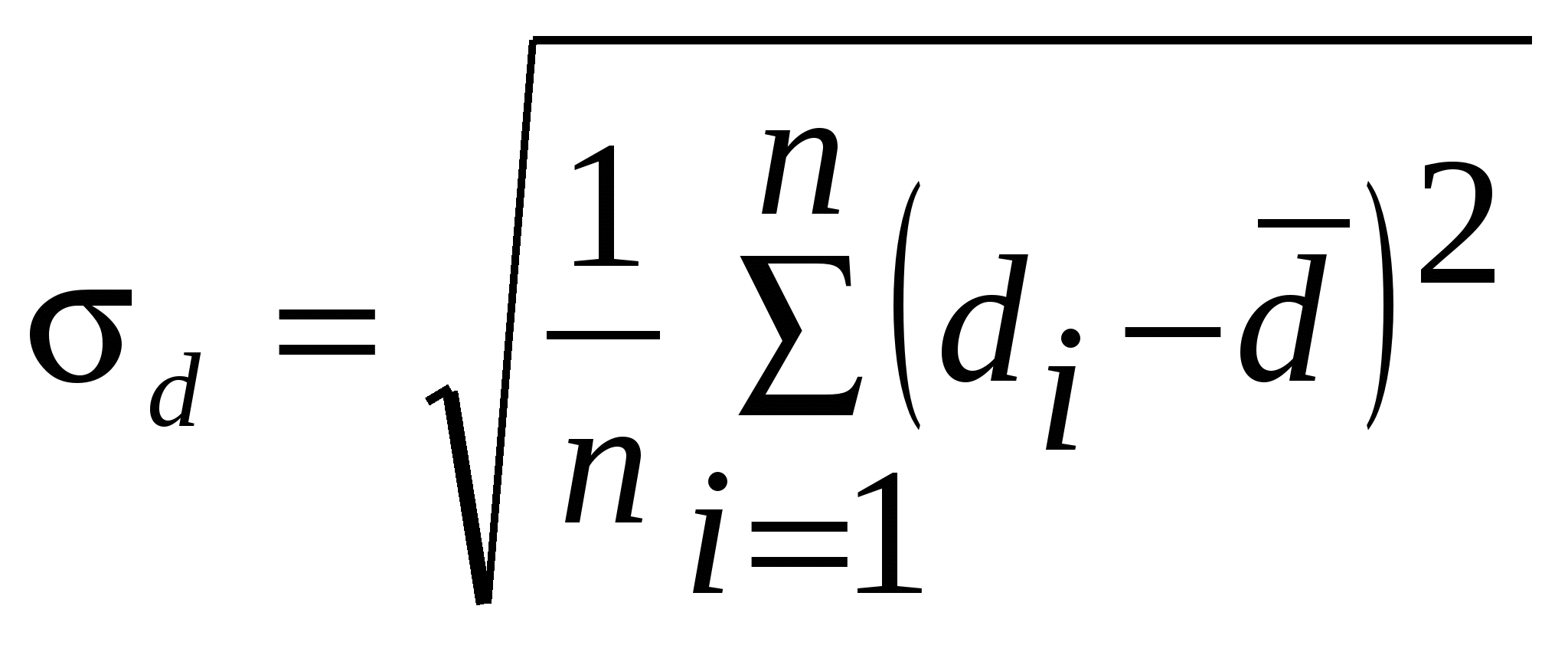 . .
2. 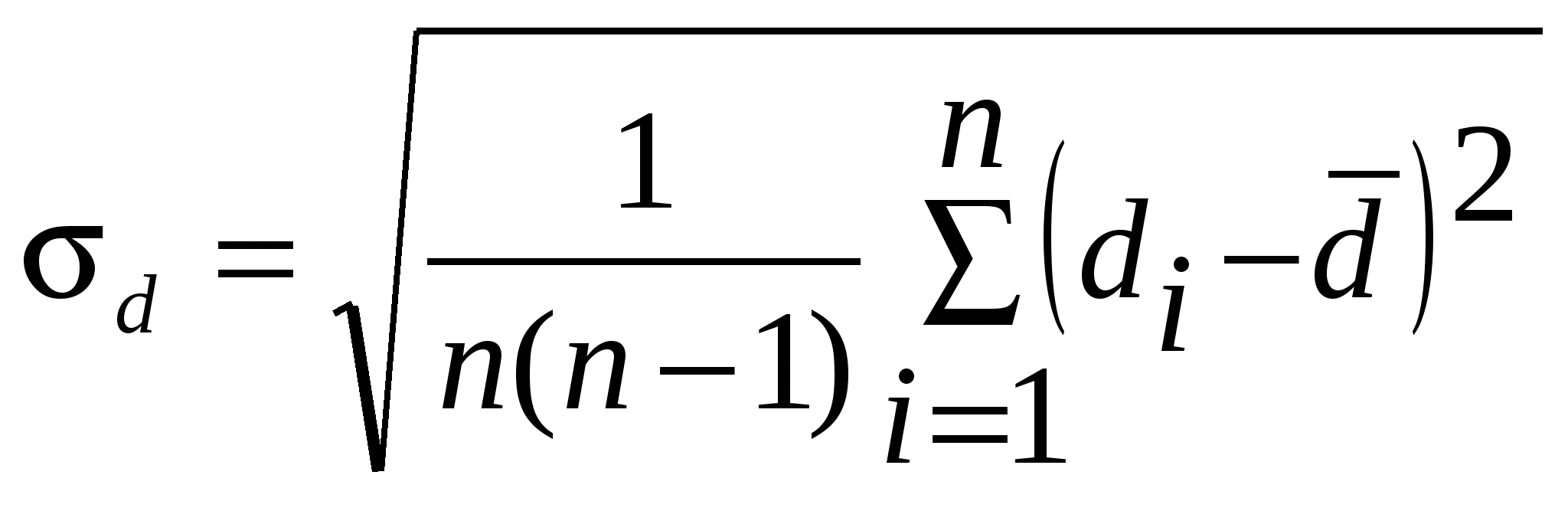 . .
3. 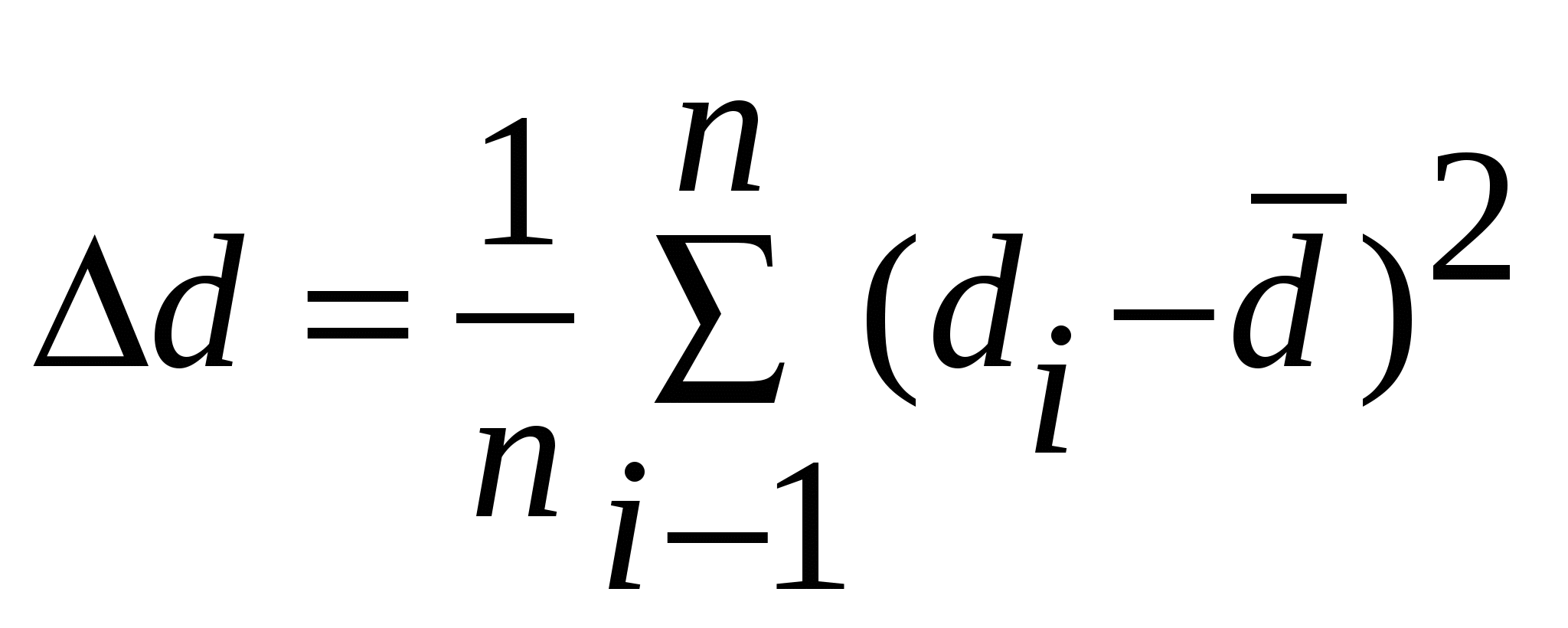 . .
4. 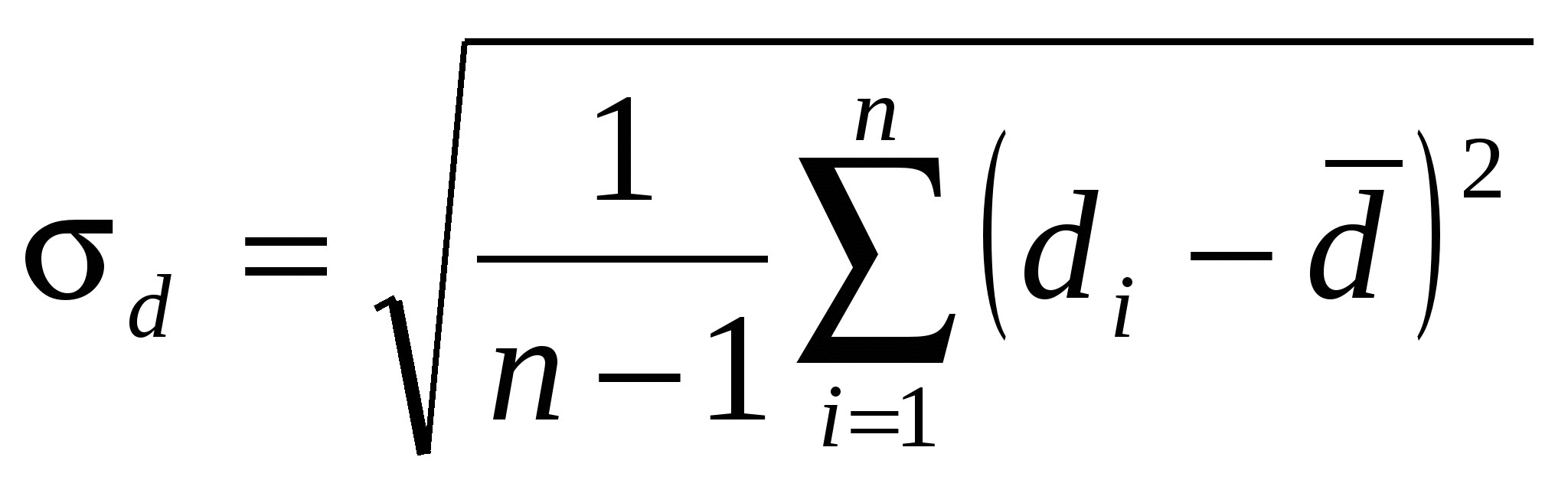 .! .!
|
|
Средняя абсолютная погрешность результата n прямых измерений физической величины х определяется по формуле:
|
1. 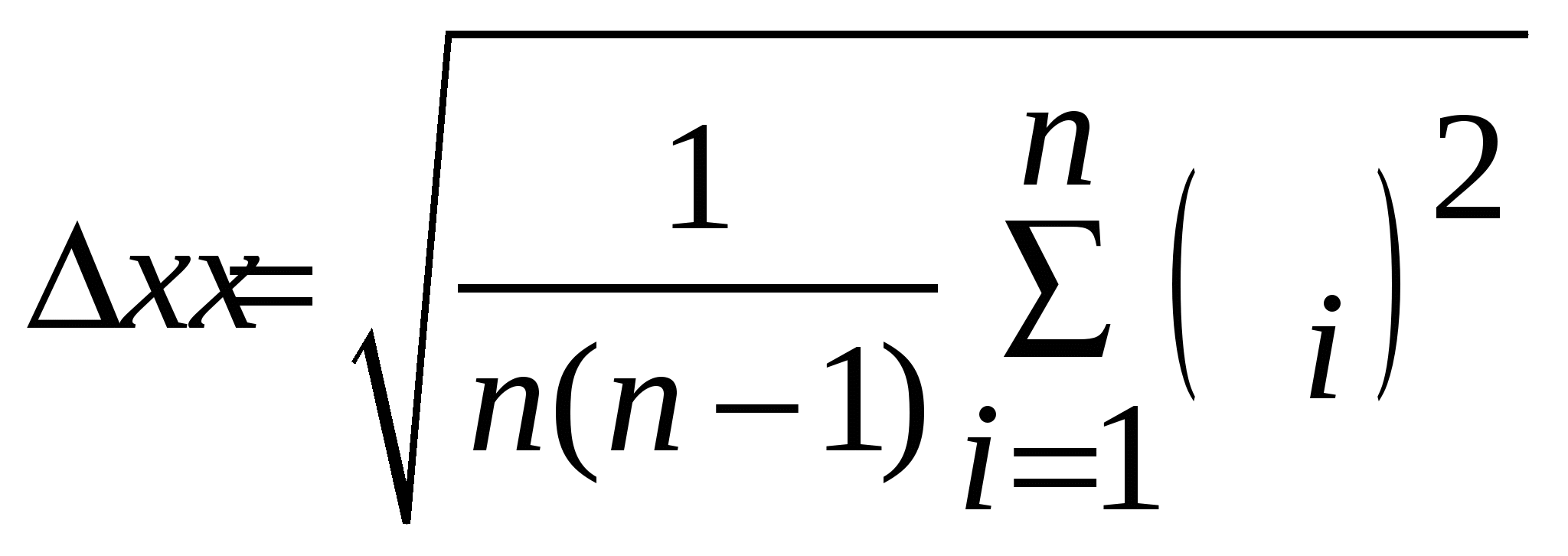 . .
2. 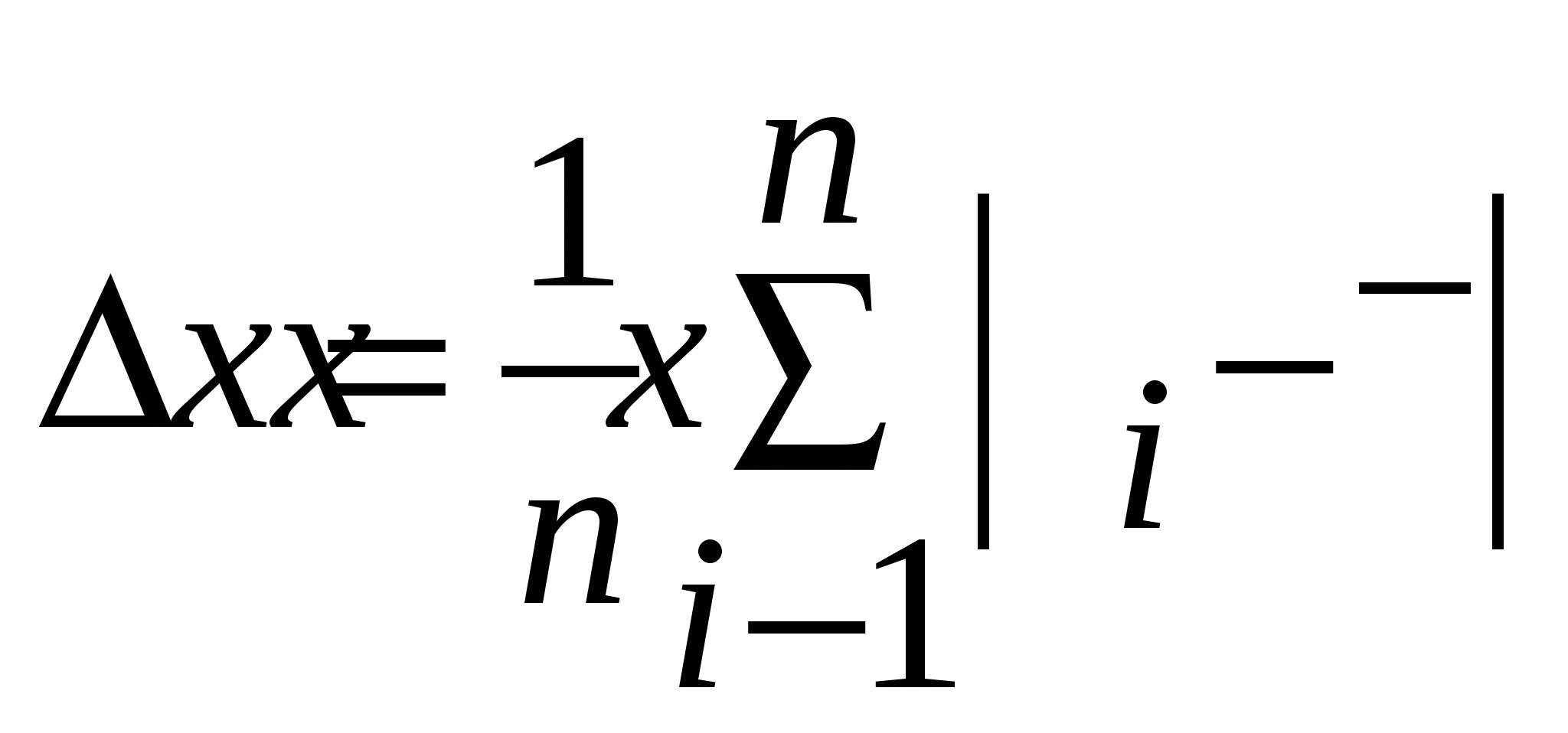 .! .!
3. 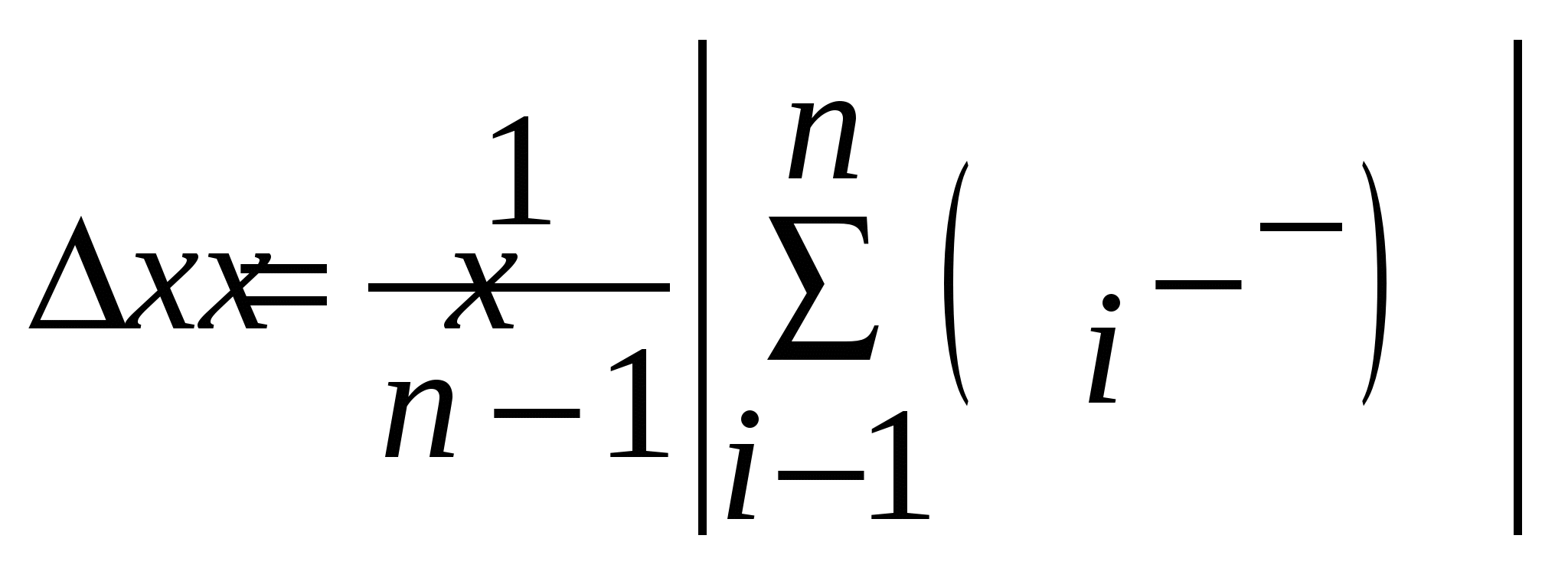 . .
4. 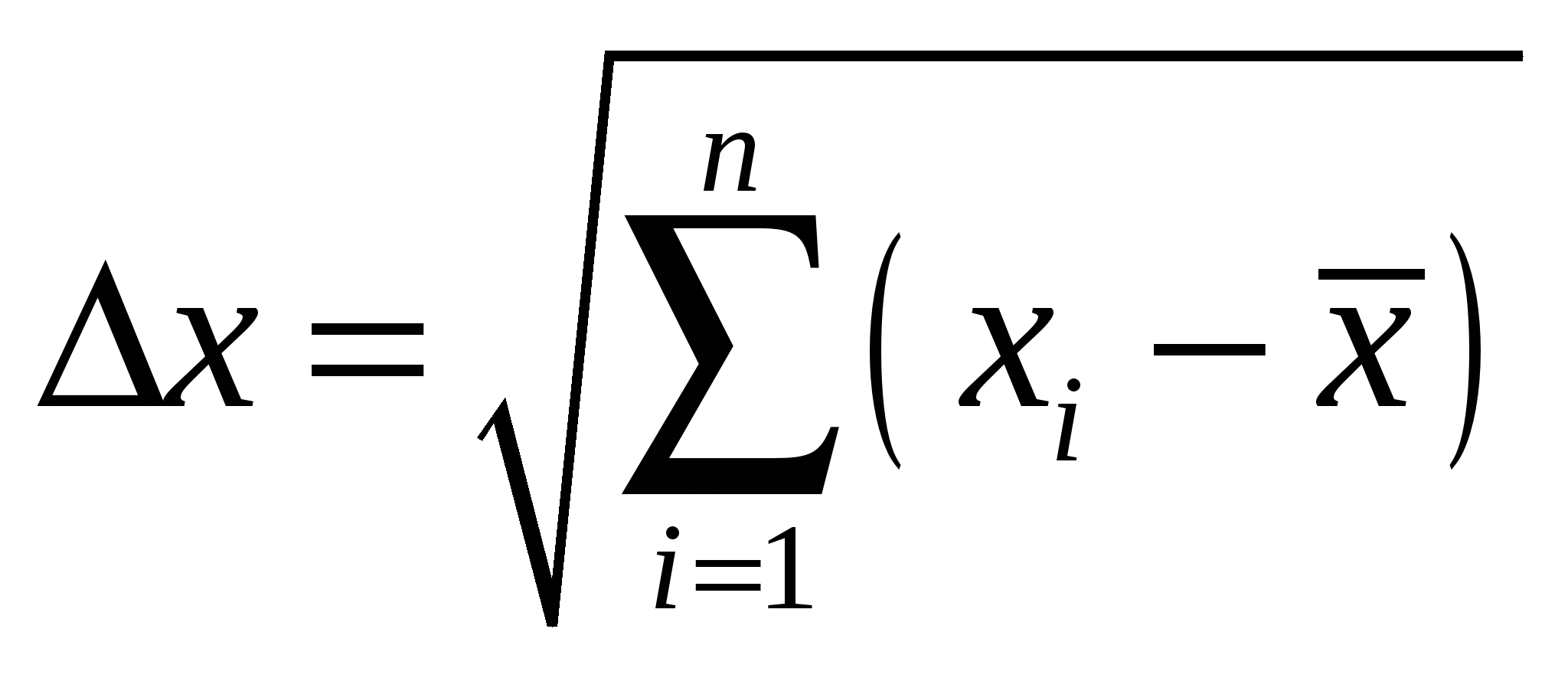 . .
|
|
Во сколько раз отличаются среднеквадратичная погрешность n прямых измерений 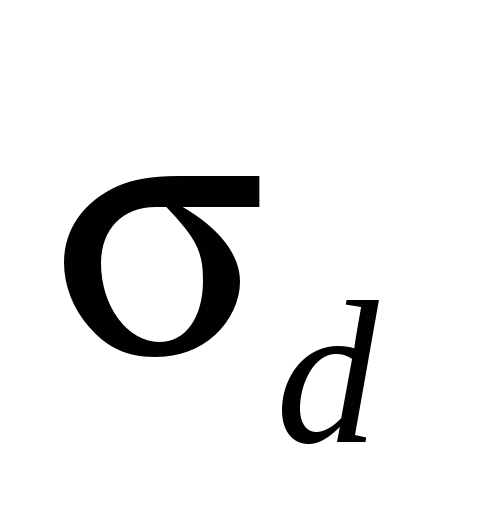 физической величины d от среднеквадратичной погрешности физической величины d от среднеквадратичной погрешности 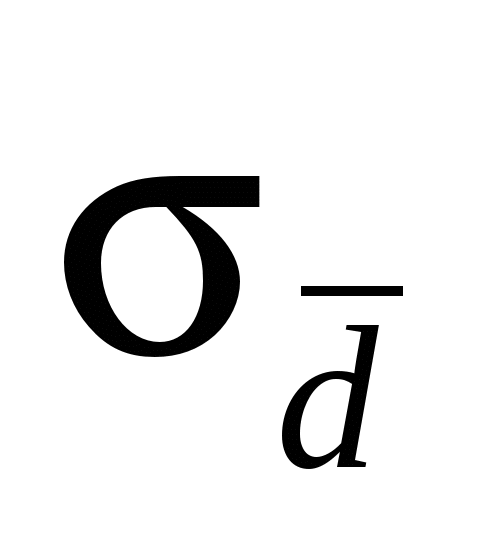 прямых измерений среднего значения этой величины? прямых измерений среднего значения этой величины?
|
1. 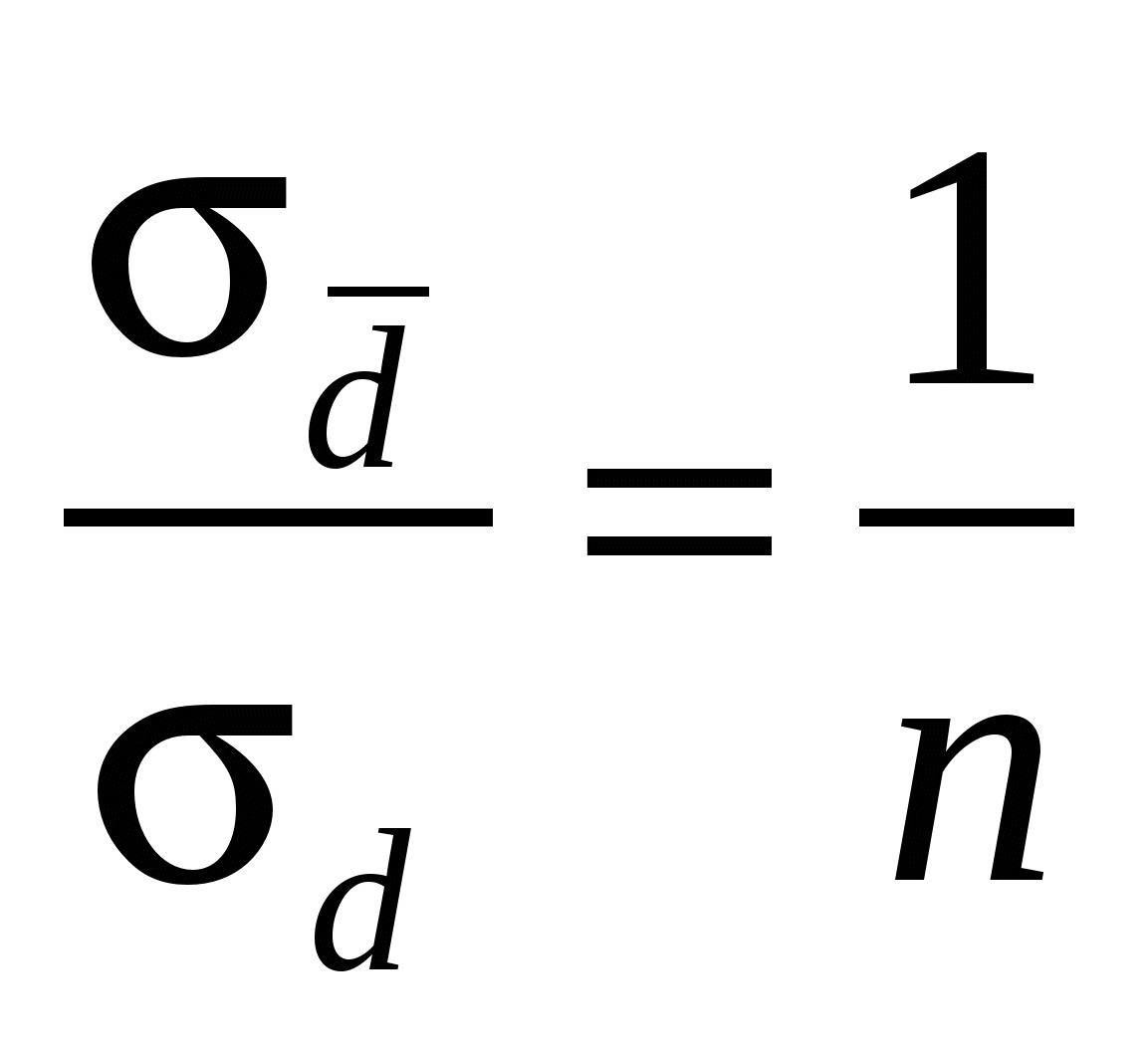 . .
2. 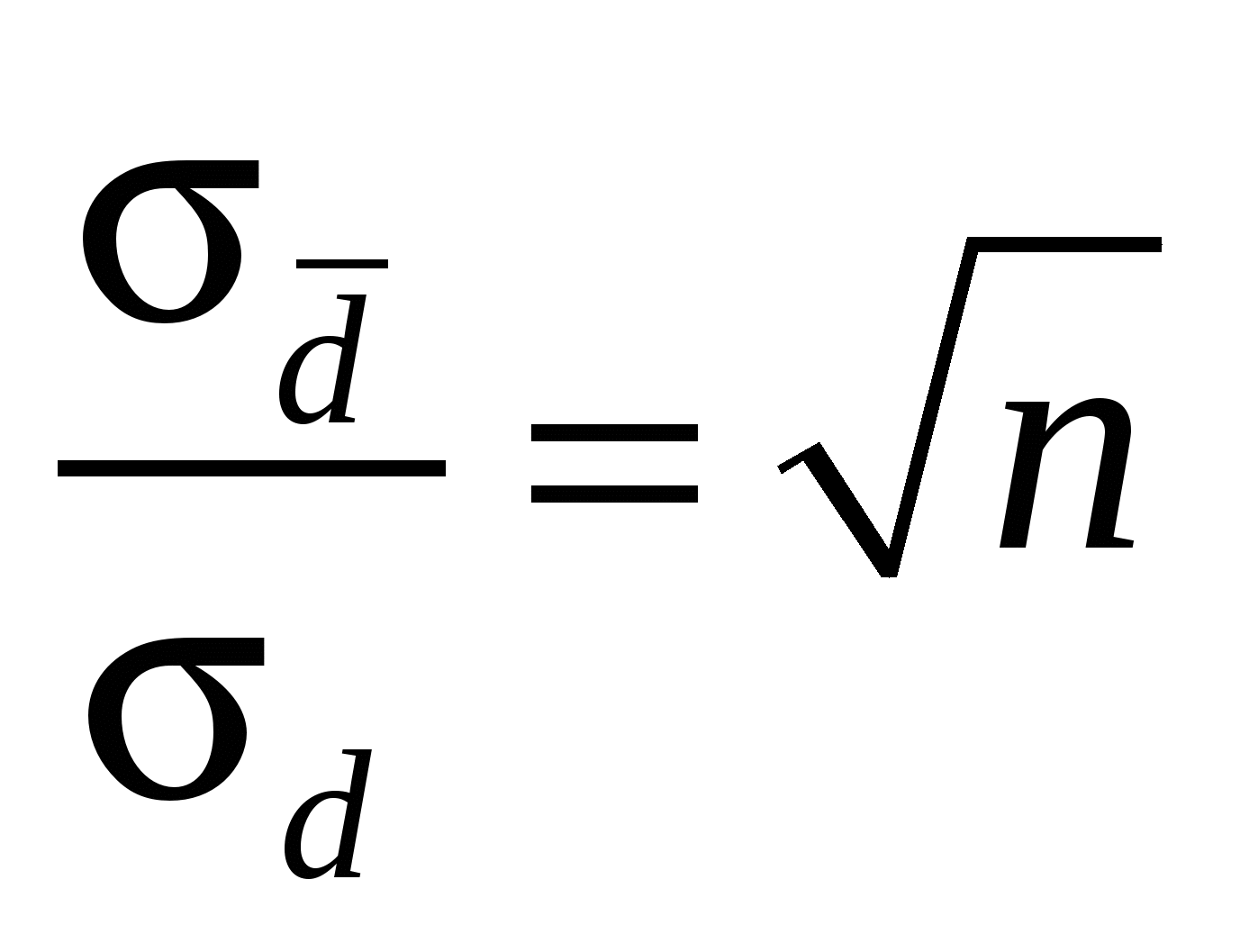 . .
3. 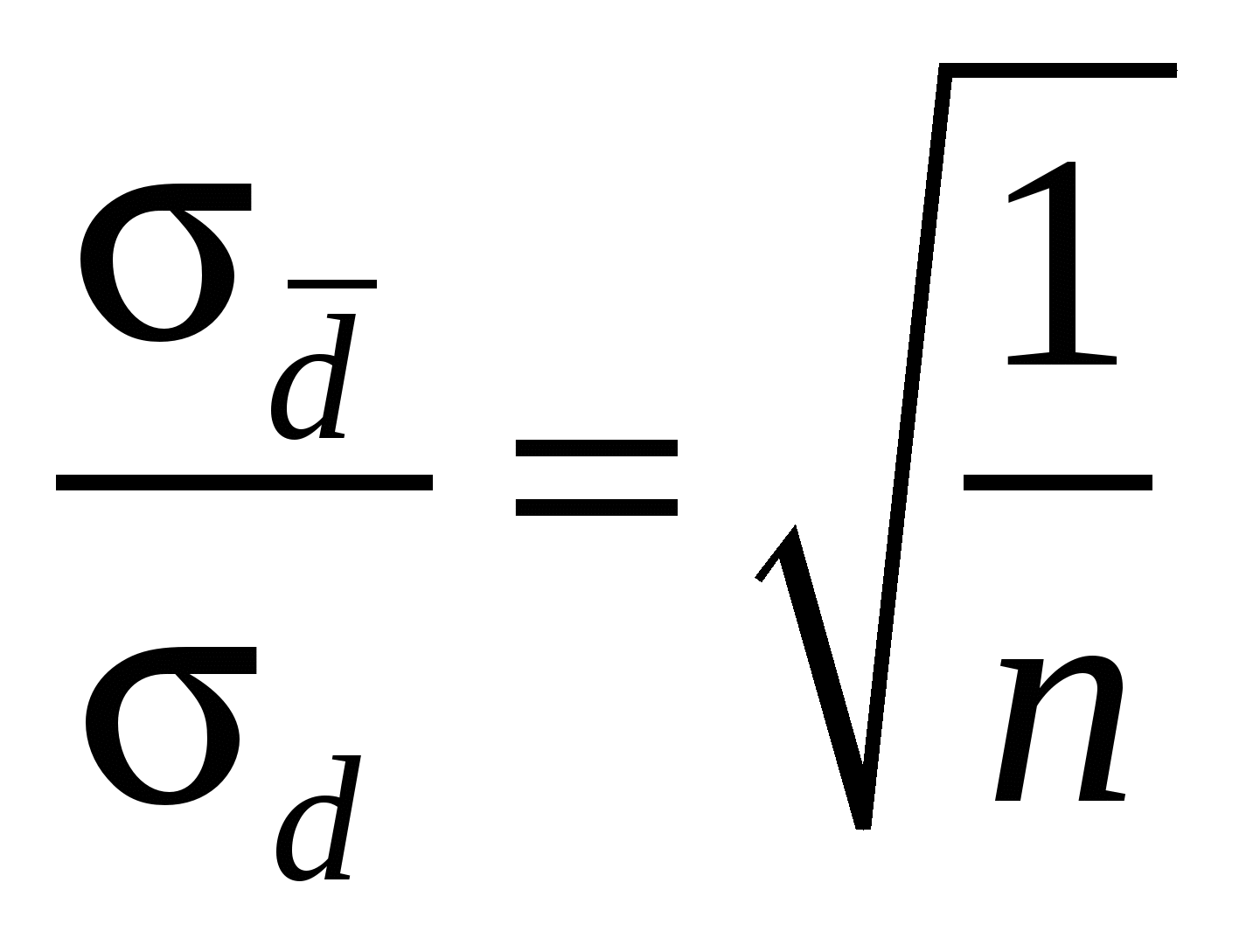 .! .!
4. 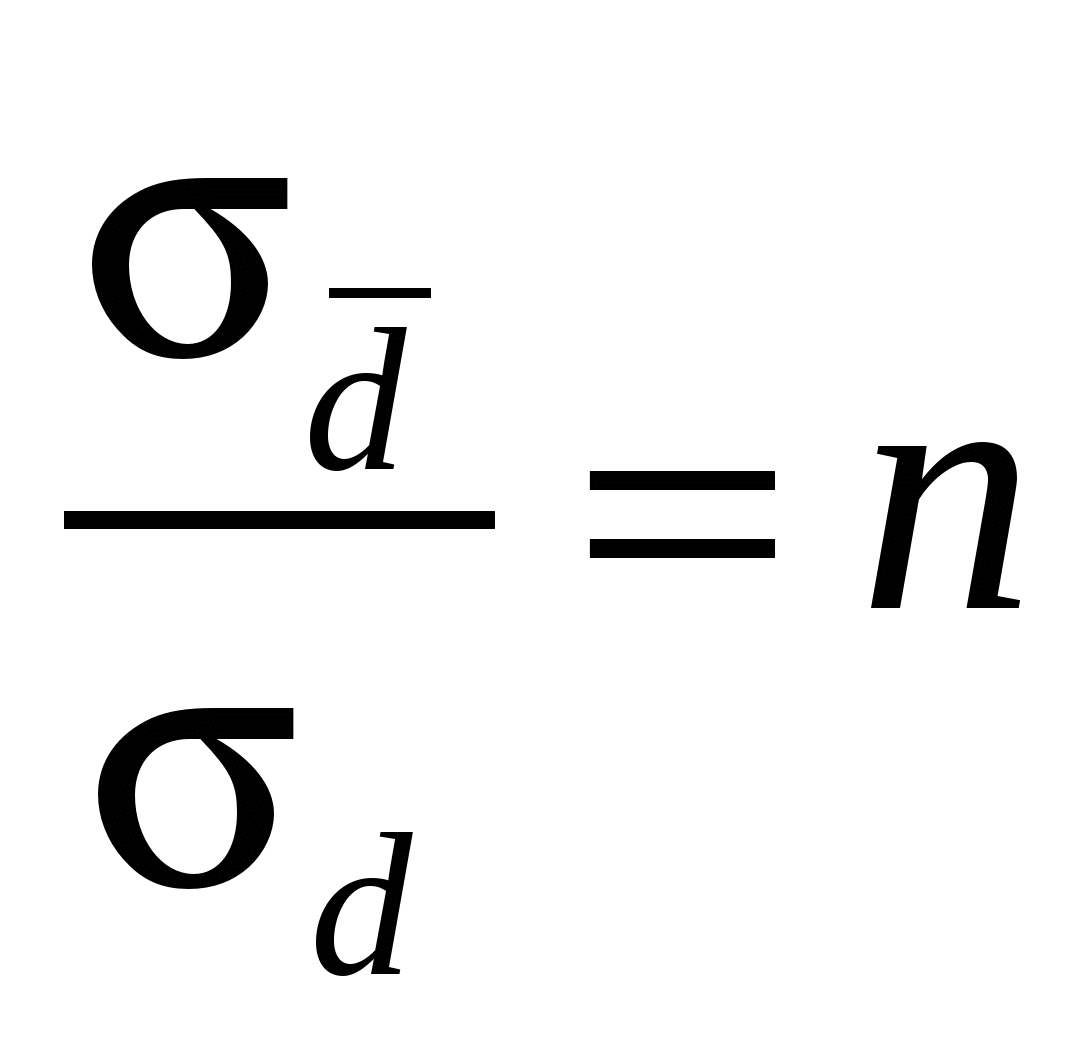 . .
|
|
Укажите классификационный признак, лежащий в основе разделения погрешностей измерений на абсолютные и относительные.
|
1. Источники возникновения.
2. Условия изменения измеряемой величины.
3. Способ выражения.!
4. Способ обработки ряда изменений.
|
|
Выражение для косвенного измерения физической величины (объёма цилиндра)
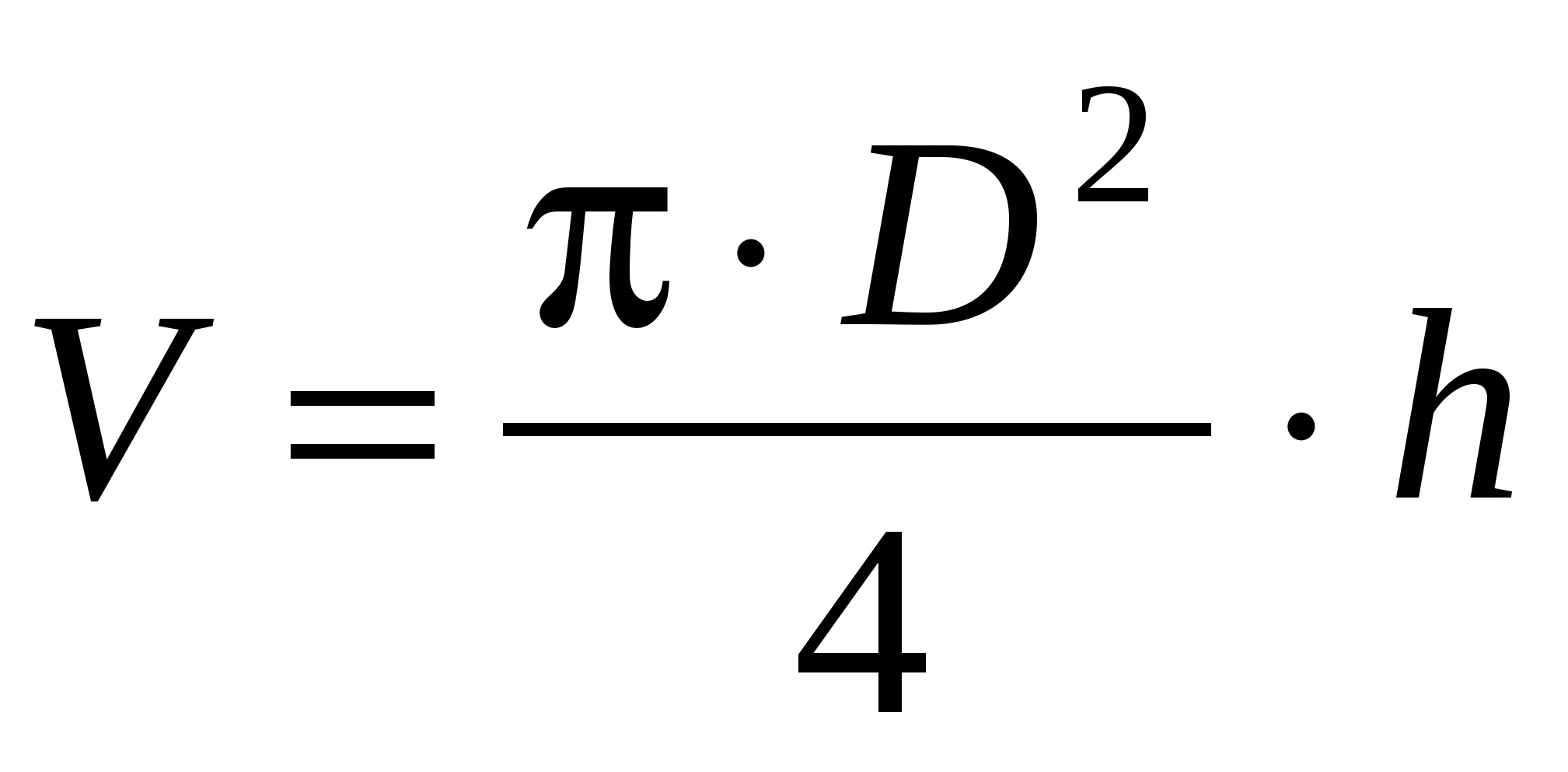
Величина диаметра D и высоты цилиндра h измеряются непосредственно приборами с погрешностями прямых измерений соответственноD и h
Максимальная относительная погрешность косвенных измерений объёма цилиндра…
|
1. 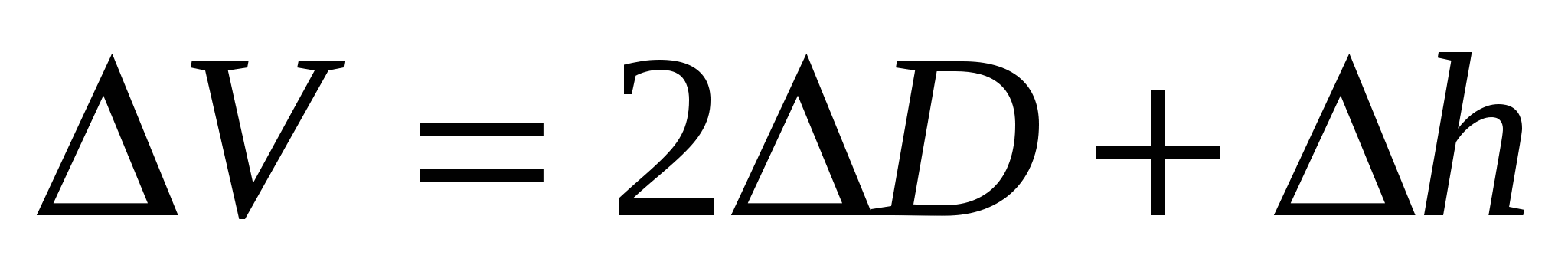 . .
2. 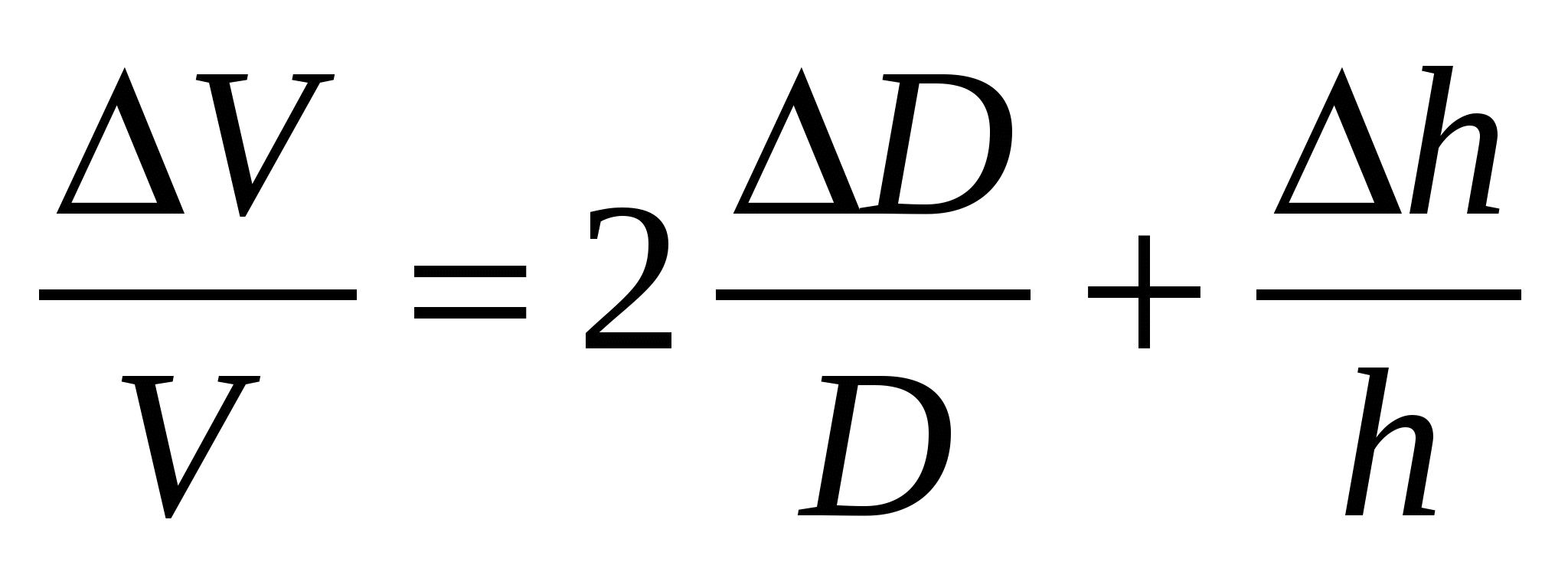 .! .!
3. 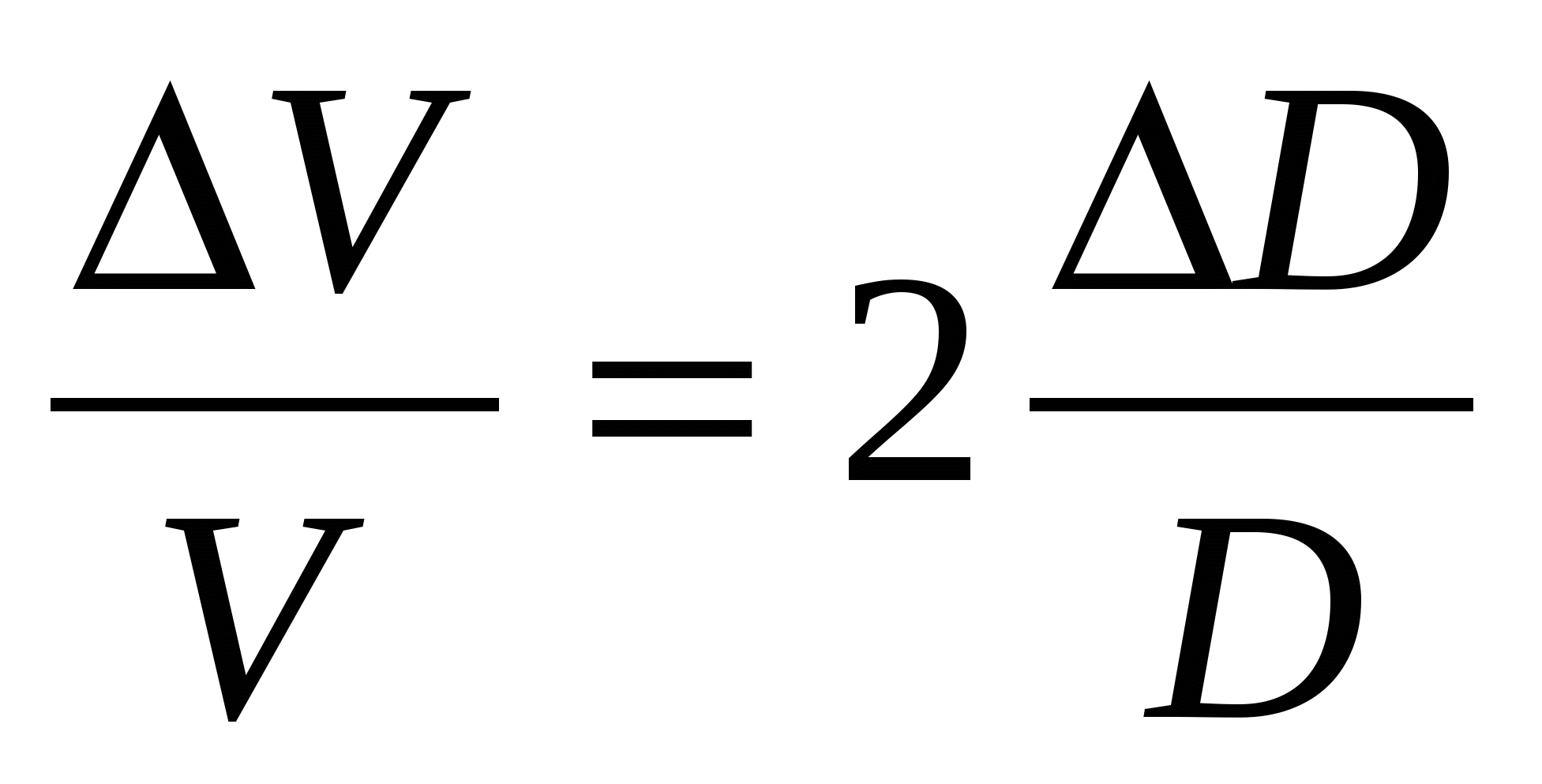 . .
4. 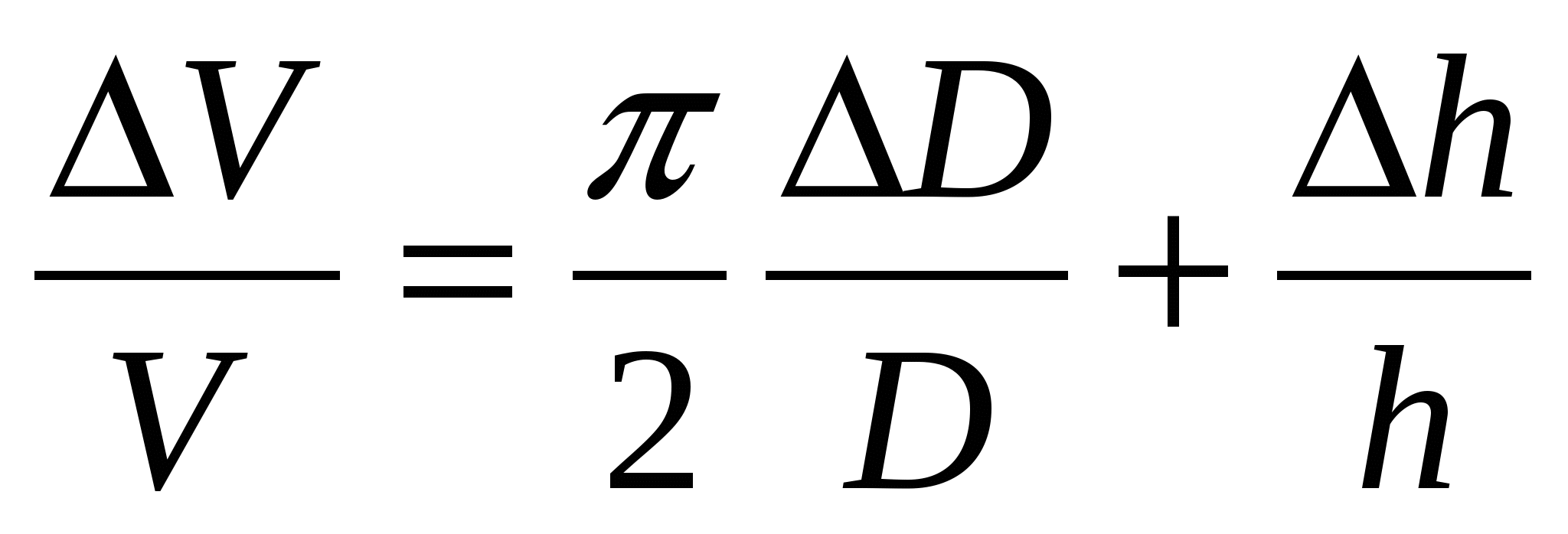 . .
|
|
Объём конуса рассчитывается по формуле: 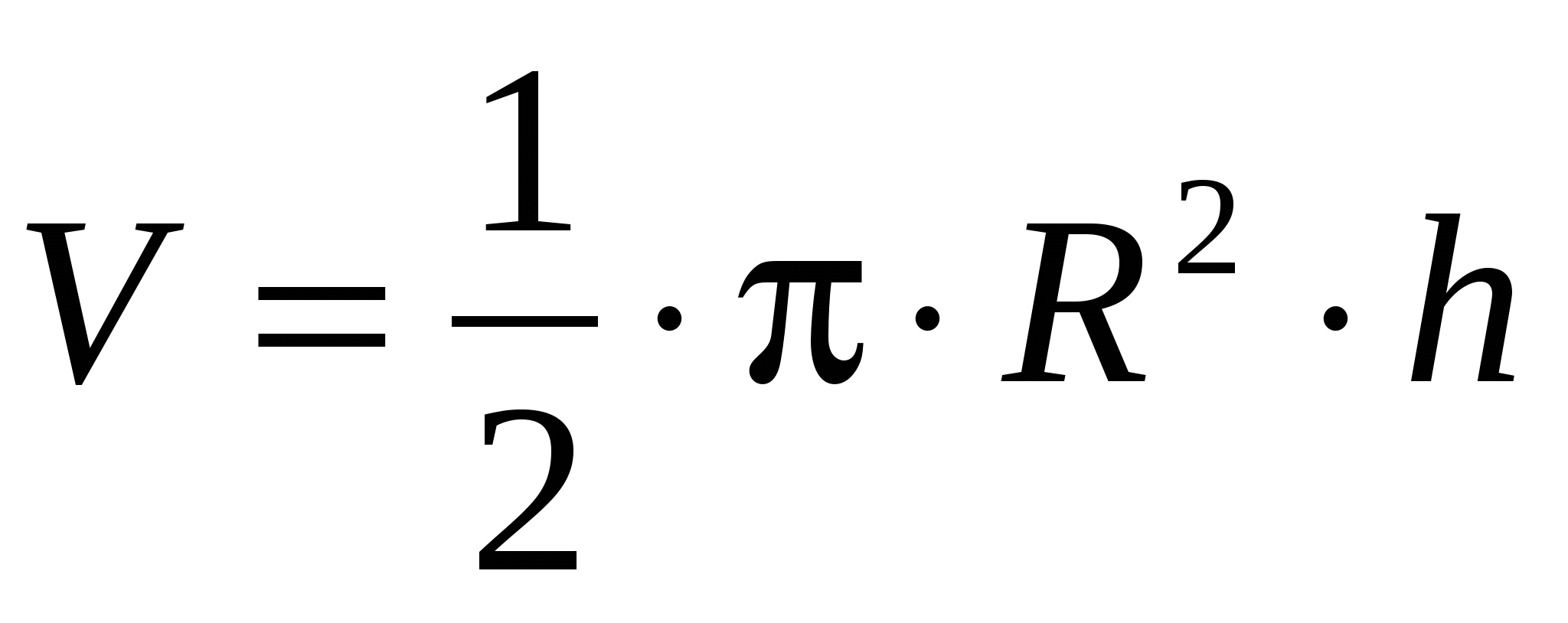 , ,
Максимальная относительная погрешность косвенных измерений объёма конуса равна…
( R, R,  h – погрешности прямых измерений, – постоянная, R – радиус конуса, h – высота конуса). h – погрешности прямых измерений, – постоянная, R – радиус конуса, h – высота конуса).
|
1. 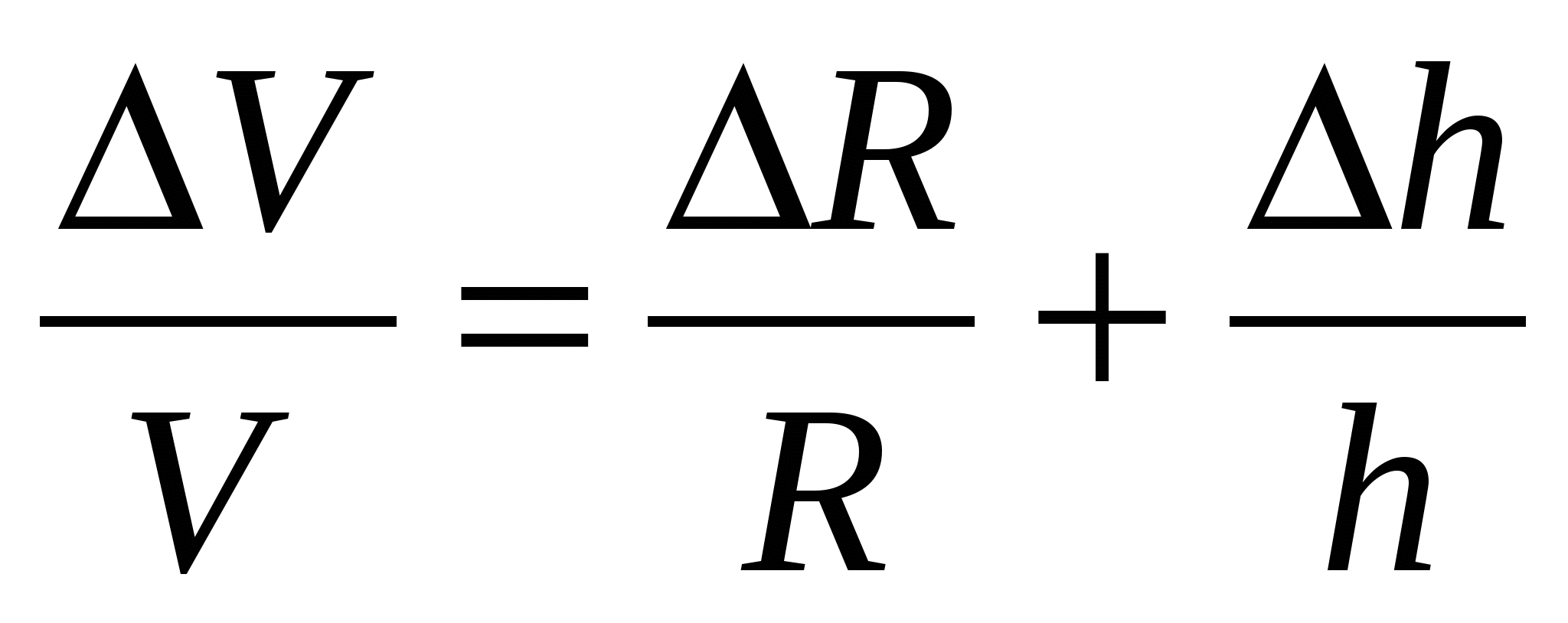 . .
2. 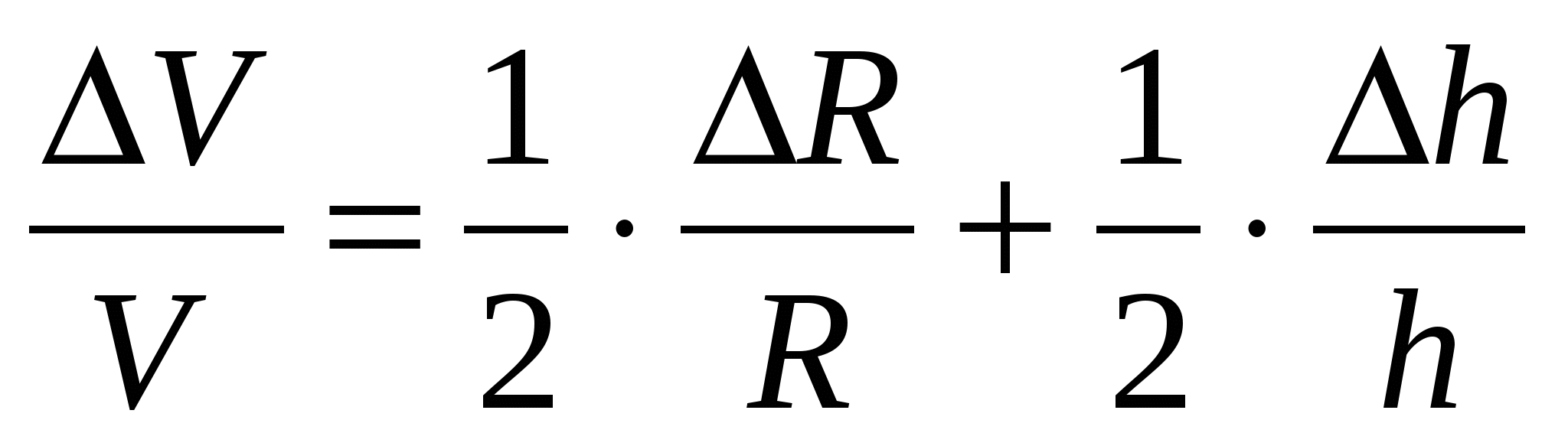 . .
3. 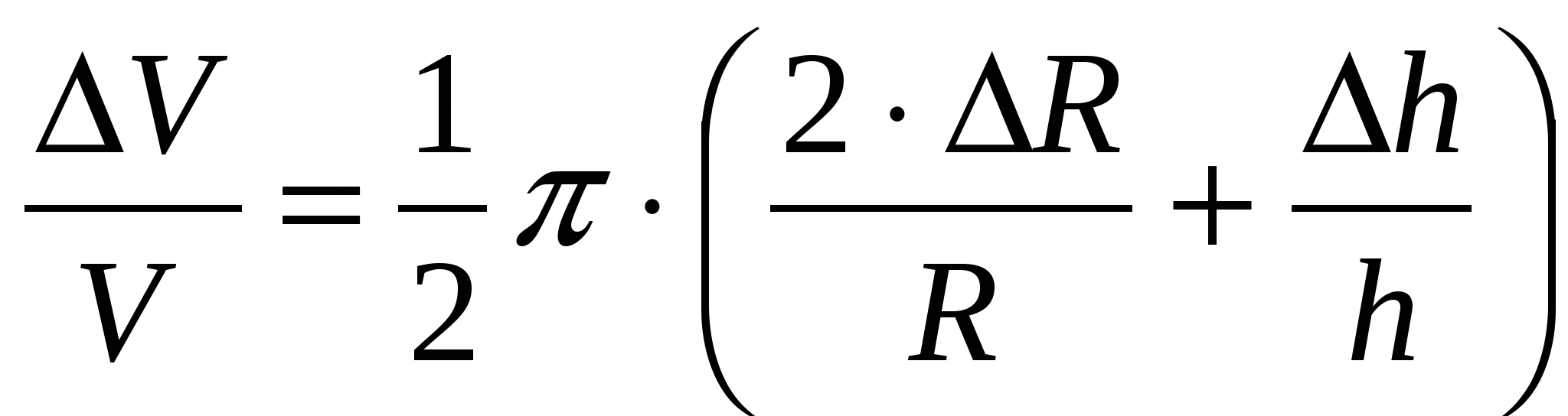 . .
4. 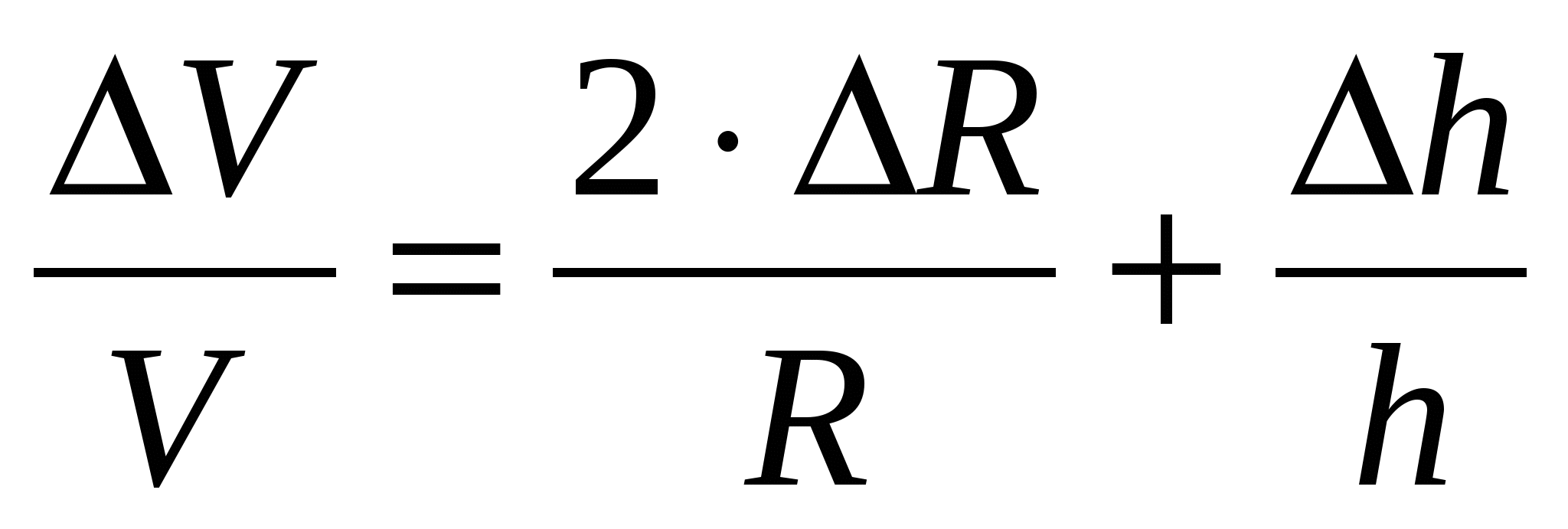 .! .!
|
2. Механика
|
2.1. Б. Кинематика материальной точки (базовые вопросы)
|
|
Движение некоторой точки описывается уравнением: 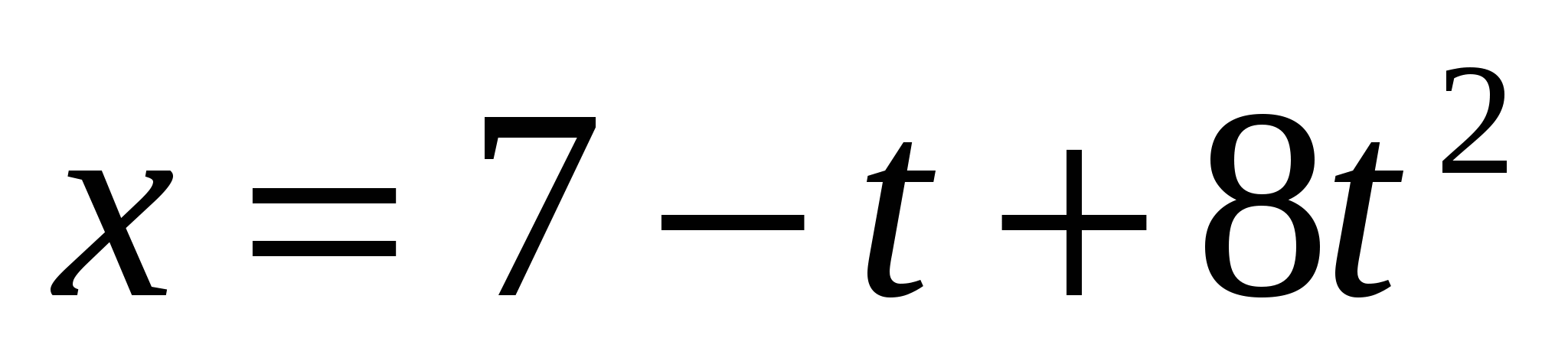 , м. Какое из приведенных выражений соответствует зависимости проекции скорости этого тела от времени? , м. Какое из приведенных выражений соответствует зависимости проекции скорости этого тела от времени?
|
1. 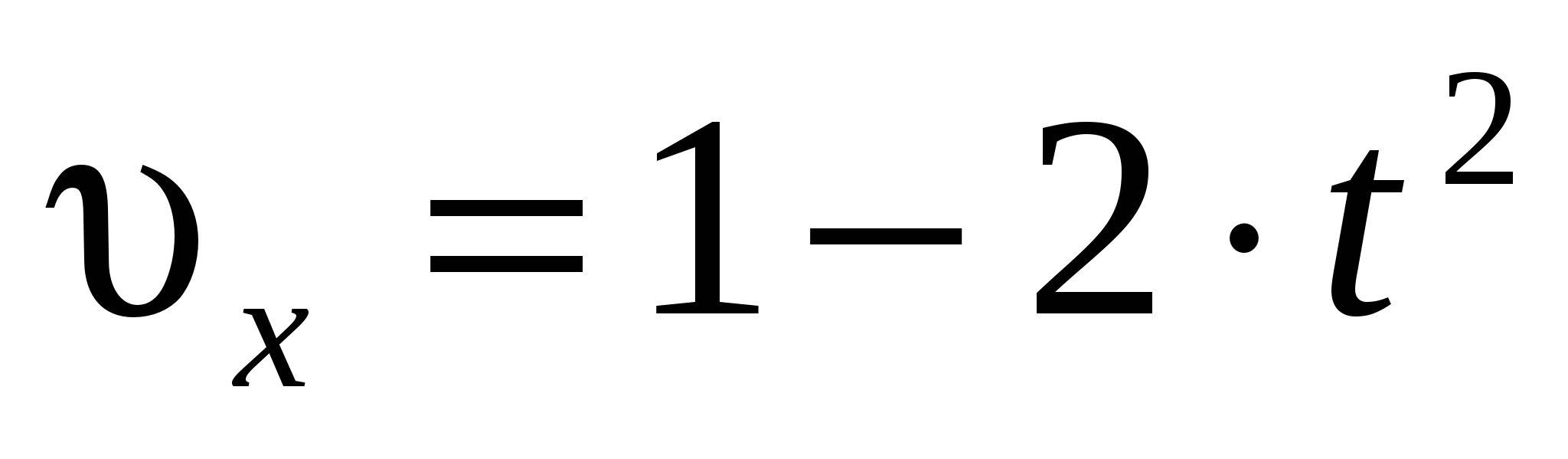 , м/с. , м/с.
2. 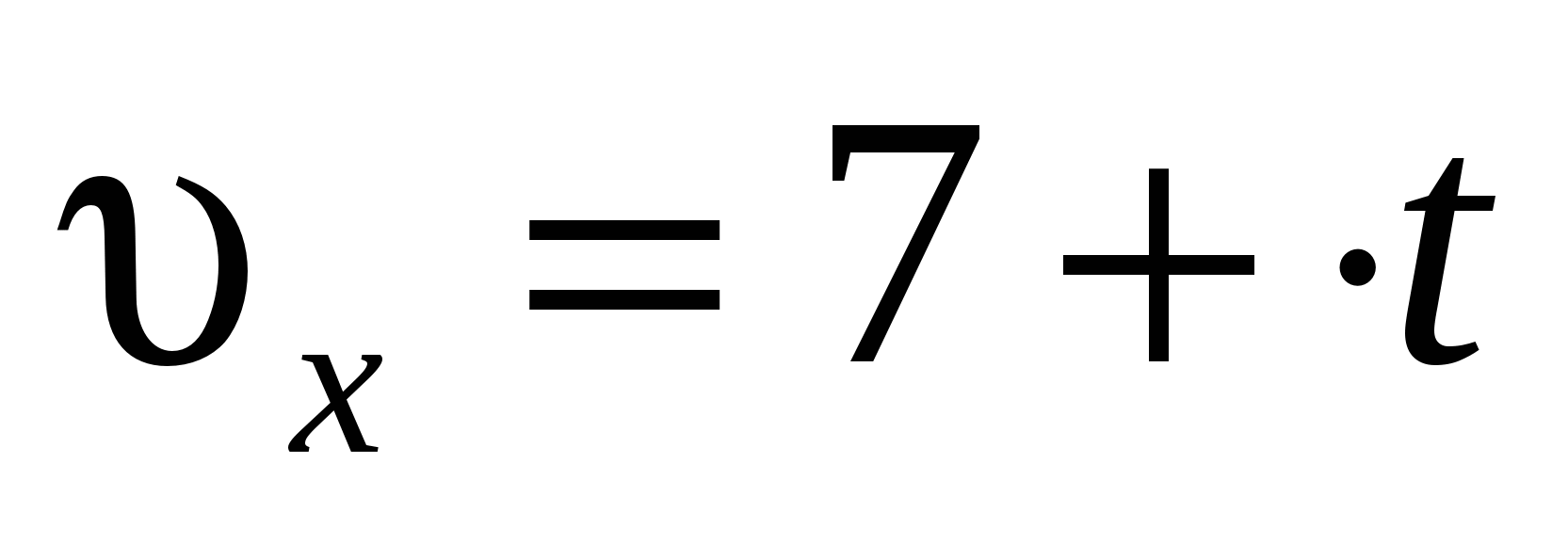 , м/с. , м/с.
3. 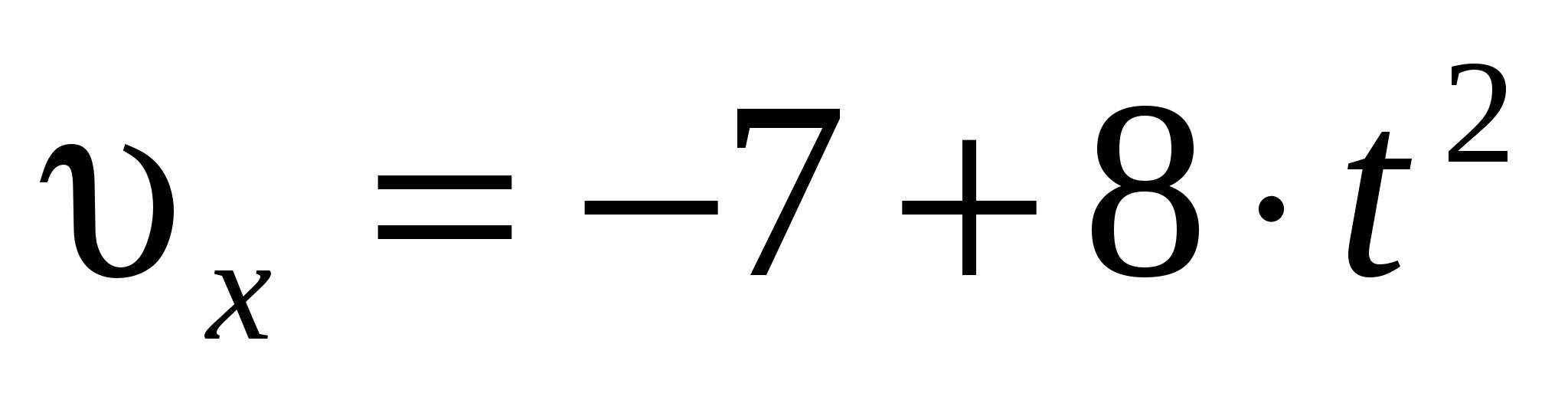 , м/с. , м/с.
4. 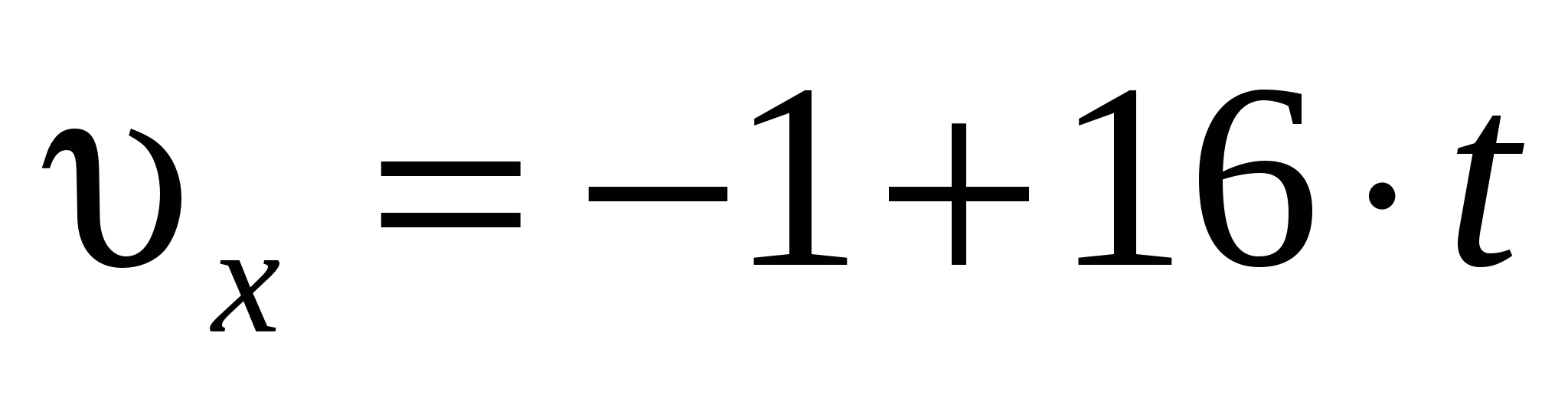 , м/с.! , м/с.!
|
|
Если a = 0 и an 0, то такое движение называется…
(a – тангенциальное ускорение, an– нормальное ускорение)
|
1. равномерное криволинейное.!
2. прямолинейное равномерное.
3. прямолинейное равнопеременное.
4. криволинейное равнопеременное.
|
| При прямолинейном движении зависимость пройденного телом пути от времени задана уравнением: S = 4 + 15t2 + t3. Как при этом изменяется модуль скорости? |
1. Убывает.
2. Проходит через минимум.
3. Возрастает.!
4. Остаётся постоянным.
|
|
Точка движется по расширяющейся спирали (см. рис.) так, что ее нормальное ускорение аn = const. Как изменяются при этом линейная и угловая скорости?
EMBED PBrush 
|
1. Линейная увеличивается, а угловая убывает.
2. Угловая увеличивается, а линейная убывает.!
3. Скорости обе увеличиваются пропорционально корню квадратному из радиуса кривизны спирали.
4. Скорости не изменяются.
|
| Точка движется по расширяющейся спирали (см. рис.) так, что ее модуль скорости υ = const. Как изменяются при этом нормальное и тангенциальное ускорение?
EMBED PBrush 
|
1. Нормальное убывает, а тангенциальное увеличивается.
2. Тангенциальное не изменяется, а нормальное убывает.!
3. Оба увеличиваются пропорционально корню квадратному из радиуса кривизны спирали.
4. Оба увеличиваются пропорционально квадрату радиуса кривизны спирали.
|
|
Компоненты ускорения в декартовой системе координат равны…
|
1. первым производным соответствующих координат по времени.
2. вторым производным соответствующих координат по времени.!
3. соответствующим координатам декартовой системы.
4. вторым производным соответствующих компонент скорости.
|
| Для определения положения материальной точки в заданной системе отсчета необходимо задать… |
1. радиус-вектор этой точки.!
2. тело отсчета.
3. ускорение точки.
4. скорость точки.
|
|
Координаты точки, движущейся в плоскости XY, изменяются по закону:
X = –2t; Y = 4t.
Траектория движения……
|
1. эллипс.
2. прямая линия, проходящая через вторую и четвертую четверть.
3. прямая линия, проходящая через первую и третью четверть.!
4.гипербола.
|
|
Модуль ускорения характеризует быстроту изменения…
|
1. перемещения.
2. скорости.!
3. пути.
4. направления движения.
|
|
Кинематические уравнения движения точки представлены в виде: 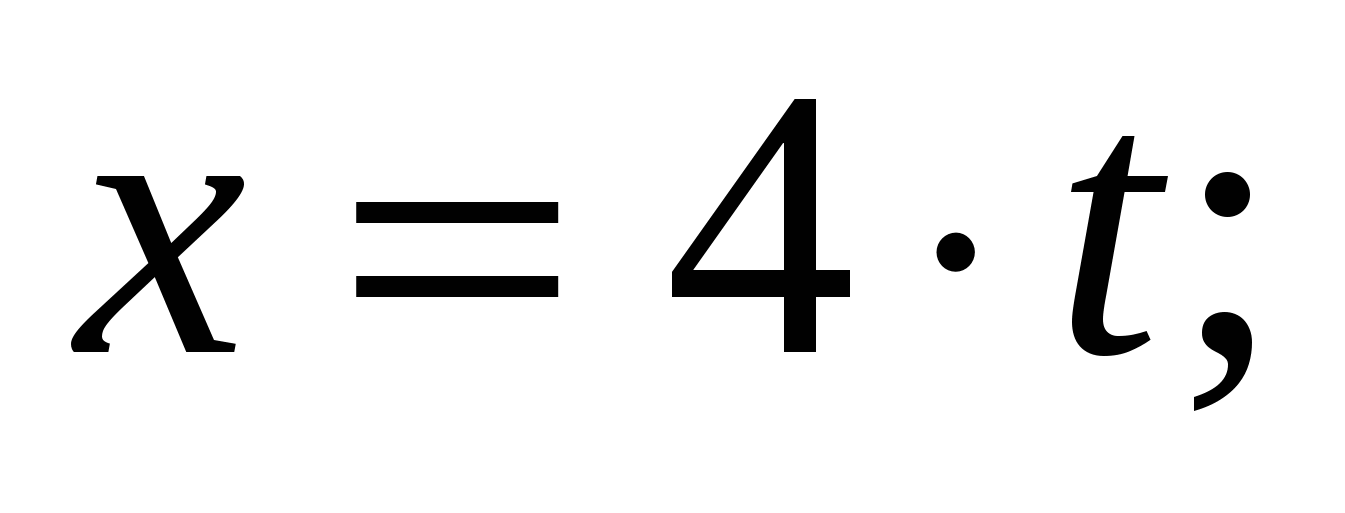 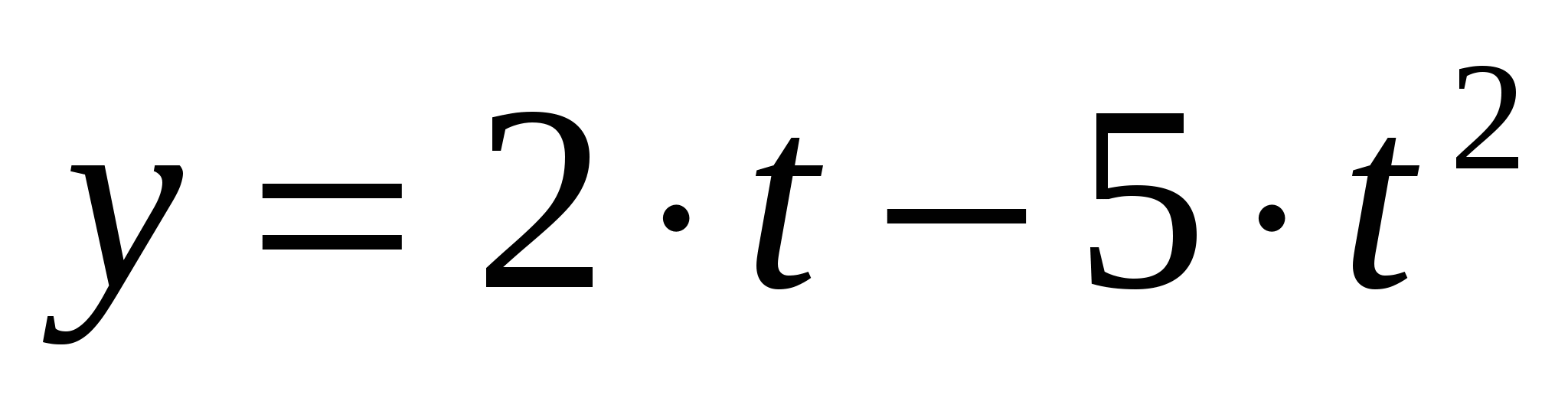 . Скорость точки в момент времени 1 с равна… . Скорость точки в момент времени 1 с равна…
|
1. 4 м/с.
2. 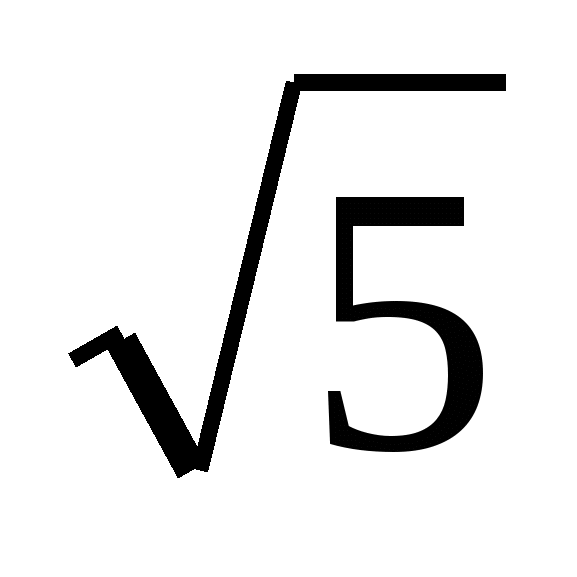 м/c. м/c.
3. 7 м/c.
4. 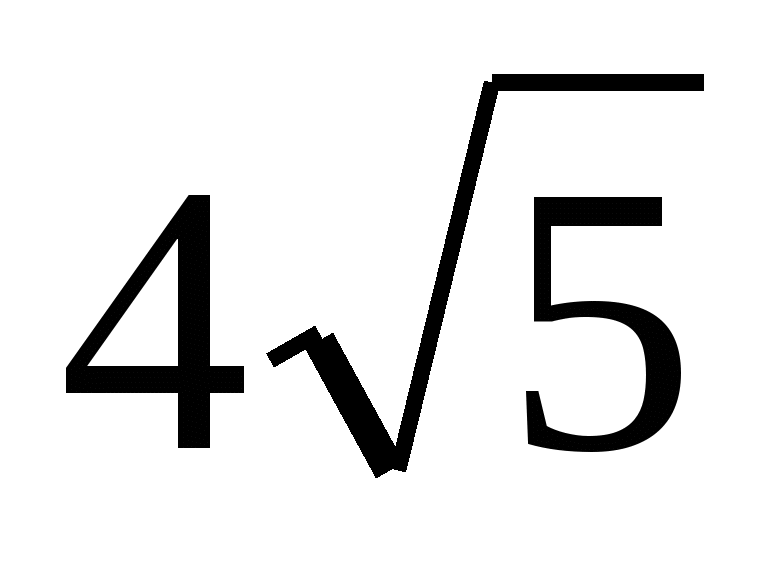 м/c.! м/c.!
|
|
На каком графике правильно изображена зависимость пройденного пути от времени?
|
1.
EMBED PBrush 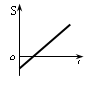
2.
EMBED PBrush 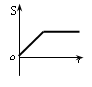 ! !
3.
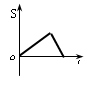
4.
EMBED PBrush 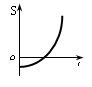
|
|
Для движущейся материальной точки в координатных осях X, Y, Z вторые производные соответствующих составляющих радиус-вектора по времени являются …
|
1. составляющими ускорения этой точки.
2. компонентами скорости этой точки.
3. компонентами ускорения этой точки.!
4. скоростью этой точки.
|
| Зависимость координаты от времени при прямолинейном движении материальной точки задаётся уравнением x = 4 – 15t2. Как при этом меняется модуль ускорения? |
1. Проходит через минимум.
2. Остаётся постоянным.!
3. Монотонно возрастает.
4. Монотонно убывает.
|
| Модуль мгновенной скорости при криволинейном неравномерном движении характеризует … |
1. путь.
2. производную радиус-вектора по времени.
3. перемещение, совершаемое в единицу времени.
4. скорость изменения пути.!
|
|
Для равномерного движения по окружности справедливы соотношения:
(a и an – модули тангенциальной и нормальной составляющих ускорения.)
|
1. a 0, an = const.
2. a = 0, an = 0.
3. a = 0, an = const.!
4. a = 0, an const.
|
|
Угловая скорость вращения – это …
(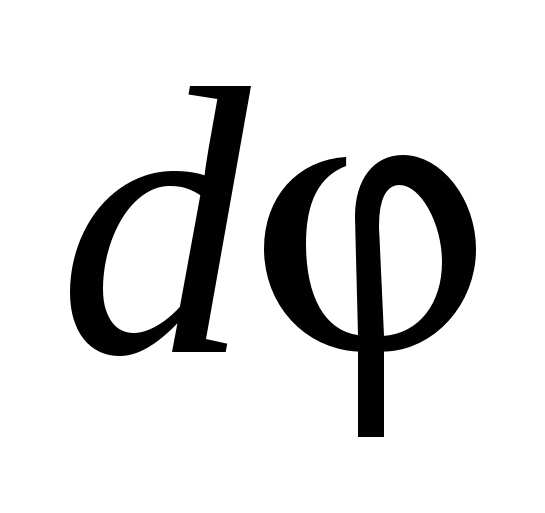 – угол поворота за время dt) – угол поворота за время dt)
|
1. вектор, направленный по касательной к траектории движения и равный 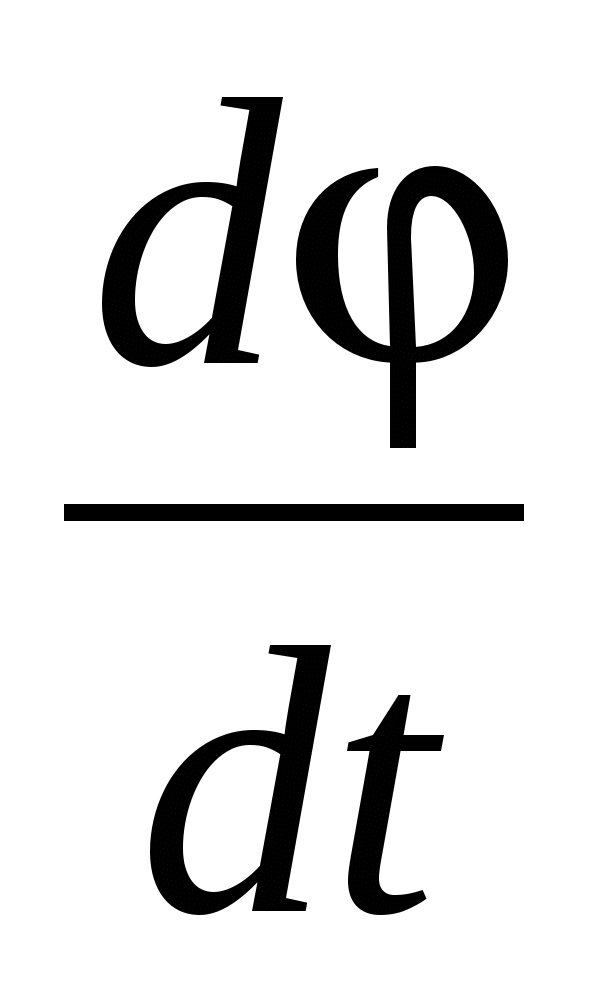 . .
2. псевдовектор, его направление определяется по правилу правого винта и равный 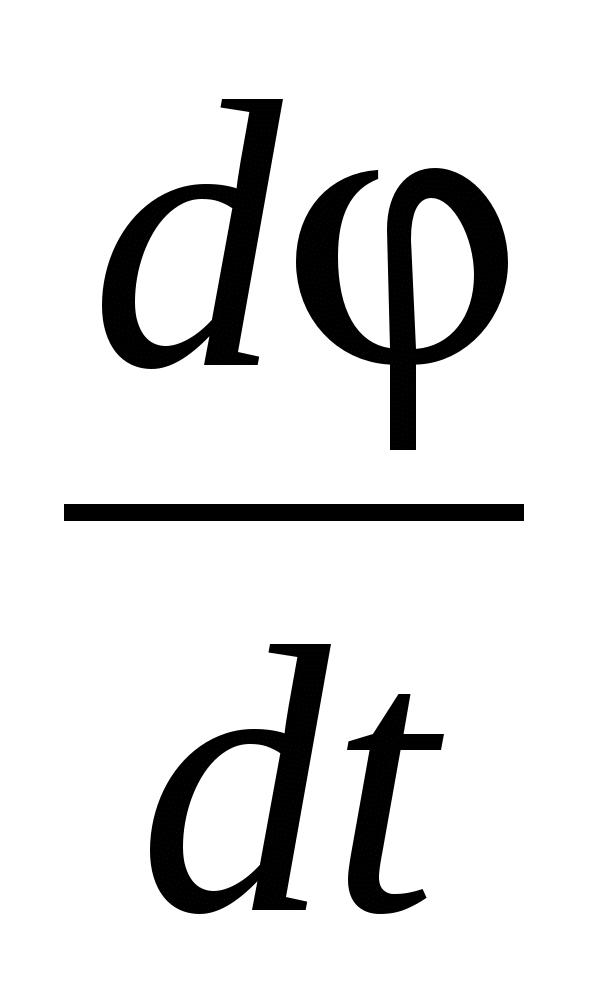 .! .!
3. скаляр равный 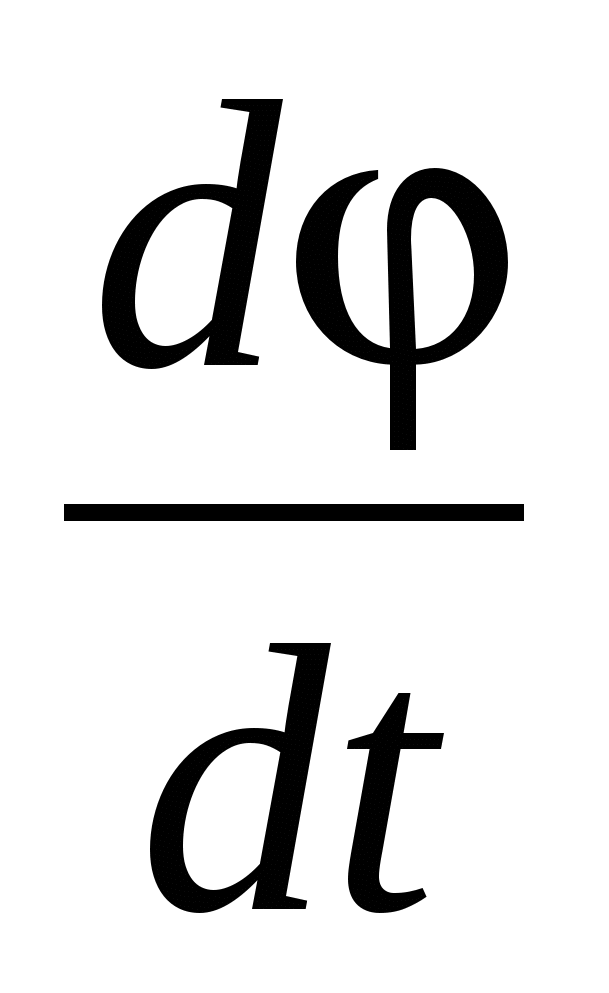 . .
4. псевдовектор, его направление определяется по правилу правого винта и равный 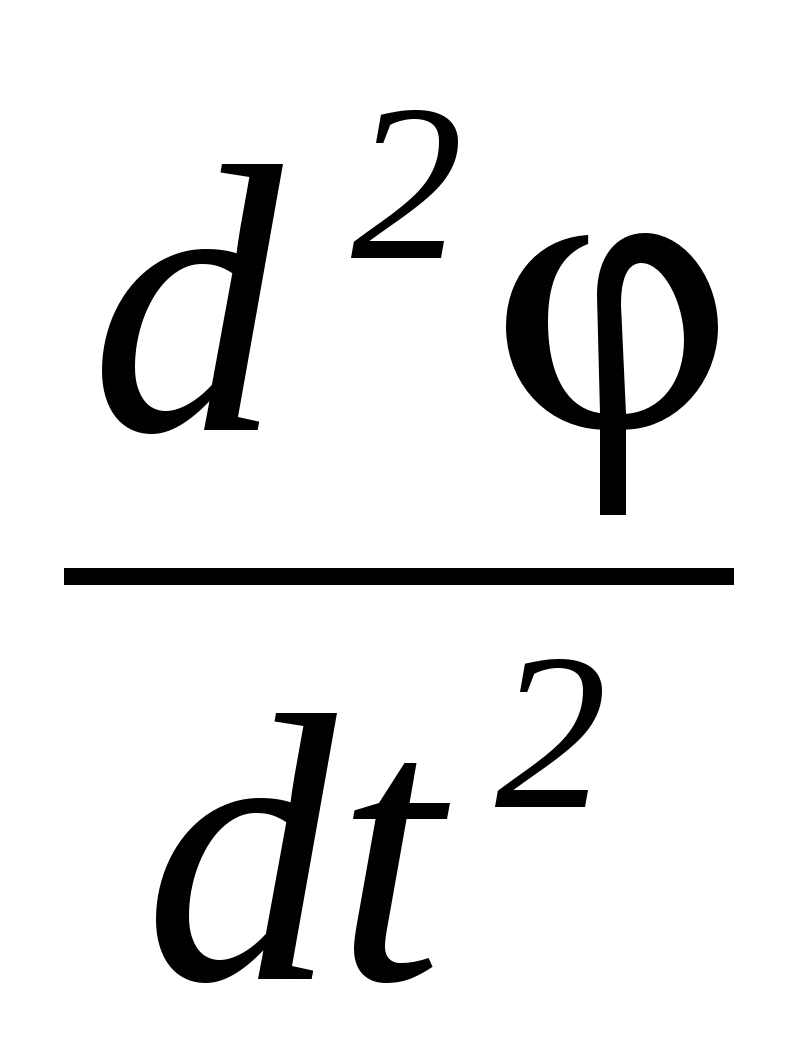 . .
|
 Скачать 1.71 Mb.
Скачать 1.71 Mb.