Метод. указания к ЛР № 47 (2020). Эффект холла в полупроводниках

• Название: Эффект холла в полупроводниках
• Дата: 16.04.2022
• Размер: 118.17 Kb.
• Имя файла: Метод. указания к ЛР № 47 (2020).docx
• Тип: Документы; #479167

КАСИМЕНКО Л.М. (2020)

Работа 47

ЭФФЕКТ ХОЛЛА В ПОЛУПРОВОДНИКАХ

Цель работы. Измерение холловской разности потенциалов в полупроводниковой пластине и определение концентрации, по- движности и знака носителей заряда, участвующих в токе.

Введение

Эффект Холла заключается в возникновении поперечной раз- ности потенциалов при пропускании тока через металлическую или полупроводниковую пластинку, помещенную в магнитное поле, направленное под некоторым углом к направлению тока.


j
Обычно вектор индукции магнитного поля Bнаправляют пер- пендикулярно вектору плотности тока ^→ .

Разность потенциалов возникает, как это показано на рис. 1, между точками Аи А₁,лежащими на прямой, перпендикулярной

_→ →

^{как к вектору} j ^{, так и к вектору индукции B . В отсутствие маг-} нитного поля точки А и А₁ лежат на эквипотенциальной поверхно- сти.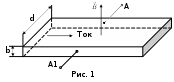





Классическая электронная теория объясняет эффект Холла следующим образом: поток электрических зарядов, попадая в магнитное поле, отклоняется от первоначального направления своего движения под действием силы Лоренца

где q– величина заряда,

F q[^→ B], (1)


d

d
^→ – средняя скорость направленного

движения носителей тока (дрейфовая скорость).

При этом одна из боковых сторон пластинки получает отрица- тельный заряд, в то время как противоположная сторона заряжа- ется равным ему по величине положительным зарядом. Накопле- ние зарядов происходит до тех пор, пока сила, действующая на электрический заряд со стороны холловского электрического по- ля, не уравновесит силу Лоренца:


d
qE q[^→ B]  0. (2)

Таким образом, напряженность поперечного холловского элек-

трического поля

E  [^→ B].

d

d
Если векторы ^→ и Bвзаимно перпендикулярны, то напряжен-

ность поперечного электрического поля равна по абсолютной ве-

личине E  B,   ^→ , что соответствует поперечной разно-

d d

сти потенциалов:

d
U_Х  Ed _dBd, (3)

где d– расстояние AA₁ (см. рис. 1).

Средняя скорость направленного движения носителей тока связана с плотностью тока j соотношением j  nq_d, где п – кон- центрация носителей заряда (число носителей в единице объема, q

– заряд носителя). Следовательно,

_d 

^j. (4)

nq

Выразив плотность тока через силу тока I:

j  ^I, (5)

bd

(b– толщина пластины) и подставив выражения (5) и (4) в (3), по- лучим

Х

Х
U ^IB  R^IB, (6)

qnb b

где

R_Х 
¹ . (7)

qn

Коэффициент R_Х называют постоянной Холла.

Формула (7) получается без учета закона распределения элек- тронов по скоростям. Более точный расчет с учетом закона рас- пределения носителей по скоростям в рамках классической стати- стики приводит к выражению для постоянной Холла


Х
R A¹ . (8)

qn

Для атомных полупроводников, например, для кремния,

A 3/8.

Для полупроводников с ионной связью, к которым относится рассматриваемое в данной работе интерметаллическое соедине- ние арсенид галлия, A 1. В этом случае применима формула (7).

Соотношение (6) позволяет определить постоянную Холла R_Х, м³/Кл, и концентрацию носителей заряда n, м^3 , в образце из опытных данных

_Ub IB

R_Х  ^X ; n

IB

U_X qb

. (9)

Если R_Х известно, то, измеряя U_Х и I, можно найти В. Этот спо- соб измерения Bиспользуется в технике (датчики Холла).

Важной характеристикой полупроводника является подвиж- ность в нем носителей заряда, под которой подразумевается сред- няя скорость, приобретаемая носителем в поле, напряженность которого равна единице. Если в поле напряженностью E носители приобретают скорость _d, то подвижность их u, м²/(Вс), равна

u  ^d . (10)

E

Используя связь между плотностью тока, напряженностью электрического поля и проводимостью j E и учитывая (4) и (10), можно выразить подвижность через проводимость  и кон- центрацию носителей заряда:

u ^ . (11)

nq

Из соотношений (7) и (11) следует

u R_Х. (12)

Таким образом, для определения подвижности носителей u

необходимо измерить R_Х и .

Знак постоянной Холла определяется знаком носителей заряда. У полупроводников постоянная Холла может быть отрицательной и положительной, так как существует два типа проводимости. У полупроводников с электронной проводимостью (полупроводни- ков n-типа) перемещаются электроны, и знак постоянной Холла отрицателен. У другого типа полупроводников электропровод- ность осуществляется положительными зарядами или так называ- емыми «дырками». Такие полупроводники называются дырочны- ми (полупроводниками р-типа). Они имеют положительный знак постоянной Холла. При этом q_n  q_p e.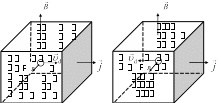


Зависимость знака постоянной Холла от знака носителей заря- да, создающих в данном веществе U_Х можно понять из рис. 2, на котором демонстрируется эффект Холла для образцов с положи- тельными и отрицательными носителями.
Рис. 2
Направление силы Лоренца F_Л изменяется на противополож- ное как при изменении направления движения зарядов, так и при изменении их знака. Следовательно, при одинаковом направлении тока и магнитной индукции B сила Лоренца, действующая на по- ложительные и отрицательные носители, имеет одинаковое направление. Поэтому в случае положительных носителей потен- циал передней грани (см. рис. 2) выше, чем задней, а в случае от- рицательных носителей – ниже. Таким образом, определив знак холловской разности потенциалов, можно установить знак носи- телей заряда, участвующих в токе.

Метод измерения и описание аппаратуры

Изучение эффекта Холла в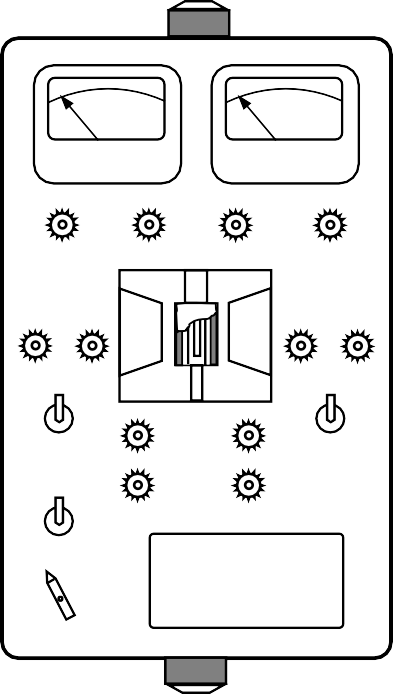

P₂
mA A


1 2 3 4

Э

N S

12 10 О Д 7 6
^П1 ^{9 5 П}2
11 8

П₃

Тб

Т

Р₁

Рис. 3

полупроводниках проводится на учебном приборе, общий вид и электрическая схема ко- торого представлены соответ- ственно на рис. 3 и 4. На рис. 4 участки схемы, собираемые с помощью добавочных прово- дов перед началом измерений, показаны штриховыми линия- ми. Исследуемый образец О (см. рис. 3), представляющий собой тонкий слой арсенида галлия, вмонтирован в про- зрачный диэлектрический дер- жатель Д, который можно пово- рачивать на 180° с помощью рукоятки P₁ в поле постоянного магнита.

Цилиндрический экран Э, изготовленный из ферромагне- тика, который можно переме- щать с помощью рукоятки Р₂

позволяет производить магнитную экранировку образца. Батарея гальванических элементов Б, (см. рис. 4) расположенная внутри прибора и включаемая тумблером Т, служит для создания про- дольного тока через образец. Величина тока регулируется потен- циометром П₃ и измеряется миллиамперметром, а его направле- ние изменяется с помощью переключателя П₁. Микроамперметр

А с симметричной относительно нуля шкалой, включаемый по- следовательно с сопротивлением R₁или R₂с помощью переклю- чателя П₂, служит для определения тока, вызванного разностью потенциалов Холла. Все приборы и приспособления закреплены на панели, в которую вмонтированы, также клеммы 1 – 12, с по- мощью которых осуществляется сборка цепи питания исследуе- мого образца и цепи измерения U_Х. В панели имеется окно для наблюдения за взаимным расположением магнитного экрана, ис- следуемого образца и постоянного магнита, южный и северный полюса которого обозначены буквами S и N. На лицевой части плиты расположена таблица Тб (см. рис. 3), в которой приводятся значения магнитной индукции поля постоянного магнита, удель- ной проводимости и толщины исследуемого образца, величины сопротивлений R₁ и R₂ и электрическая схема измерительной установки.

В данной работе исследуется поперечная (холловская) разность потенциалов в зависимости от величины протекающего по образ- цу продольного тока I при постоянном значении внешнего маг- нитного поля.

Для определения разности потенциалов Холла используют ме-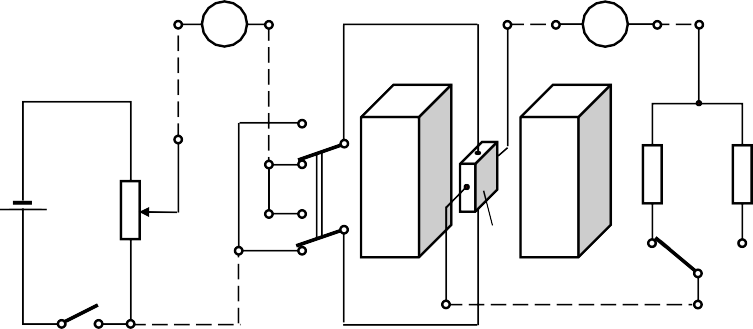

1 2 3 4

mA

_A 5 6

9

12

N S R₁ R₂

Б П₃ П₁

О

T 10

11 П₁

8 7

тод, основанный на измерении с помощью микроамперметра А, нагружаемого на два различных сопротивления R₁ и R₂ двух токов i₁ и i₂ в холловской цепи. Расчет U_Х производится по следующей формуле:


Х
_U i₁i₂ (R₁  R₂ ) _{. (13)}

i₂  i₁

Формула получается из решения уравнения Кирхгофа для хол- ловской цепи

U_Х  i(R R_К  R_i R_A), (14)

где R – нагрузочное сопротивление (R₁ или R₂); R_K – контактное сопротивление; R_i– сопротивление образца между холловскими электродами; R_A – сопротивление микроамперметра.

Подставляя вместо R значения R₁ и R₂, получим систему двух уравнений:

^U_X ^{ i1(R1  RK  Ri  RA )} _{. (15)}

^U i(R R R R )

_ X 2 2 K i A

Если выбирать значения токов i₁ и i₂ достаточно близкими друг другу, то контактное сопротивление R_K можно считать постоян- ным при измерениях. Решая систему уравнений (15), получим расчетную формулу (13).

Для исключения паразитных э.д.с., возникающих из-за наличия асимметрии холловских контактов и температурного градиента в образце, окончательное значение U_Х рассчитывается как среднее арифметическое из четырех измерений: двух при разном направ- лении продольного тока и двух – при разном направлении маг- нитного поля.

Порядок выполнения работы

1. 
   Собрать схему с помощью добавочных гибких проводов. При экранированном исследуемом образце О включить тумблер Т, установить потенциометром П₃ максимально возможное значе- ние продольного тока, показываемое миллиамперметром мА,и по
   

показаниям микроамперметра А убедиться в возможном нали- чии паразитных э.д.с. После этого продольный ток свести потен- циометром П₃ до минимально возможного значения, сдвинуть ру- кояткой Р₂ магнитный экран Э с исследуемого образца О и тем самым подготовить образец для измерения разности потенциалов Холла в поле постоянного магнита.

2. 
   Поставить переключатель ₁ в нижнее положение и устано- вить продольный ток величиной 2 мА. Микроамперметром изме- рить два значения тока в холловской цепи, включая с помощью переключателя П₂ сопротивления R₁ и R₂.
   
3. 
   Установить переключатель П₁ в верхнее положение и прове- сти измерения, указанные в п. 2.
   
4. 
   Рукояткой P₁ повернуть образец на 180°, изменив тем самым направление магнитного поля на противоположное, и провести измерения, указанные в пп. 2, 3.
   
5. 
   Весь процесс измерений, указанный в пп. 2  4, выполнить для значений продольного тока в 4, 6, 8 и 10 мА, т. е. для каждого значения продольного тока снимается 4 значения токов через об- разец. Полученные данные занести в таблицу. Выключить тум- блер Т и разобрать схему.
   

Таблица

№ п/п	I, мА	i1, мкА	i2, мкА	UХ i, B (i 1  4)	U 1 4 U , B Х 4  Хi i1
1
2
3
4

6. 
   Рассчитать значения разности потенциалов Холла по форму- ле (13), взяв значения сопротивлений R₁ и R₂ из таблицы на при- боре Тб; данные занести в таблицу.
   
7. 
   Оценить ошибку при расчете холловской разности потенци- алов для одного (любого) значения продольного тока:
   

U_X

U<sub>X

</sub> i₁

i<sub>1

</sub> i₂

i₂

2R



(R₁  R₂ )

2i

 ,

(i₂  i₁ )

где ∆i₁, ∆i₂, ∆i считать приборной ошибкой, а ∆R – точностью за- данных значений R.

8. 
   Построить график функции U_Х  f (I) и определить по нему среднее значение отношения U_Х/I.
   
9. 
   Вычислить значения постоянной Холла, концентрации носи- телей заряда по формуле (9), а подвижность – по формуле (12).
   
10. 
    Оценить погрешность в определении постоянной Холла, концентрации и подвижности носителей по соответствующим формулам:
    

R_X

R<sub>X

</sub> U_X

U<sub>X

</sub> bb

_ II

_ B_,

B

где ∆I– приборная ошибка, ∆bи ∆Bопределяются точностью за- данных значений b и B,

_n R_{X .}

n R<sub>X

u</sub> R_{X .}

u R_X

Контрольные вопросы

1. 
   В чем заключается эффект Холла?
   
2. 
   От чего зависит постоянная Холла R_Х?
   
3. 
   Что называется подвижностью электронов и дырок и как она зависит от температуры?
   
4. 
   Чему равна сила Лоренца и как определяется ее направление?
   
5. 
   Как определить знак носителей тока при помощи эффекта Холла?
   
6. 
   Укажите возможные области применения эффекта Холла.
   

Список литературы

1. 
   С а в е л ь е в И.В. Курс общей физики в 3-х тт. Т. 2. Элек- тричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.
   
2. 
   Физика твёрдого тела: Учебное пособие для технических университетов / И.К. Верещагин, С.М. Кокин, В.А. Никитенко, В.А. Селезнёв, Е.А. Серов; Под ред. И.К. Верещагина. – М.: Выс- шая школа, 2001. –237 с.
   
3. 
   А н д р е е в А.И., С е л е з н ё в В.А., Т и м о ф е е в Ю.П. Вводное занятие в лабораториях кафедры физики. – М.: РУТ (МИИТ), 2017. – 40 с.
   
4. 
   Н и к и т е н к о В.А., К о к и н С.М. Физика. Часть III. Развёрнутый конспект лекций. – М.: РУТ (МИИТ), 2019. – 213 с.