Практическая работа эконометрика. Эконометрика
 Скачать 493.77 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ ЭКОНОМЕТРИКА Группа Студент МОСКВА 2023 Практическая работа 1 Укажите основные этапы эконометрического исследования. Ответ: обычно выделяют следующие основные этапы эконометрического исследования: постановочный; априорный; этап параметризации; информационный; этапы идентификации; верификации модели. 1 этап (постановочный). На этом этапе формируется цель исследования, а также определяется набор экономических переменных, которые учувствуют в модели. Для выбора экономических переменных нужно теоретически обосновать каждую переменную. Объясняющие переменные не могут быть связаны функциональной или тесной корреляционной зависимостью, так как это может привести к невозможности оценки параметров модели или к получению неустойчивых, не имеющим реального смысла оценок. 2 этап (априорный). На этом этапе проводится анализ сущности изучаемого объекта, а также производится формирование и формализация априорной информации. 3 этап (параметризация). На этом этапе производится непосредственно моделирование, т.е. выбор вида модели, определяются входящие в нее связи. Основная задача, которая решается на данном этапе, – это выбор вида функции f(х) в эконометрической модели. Определяется возможность использования линейной модели, так как она наиболее проста и надежна. От того, насколько успешно решена проблема спецификации модели, в значительной степени зависит успех всего эконометрического моделирования. 4 этап (информационный). На данном этапе осуществляется сбор статистической информации – наблюдаемых значений экономических переменных. Здесь можно использовать наблюдения, которые получены как с участием исследователя, так и без его участия. 5 этап (идентификация модели). На данном этапе производится анализ модели и оценка ее параметров. С проблемой идентификации модели не следует путать проблему ее идентифицируемости, т.е. проблему возможности получения однозначно определенных параметров модели, заданной системой одновременных уравнений. 6 этап (верификация модели). На данном этапе проводится проверка истинности, адекватности модели. Выясняется, насколько удачно решены проблемы спецификации, идентификации и идентифицируемости модели, а также определяется точность расчетов по данной модели, в конечном счете, насколько соответствует построенная модель моделируемому реальному объекту или процессу. Следует также заметить, что если существуют статистические данные, которыми характеризуется моделируемый экономический объект в данный и предшествующие моменты времени, то для верификации модели, построенной для прогноза, достаточно сравнить реальные значения переменных в последующие моменты времени с соответствующими их значениями, полученными на основе рассматриваемой модели по данным предшествующих моментов. Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей. Ответ: Приведем некоторые виды аналитических зависимостей, наиболее часто используемых при построении моделей: 1) линейная  ;2) степенная  ;3) полулогарифмическая  ;4) гиперболическая  ;5) экспоненциальная  Могут применяться также комбинации рассмотренных зависимостей. Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии. Ответ: Парной регрессией называется уравнение связи двух переменных у и х вида y=f(x), где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор). Различают линейные и нелинейные регрессии. Линейная регрессия описывается уравнением:  .Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Примеры регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам: полиномы разных степеней  ;равносторонняя гипербола:  Примеры регрессий, нелинейных по оцениваемым параметрам: степенная  ;показательная  ;экспоненциальная  Наиболее часто применяются следующие модели регрессий: – прямой  ;– гиперболы  ;– параболы  ;– показательной функции  ;– степенная функция  Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции rxy. Ответ: Выборочный коэффициент корреляции является одним из основных показателей тесноты связи между двумя переменными. При изучении зависимости переменной Y от переменной Х выборочный коэффициент корреляции обозначается как rxy. При изучении зависимости переменной Х от переменной Y выборочный коэффициент корреляции обозначается как ryx. Выборочный парный коэффициент корреляции ryx:  ,где  – среднее арифметическое произведения факторной и результативной переменных:  – выборочное среднеквадратическое отклонение результативной переменной у , показывающее, на сколько единиц в среднем отклоняются значения результативной переменной у от ее среднего значения y: . – среднее значение из квадратов значений результативной переменной у: Объясните сущность метода анализа динамического ряда. Ответ: Ряды динамик представляют собой изменение показателей во времени. Рядом динамики (динамическим рядом, временным рядом) называется последовательность значений статистического показателя (признака), упорядоченная в хронологическом порядке, т.е. в порядке возрастания временного параметра. Отдельное наблюдение временного ряда называется уровнем этого ряда. Каждый ряд содержит значение времени и соответствующее значение уровней ряда. В зависимости от характера временного параметра ряды делятся на моментные и интервальные. В моментных – значение ряда приводятся на определенный момент времени, в интервальных – за определенный интервал времени. Уровни рядов динамики могут представлять собой абсолютные, относительные и средние величины. Если значения ряда представлены не непосредственно наблюдаемыми величинами, а рассчитанными относительными и средними величинами, их называют производными рядами динамики. Важной особенностью интервальных рядов динамики абсолютных величин является возможность суммирования их уровней. В результате этой процедуры получаются накопленные итоги. Суммирование уровней моментного ряда не производятся, так как они лишены логического смысла. Таким образом – моментные ряды динамики не обладают признаком адаптивности (добавлять). При анализе моментных рядов экономический смысл может иметь отклонение уровней ряда во времени. На практике часто требуется проанализировать динамику показателей не только за данный отрезок времени, но и с учетом ряда предшествующих периодов. Для этого строится ряд динамики с нарастающим итогом. Уровни такого ряда дают обобщающий результат развития показателя. Уровни ряда могут принимать детерминированные или случайные значения. Большое значение имеет величина интервала между соседними уровнями рядов. Удобно работать с равновеликими интервалами, ширина интервала не должна быть слишком большой, чтобы не упустить существенные закономерности в динамике показателя. Интервал не должен быть и слишком маленький, чтобы не загромождать ряд излишней детализацией и излишними вычислениями. Для правильного отражения временных рядов, необходимо обеспечить сопоставимость уровней ряда. Несопоставимость может определяться разной методикой расчета, разными условиями получения показателя, инфляцией, изменений границ области изучения показателей. Обычно, для обеспечения сопоставимости данных осуществляется пересчет или приведение данных к одному периоду цен, одним условиям, одной территории и т.п. При этом может теряться точность данных, что снижает ценность исходной информации, а, следовательно, затрудняет анализ. Задача: Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3 Таблица 3. Регрессионный анализ.
Решение: Линейная регрессия. Для расчета параметров a и b линейной регрессии, построим вспомогательную таблицу:
Система нормальных уравнений: 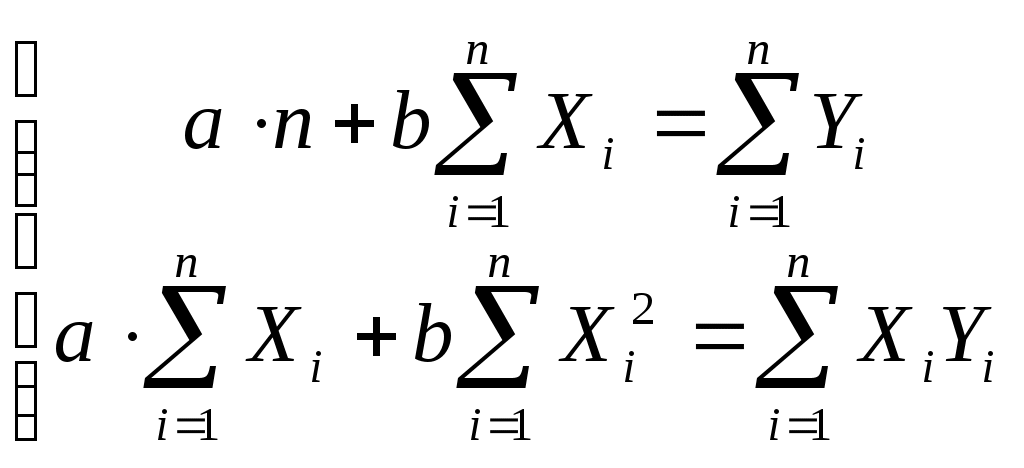 Тогда получим  , или  Сложив уравнения последней системы, получим:  Таким образом, получили:  .Уравнение линейной регрессии:  Экспоненциальная регрессия. Для расчета параметров регрессии построим расчетную таблицу:
Для наших данных система уравнений имеет вид:  или  Сложив уравнения последней системы, получим:  Таким образом, получили:  Уравнение экспоненциальной регрессии:  Степенная регрессия. Для расчета параметров регрессии построим расчетную таблицу:
Для наших данных система уравнений имеет вид  или  Сложив уравнения последней системы, получим:  Таким образом, получили:  Уравнение степенной регрессии:  Логарифмическая регрессия. Для расчета параметров регрессии построим расчетную таблицу:
Для наших данных система уравнений имеет вид  Решая данную систему уравнений, получили:  Уравнение логарифмической регрессии: Показательная регрессия. Для расчета параметров регрессии построим расчетную таблицу:
Для наших данных система уравнений имеет вид Решая данную систему уравнений, получили: Уравнение показательной регрессии:  Задача: Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4. Таблица 4. Корреляционный анализ.
Решение: Вычислим выборочные средние:    Вычислим выборочные дисперсии:  .  Вычислим среднее квадратическое отклонение:  .  Вычислим коэффициент корреляции:  Ответ:  |