Экспериментальное определение постоянной больцмана
 Скачать 53.38 Kb.
|
|
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ПОСТОЯННОЙ БОЛЬЦМАНА Цель работы: измерение парциального давления паров летучей жидкости; экспериментальное определение постоянной Больцмана. Приборы и принадлежности: стеклянный сосуд известного объема, водяной манометр с миллиметровой шкалой, соединительные шланги, шприц для впрыскивания жидкости, термометр, зажим. Основные теоретические сведения Опытным путем, еще до появления молекулярно-кинетической теории, был установлен целый ряд законов, описывающих поведение идеальных газов: законы Бойля-Мариотта, Шарля и Гей-Люссака. Эти законы описывают изотермический, изохорический и изобарический процессы, соответственно (см. предыдущую лаб. работу № 201 «Изучение газовых законов»). Французский физик и инженер Б. Клапейрон (17991864 гг.) вывел уравнение состояния идеального газа, объединив законы Бойля-Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V1, имеет давление p1 и находится при температуре Т1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами p2, V2, Т2 (см. рис. 202.1). Рассмотрим один из возможных переходов из состояния 1 в состояние 2 в виде процессов: 1) изотермического (изотерма 1–1/), 2) изохорического (изохора 1/2). 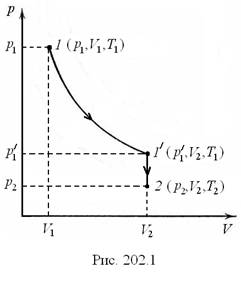 В соответствии с законами Бойля-Мариотта и Гей-Люссака, которые описывают эти процессы, запишем:  (202.1) (202.2)Исключив из уравнений (202.1) и (202.2)  , получим Так как состояния 1 и 2 были выбраны совершенно произвольно, то мы имеем возможность снять индексы 1, 2 и записать это в виде:  (202.3)Уравнение (202.3) является уравнением Клапейрона, в котором постоянная величина, стоящая справа, для каждого газа имеет свое значение, т.к. зависит от массы и химической природы газа. Русский ученый Д.И. Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (202.3) к одному молю, использовав молярный объем Vm. Согласно закону Авогадро при одинаковых р и Т моли всех газов занимают одинаковый молярный объем Vm, поэтому постоянная будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению  (202.4)называемому уравнением состояния идеального газа или уравнением Клапейрона-Менделеева, удовлетворяет лишь идеальный газ. Значение молярной газовой постоянной определим из формулы (202.4), учитывая, что моль газа находится при нормальных условиях: ро = 1,013105 Па, То = 273,15 К, Vm = 22,41103 м3/моль, тогда R = 8,31 Дж/(мольК). От уравнения (202.4) для одного моля газа можно перейти к уравнению Клапейрона-Менделеева для произвольной массы газа: если при некоторых заданных давлении и температуре один моль газа занимает молярный объем Vm, то при тех же условиях произвольное число молей газа займет объем  , где молярная масса (масса одного моля вещества). Единица молярной массы – килограмм на моль (кг/моль). Уравнение Клапейрона-Менделеева для произвольной массы m идеального газа имеет вид: (202.5)где  количество молей (количество вещества). В одном моле различных веществ содержится одинаковое число структурных единиц (атомов, молекул, ионов, электронов или любых других частиц), сколько содержится атомов в 12 г изотопа углерода  . Количество частиц в одном моле любого вещества постоянно и носит название числа Авогадро:  Постоянная Авогадро NA, молярная газовая постоянная R и постоянная Больцмана k связаны между собой соотношением:  Дж/K.Из уравнения (202.4) выразим давление и, используя, связь трех постоянных запишем:  где  концентрация молекул газа. Т. о., из уравнения (202.6)следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта:  м3.Описание рабочей установки и метода измерений Для выполнения работы используют установку, представленную на рис. 202.2. 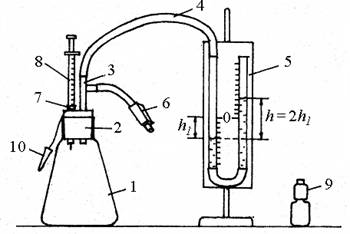 Рис. 202.2 Установка состоит из стеклянного сосуда 1, закрытого пробкой 2, в которую вставлена стеклянная трубка с тройником 3, на один из концов которого надет шланг 4, соединяющийся с водяным манометром 5. На другой конец тройника надета резиновая трубка, заканчивающаяся клапаном 6, перекрывающим сообщение сосуда с атмосферой. В пробку в отверстие 7 вставлен также шприц 8 для впрыскивания в сосуд летучей жидкости, хранящейся во флаконе 9. После впрыскивания жидкости в сосуд шприц сразу же вынимают и отверстие 7 быстро перекрывают пробкой 10. В этой работе для расчета постоянной Больцмана необходимо рассчитать парциальное давление паров летучей жидкости. Понятие парциального давления вводится при расчете давления смеси идеальных газов (см. закон Дальтона в работе «Изучение газовых законов»). Измерение парциального давления паров летучей жидкости производят следующим образом. В качестве летучей жидкости могут быть использованы ацетон (CH3COCH3), этанол (С2H5OH) или этиловый эфир (С2H5OC2H5). Молярные массы и плотности этих жидкостей приведены в таблице 202.1. Таблица 202.1
С помощью медицинского шприца из флакона набирают 0,05 0,1 мл жидкости. Затем шприц вместе с иглой вплотную вводят в отверстие 7 пробки стеклянного сосуда. С помощью зажима-клапана 6 обнуляют показания манометра, а затем этим же клапаном перекрывают сообщение сосуда с атмосферой. Зная объем Vж набранной жидкости и ее плотность, определяют массу жидкости  (202.7)где ж плотность используемой жидкости. Впрыснув жидкость в сосуд, вынув шприц и быстро перекрыв отверстие 7 пробкой 10, через 3 5 мин (когда разность уровней воды h в коленах манометра перестанет меняться), измеряют парциальное давление паров летучей жидкости  где в плотность воды. Для удобства измерения h начало миллиметровой шкалы манометра совмещают с первоначальным уровнем воды в коленах манометра (см. рис. 202.2). Тогда h = 2h1 и  (202.8)Теперь для того, чтобы определить постоянную Больцмана из уравнения (202.6), необходимо решить его относительно k:  (202.9) измерить с помощью термометра температуру и определить концентрацию молекул летучей жидкости в сосуде:  (202.10)где N число молекул летучей жидкости, которое можно найти следующим образом:  (202.11)здесь NA – число Авогадро, m – масса впрыскиваемой жидкости, а ее молярная масса. Объем V, доступный для движения молекул летучей жидкости,  (202.12)где V0 – объем сосуда с соединительными шлангами и левой трубки манометра до уровня воды, т.е. до нулевой отметки шкалы; S площадь сечения трубки водяного манометра; h1 – изменение уровня воды в левом или правом коленах манометра. С учетом формул (202.7, 202.8, 202.10 – 202.12), формулу (202.9) можно превратить в рабочую формулу:  Порядок выполнения работы и обработка результатов измерений 1.Открыть зажим 6, обеспечив сообщение сосуда 1 с атмосферой, и обнулить показания манометра 5. Закрыть зажим 6, перекрыв связь сосуда с атмосферой. 3.С помощью шприца набрать из флакона 0,05 или 0,1 мл (1 мл= 106 м3) летучей жидкости (это соответствует 2 или 4 делениям шкалы шприца, т.к. цена одного деления равна 0,025 мл). 4.Открыть отверстие 7 пробки сосуда и вставить туда шприц с набранной жидкостью. 5.Впрыснуть используемую жидкость с помощью шприца в сосуд и сразу же вынуть шприц, быстро закрыв отверстие 7 маленькой пробкой 10. 6.После этого дождаться момента, когда давление, измеряемое водяным манометром, перестанет увеличиваться (через 3 5 мин), занести в таблицу 2 изменение уровня воды h1 в коленах манометра. 7.Открыть зажим 6, выпустив в атмосферу пары летучей жидкости, обнулив тем самым показания манометра. Таблица 202.2
8.Параметры установки V0, S (спросите у преподавателя, ведущего занятия, или лаборанта), а также сведения об используемой жидкости (, ж, Vж) и температуру, измеренную комнатным термометром, занести в табл. 202.3. 9.По формуле (202.8) рассчитать парциальное давление паров летучей жидкости, полученный результат занести в табл. 202.2. 10.По формуле (202.13) рассчитать постоянную Больцмана k, результат занести с табл. 202.3. 11.Рассчитать абсолютную k и относительную Е погрешности измерений, исходя из табличного значения постоянной Больцмана:   Форма таблица 202.3
Вопросы для допуска к работе Какова цель работы? Дайте понятие идеального газа. Опишите рабочую установку и порядок выполнения работы. Запишите рабочую формулу и поясните входящие в нее величины. Вопросы для защиты работы 1.Сформулируйте законы, описывающие изотермический, изохорический, изобарический процессы. Приведите графики этих процессов. 2.Объединив законы Бойля-Мариотта и Гей-Люссака, получите объединенный газовый закон (закон Клапейрона). 3.Сформулируйте закон Авогадро. 4.Объединив уравнение Клапейрона с законом Авогадро, получите уравнение Клапейрона-Менделеева. 5.Сформулируйте закон Дальтона. Дайте определение парциального давления. 6.Используя постоянную Больцмана k, получите уравнение состояния идеального газа, выраженное через концентрацию молекул. 7.Что называется концентрацией молекул? 8.Выведите рабочую формулу (202.13). |