Контрольная. Задача Найти давление воздуха в резервуаре

• Название: Задача Найти давление воздуха в резервуаре
• Анкор: Контрольная
• Дата: 08.05.2021
• Размер: 1.07 Mb.
• Имя файла: 9e540ae.doc
• Тип: Задача; #202612
• страница: 1 из 2

Задача № 1.

Найти давление воздуха в резервуаре В (рис. 1), если избыточное давление на поверхности воды в резервуаре А равно р_и, разности уровней ртути ( = 13600 кг/м³) в двухколенном дифференциальном манометре h₁ и h₂, а мениск ртути в левой трубке манометра ниже уровня воды на h. Пространство между уровнями ртути в манометре заполнено спиртом ( = 800 кг/м³).



Рис. 1

Д ано: Решение:

р_и = 30 кПа; Так как давления в точках С и С^/ равны, то найдем давление в точке С,

h₁ = 190 мм; используя условие равновесия для плоскости 0-0:

h₂ = 230 мм; р_атм + р_и+ , где

h = 0,65 м; р_с = р_атм + р_и+ g = 98100 + 30000 + 9,81·(1000·0,65 - 13600·0,19) = 109128 Па = 109,128 кПа ;




Н айти: р_с = р_с^/ ;

р_в -? Рассмотрим правую часть двухколенного манометра:

р_с^/ + ρ_сп·g·h₁ = ρ_рт·g·h₂ + р_в → р_в = р_с^/ + g(ρ_сп·h₁ - ρ_рт· h₂) =

= + 9,81(800·0,19 - 13600·0,23) = 68917 Па = 68,9 кПа;

Очевидно, что в резервуаре вакуум.
Ответ: р_в = 68,9 кПа

Задача № 2.

Колокол 1 газгольдера диаметром D весит G (рис. 2). Определить разность уровней Н под колоколом газгольдера и в его станине 2.


Рис. 2

Д ано: Решение:

D = 6,1 м; Для обеспечения равновесия колокола, сила суммарного давления газа Р

G = 32,5 кН; на верхнее перекрытие колокола должна быть равна весу колокола G.

В то время сила суммарного давления на воду под колоколом:

Н айти: Р = р₀·S;

Н - ? где р₀- давление газа под колоколом; S – площадь колокола;

т.к. Р = G, то

м²;

Па;

Давление р₀, действующее на поверхности воды под колоколом, должно

быть уравновешенно разностью уровней воды Н.

Поэтому: р₀ = ρ_в·g·Н,

Откуда: м = 114 мм;

Ответ: Н = 0,114 м.

Задача № 3.

Щит, перекрывающий канал, расположен под углом к гориз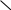онту и закреплен шарнирно к опоре над водой (рис. 3). Определить усилие, которое необходимо приложить к тросу для открытия щита, если ширина щита b, глубина воды перед щитом Н₁, а после щита Н₂. Шарнир расположен над высоким уровнем воды на расстоянии Н₃. Весом щита и трением в шарнире пренебречь.


l₃

l₂

l₁

Рис. 3

Д ано: Решение:

b = 1,85

H₁ = 2,3 м; Сила суммарного давления воды:

H₂ = 1,5 м; слева:

H₃ =1,03 м; Р₁ = р_с·S;

α = 60^о р_с = ρ·g· ; S = b· ;



Н айти: Р₁ = Н;

Т - ?

справа:

Р₂ = Н;

Находим расстояние от шарнира до центров приложения сил давления:

м;

3.27 м;
Составим уравнение моментов сил относительно шарнира О:
М₀ = -Р₁·l₁ + P₂·l₂ + T·l₃ =0;
где l₃ = (H₁ + H₃)·ctgα = (2.3 + 1,03)·ctg60^o = 1.92 м;
Тогда:

45.3 кН.
Ответ: Т = 45.3 кН.

Задача № 4.

Определить высоту вытяжной трубы вентиляционной системы, осуществляемой за счет разности веса теплового газа в сети и веса атмосферного воздуха. Газ вытесняется через трубу 1, а воздух притекает через зазоры крышки колодца 2 (рис. 4). Разность напоров 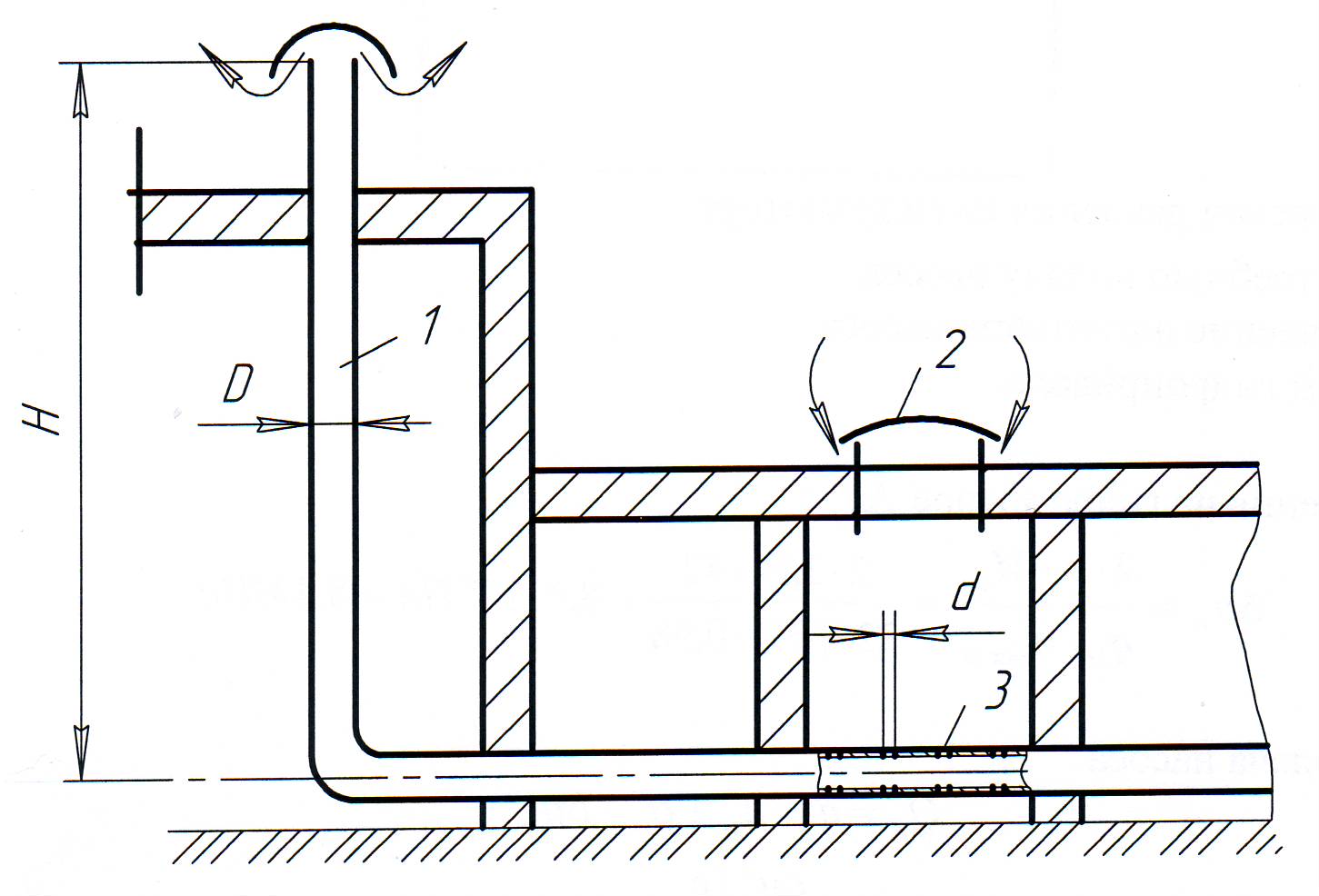. Определить количество и диаметр d приемных отверстий 3, если скорость газа в трубе , диаметр D. Температура газа в сети t₁, температура воздуха t₂.


Рис. 4




Дано: Решение:

Δh = 4,2 м.вод.ст.; 1.Определим плотности:

ω = 0,18 м/с; Т.к. в условии не сказано какой газ участвует в процессе,

D = 0,14 м; то принимаем за этот газ – воздух, только с более высокой

t₁ = 19,5 ^оС; температурой.

t₂ 11 ^оС; При t₁ = 19,5 ^оС; ρ₁ = 1,185 кг/м³;

При t₂ = 11 ^оС; ρ₂ = 1,23 кг/м³;

Найти:

H - ?

n - ?

d - ?



Разность напоров связана с разностью давлений формулой:

4.2·1000·9,81 = 41202 Па;

Разность давлений можно представить и как:

Δp = g·H·(ρ₂ – ρ₁);


Откуда:

93333.3 м;

2. Массовый расход в трубе:

0.0034 м³/с;
- массовый расход через одно приемное отверстие диаметра d;

Всего отверстий n, необходимо, чтобы V₂ = n·V₁;

Тогда:

;

Произвольно задаем количество отверстий: n = 15;

Тогда:

= 0,037 м ;
Ответ: Н = 93333.3 м; n = 15; d = 0.037 м = 37 мм.

Задача № 5.

Определить сжимающее усилие большого поршня F₂ и силу F₀, которую необходимо приложить к свободному концу рычага гидравлического пресса (рис. 5), если диаметр большого поршня D, длина рычага l, расстояние а. Усилие малого поршня F₁, диаметр малого поршня d.

О

Рис. 5

Д ано: Решение:

D = 92.5 мм; Напишем уравнение моментов сил относительно шарнирной точки О:

l = 550 мм; F₀·l = F₁·a;

a = 78 мм; откуда следует, что: кН;

F₁ =3.15 кН; в то же время ;

d = 20.5 мм; следовательно:

сжимающее усилие большого поршня:

Найти: кН;

F₀ – ?

F₂ - ? Ответ: F₀ = 0,447 кН; F₂ = 64,1 кН.



Задача № 6.

Определить величину и направление силы суммарного давления на секторный затвор, и ее направление (рис. 6). Глубина воды перед затвором Н, ширина затвора b.


B

C’


P



C

A

g2h_c

P_x

h_c




P_z


Рис. 6




Дано: Решение:

H
Р_z

Р
= 0,4 м;

b = 0,7 м;

α = 60^o




Н
Р_x
айти:

Р - ?

β - ? Определим горизонтальную составляющую силы Р:

Р_x = ρ·g·h_c·S_B;

h_c – глубина погружения центра тяжести вертикальной проекции;

h_c =

S_B – площадь вертикальной проекции смоченной поверхности;

S_B = b·H = 0,7·0,4 =0,28 м²;

Тогда : Р_x = 9,81·1000·0,2·0,28 = 549.36 Н;

Теперь определим вертикальную составляющую силы Р:

Р_z = γ·V; где V – тело давления (BCC^/В)

Так как тело давления не заполнено жидкостью, то Р_z ,будет направлена вверх

значит V = ;

R = м;

АС^/ = R·cosα = 0,46·cos60^o = 0,23 м;

S_ACC^/ = м²;

V_ACC^/ = b·S_ACC^/ = 0,7·0,046 =0.032 м²;

тогда объем тела давления:

V = 0.046 м³;

Поэтому Р_z = 9810·0,046 = 451.26 H;

Тогда величина искомой силы:

Н;
Определим угол, задающий направление силы Р:

tgβ =

β =39,4
Ответ: Р = 0,711 кН; β = 39,4.

Задача № 7.

Определить отрывающее и сдвигающее усилия и полную силу давления жидкости на полусферическую крышку радиуса R, если заданы пьезометрический напор воды Н над центром крышки и угол н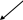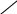аклона стенки бака к горизонту (рис. 7).


y




R_x

R_y

R

x

R_Fx

G_x




Рис. 7

Д ано: Решение:

H = 1,4 м; Используем уравнение равновесия жидкости, заполняющей

R = 0,4 м; полусферическую крышку. На объем жидкости, находящейся в

α = 60^o полусфере, действуют:

G_x – вес жидкости выделенного объема ( полусфера );

Найти: R_Fx – сила давления жидкости по плоскости круглого отверствия

Р_отр - ? радиусом R;

Р_сдв - ? R_х – сила реакций полусферической крышки;

R_Fx - ? проектируя эти силы на ось х, имеем:



∑х = R_Fx + G_x·cosα - R_х = 0;

следовательно:

R_х = R_Fx + G_x·cosα;

G_x = кН;

R_Fx = γ·Н·π·R² =10·1,4·3,14·0,4² = 7,03 кН;

где γ =10 кН/м³;

тогда:

Р_отр = R_х = 7,03 + 1,34·cos60^o = 7.7 кН;

проектируя силы на ось у, имеем:

∑у = G_x·sinα – R_y = 0;
P_сдв = R_y = 1.34·sin60^o = 1.16 кН;
Н;
Ответ: Р_отр = 7.7 кН; P_сдв = 1.16 кН; P = 7,79 кН.

Задача № 8.

Определить расход воды в трубопроводе диаметром d₁ при помощи водомера Вентури, если диаметр горловины d₂ и разность показаний пьезометров h (рис. 8).Температура воды t.


1

1

2

2

0

0

Ось трубы

Рис. 8
Д ано: Решение:

h = 470 мм; Составим уравнение Бернулли для сечений 1-1 и 2-2, принимая

t = 32 ^oC; за плоскость сравнения ось трубы:

d₁ = 320 мм;

d₂ = 160 мм; ;

Учитывая, что z₁ = z₂ = 0, пренебрегая в первом приближении

Найти: потерями напора, т.е. принимая = 0 и полагая α₁ = α₂ = 1;

V - ? получим:

;

Из уравнения неразрывности (постоянства расхода) течения имеем: V = S₁·υ₁ = S₂·υ₂;

т.к. , а , то ;

Обозначим: , тогда уравнение Бернулли запишется в виде:

;

Откуда:

;

Тогда расход воды в трубе:

;

Но так как мы пренебрегли потерями напора, то расход воды будет меньше. С учетом этих потерь формула для определения расхода запишется в виде:

μ· ;

где μ – коэффициент, учитывающий уменьшение расхода вследствие потерь напора.

Примем μ = 0,98

тогда:

0.0618 м³/с;

μ зависит от и числа Рейнольдса (по приложению 13 с.233 «Примеры расчетов по

гидравлике» под ред. Альтшуля, 1976 г.)

=0,5;

Re = ;

Скорость в сужении трубы: м/с;

Кинематическую вязкость воды находим по прил.2 для t = 32 ^оС, ν = 0,81·10^-6 м²/с;

Тогда Re = 607407.4 > 2320 (значит режим турбулентный)
Ответ: V = 0,0618 м³/с.


Задача № 9.

Сифонный бетонный водосброс внешним диаметром d общей длиной l сбрасывает воду из водохранилища в реку, уровень которой на Н ниже уровня водохранилища (рис. 9). Определить подачу сифонного водосброса, если он имеет два поворота: ₁ = 90⁰, ₂ с радиусами закругления R. Длина горизонтального участка l_г , толщина стенок водосброса δ. Температура воды в водохранилище t. Определить также вакуум в верхней точке сифона.


0

0

1

1

2

2


Рис. 9
Дано: d₁ = 0,6 м; H = 1,4 м; l = 45 м; l_г = 2,2 м; R = 2,3 м; α₂ = 40^o; δ = 30 мм; t = 20 ^oC; z₁ = 2,8 м; z₂ = 1,4 м;




Найти: V - ? P_вак - ?




Решение:

Разность уровней воды в водохранилище и реке определяет суммарные потери давления в сифонной трубе:

; где ;

Откуда скорость движения воды в сифоном водосбросе:

= ;

Примем первоначально, что водосброс работает в квадратичной области сопротивления, тогда по формуле 0,019;

где к_э = 0,5 мм ( бетонная труба, б.у. по справочнику );

коэффициент местного сопротивления на вход в трубу ( при δ/d = 0,03/0,6 = 0,05 )

ξ_вх = 0,5;

коэффициент сопротивления на поворот 90^о находим по формуле А.Д.Альтшуля:

= 0,189;

коэффициент сопротивления на поворот α₂ = 35^о определяется по формуле:

ξ₃₅^о = ξ₉₀^о·а = 0,189·0,65 = 0,123 где а = 0,65 ( по приложению для α₂ = 35^о );

коэффициент сопротивления на выход из трубы: ξ_вых = 1;

тогда сумма коэффициентов местных сопротивлений:

Σξ = ξ_вх + ξ₉₀^о + ξ₃₅^о + ξ_вых = 0,5+0,189+0,123+1 = 1,8;

Тогда: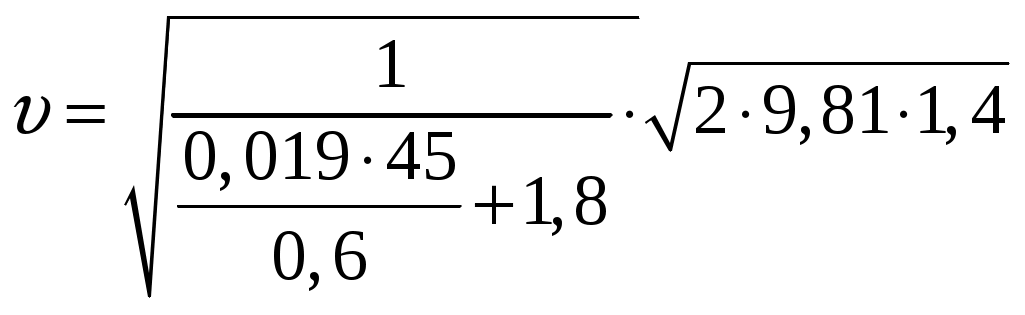

= 2,91 м/с;

определим Re ( при ν = 1,01·10^-6 м²/с для температуры воды t = 20 ^oC );

Re = ;

При =8,3·10^-4 ( по рис.3.4. ( с.61 ) установили, что выброс работает в квадратичной области сопротивления );

Расход воды через сифонный водосброс:

V = 0,82 м³/с;

Составим уравнение Бернулли для сечения 1-1 и 2-2:

;

Потери напора на учатке 1-2:

Δр_пот^1-2 = ;

где l₁= z₂ + l₂ = 1,4 + 2,2 =3,6 м;

ρ = 998 кг/м³ ( для воды при t = 20 ^oC );

Δр_пот^1-2 = 0,33·10⁴ Па;

Величина вакуума в верхней точке водосброса:

р_вак = р₁ – р₂ = 996·9,81·2,8+996· +0,33·10⁴ = 34748,2 Па;

Ответ: V = 0,82 м³/с; р_вак = 34,75 к Па.

Задача № 10.

По короткому трубопроводу, участки которого имеют диаметры d₁ и d₂, вода перетекает из закрытого бака с избыточным давлением воздуха р_м в открытый бак при постоянной разности уровней Н (рис. 10). Ось трубопровода заглублена под уровень в правом баке на h. Определить расход (пренебрегая потерями по длине) для случая, когда задвижка полностью открыта и ее коэффициент сопротивления ξ_з= 0, и для случая, когда она открыта на 0,25 и ξ_з.


2

2


0

0

1

1

Рис. 10
Д ано: Решение:
d₁ = 60 мм; выбираем сечение 1-1 и 2-2 и запишем уравнение Бернулли

d₂ =90 мм; относительно плоскости сравнения 0-0:

h = 2 м;

H = 3,9 м;

р_м = 190 кПа;

ξ_з = 16;




Найти:

V - ?




;

z₁ = h; z₂ = h + H;

р₂ = р_ат + ρ·g·( H + h );

p₁ = p_м + ρ·g·h;

жидкость вода, тогда предположим, что режим движения воды турбулентный, т.е.

α₁ = α₂ =1;

h_1-2 = h₁+h₂;

где h₁ – потеря напора в трубе с d₁; h₂ – потеря напора в трубе с d₂;

V = V₁ = V₂ – это условие выполняется для последовательного соединения участков

с разными диаметрами(уравнение постоянства расходов).



(1);

т.к. потери по длине не учитываются и про коэффициенты местных сопротивлений

ξ_вх и ξ_вых ничего в условии не сказано, то их примем ξ_вх = 0,5; ξ_вых = 1;

тогда: h₁ = ;

h₂ = ;

т.к. V₁ = S₁·υ₁;

V₂ = S₂·υ₂;

то: ; ;

h₁ + h₂ = (2);

подставим (2) в (1): (3);

из уравнения неразрывности течения имеем: ω₁·υ₁ = ω₂·υ₂;

т.к. , а , то (4);

подставим (4) в (3) и выражаем υ₁:

;

тогда:

;

;

Для ξ₃ = 0:

V₍₀₎ = = 0,01958 м³/с;

Ответ: V = 0,01958 м³/с.

Задача № 11.


По трубопроводу, состоящему из двух участков труб (см. Рис.) диаметрами и и длиной и подаётся бензин ( ) из бака с избыточным давлением в расположенный выше бак, где поддерживается вакуумметрическое давление . Разность уровней в баках . Коэффициент сопротивления трения для труб , коэффициенты местных сопротивлений ; ; . Требуется определить расход бензина .




Дано:

;

;

;

;

;



;

;

;

;

.

______________________






Решение:

Выбираем сечения 0 – 0 и 1 – 1, как показано на рисунке и записываем уравнение Бернулли, принимая за горизонтальную плоскость сравнения сечение 0 – 0:

, где



После подстановки получаем: .

В итоге для суммы потерь напора при движении бензина по трубопроводу получаем:

В то же время: .

При этом искомый нами расход бензина:

.

Из уравнения неразрывности течения имеем: .

Но так как: 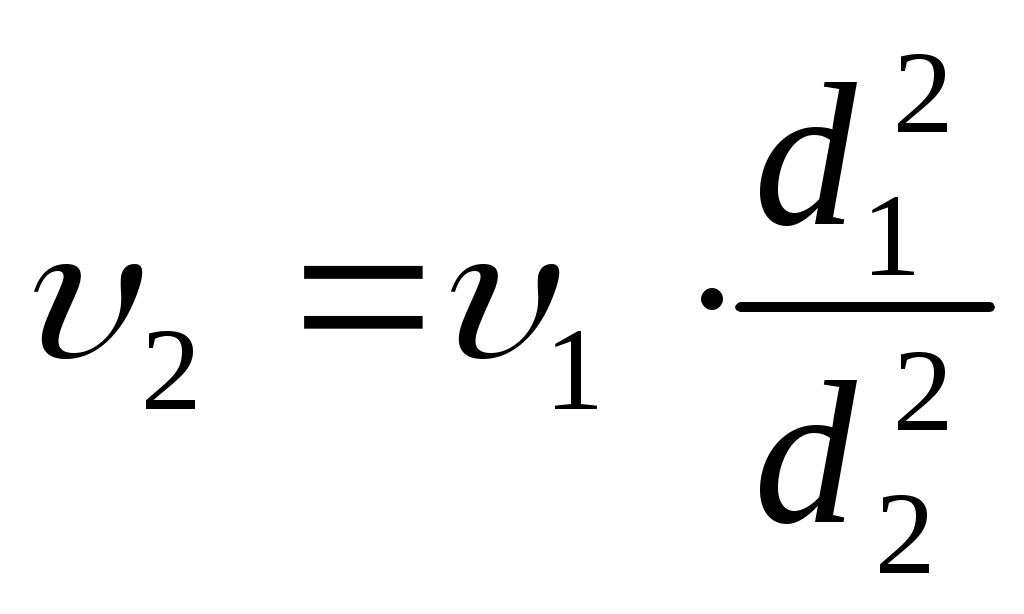и . Подставив это выражение в вышеуказанное получим:

Тогда следует:
Ответ:

Задача № 12.



Известны следующие величины простейшего гидравлического подъёмного устройства (см. Рис.): масса груза , длина стрелы , максимальный угол , давление нагнетания насоса , подача насоса

Требуется определить:

1. 
   Диаметр поршня гидроцилиндра ;
   
2. 
   Скорость движения штока при рабочем ходе ;
   
3. 
   КПД гидропривода при рабочем ходе, если КПД насоса .
   

Д ано:

;

;

;

;

;

.

__________________










Решение: