Билеты ЖБК Часть 1. Экзамен жбк сущность железобетона. Краткая историческая справка развития жбк
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
Для предельных состояний I группы: (расчет по несущей способности)
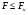 , ,где F– усилие от расчетных нагрузок (M, N или Q); Fu – предельное усилие, которое может выдержать элемент (минимальная несущая способность сечения элемента). Для предельных состояний II группы:
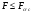 , ,где F– усилие от нормативных нагрузок (MилиN); Fcrc – внутреннее усилие, которое может выдержать элемент перед образованием трещин, т.е. при напряжениях в растянутой зоне сечения равных Rbtn.
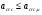 , ,где acrc– расчетное значение ширины раскрытия трещины; acrc,u – предельно допустимая ширина раскрытия трещины (приведена в СНиП 2.03.01-84* «Бетонные и железобетонные конструкции») .
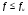 , ,где f– прогиб элемента от внешних воздействий; fu – предельный прогиб элемента, допустимый по условиям эксплуатации (приведен в СНиП 2.01.07-85* «Нагрузки и воздействия»).
7.1. Конструктивные требования к армированию элементов В целях обеспечения прочности при эксплуатации, транспортировании, хранении и монтаже, для восприятия неучитываемых расчетом различных усилий (усадочных, температурных), а также требуемой долговечности и совместной работы арматуры и бетона минимальный процент армирования μ рабочей продольной арматуры принимают равным:  ; ;  , ,где As,min – минимальная площадь сечения рабочей продольной арматуры; 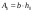 - площадь нормального сечения без учета свесов полки тавровых и двутавровых сечений. - площадь нормального сечения без учета свесов полки тавровых и двутавровых сечений.Минимальный процент армирования рабочей продольной арматуры в изгибаемых элементах 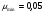 . Максимальное содержание рабочей продольной арматуры в нормльных сечениях элементов принимают не более 3%. . Максимальное содержание рабочей продольной арматуры в нормльных сечениях элементов принимают не более 3%. Конструктивные требования к минимальным расстояниям между стержнями арматуры приведены в СНиП 2.03.01-84* «Бетонные и железобетонные конструкции». 7.2. Конструирование плит Плита – плоская конструкция, толщина которой значительно меньше ширины и длины. Минимальная толщина плит: 40 мм – плиты покрытий; 50 мм – плиты перекрытий жилых и общественных зданий; 60 мм – плиты перекрытий промышленных зданий. Продольное армирование плиты – стержни укладываются параллельно направлению изгиба плиты. Плиты могут быть однопролетными и многопролетными (рис. 23), балочными и опертыми по контуру, сборными и монолитными. Плиты обычно армируют сварными сетками. Диаметр рабочих стержней сварных сеток не менее 3 мм, вязаных сеток не менее 6 мм. Расстояние между осями рабочих стержней S1 должно быть не более 200 мм, если высота плиты h менее 150 мм. При высоте плиты 150 мм и более S1 = 1,5h. Поперечные стержни располагают с шагом S2 = 250…300 мм (рис. 23, а), но не реже чем через 350 мм. Общее сечение поперечных стержней принимают не менее 10% сечения рабочей арматуры. Толщина защитного слоя для продольной рабочей арматуры в плитах принимается не менее 10…15 мм. 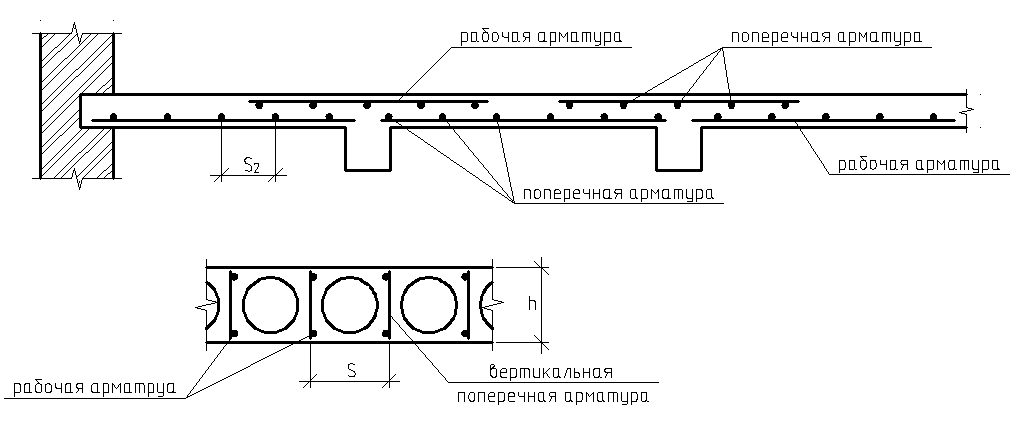 а) б)  ; но не более 200 мм. ; но не более 200 мм. Рис. 23. Армирование плит: а – многопролетная монолитная плита; б – однопролетная многопустотная плита. 7.3. Конструирование балок Балка – это линейная конструкция, размеры поперечного сечения которой существенно меньше длины. Конструктивные требования к размерам. Высота h кратно 50 мм, если h < 600 мм и кратно 100 мм, если h > 600 мм. Ширина 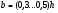 , а именно 100, 120, 150, 200, 220, 250 мм и далее кратно 50мм. , а именно 100, 120, 150, 200, 220, 250 мм и далее кратно 50мм. Железобетонные балки бывают прямоугольного, таврового, двутаврового, трапециевидного сечения (рис. 24). а) б) в) г) 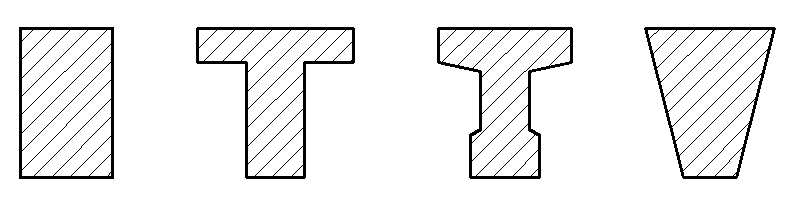 Рис. 24. Поперечное сечение балок: а – прямоугольное; б – тавровое; в – двутавровое; трапециевидное. 7.4. Расчет сечений изгибаемых балок по предельным состояниям I группы 7.4.1. Общий способ расчета прочности по нормальным сечениям Рассмотрим однопролетную железобетонную балку (рис. 25), свободно лежащую на двух опорах, симметрично загруженную двумя сосредоточенными силами. На определенной ступени загружения в балке образуются нормальные и наклонные трещины, в соответствии с этим прочность изгибаемых элементов рассчитывают как по нормальным, так и по наклонным сечениям. Прочность изгибаемых железобетонных конструкций рассчитывают по III стадии НДС. 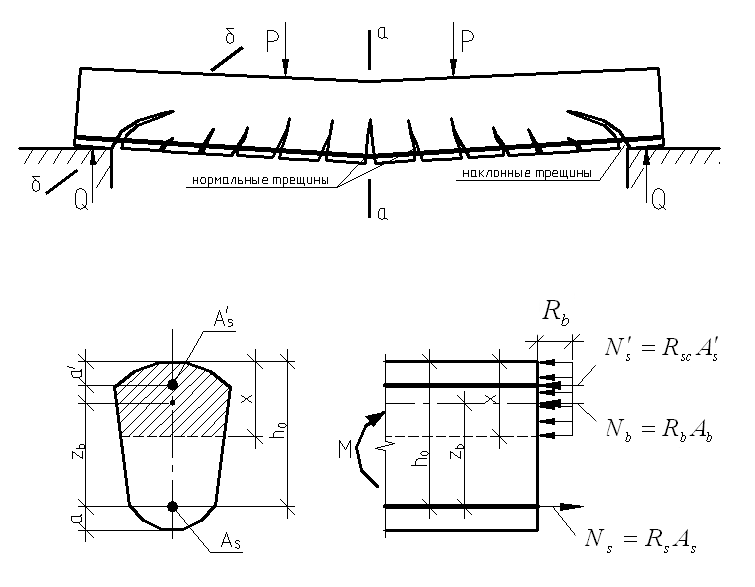 Рис. 26. Схема усилий при расчете прочности изгибаемых элементов по нормальному сечению. В расчетной схеме усилий (рис. 26) принимают, что на элемент действует изгибающий момент M, а в арматуре и бетоне действуют усилия, соответствующие напряжениям, равным расчетным сопротивлениям (при условии, что характер разрушения сечения соответствует 1 случаю III стадии НДС, когда в растянутой арматуре и сжатом бетоне достигнуты предельные сопротивления). В бетоне сжатой зоны сложную криволинейную эпюру напряжений заменяют прямоугольной, т.е. напряжение в бетоне Rb принимают одинаковым по всей высоте сжатой зоны. При этом принимают, что бетон растянутой зоны не работает σbt= 0. Сечение элемента может быть любой симметричной формы. В растянутой зоне имеется арматура площадью сечения Asс расчетным сопротивлением растяжению Rs, в сжатой зоне - арматура площадью сечения A’s с расчетным сопротивлением сжатию Rsc. Равнодействующие нормальных напряжений в арматуре и бетоне: 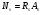 ; ; 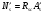 ; ; 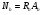 , где , где 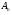 - площадь сечения бетона сжатой зоны. - площадь сечения бетона сжатой зоны.Из уравнения равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента можно определить площадь сечения бетона Abсжатой зоны, а по ней высоту сжатой зоны х. 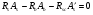 . .Общее условие прочности изгибаемых элементов по нормальным сечениям: момент внешних сил не должен превосходить момента внутренних усилий, т.е. прочность элемента достаточна, если внешний расчетный изгибающий момент не превосходит расчетной несущей способности сечения, выраженной в виде обратно направленного момента внутренних сил. 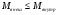 . .Условие прочности при моментах, взятых относительно оси, проходящей через точку приложения равнодействующей усилий в растянутой арматуре As: 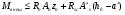 . .Высоту сжатой зоны х для сечений, характер разрушения которых соответствует 2 случаю III стадии НДС, когда разрушение происходит по сжатому бетону хрупко, а напряжения в растянутой арматуре предельного значения не достигают, также определяют из условия равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента, но в этом случае Rs заменяют напряжением 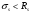 . . На основе экспериментов установлено, что напряжение 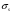 зависит от относительной высоты сжатой зоны бетона зависит от относительной высоты сжатой зоны бетона  . .Граничная относительная высота сжатой зоны бетона 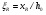 , при которой растягивающие напряжения в арматуре начинают достигать предельных значений , при которой растягивающие напряжения в арматуре начинают достигать предельных значений 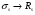 , зависит от класса бетона и класса арматуры и находится по формуле (25) СНиП 2.03.01-84* «Бетонные и железобетонные конструкции». , зависит от класса бетона и класса арматуры и находится по формуле (25) СНиП 2.03.01-84* «Бетонные и железобетонные конструкции».Таким образом, сечения, работающие по 1 случаю III стадии НДС, удовлетворяют условию: 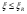 . .Сечения, не удовлетворяющие данному условию, соответствуют 2 случаю. Элементы прямоугольного профиля с одиночной арматурой (рис. 27). Высоту сжатой зоны х определяют из уравнения равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента:  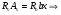  . .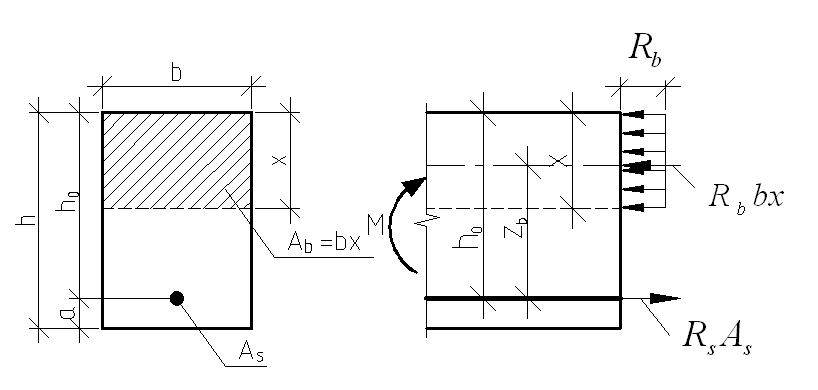 Рис. 27. Прямоугольное сечение с одиночной арматурой и схема усилий. Условие прочности по сжатой зоне: 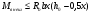 . (1) . (1)Условие прочности по растянутой арматуре: 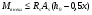 . (2) . (2)Данные формулы применяют при условии 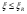 . .В практике для расчета прямоугольных сечений с одиночной арматурой используют табличный метод. С этой целью формулы (1) и (2) преобразуют следующим образом: 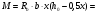 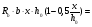 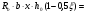 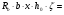 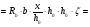 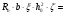 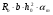 , ,где 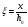 ; ; 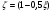 ; ; 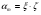 . . 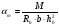 . (3) . (3) 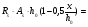 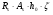 . . . (4) . (4)Для коэффициентов 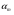 , , 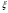 и и 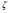 составлена таблица (приложение 1). По формуле (3) определяют составлена таблица (приложение 1). По формуле (3) определяют 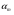 , затем по таблице в зависимости от , затем по таблице в зависимости от 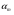 находят соответствующие находят соответствующие 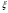 и и 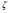 . Проверяют условие . Проверяют условие 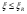 . Если условие выполняется, находят требуемое количество арматуры по формуле (4). . Если условие выполняется, находят требуемое количество арматуры по формуле (4).
Элементы прямоугольного профиля с двойной арматурой (рис. 28). Если при расчете прочности элемента прямоугольного профиля с одиночной арматурой оказалось, что 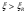 , значит прочности сжатой зоны бетона недостаточно и арматура в этой зоне требуется по расчету. , значит прочности сжатой зоны бетона недостаточно и арматура в этой зоне требуется по расчету. 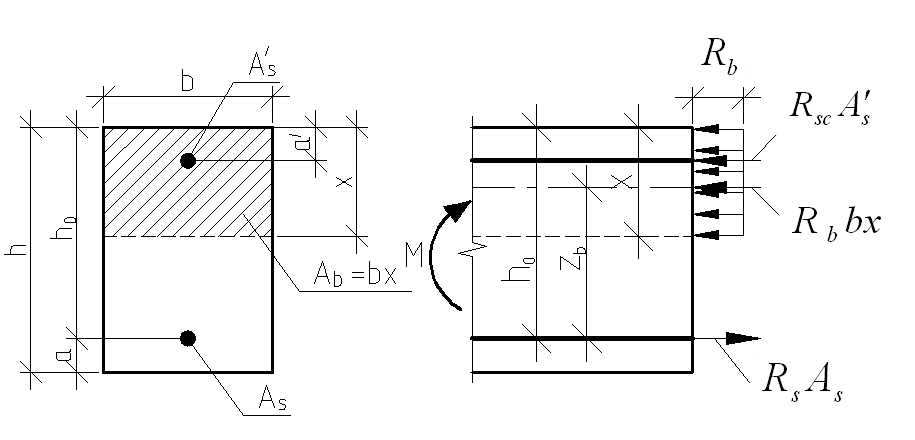 Рис. 28. Прямоугольное сечение с двойной арматурой и схема усилий. Условие прочности по сжатой зоне изгибаемого элемента, армированного двойной арматурой: 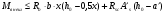 . (5) . (5)Из уравнения равенства нулю суммы проекций всех нормальных усилии на продольную ось элемента: 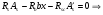  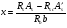 . .Если при расчете прочности элемента прямоугольного профиля с одиночной арматурой оказалось, что 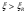 , принимают , принимают 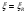 , затем по таблице находят соответствующее значение , затем по таблице находят соответствующее значение  . Формулу (5) преобразуем следующим образом: . Формулу (5) преобразуем следующим образом: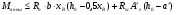 ; ;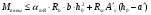 . (6) . (6)Требуемую площадь сжатой арматуры A’sможно определить из формулы (6): 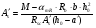 . .Из уравнения равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента находят требуемую площадь растянутой арматуры: 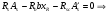   . .Элементы таврового профиля. Расчеты прочности некоторых железобетонных конструкций (многопустотные и ребристые плиты перекрытий) сводятся в итоге к расчету таврового сечения (рис. 29). Тавровое сечение образуется из полки и ребра. Основное преимущество таврового сечения перед прямоугольным – это отсутствие «лишнего» бетона в растянутой зоне, поэтому в сравнении с прямоугольным тавровое сечение значительно выгоднее, т.к. при одной и той же несущей способности (бетон растянутой зоны не влияет на несущую способность) расход бетона значительно меньше. При большой ширине полок участки свесов, более удаленные от ребра, напряжены меньше. Поэтому в расчеты вводят только часть полки, участвующей в работе – не более половины расстояния в свету между ребрами c и не более 1/6 пролета рассматриваемого элемента (рис. 30, а). При консольных свесах полок (рис. 30, б) вводимая в расчет ширина свеса должна составлять: - при 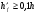 . . . . . . . . . . . . . . . . . . . . . не более 6 . . . . . . . . . . . . . . . . . . . . . не более 6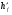 ; ;- при 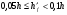 . . . . . . . . . . . . . . не более 3 . . . . . . . . . . . . . . не более 3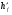 ; ;- при 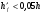 . . . . . . . . . . . . . . . . . . . свесы полок в расчете не учитывают. . . . . . . . . . . . . . . . . . . . свесы полок в расчете не учитывают. 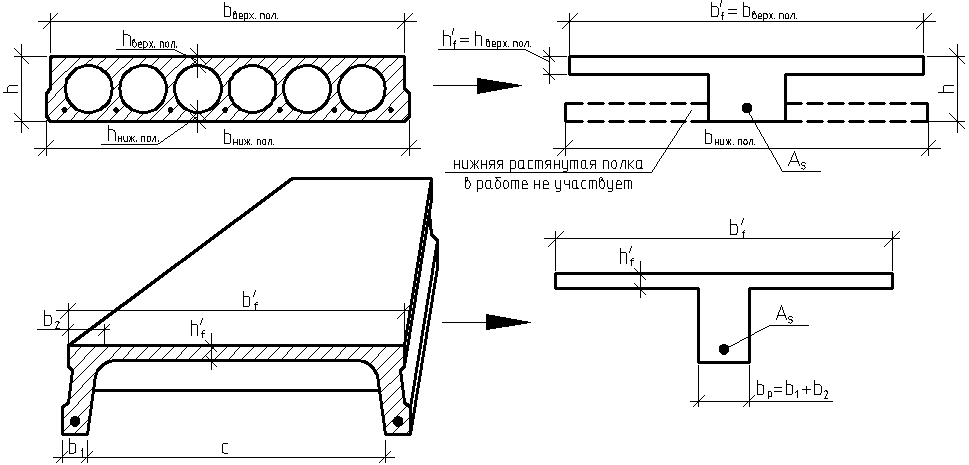 б) Рис. 29. Плиты перекрытий и их расчетные сечения: а – многопустотная плита; б – ребристая плита. 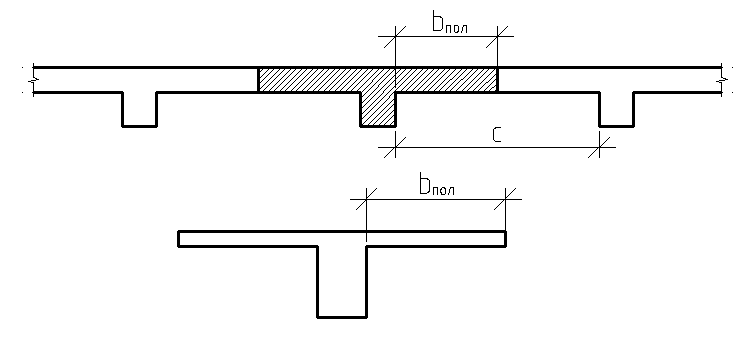 а) б) Рис. 30. Участки свесов тавровых сечений, вводимые в расчеты: а – в составе монолитного перекрытия; б – при консольных свесах полок. Два расчетных случая в элементах таврового профиля Расчетный случай зависит от положения границы сжатой зоны бетона. 1 случай. Граница сжатой зоны проходит в полке 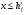 . В этом случае тавровое сечение рассчитывают как прямоугольное с размерами . В этом случае тавровое сечение рассчитывают как прямоугольное с размерами 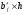 (рис. 31), поскольку бетон в растянутой зоне на несущую способность не влияет. (рис. 31), поскольку бетон в растянутой зоне на несущую способность не влияет.  Рис. 31. 1 случай положения границы сжатой зоны бетона в элементах таврового профиля. 2 случай. Граница сжатой зоны находится в ребре (рис. 32). Расчет проводят по формулам таврового профиля. Рис. 32. 2 случай положения границы сжатой зоны бетона в элементах таврового профиля. 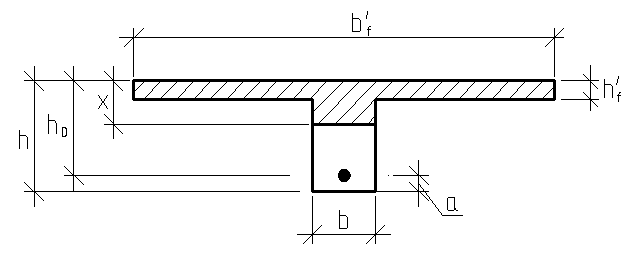 Определение расчетного случая При решении прямой задачи, т.е. когда необходимо определить требуемое количество растянутой арматуры, предполагают, что нижняя граница сжатой зоны проходит по нижней грани полки (рис. 33), определяют величину несущей способности таврового сечения на изгиб и сравнивают с величиной изгибающего момента от действия внешних нагрузок. 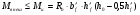 - граница сжатой зоны находится в полке; - граница сжатой зоны находится в полке;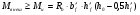 - граница сжатой зоны находится в ребре. - граница сжатой зоны находится в ребре. 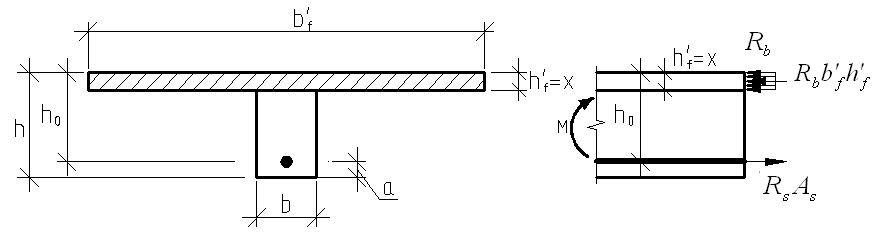 |
