экзаменационная работа. Структуры и алгоритмы обработки данных. Структуры и алгоритмы обработки данных. Экзамен по Структуры и алгоритмы обработки данных Работу
 Скачать 347.13 Kb. Скачать 347.13 Kb.
|
|
Экзамен по Структуры и алгоритмы обработки данных Работу выполнил: Рамиль Казань 2018 Вопрос 1. Рекурсивное добавление вершин в дерево поиска. Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями. 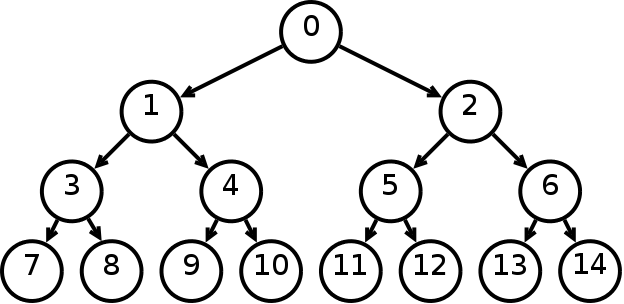 Рис. 1 Бинарное дерево Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается. 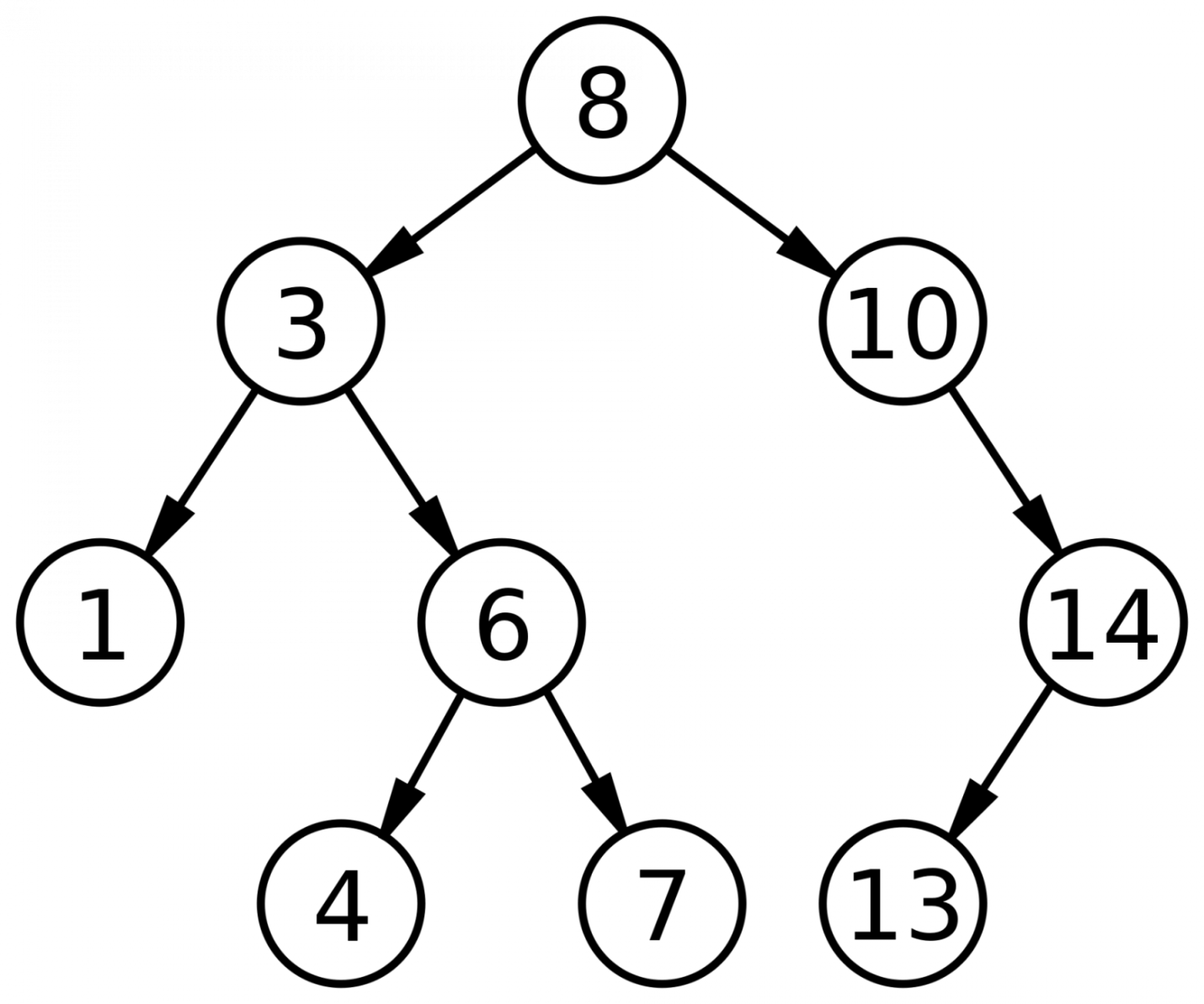 Рис. 2 Бинарное дерево поиска Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности. 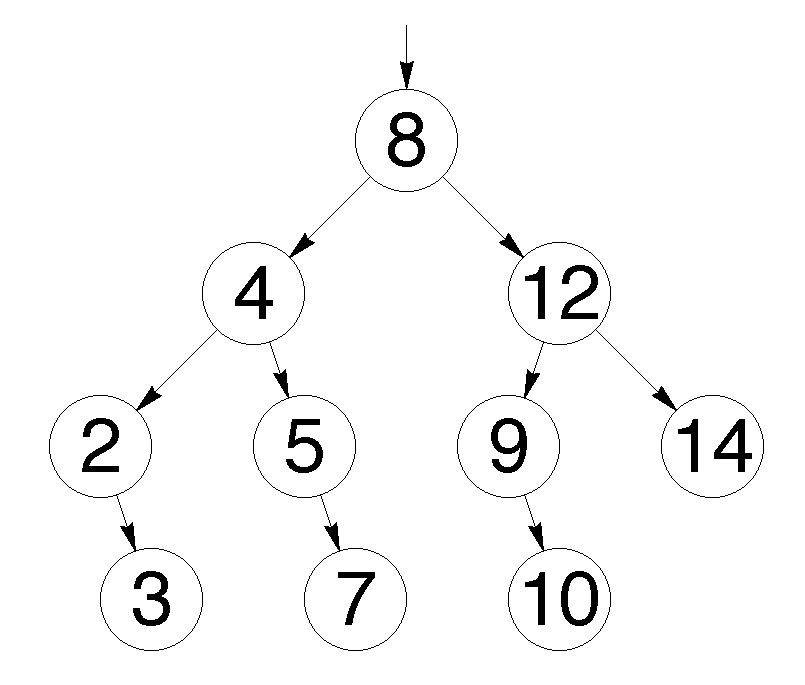 Рис. 3 Сбалансированное бинарное дерево поиска Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей. Например, в С++ ассоциативные контейнеры set и map представляют собой сбалансированное бинарное дерево поиска.  Рис. 4 Экстремально несбалансированное бинарное дерево поиска Теперь кратко обсудим рекурсию. Рекурсия в программировании – это вызов функцией самой себя с другими аргументами. В принципе, рекурсивная функция может вызывать сама себя и с теми же самыми аргументами, но в этом случае будет бесконечный цикл рекурсии, который закончится переполнением стека. Внутри любой рекурсивной функции должен быть базовый случай, при котором происходит выход из функции, а также вызов или вызовы самой себя с другими аргументами. Аргументы не просто должны быть другими, а должны приближать вызов функции к базовому случаю. Например, вызов внутри рекурсивной функции расчета факториала должен идти с меньшим по значению аргументом, а вызовы внутри рекурсивной функции обхода дерева должны идти с узлами, находящимися дальше от корня, ближе к листьям. Рекурсия может быть не только прямой (вызов непосредственно себя), но и косвенной. Например А вызывает Б, а Б вызывает А. С помощью рекурсии можно эмулировать итеративный цикл, а также работу структуры данных стек (LIFO). int factorial(int n) { if(n <= 1) // Базовый случай { return 1; } return n * factorial(n - 1); //рекурсивеый вызов с другим аргументом } // factorial(1): return 1 // factorial(2): return 2 * factorial(1) (return 2 * 1) // factorial(3): return 3 * factorial(2) (return 3 * 2 * 1) // factorial(4): return 4 * factorial(3) (return 4 * 3 * 2 * 1) // Вычисляет факториал числа n (n должно быть небольшим из-за типа int // возвращаемого значения. На практике можно сделать long long и вообще // заменить рекурсию циклом. Если важна скорость рассчетов и не жалко память, то // можно совсем избавиться от функции и использовать массив с предварительно // посчитанными факториалами). void reverseBinary(int n) { if (n == 0) // Базовый случай { return; } cout << n%2; reverseBinary(n/2); //рекурсивеый вызов с другим аргументом } // Печатает бинарное представление числа в обратном порядке void forvardBinary(int n) { if (n == 0) // Базовый случай { return; } forvardBinary(n/2); //рекурсивеый вызов с другим аргументом cout << n%2; } // Поменяли местами две последние инструкции // Печатает бинарное представление числа в прямом порядке // Функция является примером эмуляции стека void ReverseForvardBinary(int n) { if (n == 0) // Базовый случай { return; } cout << n%2; // печатает в обратном порядке ReverseForvardBinary(n/2); //рекурсивеый вызов с другим аргументом cout << n%2; // печатает в прямом порядке } // Функция печатает сначала бинарное представление в обратном порядке, // а затем в прямом порядке int product(int x, int y) { if (y == 0) // Базовый случай { return 0; } return (x + product(x, y-1)); //рекурсивеый вызов с другим аргументом } // Функция вычисляет произведение x * y ( складывает x y раз) // Функция абсурдна с точки зрения практики, // приведена для лучшего понимания рекурсии Кратко обсудим деревья с точки зрения теории графов. Граф – это множество вершин и ребер. Ребро – это связь между двумя вершинами. Количество возможных ребер в графе квадратично зависит от количества вершин (для понимания можно представить турнирную таблицу сыгранных матчей). Дерево – это связный граф без циклов. Связность означает, что из любой вершины в любую другую существует путь по ребрам. Отсутствие циклов означает, что данный путь – единственный. Обход графа – это систематическое посещение всех его вершин по одному разу каждой. Существует два вида обхода графа: 1) поиск в глубину; 2) поиск в ширину. Поиск в ширину (BFS) идет из начальной вершины, посещает сначала все вершины находящиеся на расстоянии одного ребра от начальной, потом посещает все вершины на расстоянии два ребра от начальной и так далее. Алгоритм поиска в ширину является по своей природе нерекурсивным (итеративным). Для его реализации применяется структура данных очередь (FIFO). Поиск в глубину (DFS) идет из начальной вершины, посещая еще не посещенные вершины без оглядки на удаленность от начальной вершины. Алгоритм поиска в глубину по своей природе является рекурсивным. Для эмуляции рекурсии в итеративном варианте алгоритма применяется структура данных стек. С формальной точки зрения можно сделать как рекурсивную, так и итеративную версию как поиска в ширину, так и поиска в глубину. Для обхода в ширину в обоих случаях необходима очередь. Рекурсия в рекурсивной реализации обхода в ширину всего лишь эмулирует цикл. Для обхода в глубину существует рекурсивная реализация без стека, рекурсивная реализация со стеком и итеративная реализация со стеком. Итеративная реализация обхода в глубину без стека невозможна. Асимптотическая сложность обхода и в ширину и в глубину O(V + E), где V – количество вершин, E – количество ребер. То есть является линейной по количеству вершин и ребер. Записи O(V + E) с содержательной точки зрения эквивалентна запись O(max(V,E)), но последняя не принята. То есть, сложность будет определятся максимальным из двух значений. Несмотря на то, что количество ребер квадратично зависит от количества вершин, мы не можем записать сложность как O(E), так как если граф сильно разреженный, то это будет ошибкой. DFS применяется в алгоритме нахождения компонентов сильной связности в ориентированном графе. BFS применяется для нахождения кратчайшего пути в графе, в алгоритмах рассылки сообщений по сети, в сборщиках мусора, в программе индексирования – пауке поискового движка. И DFS и BFS применяются в алгоритме поиска минимального покрывающего дерева, при проверке циклов в графе, для проверки двудольности. Обходу в ширину в графе соответствует обход по уровням бинарного дерева. При данном обходе идет посещение узлов по принципу сверху вниз и слева направо. Обходу в глубину в графе соответствуют три вида обходов бинарного дерева: прямой (pre-order), симметричный (in-order) и обратный (post-order). Прямой обход идет в следующем порядке: корень, левый потомок, правый потомок. Симметричный — левый потомок, корень, правый потомок. Обратный – левый потомок, правый потомок, корень. В коде рекурсивной функции соответствующего обхода сохраняется соответствующий порядок вызовов (порядок строк кода), где вместо корня идет вызов данной рекурсивной функции. Если нам дано изображение дерева, и нужно найти его обходы, то может помочь следующая техника (см. рис. 5). Обводим дерево огибающей замкнутой кривой (начинаем идти слева вниз и замыкаем справа вверх). Прямому обходу будет соответствовать порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами слева. Для симметричного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами снизу. Для обратного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами справа. В коде рекурсивного вызова прямого обхода идет: вызов, левый, правый. Симметричного – левый, вызов, правый. Обратного – левый правый, вызов. 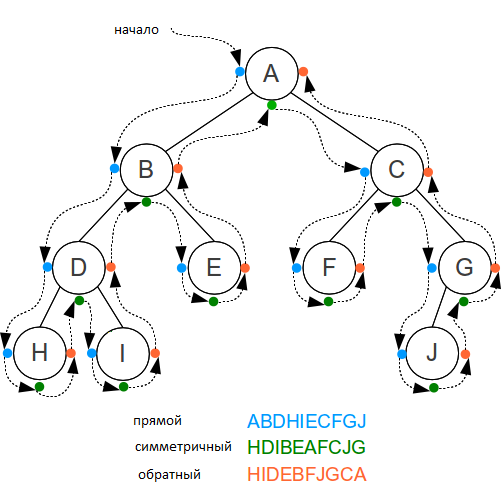 Рис. 5 Вспомогательный рисунок для обходов Для бинарных деревьев поиска симметричный обход проходит все узлы в отсортированном порядке. Если мы хотим посетить узлы в обратно отсортированном порядке, то в коде рекурсивной функции симметричного обхода следует поменять местами правого и левого потомка. struct TreeNode { double data; // ключ/данные TreeNode *left; // указатель на левого потомка TreeNode *right; // указатель на правого потомка }; void levelOrderPrint(TreeNode *root) { if (root == NULL) { return; } queue q.push(root); // Вставляем корень в очередь while (!q.empty() ) // пока очередь не пуста { TreeNode* temp = q.front(); // Берем первый элемент в очереди q.pop(); // Удаляем первый элемент в очереди cout << temp->data << " "; // Печатаем значение первого элемента в очереди if ( temp->left != NULL ) q.push(temp->left); // Вставляем в очередь левого потомка if ( temp->right != NULL ) q.push(temp->right); // Вставляем в очередь правого потомка } } void preorderPrint(TreeNode *root) { if (root == NULL) // Базовый случай { return; } cout << root->data << " "; preorderPrint(root->left); //рекурсивный вызов левого поддерева preorderPrint(root->right); //рекурсивный вызов правого поддерева } // Функция печатает значения бинарного дерева поиска в прямом порядке. // Вместо печати первой инструкцией функции может быть любое действие // с данным узлом void inorderPrint(TreeNode *root) { if (root == NULL) // Базовый случай { return; } preorderPrint(root->left); //рекурсивный вызов левого поддерева cout << root->data << " "; preorderPrint(root->right); //рекурсивный вызов правого поддерева } // Функция печатает значения бинарного дерева поиска в симметричном порядке. // То есть в отсортированном порядке void postorderPrint(TreeNode *root) { if (root == NULL) // Базовый случай { return; } preorderPrint(root->left); //рекурсивный вызов левого поддерева preorderPrint(root->right); //рекурсивный вызов правого поддерева cout << root->data << " "; } // Функция печатает значения бинарного дерева поиска в обратном порядке. // Не путайте обратный и обратноотсортированный (обратный симметричный). void reverseInorderPrint(TreeNode *root) { if (root == NULL) // Базовый случай { return; } preorderPrint(root->right); //рекурсивный вызов правого поддерева cout << root->data << " "; preorderPrint(root->left); //рекурсивный вызов левого поддерева } // Функция печатает значения бинарного дерева поиска в обратном симметричном порядке. // То есть в обратном отсортированном порядке void iterativePreorder(TreeNode *root) { if (root == NULL) { return; } stack s.push(root); // Вставляем корень в стек /* Извлекаем из стека один за другим все элементы. Для каждого извлеченного делаем следующее 1) печатаем его 2) вставляем в стек правого! потомка (Внимание! стек поменяет порядок выполнения на противоположный!) 3) вставляем в стек левого! потомка */ while (s.empty() == false) { // Извлекаем вершину стека и печатаем TreeNode *temp = s.top(); s.pop(); cout << temp->data << " "; if (temp->right) s.push(temp->right); // Вставляем в стек правого потомка if (temp->left) s.push(temp->left); // Вставляем в стек левого потомка } } // В симметричном и обратном итеративном обходах просто меняем инструкции // местами по аналогии с рекурсивными функциями. Вопрос 2. Поразрядная сортировка массивов. Поразрядная сортировка была изобретена в 1920-х годах как побочный результат использования сортирующих машин. Такая машина обрабатывала перфокарты, имевшие по 80 колонок. Каждая колонка представляла отдельный символ. В колонке было 12 позиций, и в них для представления того или иного символа пробивались отверстия. Цифру от 0 до 9 кодировали одним отверстием в соответствующей позиции (еще две позиции в колонке использовали для кодировки букв). Запуская машину, оператор закладывал в ее приемное устройство стопку перфокарт и задавал номер колонки на перфокартах. Машина "просматривала" эту колонку на картах и по цифровому значению 0, 1, ..., 9 в ней распределяла ("сортировала") карты на 10 стопок. Несколько колонок (разрядов) с закодированными цифрами представляли натуральное число, т.е. номер. Чтобы получить стопку карт, упорядоченных по номерам, оператор действовал так. Вначале он распределял карты на 10 стопок по значению младшем разряде. Эти стопки в порядке возрастания значений в младшем разряде он складывал в одну и повторял процесс, но со следующим разрядом, и т.д. Получив стопки карт, распределенных по значениям в старшем разряде, оператор складывал их по возрастанию этих значений и получал то, что нужно. Значения в разрядах номеров заданы цифрами, поэтому поразрядную сортировку еще называют цифровой. Заметим, что цифры от 0 до 9 упорядочены по возрастанию, поэтому цифровая сортировка располагает числа в лексикографическом порядке. Пример. Входные данные 733 877 323 231 777 721 123 Выходные данные 123 231 323 721 733 777 877 Описание решения. Принцип решения разберем на конкретном примере. Пусть задана последовательность трехзначных номеров: 733 877 323 231 777 721 123 Распределим данную последовательность по младшей цифре на стопки: 231 721 733 323 123 877 777 Далее сложим получившиеся стопки в одну в порядке возрастания последней цифры. 231 721 733 323 123 877 777 На следующем шаге номера, которые обрабатываются именно в этой последовательности, распределяются по второй цифре на следующие стопки. 721 323 123 231 733 877 777 Затем из них также образуется одна последовательность. 721 323 123 231 733 877 777 Обратим внимание, что перед последним шагом все номера с числом сотен 7, благодаря предыдущим шагам, расположены один относительно другого по возрастанию. На последнем шаге номера распределяются по старшей цифре на стопки: 123 231 323 721 733 777 877 и образуется окончательная последовательность: 123 231 323 721 733 777 877. #include "stdafx.h" #include using namespace std; const int D = 3; const int B = 10; typedef int T[D]; typedef T *List; void SortD(int k); void Done(); void outDigs(int i); List Data; int PFirst[B], PLast[B], *PQNext; int first, n, newL, tempL, i, nextI; int _tmain(int argc, _TCHAR* argv[]){ int k; cout << "Введите количество элементов массива n "; cin >> n; Data = new T[n]; PQNext = new int[n]; for ( k = 0 ; k < n ; k++ ){ PQNext[k] = k + 1; for ( int r = 0 ; r < D ; r++ ) Data[k][r] = 0; } for ( k = 0 ; k < n ; k++ ) for ( int r = 0 ; r < D ; r++ ) Data[k][r] = rand()%B; first = 0; Done(); cout << endl; for ( k = D - 1 ; k >= 0 ; k-- ) SortD(k); Done(); cout << endl; delete [] PQNext; delete [] Data; system("pause"); return 0; } // описание функции поразрядной сортировки void SortD(int k){ for ( tempL = 0 ; tempL < B ; tempL++ ){ PFirst[tempL] = n; PLast[tempL] = n; } i = first; while (i != n){ tempL = Data[i][k]; nextI = PQNext[i]; PQNext[i] = n; if ( PFirst[tempL] == n ) PFirst[tempL] = i; else PQNext[PLast[tempL]] = i; PLast[tempL] = i; i = nextI; } tempL = 0; while ( tempL < B && PFirst[tempL] == n ) tempL++; first = PFirst[tempL]; while ( tempL < B - 1 ){ newL = tempL + 1; while ( newL < B && PFirst[newL] == n ) newL++; if ( newL < B ) PQNext[PLast[tempL]] = PFirst[newL]; tempL = newL; } } /*описание функции вывода элементов в соответсвии со списком индесов в массиве PQNext*/ void Done(){ int i = first; while ( i != n ){ outDigs(i); i = PQNext[i]; } } /*описание функции вывода элементов из массива Data, индекс которого задан ее аргументом*/ void outDigs(int i){ int j = 0; while ( Data[i][j] == 0 && j < D ) j++; if ( j == D ) cout << 0; else while ( j < D ) cout << Data[i][j++]; cout << " "; } Вопрос 3. Задание: Описать структуру Список (статическая реализация). Представить фрагмент программного кода – Поиск и Удаление элемента Статическая реализации списка на основе массива использует принцип указателей (но БЕЗ динамического распределения памяти). В этом случае каждый элемент списка (кроме последнего) должен содержать номер ячейки массива, в которой находится следующий за ним элемент. Это позволяет РАЗЛИЧАТЬ физический и логический порядок следования элементов в списке. Удобно (но НЕ обязательно) в начале массива ввести фиктивный элемент-заголовок, который всегда занимает нулевую ячейку массива, никогда не удаляется и указывает индекс первого реального элемента списка. В этом случае последний элемент списка (где бы он в массиве не располагался) должен в связующей части иметь некоторое специальное значение-признак, например – индекс 0. Схема физического размещения элементов списка в массиве:
Соответствующая схема логического следования элементов списка:
Тогда необходимые объявления могут быть следующими: Const N = 100; TypeTListItem = record Inf : <описание>; Next : integer; end; Var StatList : array [0 . . N] of TListItem; Рассмотрим реализацию основных списковых операций. Условие пустоты списка: StatList [ 0 ].Next = 0; Проход по списку: · ввести вспомогательную переменную Current для отслеживания текущего элемента списка и установить Current := StatList [ 0 ].Next; · организовать цикл по условию Current = 0, внутри которого обработать текущий элемент StatList [ Current ].Inf и изменить указатель Current на следующий элемент: Current := StatList [ Current ].Next Поиск элемента аналогичен проходу, но может заканчиваться до достижения конца списка: Current := StatList [ 0 ].Next; While (Current <> 0) and (StatList [ Current ].Inf <> ‘значение’ do Current := StatList [ Current ].Next; If Current = 0 then ‘поиск неудачен’ else ‘элемент найден’; Удаление заданного элемента (естественно, в случае его наличия в списке) также требует изменения связующей части у элемента-предшественника. Это изменение позволяет “обойти” удаляемый элемент и тем самым исключить его из списка. Необходимые шаги: · определение каким-то образом удаляемого элемента (например – запрос у пользователя) · поиск удаляемого элемента в списке с одновременным отслеживанием элемента-предшественника; пусть индекс удаляемого элемента есть i, а индекс его предшественника - s · изменение связующей части элемента-предшественника с индекса i на индекс-значение связующей части удаляемого элемента i: StatList [s].next := StatList [ i ].next; · обработка удаляемого элемента (например – вывод информационной части) · включение удаленного элемента во вспомогательный список без его уничтожения или освобождение ячейки i с включением ее в список свободных ячеек (методы поддержки свободной памяти рассматриваются ниже)
Реализация списков на основе массивов с указателями-индексами требует постоянного отслеживания свободных и занятых ячеек массива. Можно предложить два подхода. Первый - более простой, но менее эффективный: все свободные ячейки в связующей части содержат какой-либо специальный номер, например – число ( -1). Тогда при начальном создании пустого списка во все ячейки (кроме нулевой с заголовком) в связующие части помещается значение ( -1). Если при удалении элемента из списка соответствующая ячейка должна стать свободной, то в ее связующую часть записывается значение ( -1), что возвращает эту ячейку в набор свободных. При добавлении нового элемента поиск свободной ячейки организуется просмотром всего массива до обнаружения первой ячейки со значением ( -1). Именно эта операция в некоторых случаях может приводить к росту вычислительных затрат, если случайно все свободные ячейки оказались в конце массива, а сам массив является достаточно большим (например, содержит сотни тысяч ячеек). Второй - более эффективный, но и более сложный способ состоит в том, что все свободные ячейки связываются во вспомогательный список, из которого они берутся при добавлении нового элемента в основной список, и куда они возвращаются при удалении элементов из основного списка. При этом вспомогательный список может иметь самое простейшее поведение – например стековое: последняя освободившаяся ячейка массива будет использована для размещения нового элемента в первую очередь. Какие дополнительные действия необходимы для реализации данного способа? Прежде всего, при создании пустого списка все ячейки массива (кроме нулевой) связываются во вспомогательный список свободных ячеек: for i := 1 to N-1 do StatList [ i ]. Next := i + 1; StatList [ N ]. Next := 0; Начало вспомогательного списка задается переменной StartFree с начальным значением 1. Удаление элемента из основного списка приводит к изменению связующей части удаленного элемента и изменению значения переменной StartFree на индекс удаленного элемента. При добавлении нового элемента свободная ячейка определяется по значению переменной StartFree с последующим ее изменением. На следующей схеме показаны три состояния базового массива для реализации списка на 10 элементов.
Состояние списка с шестью элементами: · Занятые ячейки массива: 3 – 1 – 2 – 8 – 10 – 5 ·
Состояние списка со всеми десятью элементами: · Занятые ячейки: 8 – 2 – 5 – 6 – 7 – 10 – 1 – 4 – 3 – 9 · Свободных ячеек нет: StartFree = -1
|