Вопросы_на_удовл.. Экзаменационные вопросы на удовлетворительно Знать наизусть следующие формулы (без доказательства) Первый замечательный предел

• Название: Экзаменационные вопросы на удовлетворительно Знать наизусть следующие формулы (без доказательства) Первый замечательный предел
• Дата: 09.03.2023
• Размер: 18.79 Kb.
• Имя файла: Вопросы_на_удовл..docx
• Тип: Экзаменационные вопросы; #977337

Экзаменационные вопросы на «удовлетворительно"

1. Знать наизусть следующие формулы (без доказательства):

1. 
   Первый замечательный предел.
   
2. 
   Второй замечательный предел.
   
3. 
   Таблица эквивалентных бесконечно малых.
   
4. 
   Таблица производных и правила дифференцирования.
   
5. 
   Формула производной сложной функции.
   
6. 
   Формула дифференциала первого порядка для функции , в случае, если х - независимая переменная и х – зависимая переменная.
   
7. 
   Формулы производной 1-го и 2-го порядка параметрически заданной функции.
   
8. 
   Формула Лейбница производной n-го порядка от произведения функций.
   
9. 
   Формула дифференциала n-го порядка для функции , если х - независимая переменная.
   
10. 
    Формула дифференциала второго порядка для функции , если х - зависимая переменная.
    
11. 
    Правила Лопиталя раскрытия неопределенностей.
    
12. 
    Таблица неопределенных интегралов.
    
13. 
    Формула Ньютона-Лейбница вычисления интеграла Римана.
    
14. 
    Формулы замены переменной в неопределенном и определенном интегралах.
    
15. 
    Формулы интегрирования по частям в неопределенном и определенном интегралах.
    
16. 
    Разложение правильной рациональной дроби на сумму простейших дробей.
    
17. 
    Дробно-рациональные подстановки, подстановки Чебышева.
    
18. 
    Универсальная тригонометрическая подстановка и дополнительные тригонометрические подстановки.
    
19. 
    Формулы вычисления площади плоской фигуры в декартовых, полярных координатах и в параметрическом виде.
    
20. 
    Формулы вычисления длины плоской дуги в декартовых, полярных координатах и в параметрическом виде.
    

2. Знать наизусть следующие определения и формулировки теорем (без доказательства):

1. 
   Определение предела числовой последовательности на языке «έ-N».
   
2. 
   Определение предела функции по Коши на языке «έ-δ».
   
3. 
   Определение бесконечно малой функции и определение ее порядка малости. определение эквивалентных бесконечно-малых функций.
   
4. 
   Определение непрерывности функции в точке на языке «έ-δ».
   
5. 
   Необходимое и достаточное условие непрерывности функции в точке. Классификация точек разрыва.
   
6. 
   Определение производной функции, ее геометрический смысл.
   
7. 
   Односторонние производные. Необходимое и достаточное условие существования производной.
   
8. 
   Определение дифференцируемой функции.
   
9. 
   Определение дифференциала и его геометрический смысл.
   
10. 
    Определение первообразной функции.
    
11. 
    Определение неопределенного интеграла.
    
12. 
    Определение интеграла Римана и его геометрический смысл.
    
13. 
    Необходимое условие экстремума функции.
    
14. 
    Первое достаточное условие экстремума функции.
    
15. 
    Необходимое и достаточное условие точки перегиба.
    

3. Уметь формулировать и доказывать следующие теоремы:

1. 
   Теорема о пределе суммы двух сходящихся числовых последовательностей.
   
2. 
   Теорема о связи бесконечно больших и бесконечно малых последовательностей. Свойства бесконечно малых последовательностей.
   
3. 
   Теорема о предельном переходе в неравенствах.6
   
4. 
   Теоремы о вычислении пределов с помощью таблицы эквивалентных бесконечно малых.
   
5. 
   Первая и вторая теоремы Коши для непрерывных функций.
   
6. 
   Правила вычисления производных от суммы функций.
   
7. 
   Доказать формулу вычисления производной обратной функции.
   
8. 
   Теорема о связи между непрерывностью и дифференцируемостью функции.
   
9. 
   Свойство инвариантности формы первого дифференциала.
   
10. 
    Вывести формулу 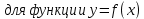, если х - зависимая переменная
    
11. 
    Вывести формула дифференциала n-го порядка для функции , если х - независимая переменная
    
12. 
    Достаточное условие монотонности функции.
    
13. 
    Теорема Коши (без доказательства) и теорема Лагранжа ( с доказательством) для дифференцируемых функций.
    
14. 
    Доказать формулу интегрирования по частям в неопределенном интеграле.
    
15. 
    Основная теорема интегрального исчисления (формула Ньютона-Лейбница).