Экз вопросы. Экзаменационные вопросы по курсу Гидрогазодинамика

Название	Экзаменационные вопросы по курсу Гидрогазодинамика
Дата	13.09.2022
Размер	5.09 Mb.
Формат файла
Имя файла	Экз вопросы.docx
Тип	Экзаменационные вопросы #674965

Экзаменационные вопросы по курсу «Гидрогазодинамика»

Основные определения гидростатики (поверхностные и массовые силы, гидростатическое давление).

Поверхностные силы (силы, пропорциональные поверхности, на которую они действуют) – силы воздействия окружающей жидкости на рассматриваемый объём.
Массовые силы (силы, пропорциональные массе жидкости) – силы, действие которых обусловлено внешним силовым полем (например, полем силы тяжести, электрическим, магнитным и т.д.).
Гидростатическое давление – это давление, производимое на жидкость силой тяжести.

Основное уравнение гидростатики. Закон Паскаля.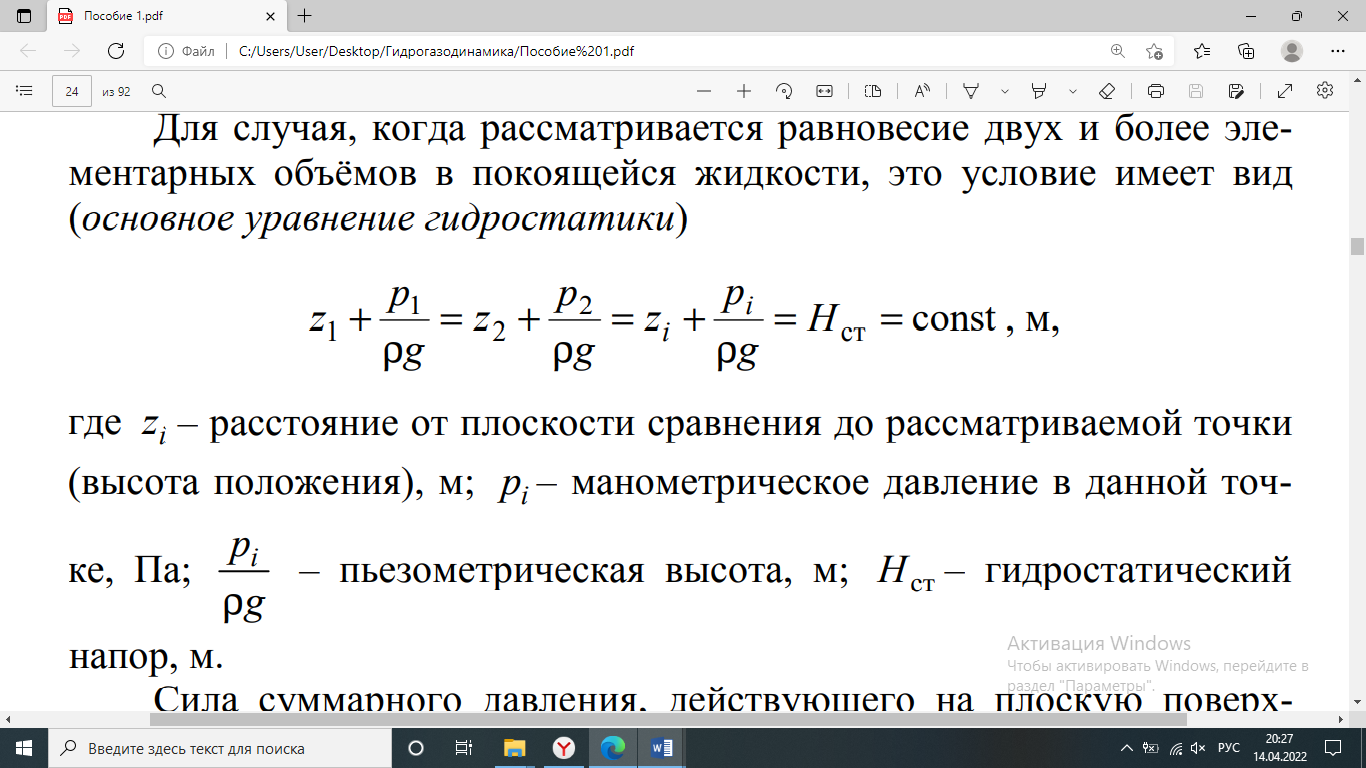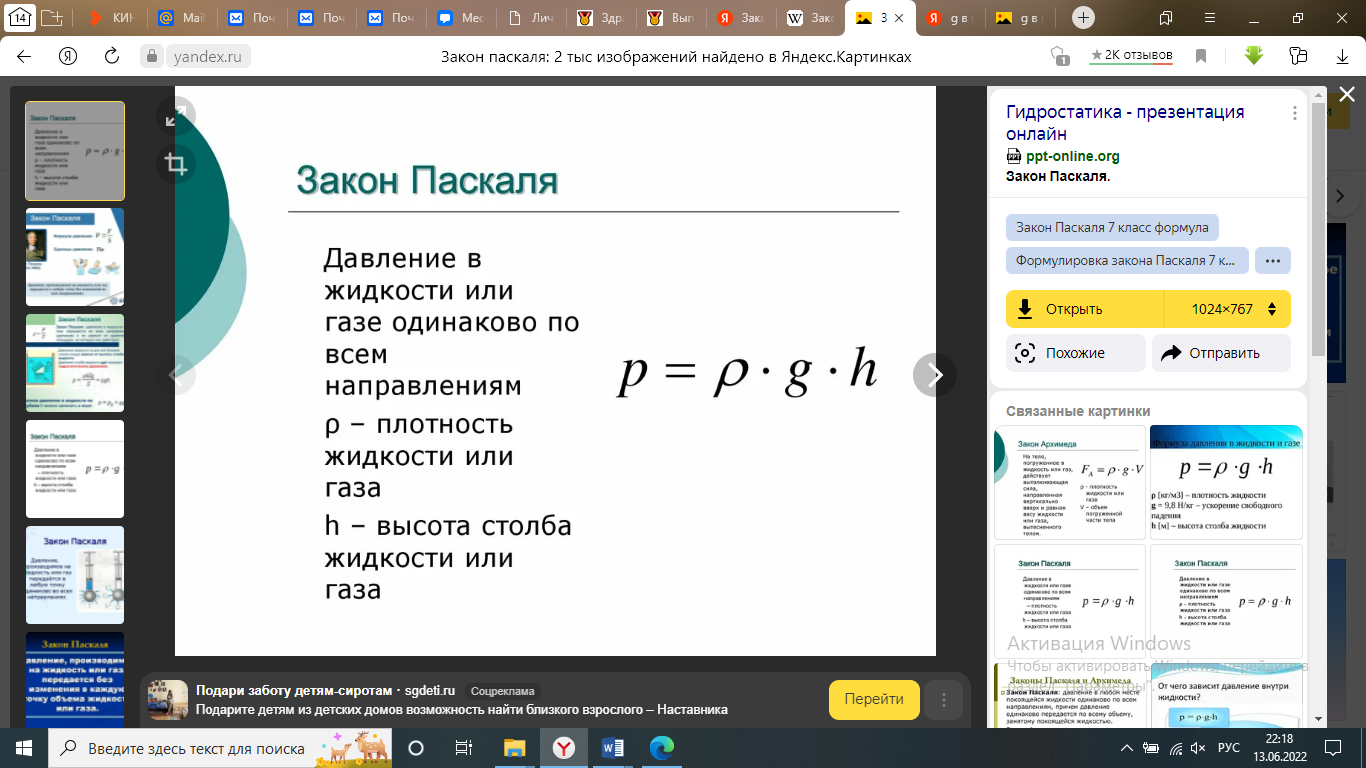

Силы, действующие в покоящейся жидкости на плоские стенки. Сила суммарного давления жидкости на плоские поверхности.

Силы, действующие в жидкости, делятся на массовые, объёмные и поверхностные
Массовые силы (силы, пропорциональные массе жидкости) – силы, действие которых обусловлено внешним силовым полем (например, полем силы тяжести, электрическим, магнитным и т.д.)
Объёмные силы (силы, пропорциональные объёму жидкости). Массовые и объёмные силы имеют одинаковое значение, если во всех точках исследуемого объёма среды её плотность не изменяется
Поверхностные силы (силы, пропорциональные поверхности, на которую они действуют) – силы воздействия окружающей жидкости на рассматриваемый объём. К поверхностным силам относятся силы давления и вязкости.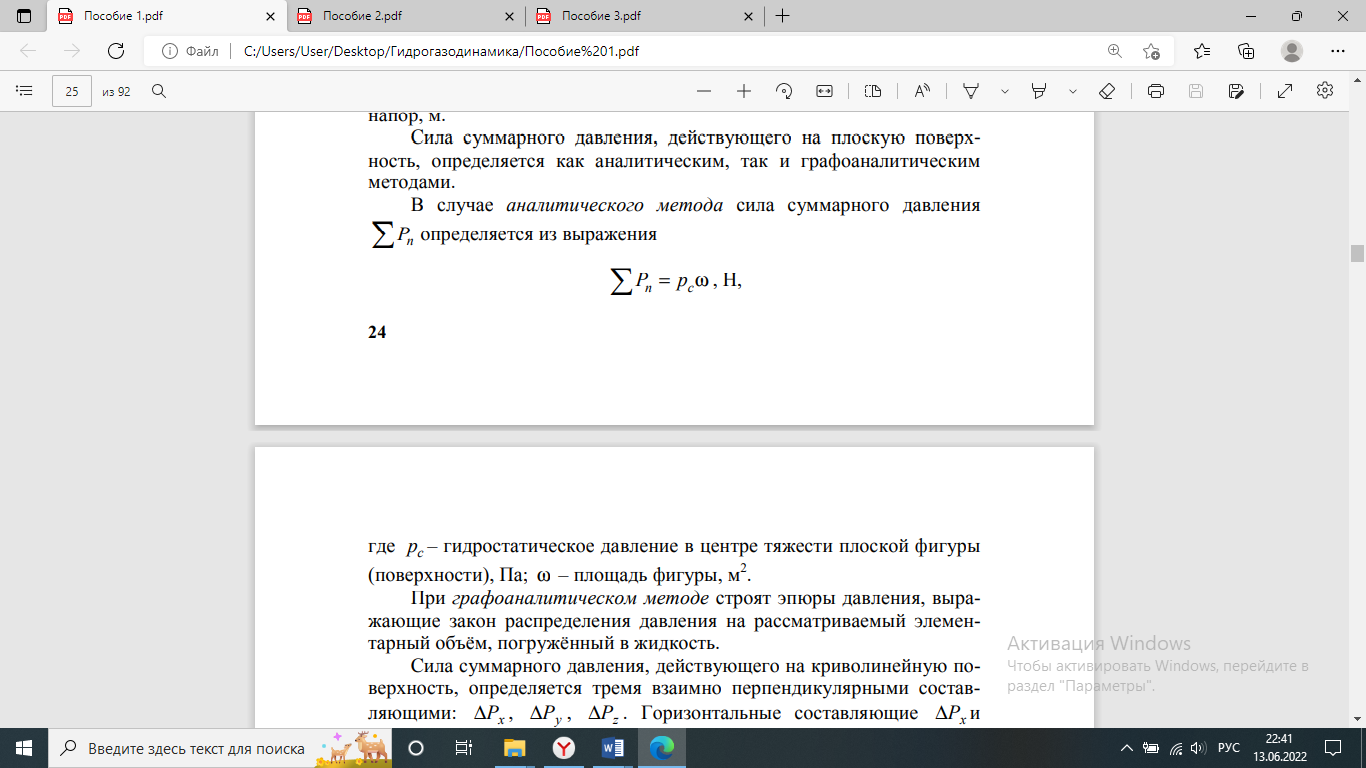

Сила суммарного давления жидкости на цилиндрические поверхности (центр давления, полная сила давления, объем тела давления).

Объем тела давления находят геометрически. При необходимости сложное тело давления можно разбить на элементарные и просуммировать их объемы.

Закон Архимеда и его приложения. Водоизмещение.

Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) - центром водоизмещения.

Методы и приемы изучения механики жидкости и газа.

Жидкость и газы представляют собой системы материальных точек (молекул, атомов). Состояние вещества является функцией давления и температуры.

В твёрдых телах кинетическая энергия движения молекул (атомов) недостаточна для выхода атомов из узлов кристаллической решётки, поэтому твёрдые тела сохраняют форму и объём.
В жидкостях кинетическая энергия молекул достаточна для выхода из узлов решётки и поэтому определённая часть молекул хаотически перемещается по всему объёму, но их энергия недостаточна для выхода за пределы жидкости, поэтому жидкости сохраняют объём, но не сохраняют форму, а принимают форму сосуда.
В газе энергия молекул достаточна для преодоления связей между молекулами, поэтому газы не сохраняют ни формы, ни объёма. Газ в беспредельном пространстве расширяется до бесконечности.

Молекулярная структура и особенности жидкого и газообразного состояний; силы притяжения и отталкивания.

В жидком состоянии вещество сохраняет объём, но не сохраняет форму. Это означает, что жидкость может занимать только часть объёма сосуда, но также может свободно перетекать по всей поверхности сосуда. Жидкое состояние обычно считают промежуточным между твёрдым телом и газом. Форма жидких тел может полностью или отчасти определяться тем, что их поверхность ведёт себя как упругая мембран

Газообразное состояние характерно тем, что оно не сохраняет ни форму, ни объём. Газ заполняет всё доступное пространство и проникает в любые его закоулки. Это состояние, свойственное веществам с малой плотностью. Переход из жидкого в газообразное состояние называют испарением, а противоположный ему переход из газообразного состояния в жидкое — конденсацией.
Силы притяжения Эти силы являются самыми значимыми для взаимодействия между частицами вещества. По своей природе они являются электростатическими.

Силы отталкивания начинают действовать, когда межмолекулярное расстояние сокращается до предельно возможного минимума. При таком сближении начинают соприкасаться внешние уровни электронов двух атомов. Как следует из принципа Паули, являющегося одним из базовых положений квантовой механики, заполненные электронные оболочки не могут проникать одна внутрь другой. Величина таких сил в значительной степени зависит от особенностей строения молекулы определенного вещества.

Основные уравнения кинетической теории газов.

Основное уравнение кинетической теории газов утверждает, что между давлением в газе p и средней кинетической энергией молекулы K существует простая связь: p  2/3 n  K , где n – концентрация молекул.

Основные физические свойства жидкостей. Определение жидкостей; плотность жидкостей; удельный вес; сжимаемость и температурные расширения жидкостей.

К основным физическим свойствам жидкости, которые рассматриваются в гидродинамике, относятся плотность, удельный вес, удельный объем, температурное расширение, сжимаемость и вязкость

Плотность — это отношение массы вещества к его объему:

р = m/V
Удельный вес — это отношение веса жидкости к занимаемому объему:

у = mg/V = pg.
Сжимаемость — свойство жидкости изменять объем при изменении давления
Температурное расширение — свойство жидкости изменять свой объем при изменении температуры. С ростом температуры объем жидкости увеличивается и наоборот. Различные жидкости при увеличении температуры на одну и ту же величину увеличиваются в объеме по разному.

Пластичные жидкости. Ньютоновские жидкости.

Пластичные жидкости в статических условиях ведут себя как твердые материалы, но при воздействии на них определенной силой они начинают течь. Минимальное усилие, которое необходимо приложить к системе, чтобы она начала течь называется предельным напряжением сдвига (f’).

Томатный кетчуп является ярким примером пластичных жидкостей: пока бутылку с продуктом не потрясти или ударить по ней, кетчуп течь не будет. После преодоления критического напряжения сдвига пластичные жидкости могут вести себ я как ньютоновские, псевдопластичные или дилатантные.

Жидкости, для которых вязкость не зависит от скорости деформации, называются ньютоновскими. Характерными ньютоновскими жидкостями являются вода и маловязкие моторные топлива.

Поведение ньютоновских жидкостей отлично видно на графиках зависимости напряжения сдвига (А) или вязкости (В) от скорости сдвига.

На практике это означает, что вязкость жидкости при данной температуре остается постоянной и не зависит от модели вискозиметра, шпинделя или скорости сдвига. Стандарты вязкости Brookfield являются также ньютоновскими жидкостями и подходять для всех моделей вискозиметров Brookfield.

Для неньютоновских жидкостей вязкость изменяется при изменении скорости сдвига. Для этих жидкостей модель вискозиметра, шпиндель и скорость сдвига влияют на конечный результат; для неньютоновских жидкостей измереяется, так называемая, «кажущаяся вязкость». Точности и воспроизводимости результатов для таких жидкостей можно достичь только при воспроизведении всех параметров измерений (модели вискозиметра, шпинделя, температуры и т.д.).

Гипотеза сплошности среды. Длина свободного пробега молекул.

Гипотеза сплошности: тело называется сплошным, если в любом бесконечно малом объеме содержится бесконечное количество материальных точек.
Длина свободного пробега молекулы — это среднее расстояние {\displaystyle \lambda }, которое пролетает частица за время между двумя последовательными столкновениями

Закон Ньютона. Динамическая вязкость. Кинематическая вязкость. Гипотеза Ньютона о вязкостном трении. Вязкость в условных градусах Энглера.

Первый закон Ньютона: закон инерции

Определение

Если на тело не действуют внешние силы, то покоящееся тело будет оставаться в покое, а движущееся тело останется в равномерном движении по прямой.

Второй закон Ньютона: основной закон динамики

Определение

Существует связь между силой (F), которая действует на тело (массы m), и ускорением (a). Тело приобретает ускорение из-за действующей на него силы.

Третий закон Ньютона: закон равенства действия и противодействия

Определение

На каждое действие существует равное и противоположное противодействие/реакция.

Динамическая вязкость

Динамическая вязкость определяет величину сопротивления текучести жидкости при перемещении ее слоя площадью 1 см2 на расстояние в 1 см со скоростью 1 см/сек. В СИ (Международной системе единиц) данный показатель измеряется в Па•с (паскаль•секунда). В системе же СГС единицей измерения вязкости является пуаз (в честь Ж. Пуазейля, французского физика).
Чем выше вязкость жидкости, тем, соответственно, больше время ее истечения. Например, чем дольше по времени краска, нефть, смола, мед или любая другая жидкая среда будет вытекать через воронку, тем больше будет вязкость данного вещества.
С точки зрения физики динамическая вязкость обозначает потерю давления за единицу времени (поэтому в системе СИ этот параметр и измеряется в Па•с). У жидкостей данный параметр снижается при росте температуры (то есть когда среда нагревается, она течет легче) и повышается при увеличении давления.

Кинематическая вязкость

Кинетическая вязкость — это соотношение коэффициента динамической вязкости жидкости к ее плотности. В системе СИ эта величина выражается в м2/с, а в системе СГС — в стоксах (Ст).
Кинетическая вязкость у жидкостей демонстрирует, насколько легко способно течь данное вещество. В практическом применении это связано с тем, насколько продукт густой. На данный показатель температура влияет несколько меньше, нежели на абсолютную вязкость, ведь тепло также уменьшает и плотность (при нагревании молекулы смещаются дальше друг от друга).

Условная вязкость (ВУ) - величина, косвенно характеризующая гидравлическое сопротивление течению, измеряемая временем истечения заданного объёма жидкости через вертикальную трубку определённого диаметра. Условная вязкость измеряется в градусах Энглера, и определяется отношением времени истечения 200 см3 испытываемой жидкости при данной температуре из специального вискозиметра ко времени истечения 200 см3 дистиллированной воды из того же прибора при +20 градусах Цельсия.

Поверхностное натяжение жидкостей, формула Лапласа. Поверхностное натяжение в капиллярных трубках.

Поверхностное натяжение жидкости:

В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:

a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);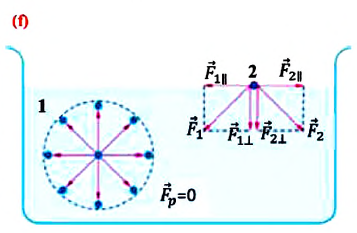

b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил

Свойства напряжений поверхностных сил.

1 св-во: напряжения поверхностных сил, действующих по произвольной площадке в данной точки жи/ти, зависят от девяти скалярных величин: 3 нормальных напряжений (Рхх , Руу, Рzz ) и 6 касательных (τху, τ xz, τyz, τyx, τzx, τzy). 2 св-во: если в жи/ти отсутствуют касательные напряжения, то нормальные напряжения в данной точке не зависят от ориентации площадки. 3 св-во: капельная жи/ть способна воспринимать произвольные сжимающие усилия (отрицательное нормальное напряжение) без разрыва сплошности. Однако жи/ть практически терпит разрыв при растяжении, то есть в ней могут провялятся лишь нормальные сжимающиеся усилия

Основные понятия о движении жидкости (живое сечение, смоченный периметр, расход, скорость, гидравлический радиус. Установившееся и неустановившееся движение).

Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения..
Смоченный периметр χ ("хи") - часть периметра живого сечения, ограниченное твердыми стенками
Расход потока Q - объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Гидравлический радиус потока R - отношение живого сечения к смоченному периметру

Установившееся – это такое движение, при котором его характеристики в лю-бой точке потока остаются неизменными во времени, средняя скорость υ, давление в любом сечении р, форма струи не меняются во времени.
Неустановившееся движение - это такое движение, когда скорость и давление в каждой точке изменяются с течением времени, т. е. являются функция-ми координат и времени.

Идеальная жидкость. Общая интегральная форма уравнений количества движения и момент количества движения.

Идеа́льная жи́дкость — в гидродинамике — воображаемая жидкость (сжимаемая или несжимаемая), в которой отсутствует вязкость. Из-за отсутствия вязкости в ней нет касательных напряжений между двумя соседними слоями жидкости^[1].

Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.

При решении некоторых задач МЖГ используется уравнение количества движения. Важнейшей особенностью этого уравнения является то, что для определения действующих сил не нужно знать существа процессов, происходящих внутри выделенного участка потока жидкости, нужно знать только параметры жидкости на границах участка. В механике твердого тела известна теорема об изменении количества движения. Она гласит: элементарное изменение количества движения некоторой массы m по какому-либо направлени. равно элементарному импульсу равнодействующей сил, приложенных к этой массе в том же направлении, т.е. d(mñ) = F dt,
Уравнение момента количества движения не является новым независимым уравнением гидрогазодинамики. Оно представляет новую форму уравнения движения, членами которого являются не силы и не количество движения, а моменты сил и моменты количества движения. Это уравнение широко используется при исследовании вращательного движения жидкости, является основным в теории турбомашин.

Уравнение момента количества движения для жидкого объема так же, как и для твердого тела, устанавливает, что момент равнодействующей внешних сил относительно произвольной оси равен полной производной по времени от суммарного момента количества движения относительно той же оси, т. е.

r	r		d	r r
∑F × r		=		(∑mc × r ),	(4.6)
∑F × r		=	dt	(∑mc × r ),	(4.6)
			dt

где r – радиусы векторы внешних сил и элементарных масс, имеющих скорости c ; mc × r – момент количества движения элементарной массы т.

Реальная жидкость. Интегральная форма количества движения и момента количества движения.

Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев).

Уравнение неразрывности течения (уравнение постоянства расхода).

Ламинарное и турбулентное течение жидкости. Критерий Рейнольдса.

Ламинарное (слоистое) течение – это такое течение, при котором слои жидкости текут, не перемешиваясь, скользя друг относительно друга. Ламинарное течение является стационарным, т.е. скорость течения в каждой точке пространства остается постоянной.

Турбулентное (вихревое) течение – это такое течение, при котором скорости частиц жидкости в каждой точке беспорядочно меняются. Турбулентное течение - это хаотическое, крайне нерегулярное, неупорядоченное течение жидкости.

Ламинарное течение жидкости в круглой трубе с прямой осью.
Турбулентное течение, гипотеза связи пульсационных составляющих со средней скоростью потока.
Установившееся и неустановившееся движение жидкости.

Линии тока и траектории.

Линией тока называется линия, касательная к каждой точке которой совпадает по направлению с вектором скорости в данный момент времени.

Семейство линий тока дает картину течения в данный момент времени, можно сказать, моментальный снимок направлений скоростей потока.

Через каждую точку пространства может проходить множество траекторий частиц, они могут пересекаться и пересекать сами себя.

Линии тока не пересекаются ни сами с собой, ни с другими линиями тока, так как вектор скорости в одной точке пространства не может иметь два разных значения в данный момент времени. Исключение составляют лишь особые точки, в которых скорость V = 0 (критические точки или точки торможения) или V = ∞ (исток, сток)

Необходимо четко представлять разницу между линией тока и траекторией движения частицы. Если траектория отражает изменение положения частицы с течением времени, то линия тока указывает направление скоростей разных частиц в один и тот же момент времени. И только при установившемся движении линия тока совпадает с траекторией частицы. В этом случае траектории всех частиц, проходящих через какую-либо точку пространства, будут одинаковыми, следовательно, в каждый момент времени все частицы, которые лежат на траектории, будут образовывать и линию тока. В случае неустановившегося движения линии тока и траектория частицы не совпадают.

Трубка тока (поверхность тока).

Трубка тока – простой и наглядный кинематический образ. Разбив весь поток на достаточно узкие трубки тока, можно, пользуясь основным свойством трубки – непроницаемостью ее боковой поверхности, изучать бесконечно малые перемещения выделенного объема жидкости. Между двумя произвольными линиями тока количество протекающей жидкости постоянно, поскольку вектор скорости лежит в касательной плоскости к поверхности трубки тока. То же самое можно сказать и о трубке тока: расход жидкости через любое сечение трубки тока одинаков.
Поверхность тока – поверхность, построенная для фиксированного момента времени, в каждой точке которой вектор скорости лежит в касательной плоскости. Если выделить в движущейся жидкости некоторый бесконечно малый замкнутый контур, через каждую точку которого можно провести линию тока, то совокупность всех линий тока образует замкнутую поверхность – трубку тока (рис. 2.2). Жидкость, движущуюся внутри трубки тока, называют элементарной струйкой.

Уравнение Д. Бернулли для движения идеальной жидкости.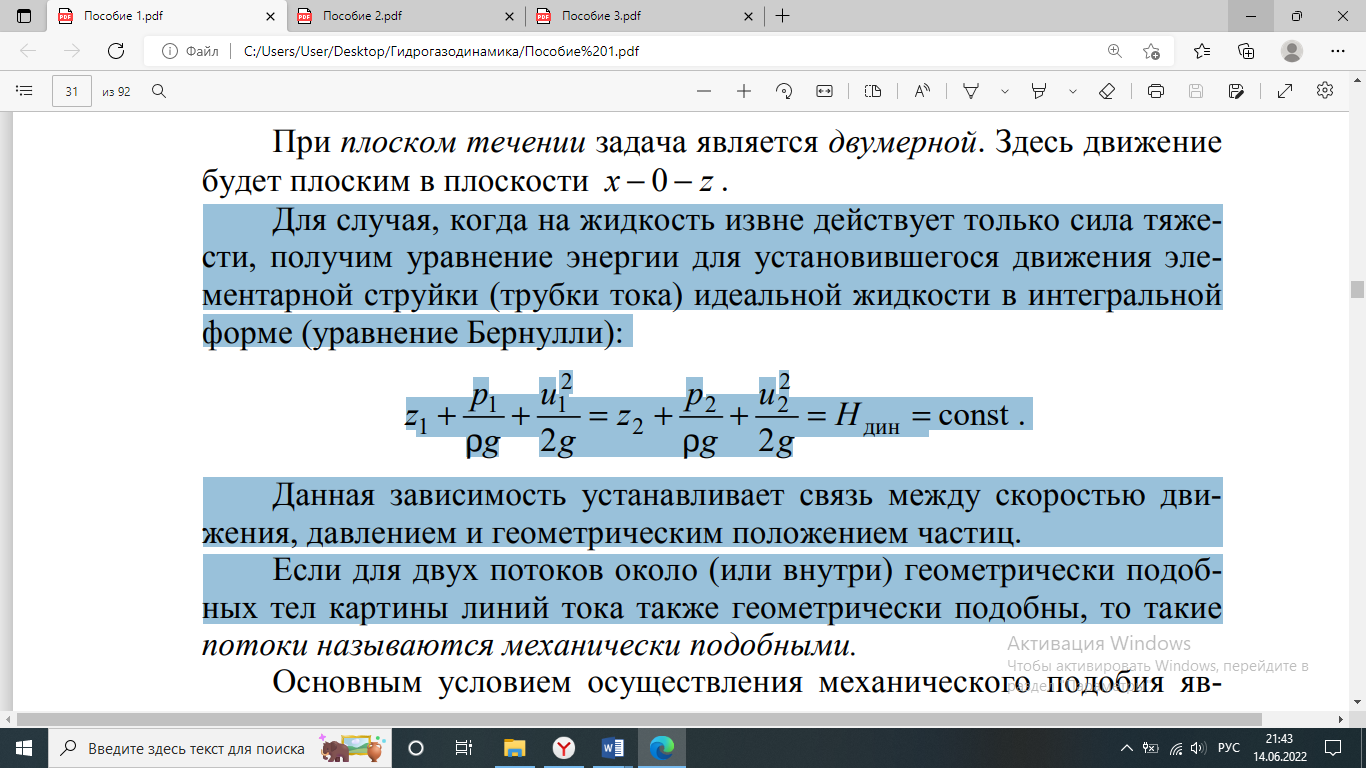

Уравнение Д. Бернулли для движения реальной жидкости. Физический и геометрический смысл уравнения Д. Бернулли.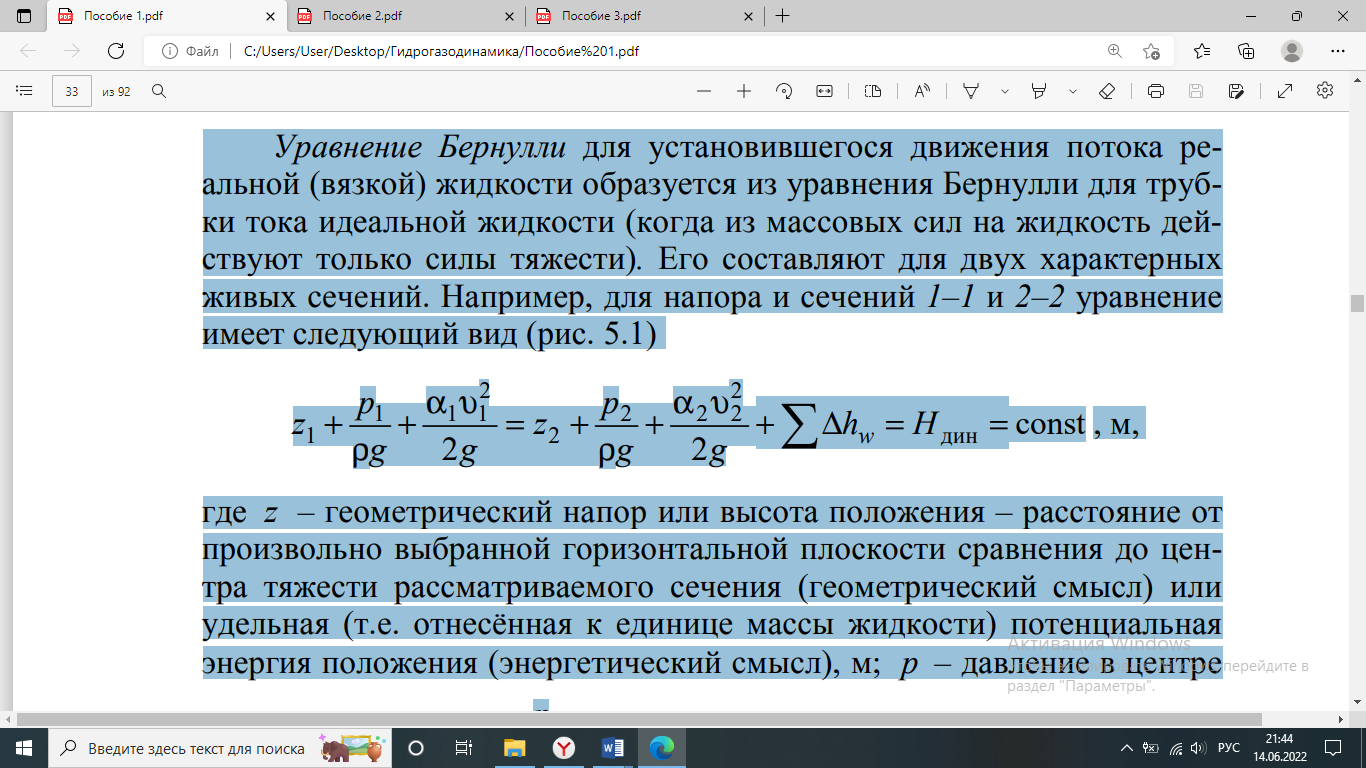

Одномерные потоки жидкости и газа.
Модели турбулентных течений. Уравнения Рейнольдса для турбулентных потоков.
Уравнения Навье-Стокса.
Измерение скорости потока в открытом канале и закрытых трубопроводах. Трубка Пиго- Прандтля.

Поток в открытом канале описывает случаи, когда верхняя поверхность текущей жидкости открыта для воздуха; поперечное сечение потока определяется только формой канала на нижней стороне и изменяется в зависимости от глубины жидкости в канале. Методы, подходящие для фиксированного поперечного сечения потока в трубе, не полезны в открытых каналах. Измерение расхода в водных путях является важным приложением для измерения расхода в открытых каналах; такие установки известны как измерители потока.

Level to flow[править/ править код]

Уровень воды измеряется в специально отведенной точке за водосливом или в лотке с использованием различных вспомогательных устройств (барботеры, ультразвуковые, поплавковые и дифференциальные давления являются распространенными методами). Эта глубина преобразуется в скорость потока в соответствии с теоретической формулой вида{\displaystyle Q=KH^{X}}, где {\displaystyle Q}- скорость потока, {\displaystyle K}- постоянная, {\displaystyle H}- уровень воды, и {\displaystyle X} показатель степени, который изменяется в зависимости от используемого устройства; или он преобразуется в соответствии с эмпирически полученными точками данных уровня / расхода ("кривая расхода"). Затем скорость потока может быть интегрирована с течением времени в объемный расход. Устройства от уровня до расхода обычно используются для измерения расхода поверхностных вод (родников, ручьев и рек), промышленных сбросов и сточных вод. Из них водосливы используются на потоках с низким содержанием твердых частиц (обычно поверхностных вод), в то время как желоба используются на потоках с низким или высоким содержанием твердых частиц.^[17]
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Трубка Пито - Прандтля - прибор для измерения скорости течения жидкости или газа, основанный на одновременном измерении полного и статического давлений в какой либо точке потока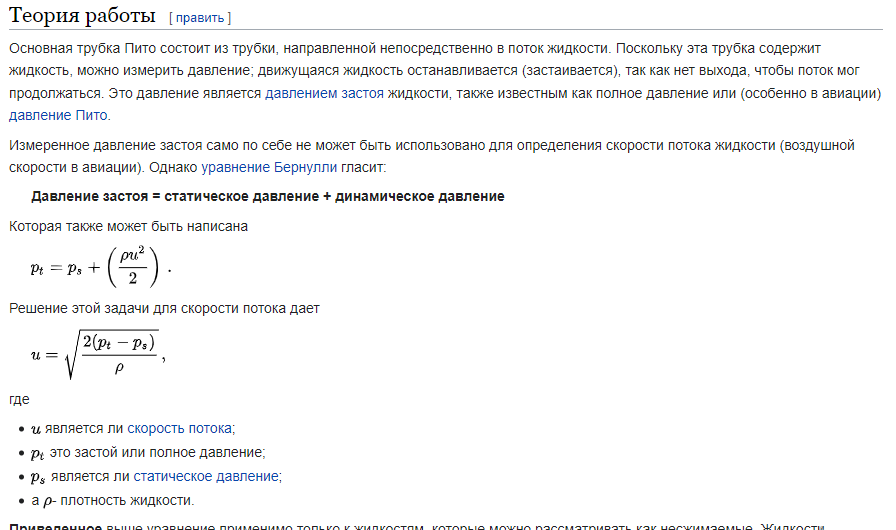

Измерение расхода потока в каналах произвольных сечений с помощью водомера Вентури.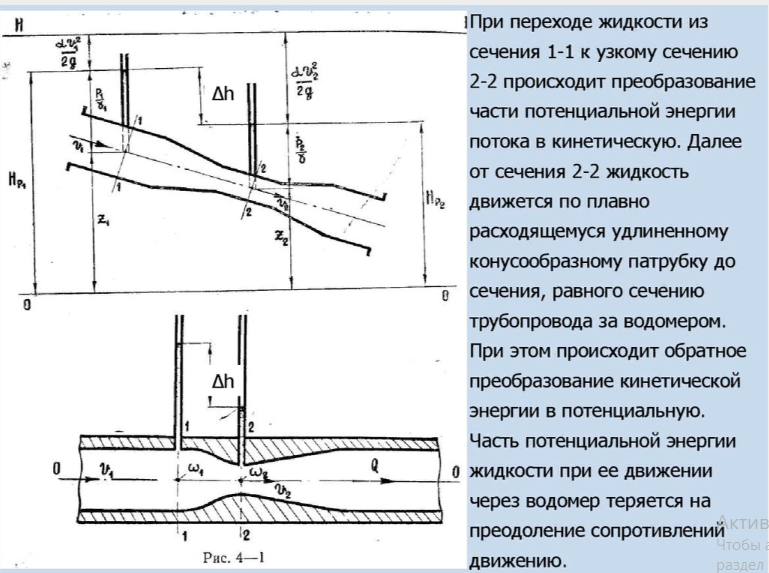

Гидравлические сопротивления. Потери напора на трение по длине трубопровода. Формула Дарси-Вейсбаха.

Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:

Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.

Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.

Основные понятия и определения пограничного слоя.

Пограничным слоем называется область течения, где силы вязкости соизмеримы с силами инерции. Различают пристенный пограничный слой (ПС) – слой жидкости, непосредственно прилегающий к твёрдой поверхности, и свободный ПС – аэродинамический след за обтекаемым телом, в котором силы вязкости существенны. Внешний поток – область течения, где можно пренебречь силами вязкости и считать жидкость идеальной. Уравнения, описывающие движение жидкости во внешнем потоке, более простые, чем уравнения Навье – Стокса, уравнения Эйлера.

Ламинарный пограничный слой на пластине.
Критическое число Рейнольдса. Отрыв пограничного слоя.

Отрыв пограничного слоя (англ. Boundarylayerseparation) — явление отсоединения слоя вязкого потока жидкости (газа) от обтекаемой им поверхности.

Точка отсоединения пограничного слоя называется точкой отрыва. В области между отсоединившимся пограничным слоем и обтекаемой поверхностью развивается возвратно-вихревое (не обязательно вязкое) течение.

Уравнение пограничного слоя в интегральной форме.
Переход ламинарного пограничного слоя в турбулентный.
Турбулентный пограничный слой на пластине.
Распределение скоростей по сечению потока. Особенности движения жидкости в началь ном участке трубы.

При ламинарном движении жидкости в цилиндрической трубе распределение скоростей по сечению имеет вид параболы и схематически изображается телескопическим (рис.): у стенок трубы скорости равны нулю, а при удалении плавно возрастают и достигают максимального значения на оси трубы.

Местные потери напора в трубах. Гидравлический удар.

Местные потери напора - это потери, обусловленные местными гидравлическими сопротивлениями, то есть такими элементами трубопроводов, в которых вследствие изменения поперечных размеров или конфигурации происходит деформация потока.

Гидравлический удар – это резкое повышение давления в трубопроводах и каналах с движущейся жидкостью при внезапном изменении скорости потока. Это сложный динамический волновой процесс образования упругих деформаций жидкости и их распространения по длине трубопровода.

Гидравлический удар создает ударную волну в виде распространяющегося в жидкости фронта резкого, почти мгновенного изменения ее параметров — давления и скорости. С явлением гидравлического удара приходится сталкиваться при быстром срабатывании задвижек, когда резкое прекращение тока жидкости вызывает в трубопроводе волну повышенного давления, что зачастую приводит к разрыву стенок.

Потери напора при внезапном (резком) изменении сечения трубопровода.

Расчет длинных трубопроводов при квадратичном законе сопротивления.
П 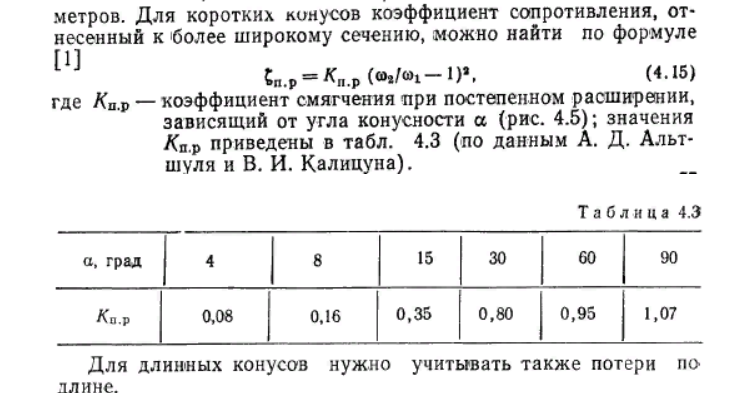отери напора при постепенном изменении сечения трубопровода.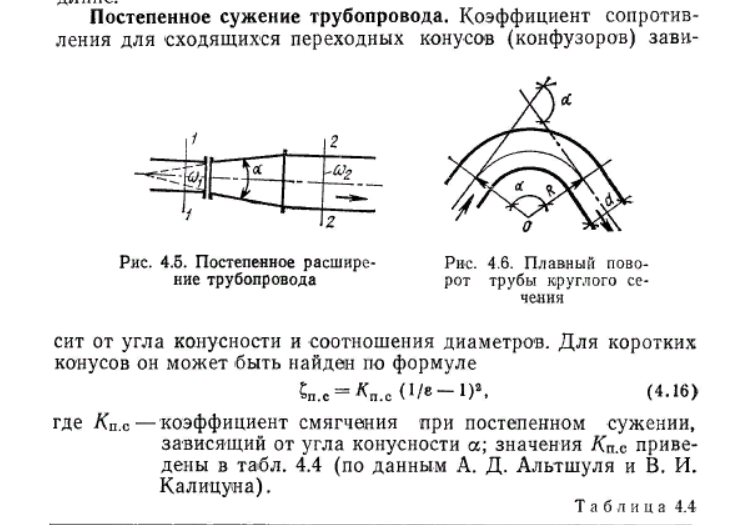

Потери напора при повороте трубы.

Местные потери в трубах при малых числах Рейнольдса. Взаимное влияние местных со противлений.

Кавитация в местных сопротивлениях.

Простые трубопроводы. Методика расчета.

Трубопровод называют простым, если жидкость транспортируется по нему от питателя к приемнику без ответвлений потока, но может иметь различные диаметры и включать местные сопротивления.
Имеем простой трубопровод с постоянным диаметром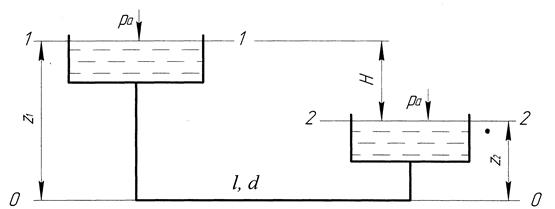

, который работает под напором

Рис. 41 Схема расчета прямого трубопровода (случай первый)

Для сечений 1 - 1 и 2 - 2 напишем уравнение Бернулли:

.

Так как

, давление

, тогда уравнение примет вид:

(119)

Так как мы имеем гидравлически длинный трубопровод, то пренебрегая местным сопротивлением, получим

(120)

где

Сложные трубопроводы. Методика расчета.

Трубопроводы, содержащие последовательные, параллельные соединения и разветвления простых трубопроводов называются сложными.
Гидравлический расчет трубопроводов производят по методикам:

1) удельных гидравлических сопротивлений;

2) удельных потерь напора на трение;

3) приведенного коэффициента местного сопротивления на трение;

4) приведения местных сопротивлений к линейным.

Истечение жидкостей через отверстия и насадки.

Истечение жидкости через отверстие может происходить при постоянном и переменном напоре. Если истечение жидкости через отверстие происходит в атмосферу или другую газовую среду, то такое отверстие называется незатопленным. Если же истечение идет под уровень, а не в атмосферу – затопленным.

При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи. Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.

При истечении жидкости, через отверстие в тонкой стенке на некотором расстоянии от стенки (l = d_o), происходит сжатие струи. Площадь живого сечения струи будет меньше площади отверстия. Это объясняется тем, что частицы жидкости при входе в отверстие имеют скорости различных направлений.
С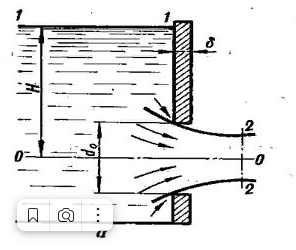

труя отрывается от стенки у кромки отверстия и затем несколько сжимается. Цилиндрическую форму струя принимает на расстоянии, равном примерно одному диаметру отверстия. Сжатие струи обусловлено необходимостью плавного перехода от различных направлений движения жидкости в резервуаре, в том числе от радиального движения по стенке, к осевому движению струи.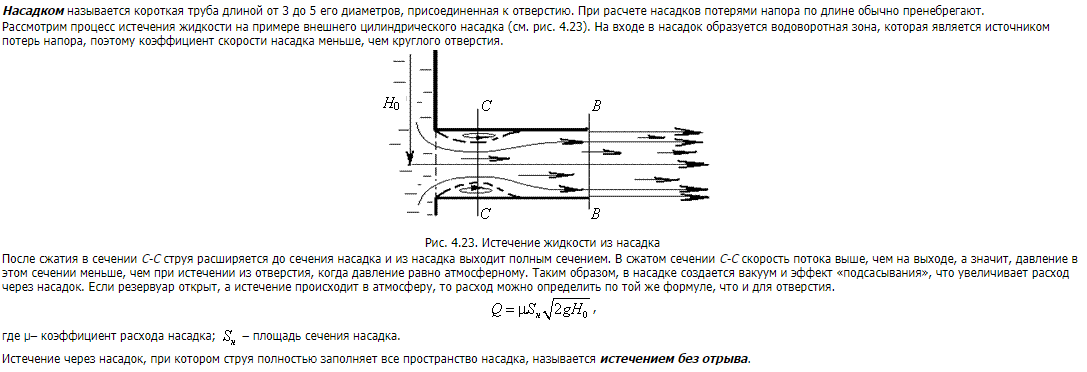

Определяющие параметры газовых потоков. Скорость звука.

Параметры газового потока ( скорость, давление, температура) по окружности газового тракта всегда имеют некоторую неравномерность. Такой же след оставляют разделительные стойки на входе в компрессор. Температура газа обычно имеет несколько пиков, соответствующих числу камер сгорания. К неравномерности параметров газового потока приводит также несимметричность входа в компрессор, наличие окон для отбора или перепуска воздуха, стойки на выходе из турбины, ограниченные размеры испытательного бокса и другие конструктивные особенности установки.
Скорость звука — скорость распространения упругих волн в среде: как продольных (в газах, жидкостях или твёрдых телах), так и поперечных, сдвиговых (в твёрдых телах).

Определяется упругостью и плотностью среды: как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях — меньше, чем в твёрдых телах. Также в газах скорость звука зависит от температуры данного вещества, в монокристаллах — от направления распространения волны.

Обычно не зависит от частоты волны и её амплитуды; в тех случаях, когда скорость звука зависит от частоты, говорят о дисперсии звука.

Сопло Лаваля для получения сверхзвуковых скоростей.
Прямые скачки уплотнения.
Косые скачки уплотнения.
Тепловые и конденсационные скачки в потоке.
Основы расчетов двухкомпонентных и двухфазных течений, фазовое равновесие в потоке.