|
|
Экзаменационные билеты по коллоидной химии. Экзаменационный билет 1
Факторы агрегативной устойчивости лиофобных дисперсных систем. Электролитная коагуляция (концентрационная и нейтрализационная коагуляция). Правило Шульце-Гарди и закон Дерягина. Способы стабилизации лиофобных дисперсных систем.
Различают следующие термодинамические и кинетические факторы агрегативной устойчивости дисперсных систем:
1. Электростатический фактор заключается в уменьшении межфазного натяжения вследствие возникновения двойного электрического слоя на поверхности частиц в соответствии с уравнением Липпмана.
2. Адсорбционно-сольватный фактор состоит в уменьшении межфазного натяжения при взаимодействии частиц дисперсной фазы со средой (благодаря адсорбции и сольватации)
3. Энтропийный фактор, как и первые два относится к термодинамическим. Он дополняет первые два фактора и действует в системах, в которых частицы или их поверхностные слои участвуют в тепловом движении.
4. Структурно-механический фактор является кинетическим. Его действие обусловлено тем, что на поверхности частиц имеются пленки, обладающие упругостью и механической прочностью, разрушение которых требует затраты энергии и времени.
5. Гидродинамический фактор снижает скорость коагуляции благодаря изменению вязкости среды и плотности дисперсной фазы и дисперсионной среды.
6. Смешанные факторы наиболее характерны для реальных систем. Обычно агрегативная устойчивость обеспечивается несколькими факторами одновременно.
Коагуляция протекает в термодинамически неустойчивых (лиофобных) дисперсных системах, и об агрегативной устойчивости таких систем судят по скорости коагуляции.
Коагуляция может происходить как без внешнего воздействия на систему, так и при повышении температуры, межаническом, электрическом или другом воздействии, а в случае золей – при ведении коагулянтов, например электролитов.
Принято считать, что типичные лиофобные системы агрегатнвно устойчивы благодаря проявлению электростатического фактора стабилизации и коагулируют при введении в систему сравнительно небольших количеств любых электролитов. Наименьшая концентрация электролита см, при которой начинается коагуляция (медленная), называется порогом коагуляции. Для осуществления быстрой коагуляции требуется такая концентрация электролита сб, после увеличения которой скорость коагуляции остается постоянной (когда фактор устойчивости W=1, или потенциальный барьер ΔE = 0).
З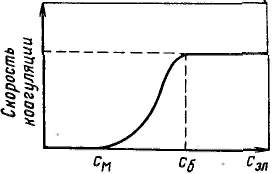 ависимость скорости коагуляции от концентрации электролита показана на рисунке. Из этого рисунка следует, что введение электролита в дисперсную систему снижает потенциальный барьер, который при быстрой коагуляции (максимальной скорости) становится равным нулю. Порог коагуляции существенно зависит от момента его фиксирования, от метода наблюдения за коагуляцией (изменение интенсивности рассеяния света, реологических свойств и др.) и от концентрации золя, поэтому необходимо всегда подробно указывать условия определения этой величины. ависимость скорости коагуляции от концентрации электролита показана на рисунке. Из этого рисунка следует, что введение электролита в дисперсную систему снижает потенциальный барьер, который при быстрой коагуляции (максимальной скорости) становится равным нулю. Порог коагуляции существенно зависит от момента его фиксирования, от метода наблюдения за коагуляцией (изменение интенсивности рассеяния света, реологических свойств и др.) и от концентрации золя, поэтому необходимо всегда подробно указывать условия определения этой величины.
В соответствии с теорией ДЛФО введение электролита в дисперсную систему вызывает сжатие двойного электрического слоя на поверхности частиц, вследствие чего они могут подойти друг к другу на расстояния, на которых преобладают силы притяжения. Уменьшение толщины двойного слоя сопровождается обменом противоионов этого слоя на вызывающие коагуляцию ионы электролита.
Закон Дерягина: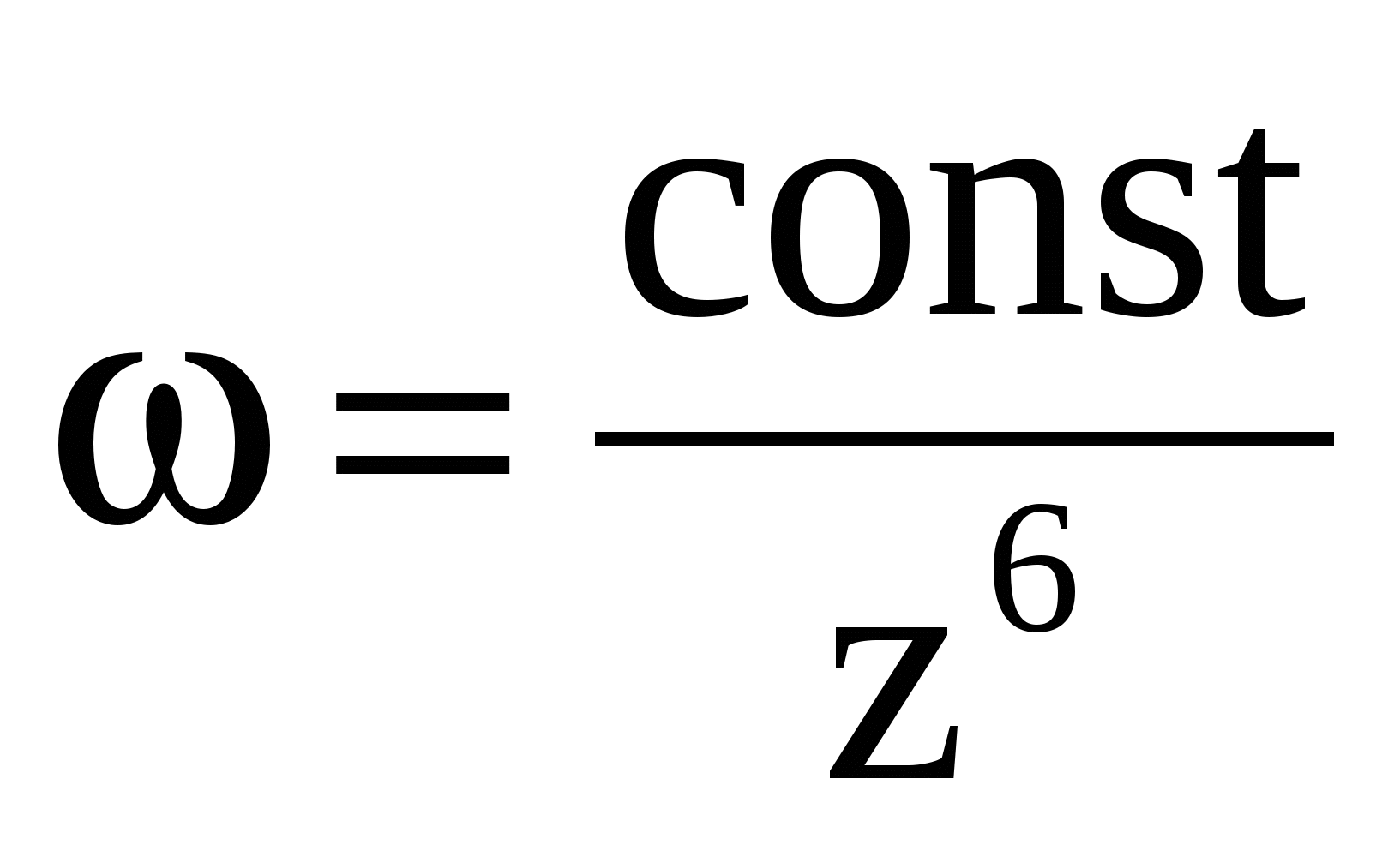
При высоких потенциалах порог быстрой коагуляции по теории ДЛФО не зависит от потенциала и обратно пропорционален заряду противоиона в шестой степени, что хорошо обосновывает известное эмпирическое правило Шульце — Гарди. По правилу Шульце — Гарди значения порогов коагуляции для электролитов с зарядами противоионов 1, 2, 3 находятся в соотношении 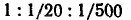 . .
Чтобы обеспечить агрегативную устойчивость дисперсных систем, частицы которых имеют лиофобную поверхность, применяют стабилизаторы, способствующие увеличению межфазного взаимодействия. В качестве таких стабилизаторов широко применяют ПАВ и ВМС (имеющие неполярные и полярные части молекул), лиофилизируюшие поверхность частиц дисперсной фазы.
Стабилизацию лиофобных дисперсных систем с помощью лнофильных коллоидов (в первую очередь, ВМС) называют защитным действием стабилизаторов — коллоидной защитой.
Определите удельную поверхность (м2/г) порошка сульфата бария, если известно, что его частицы сферической формы оседают в водной среде с высоты 22,6 см за 1350 секунд. Плотность сульфата бария равна 4,5 г/см3, плотность и вязкость воды составляют 1 г/см3 и 10-3 Па·с, соотвстственно.

Экзаменационный билет № 15
Особенности адсорбции ПАВ на границе раздела раствор-воздух. Зависимость поверхностного натяжения от состава раствора при соблюдении закона Генри. Поверхностное натяжение адсорбционной пленки. Уравнение состояния двумерного газа на поверхности жидкости; различные агрегатные состояния адсорбционных пленок. Весы Ленгмюра и определение размеров молекул ПАВ.
Поверхностно-активные вещества (ПАВ), молекулы которых имеют дифильное строение и включают большой углеводородный радикал, отличаются высокой поверхностной активностью по отношению к воде, что отражает сильную зависимость поверхностного натяжения водного раствора ПАВ от их концентрации. Большие значения поверхностной активности предполагают пренебрежимо малые концентрации ПАВ в объеме раствора по сравнению с концентрацией их в поверхностном слое, т. е. с величиной их адсорбции на границе раствор — воздух. Подобная зависимость может обнаруживаться и в растворах других веществ на границе с жидкостью или твердым телом, например при специфическом взаимодействии с поверхностью. Отмеченная особенность позволяет пренебречь разницей между величиной адсорбции А и величиной гиббсовской адсорбции Г, т. е. ГА. Из этого соотношения следует, что для растворов ПАВ все уравнения адсорбции, включающие величину адсорбции А, будут также справедливы, если заменить А на Г. Одним из таких уравнений является выражение закона Генри, который характеризует адсорбцию при малых концентрациях.
Применительно к адсорбции неионогенных (недиссоциирующих) ПАВ закон Генри запишется так: 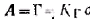
В такой записи закон Генри можно сопоставить с адсорбционным уравнением Гиббса:
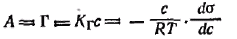
Р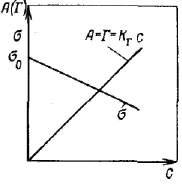 азделим переменные и проведя интегрирование полученного уравнения в пределах от σ0 (поверхностное натяжение чистого растворителя) до σ и соответственно от с = 0 до с. Получим азделим переменные и проведя интегрирование полученного уравнения в пределах от σ0 (поверхностное натяжение чистого растворителя) до σ и соответственно от с = 0 до с. Получим 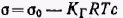 . .
Таким образом, в области действия закона Генри поверхностное натяжение линейно уменьшается с увеличением концентрации неионогенного ПАВ.
При адсорбции или растекании вещества на поверхности образуется поверхностная (адсорбционная) пленка этого вещества. Полученные ранее уравнения изотерм поверхностного натяжения для ПАВ позволяют перейти к уравнениям состояния поверхностных пленок. При очень малых концентрациях ПАВ распределение вещества между раствором и поверхностным слоем описывается законом Генри, а зависимость поверхностного натяжения от концентрации следует указанному выше соотношению. Если в этом соотношении обозначить 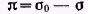 и учесть адсорбционное уравнение, то получим: и учесть адсорбционное уравнение, то получим: 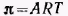
Так как величина А обозначает число молей адсорбированного вещества, приходящееся на единицу поверхности, а обратная ей величина Sм=l/A выражает поверхность, на которой распределен 1 моль адсорбированного вещества, то полученному соотношению можно придать вид: 
Это уравнение аналогично, уравнению состояния идеального газа. Различие состоит в том, что вместо объема 1 моль газа здесь выступает поверхность, занимаемая 1 моль ПАВ, а вместо давления газа — разность поверхностных натяжений, которая получила название давления двухмерного газа, или двухмерного давления. В соответствии с этим полученное соотношение называют уравнением состояния идеального двухмерного газа.
В зависимости от условий, природы ПАВ и подложки образуются поверхностные пленки, которые по свойствам подобны веществам в трех агрегатных состояниях — газообразном, жидком и твердом.
Как известно, 1 мономолекулярный слой (пленка) может образоваться только в том случае, если работа адгезии больше работы когезии растекающегося вещества (коэффициент растекания имеет положительный знак). Если подложка жидкая и наблюдается взаимное насыщений фаз, растекание может перейти в нерастекание — пленка соберется в линзу.
В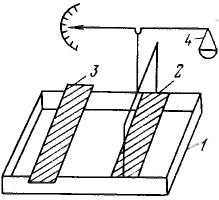 озможность существования поверхностных пленок в различных агрегатных состояниях впервые было наглядно показано Ленгмюром. Он специально сконструировал весы для измерения поверхностного (двухмерного) давления. Принцип метода измерения состоит в следующем. В кювету 1 наливают до краев подлежащую жидкость и на ее поверхность между неподвижной 2 и подвижной 3 планками наносят вещество, образующее мономолекулярную пленку. В процессе теплового движения молекулы вещества ударяются о планку и создают давление, которое можно уравновесить и измерить с помощью разновесов в чашечке 4. Передвигая планку 3, можно изменять площадь, занимаемую молекулами пленки, и тем самым изменять ее двухмерное давление. озможность существования поверхностных пленок в различных агрегатных состояниях впервые было наглядно показано Ленгмюром. Он специально сконструировал весы для измерения поверхностного (двухмерного) давления. Принцип метода измерения состоит в следующем. В кювету 1 наливают до краев подлежащую жидкость и на ее поверхность между неподвижной 2 и подвижной 3 планками наносят вещество, образующее мономолекулярную пленку. В процессе теплового движения молекулы вещества ударяются о планку и создают давление, которое можно уравновесить и измерить с помощью разновесов в чашечке 4. Передвигая планку 3, можно изменять площадь, занимаемую молекулами пленки, и тем самым изменять ее двухмерное давление.
По зависимости поверхностного давления пленки от площади поверхности, приходящейся на 1 молекулу (1 моль) вещества пленки, можно судить о состоянии пленки.
Резкое увеличение поверхностного давления при сжатии пленки отвечает образованию сплошного мономолекул яркого слоя, в котором молекулы плотно прижаты друг к другу. Если площадь sм0, на которой размещен таким образом 1 моль вещества, разделить на число Авогадро, то получим площадь, непосредственно занимаемую одной молекулой:
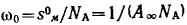
Структурообразованне по теории ДЛФО. Коагуляционно-тиксотропные и конденсационно-кристаллизацнонные структуры. Переход одних структур в другие. Классификация дисперсных систем по реологическим свойствам.
Под структурой тел обычно понимают пространственное взаимное расположение составных частей тела: атомов, молекул, мелких частиц. Структура разбавленных агрегативно устойчивых дисперсных систем по ряду свойств очень похожа на структуру истинных растворов. Основное отличие состоит в том, что в дисперсных (гетерогенных) системах частицы дисперсной фазы и молекулы дисперсионной среды сильно различаются по размерам. Увеличение концентрации дисперсной фазы приводит к взаимодействию ее частиц, подобному ассоциации молекул и ионов в истинных растворах. Изменение свойств дисперсных систем с ростом концентрации происходит постепенно до тех пор, пока не наступит коагуляция частиц. В коллоидной химии понятия структуры и структурообразования принято связывать именно с коагуляцией. В процессе коагуляции происходит образование пространственной структурной сетки из частиц дисперсной фазы, что резко увеличивает прочность системы.
Таким образом, структурообразование в свободнодисперсных системах есть результат потери их агрегативной устойчивости. По мере увеличения прочности структуры свободнодисперсная система переходит в связнодисперсную систему. Появление и характер образующихся структур, как правило, определяют по механическим свойствам систем, к важнейшим из которых относятся вязкость, упругость, пластичность, прочность. Так как эти свойства непосредственно связаны со структурой тел, то их обычно называют структурно-механическими.
Анализ многообразных свойств структур в дисперсных системах позволил П. А. Ребиндеру разделить их на два основных класса, различающихся по видам взаимодействия частиц дисперсной фазы. Исходя из того, что коагуляция соответствует первичному и вторичному минимуму потенциальной кривой взаимодействия частиц, он предложил различать конденсационно-кристаллизационные и коагуляционные структуры. Конденсационно-кристаллизационное структурообразование, отвечающее коагуляции в первичном потенциальном минимуме, осуществляется путем непосредственного химического взаимодействия между частииами и их срастания с образованием жесткой объемной структуры. Если частицы аморфные, то структуры, образующиеся в дисперсных системах, принято называть конденсационными, если частицы кристаллические, то структуры являются кристаллизационными. При непосредственном срастании частиц механические свойства структур соответствуют свойствам самих частиц. Конденсационно-кристаллизационные структуры типичны для связнодисперсных систем, т. е. систем с твердой дисперсионной средой. Такие структуры придают телам прочность, хрупкость и не восстанавливаются после разрушения.
Под коагуляционными структурами понимают структуры, которые образуются при коагуляции, соответствующей вторичному минимуму потенциальной кривой взаимодействия частиц дисперсной фазы (хотя конденсационно-кристаллизационные структуры также формируются в результате коагуляции). При образовании коагуляционньтх структур взаимодействие частиц, осуществляемое через прослойки дисперсионной среды, является, как правило, ван-дер-ваальсовым, и поэтому пространственный каркас такой структуры не может отличаться высокой прочностью. Механические свойства коагуляционных структур определяются не столько свойствами частиц, образующих структуру, сколько характером и особенностями межчастичных связей и прослоек среды. Коагуляционные структуры имеют обычно жидкую дисперсионную среду. Для них характерна способность восстанавливать структуру во времени после ее механического разрушения. Это явление получило название тиксотропии. Соответственно подобные структуры часто еще называют коагуляционно-тиксотропными.
Самопроизвольное восстановление коагуляционной структуры свидетельствует о том, что она обладает наибольшей механической прочностью при относительном минимуме энергии Гиббса. Такое соответствие отсутствует у конденсационно-кристаллизационных структур, которые образуются обычно в условиях высоких пересыщений и поэтому термодинамически неустойчивы. Их высокая прочность обеспечивается одновременным уменьшением пересыщения и снижением внутренних напряжений.
Имеются классификации тел, основанные на их реологических свойствах. В соответствии с этими свойствами все реальные тела принято делить на жидкообразные (предел текучести равен нулю, Рт = 0) и твердообразные (Рт>0).
Жидкообразные тела классифицируют на ньютоновские и неньютоновские жидкости. Ньютоновскими жидкостями называют системы, вязкость которых не зависит от напряжения сдвига и является постоянной величиной в соответствии с законом Ньютона. Течение неньютоновских жидкостей не следует закону Ньютона, их вязкость зависит от напряжения сдвига. В свою очередь, они подразделяются на стационарные, реологические свойства которых не изменяются со временем, и нестационарные, для которых эти характеристики зависят от времени. Среди неньютоновских стационарных жидкостей различают псевдопластические и дилатантные.
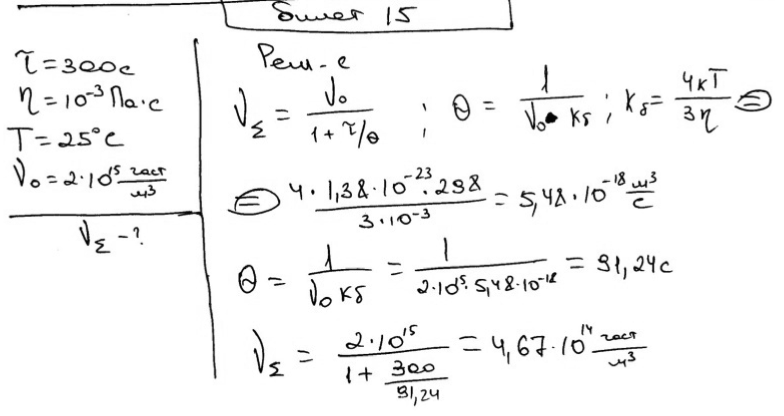
Рассчитайте концентрацию частиц гидрозоля золота через 300 с от начала быстрой коагуляции, если начальная концентрация составляла 2·1015 частиц/м3; вязкость дисперсионной среды 10-3 Па·с при 25 ºС.
Экзаменационный билет № 16
Поверхностное натяжение: термодинамическое определение, физический смысл, влияние природы взаимодействующих фаз. Вывод уравнения для полной (внутренней) энергии поверхностного слоя (уравнение Гиббса- Гельмгольца). Зависимость термодинамических параметров поверхности от температуры.
Есть несколько определений поверхностного натяжения:
Поверхностное натяжение – работа образования новой поверхности в изотермическом процессе
Поверхностное натяжение – сила, действующая по периметру данной поверхности, отнесенная к единице длины.
Поверхностное натяжение – работа переноса молекул из объема тела на поверхность.
Термодинамическое определение поверхностного натяжения:
Термодинамическое определение поверхностного натяжения вытекает из объединенного уравнения первого и второго начал термодинамики. Запишем его для гетерогенной системы относительно изменения внутренней энергии U:

При постоянных S, V, ni и q имеем:
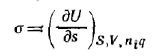
т. е. поверхностное натяжение есть частная производная от внутренней энергии по площади поверхности раздела фаз при постоянных энтропии, объеме, числе молей компонентов и заряде.
Так как объединенное уравнение первого и второго начал термодинамики может быть записано и относительно других термодинамических потенциалов, а именно энергии Гиббса G, энергии Гельмгольца F и энтальпии Я, то при соответствующих постоянных параметрах получим:
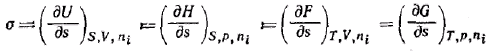
Таким образом, поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянных соответствующих параметрах.
Физический смысл поверхностного натяжения можно представить так: поверхностное натяжение на границе жидкости с газовой фазой – работа, расходуемая на обратимый разрыв столбика этой жидкости с поперечным сечением в 0,5 единицы площади, так как при разрыве образуется новая поверхность, равная единице площади.
Чем сильнее межмолекулярные связи в данном теле, тем больше его поверхностное натяжение на границе с газовой фазой.
В соответствии со вторым началом термодинамики избыточная энтропия равна
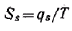
Учитывая, что Gs = σ, получим следующее выражение:
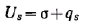
Из этого уравнения следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности. Для индивидуальных веществ теплота qs всегда положительна, так как при образовании поверхности теплота поглощается. Из уравнения объединенных первого и второго начала термодинамики при постоянстве всех параметров, кроме температуры, имеем:

Подставлям это выражение в полученные уравнения:

Это уравнение называется уравнением Гиббса — Гельмгольца. Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностным натяжением). Из этого уравнения следует, что для определения полной поверхностной энергии необходимо знать зависимость поверхностного натяжения от температуры. Для индивидуальных веществ теплота qs всегда положительна, а это значит, что температурный коэффициент поверхностного натяжения отрицателен:
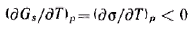
Таким образом, поверхностное натяжение индивидуальных веществ на границе с газом (воздухом) снижается с повышением температуры. Для большинства неполярных жидкостей эта зависимость линейная.
Реологический метод исследования структур в дисперсных системах. Реологические модели идеальных тел (модели Гука, Сен-Венана-Кулона). Кривые течения реальных жидкостей и твердообразных структуртрованных систем.
Структурно-механические свойства систем исследуют методами реологии — науки о деформациях и течении материальных систем. Реология изучает механические свойства систем по проявлению деформации под действием внешних напряжений. В коллоидной химии методы реологии используют для исследования структуры и описания вязкотекучих свойств дисперсных систем.
В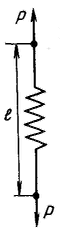 реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат три основных идеальных закона, связывающих напряжение с деформацией. Им соответствуют три элементарные модели (элемента) идеализированных материалов, отвечающих основным реологическим характеристикам (упругость, пластичность, вязкость): идеально упругое тело Гука, идеально вязкое тело Ньютона (ньютоновская жидкость) и идеально пластическое тело Сен-Венана — Кулона. реологии механические свойства материалов представляют в виде реологических моделей, в основе которых лежат три основных идеальных закона, связывающих напряжение с деформацией. Им соответствуют три элементарные модели (элемента) идеализированных материалов, отвечающих основным реологическим характеристикам (упругость, пластичность, вязкость): идеально упругое тело Гука, идеально вязкое тело Ньютона (ньютоновская жидкость) и идеально пластическое тело Сен-Венана — Кулона.
Идеально упругое тело Гука представляют в виде спиральной пружины. В соответствии с законом Гука деформация а упругом теле пропорциональна напряжению сдвига P:
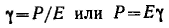
После снятия нагрузки идеально упругое тело Гука мгновенно переходит в первоначальное состояние (форму).
И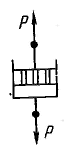 деально вязкое тело Ньютона изображают в виде поршня с отверстиями, помещенного в цилиндр с жидкостью. Идеально вязкая жидкость течет в соответствии с законом Ньютона. Согласно этому закону напряжение сдвига при ламинарном течении жидкости с вязкостью η пропорционально градиенту ее скорости du/dx: деально вязкое тело Ньютона изображают в виде поршня с отверстиями, помещенного в цилиндр с жидкостью. Идеально вязкая жидкость течет в соответствии с законом Ньютона. Согласно этому закону напряжение сдвига при ламинарном течении жидкости с вязкостью η пропорционально градиенту ее скорости du/dx: 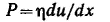
Закон Ньютона можно сформулировать еще следующим образом: напряжение сдвига пропорционально скорости деформации (или скорость деформации пропорциональна напряжению сдвига): 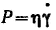
М оделью идеально пластического тела Сен-Венана — Кулона является находящееся на плоскости твердое тело, при движении которого трение постоянно и не зависит от нормальной (перпендикулярной поверхности) силы. В основе этой модели лежит закон внешнего (сухого) трения, в соответствии с которым деформация отсутствует, если напряжение сдвига меньше некоторой величины Рт, называемой пределом текучести, т. е. при оделью идеально пластического тела Сен-Венана — Кулона является находящееся на плоскости твердое тело, при движении которого трение постоянно и не зависит от нормальной (перпендикулярной поверхности) силы. В основе этой модели лежит закон внешнего (сухого) трения, в соответствии с которым деформация отсутствует, если напряжение сдвига меньше некоторой величины Рт, называемой пределом текучести, т. е. при 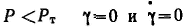 . .
Если напряжение достигнет предела текучести, то развиваемая деформация идеально пластического тела не имеет предела, и течение происходит с любой скоростью, т. е. при 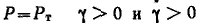 . .
К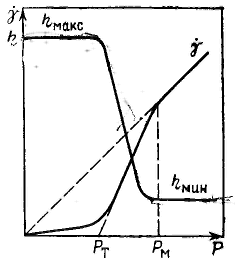 ривые течения структурированных жидкообразных систем могут быть представлены в координатах вязкость — напряжение сдвига. ривые течения структурированных жидкообразных систем могут быть представлены в координатах вязкость — напряжение сдвига.
Из рисунка видно, что свойства структурированных жндкообразных систем могут быть охарактеризованы тремя величинами вязкости: двумя ньютоновскими ηмакс для неразрушенной структуры, ηмин Для предельно разрушенной структуры и пластической вязкостью η* в промежуточной области, моделируемой уравнением Бингама. Наличие структуры и ее прочность, особенно в жидкообразных системах, можно оценивать не только пределом текучести, но и разностью ηмакс — ηмин.
Используя уравнение Гуи-Чепмена, рассчитайте значение потенциала на расстоянии 10 и 30 нм от поверхности (пренебрегая толщиной слоя Гельмгольца). Дисперсионная среда водный раствор ZnCl2 с концентрацией 10-4 моль/л (индифферентный электролит), t = 20 ºС, ε = 80,1; потенциал диффузного слоя 45 мВ.

Экзаменационный билет № 17
Метод избытков Гиббса. Вывод фундаментального адсорбционного уравнения Гиббса. Гиббсовская адсорбция. Частное выражение уравнения Гиббса. Поверхностная активность, поверхностно-активные и поверхностно-инактивные вещества.
Для описания термодинамики поверхностных явлений применяют два метода: метод избыточных величин Гиббса и метод «слоя конечной толщины».
Ч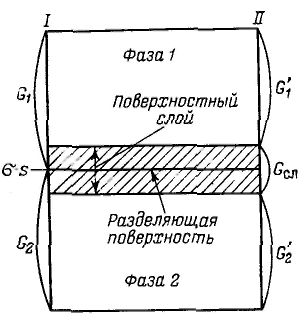 тобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса системы равна сумме энергий Гиббса G1 и G2 объемных фаз 1, 2 и поверхностной энергии Гиббса σs, которая является избыточной: тобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса системы равна сумме энергий Гиббса G1 и G2 объемных фаз 1, 2 и поверхностной энергии Гиббса σs, которая является избыточной: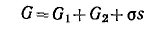
Характеристика величины адсорбции определяющася избытком вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме фазы, также отнесенным к единице площади поверхности или единице массы адсорбента, называется гиббсовской адсорбцией и обозначается буквой гамма Г (метод избыточных величин Гиббса).
Объединенное уравнение первого и второго начал термодинамики для внутренней энергии поверхности с учетом поверхностной и химической энергии имеет вид (объем поверхностного слоя равен нулю)
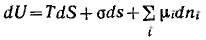 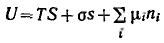
Так как внутренняя энергия поверхности пропорциональна экстенсивным величинам, то
и ее полный дифференциал от тех же переменных запишется следующим образом:
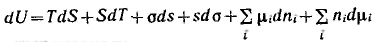 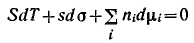
Подставляя значение dU, получим:
Д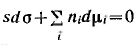 ля условия постоянства температуры это соотношение принимает вид ля условия постоянства температуры это соотношение принимает вид
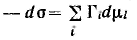
Разделив полученное уравнение на площадь поверхности, получим:
Данное уравнение называют фундаментальным адсорбционным уравнением Гиббса.
Для адсорбции одного конкретного вещества при постоянных химических потенциалах других веществ полученное уравнение можно записать относительно частной производной для данного компонента:
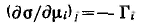
Принимая во внимание, что 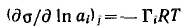
Для гиббсовской адсорбции это выражение принимает вид
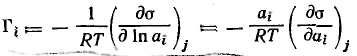
-
Для растворенного вещества это выражение переходит в широко используемые адсорбционные уравнения Гиббса для неэлектролитов
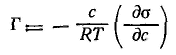
|
и для электролитов при их диссоциации в полярной фазе и отсутствии ее в поверхностном слое (при неполярной второй фазе):
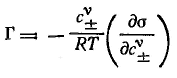
| |
|
|
 Скачать 3.47 Mb.
Скачать 3.47 Mb.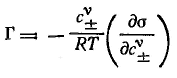

 ависимость скорости коагуляции от концентрации электролита показана на рисунке. Из этого рисунка следует, что введение электролита в дисперсную систему снижает потенциальный барьер, который при быстрой коагуляции (максимальной скорости) становится равным нулю. Порог коагуляции существенно зависит от момента его фиксирования, от метода наблюдения за коагуляцией (изменение интенсивности рассеяния света, реологических свойств и др.) и от концентрации золя, поэтому необходимо всегда подробно указывать условия определения этой величины.
ависимость скорости коагуляции от концентрации электролита показана на рисунке. Из этого рисунка следует, что введение электролита в дисперсную систему снижает потенциальный барьер, который при быстрой коагуляции (максимальной скорости) становится равным нулю. Порог коагуляции существенно зависит от момента его фиксирования, от метода наблюдения за коагуляцией (изменение интенсивности рассеяния света, реологических свойств и др.) и от концентрации золя, поэтому необходимо всегда подробно указывать условия определения этой величины.
 азделим переменные и проведя интегрирование полученного уравнения в пределах от σ0 (поверхностное натяжение чистого растворителя) до σ и соответственно от с = 0 до с. Получим
азделим переменные и проведя интегрирование полученного уравнения в пределах от σ0 (поверхностное натяжение чистого растворителя) до σ и соответственно от с = 0 до с. Получим  озможность существования поверхностных пленок в различных агрегатных состояниях впервые было наглядно показано Ленгмюром. Он специально сконструировал весы для измерения поверхностного (двухмерного) давления. Принцип метода измерения состоит в следующем. В кювету 1 наливают до краев подлежащую жидкость и на ее поверхность между неподвижной 2 и подвижной 3 планками наносят вещество, образующее мономолекулярную пленку. В процессе теплового движения молекулы вещества ударяются о планку и создают давление, которое можно уравновесить и измерить с помощью разновесов в чашечке 4. Передвигая планку 3, можно изменять площадь, занимаемую молекулами пленки, и тем самым изменять ее двухмерное давление.
озможность существования поверхностных пленок в различных агрегатных состояниях впервые было наглядно показано Ленгмюром. Он специально сконструировал весы для измерения поверхностного (двухмерного) давления. Принцип метода измерения состоит в следующем. В кювету 1 наливают до краев подлежащую жидкость и на ее поверхность между неподвижной 2 и подвижной 3 планками наносят вещество, образующее мономолекулярную пленку. В процессе теплового движения молекулы вещества ударяются о планку и создают давление, которое можно уравновесить и измерить с помощью разновесов в чашечке 4. Передвигая планку 3, можно изменять площадь, занимаемую молекулами пленки, и тем самым изменять ее двухмерное давление.
 ривые течения структурированных жидкообразных систем могут быть представлены в координатах вязкость — напряжение сдвига.
ривые течения структурированных жидкообразных систем могут быть представлены в координатах вязкость — напряжение сдвига.
 тобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса системы равна сумме энергий Гиббса G1 и G2 объемных фаз 1, 2 и поверхностной энергии Гиббса σs, которая является избыточной:
тобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса системы равна сумме энергий Гиббса G1 и G2 объемных фаз 1, 2 и поверхностной энергии Гиббса σs, которая является избыточной: