отче по преддипломной. отчёт. Элективный курс Нестандартные уравнения

• Название: Элективный курс Нестандартные уравнения
• Анкор: отче по преддипломной
• Дата: 28.03.2022
• Размер: 0.96 Mb.
• Имя файла: отчёт.docx
• Тип: Элективный курс; #421726

1. 
   Тема выпускной квалификационной работы
   

Элективный курс «Нестандартные уравнения» для профильной подготовки учащихся 11 классов.

2. 
   Актуальность темы исследования
   

Актуальность:

Элективные курсы – это курсы по выбору учащихся, входящие в состав профиля обучения на старшей ступени школы. Они обязательные для посещения.

Главной задачей этих курсов является более глубокое изучение определенной предметной области. Чаще используются для профильной специализации обучения.

В настоящее время в материалах ЕГЭ предлагаются нестандартные уравнения. Незнание таких уравнений существенно уменьшает область успешно решаемых задач. Часто бывают задания, которые можно решить, не используя нестандартные методы, но при этом необходимо производить настолько большое количество различных преобразований и операций, что учащиеся либо получают неправильный ответ, либо теряют интерес к продолжению решения задания. Нестандартные подходы к решению уравнений формируют целостный взгляд на курс математики. Овладение этими способами решения задач позволяет развивать у старшеклассников новое, нешаблонное мышление, которое можно применять также и в других сферах человеческой деятельности.

На обучение нестандартным уравнениям в школьном курсе математики уделяется недостаточно внимания: они либо просто не изучаются, либо изучение происходит в разрыве, не систематизировано. В связи с этим изучение нестандартных уравнений возможно реализовать с помощью элективного курса.

3. 
   Объект исследования
   

Объект исследования – элективные курсы для профильной подготовки школьников.

4. 
   Предмет исследования
   

Предмет исследования-элективный курс «Нестандартные уравнения» для профильной подготовки учащихся 11 классов.

5. 
   Цель исследования
   

Цель исследования – разработка элективного курса по теме: «Нестандартные уравнения» для профильной подготовки учащихся 11 классов, описав основные дидактические аспекты при его изучении, подобрав и систематизировав учебно методические материалы для курса.

6. 
   Задачи исследования
   

задачи:

• 
  изучить и проанализировать нормативные документы, учебно-методическую, психолого-педагогическую литературу относящуюся к элективным курсам и нестандартным уравнениям;
  

• 
  сформировать теоретико-методические представления о школьных элективных курсах;
  

• 
  разработать методическое обеспечение элективного курса «Нестандартные уравнения», включающее в себя: программу, тематическое планирование, содержание курса, подборку заданий и задач, список литературы электива;
  

-рассмотреть современные электронные образовательные ресурсы, их возможности для использования на занятиях элективного курса.

7. 
   Гипотеза исследования
   

Гипотезаисследования заключается в том, что данный элективный курс поможет обеспечить более углубленное изучение одного из разделов математики, устранить расхождения в требованиях по математике, предъявленных к подготовке выпускников в школе и абитуриентов в вузе, расширить возможности развития мыслительной деятельности учащихся.

8. 
   Краткое описание (2страницы) программы, методических рекомендаций или методического обеспечения в соответствии с темой выпускной квалификационной работы исследования (факультативного или элективного курса, цикла занятий по предмету).
   

Краткое описание программы элективного курса «Нестандартные уравнения»

Для того, чтобы познакомить учащихся с интересными нестандартными уравнениями и расширить, углубить знания обучающихся целесообразно включение элективного курса «Нестандартные уравнения»

Решение уравнений вызывают иногда затруднения у обучающихся выпускных классов и на вступительных экзаменах. Учащиеся находятся в боле выигрышной ситуации, да и сама программа предполагает развитие навыков решения заданий сложного уровня. Это связано с тем, что решение таких задач требует не только знания свойств функций и уравнений, умения выполнять алгебраические преобразования, но также высокой логической культуры и хорошей техники исследования.

Данный курс дополняет и углубляет знания, полученные по программе базового уровня. Рассматриваются вопросы, связанные с различными приёмами решения показательных, логарифмических, иррациональных уравнений, а также решение уравнений с использованием свойств входящих в них функций.

Известно, что решение уравнений приводит к систематизации имеющихся знаний, развивает творческое мышление, учит детей к поиску нестандартных ситуаций.

Практическим результатом данного курса является подготовка учащихся к ЕГЭ по математике. Данный элективный курс поможет систематизировать знания по решению уравнений, развить нестандартные способы мышления. В процессе обучения учащиеся овладевают приемами нестандартного подхода к решению уравнений.

Цели курса

систематизировать методы решения уравнений ;

сформировать умения и навыки решения уравнений и неравенств

различными методами;

сравнить известные методы решения с вновь изученными, показать легкость решения с помощью нестандартных методов;

развить познавательный интерес;

развить мыслительные операции (анализ, синтез, сравнение, обобщение и т.д.);

развить самостоятельную умственную активность учащихся; выявление и развитие математических способностей учащихся. формирование основ научного мировоззрения.

Задачи курса

• 
  углубить знания по математике, предусматривающие формирование у обучающихся устойчивого интереса к предмету;
  
• 
  выявить и развить их математические способности;
  
• 
  расширить математические представления учащихся о приёмах и методах решения задач различного типа сложности;
  
• 
  повышение уровня математического и логического мышления учащихся;
  
• 
  развитие навыков исследовательской деятельности;
  
• 
  обеспечить подготовку к поступлению в вуз и продолжению образования;
  
• 
  обеспечить подготовку к профессиональной деятельности, требующей высокой математической культуры.
  

9. 
   Подготовка и публикация статьи(название статьи), участие в конкурсах (название конкурсов)
   

публикация статьи «Решение нестандартных уравнений в школьном курсе математики» в образовательном СМИ «Педагогический альманах» https://www.pedalmanac.ru/129324.

Текст статьи:

Решение нестандартных уравнений в школьном курсе математики.

          Математическое образование в системе основного общего образования занимает одно из ведущих мест. Это определяется, практической значимостью математики, ее возможностями в развитии и формировании мышления человека, ее вкладом в создание представлений о научных методах познания действительности. Изменение приоритетных направлений развития современной системы образования ставит перед школой задачу формирования творчески мыслящих людей, обладающих нестандартным взглядом на проблемы, владеющих навыками исследовательской работы.

 Решение задач - важная часть математического образования. Умение решать задачи является одним из основных показателей уровня математического развития учащихся, глубины усвоения учебного материала.    На уроках математики современной школы характерна репродуктивная деятельность учащихся. Школьники, как правило, решают типовые задачи. Привыкая к выполнению стандартных типовых заданий, имеющих единственное решение, которое заранее предопределено на основе некоторого алгоритма, учащиеся привыкают к однотипным действиям, начинают мыслить по стандарту, практически мало действуют самостоятельно, что не позволяет эффективно развивать собственный интеллектуальный потенциал, прежде всего логическое мышление. Ведь творчество – это умение отказаться от стереотипов мышления, для того чтобы создать что-то новое.

Часто учащиеся сталкиваются с задачами, для которых в курсе математики не имеется общих правил и положений, определяющих точный алгоритм их решения, такие задачи называются нестандартными.[2] Как же решать такие задачи?

Получив задачу необходимо определить к какому классу она относится. Далее необходимо найти план решения. Не нужно представлять себе, что план решения - это точный перечень всех действий, это лишь идея, замысел.

Попробуем определить вид нестандартной задачи. Выделим три вида таких задач по характеру требования:

1. 
   Задачи на нахождение искомого
   
2. 
   Задачи на доказательство или объяснение
   
3. 
   Задачи на преобразование или построение
   

Это очень важный шаг, так как для большинства видов задач  в школьном курсе математики  изучают методы решения. Таким образом, принадлежность задачи к данному виду  дает готовый план её решения.

Если задача осталась не решенной, то необходимо рассмотреть способы приведения данной задачи к ранее решенным. Это значит что мы путем преобразования или переформулирования, а может и с помощью разбиения на стандартные подзадачи, сведем решение данной (незнакомой) задачи к задаче, алгоритм решения которой уже известен.[1]  

В математике нет каких либо общих правил решения нестандартных задач. Но в школьном курсе математики на многих примерах можно показать способы их решения.

Рассмотрим пример.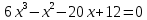

Умножим левую часть уравнения на выражение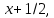



получим: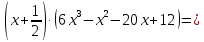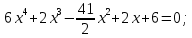





заметим, что при этом действии корень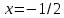



не будет являться корнем исходного уравнения.

Получившееся уравнение является симметрическим уравнением четвертой степени.

Так как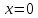



не является корнем исходного уравнения, можно разделить левую часть получившегося уравнения на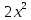



и перегруппировать члены: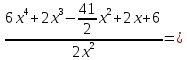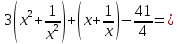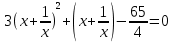







Относительно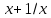



это уравнение решается как квадратное: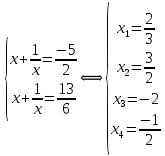



Так как изначально при умножении появился корень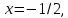



не являющийся корнем исходного уравнения, окончательно получаем ответ: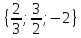



                    

       Большинство учащихся общеобразовательных школ либо вовсе не справляются с такими задачами, либо приводят громоздкие выкладки. Одной из причин этого является отсутствие системы нестандартных задач в школьных учебниках.

Применение нестандартных задач в обучении школьников математике реализуется в разной форме как на уроке: индивидуальные задания, так и во внеклассной работе: кружки, викторины, конкурсы, олимпиады. Но основной организационной формой является урок, где все учащиеся принимают участие в решении нестандартных задач.

При решении нестандартных задач акцент делается не на запоминание фактов, а на умение критически и творчески думать. Школьники сами могут постигать смысл узнаваемого с помощью умения размышлять, задавать вопросы по существу, улавливать взаимосвязи, выявлять модели, принимать правильные решения, понимать и ценить разнообразие алгоритмов решения.   Решение задачи крайне сложный процесс, при описании которого невозможно исчерпать все многообразие его сторон. Дать учащимся правила, позволяющие решить любую нестандартную задачу, невозможно, ибо нестандартные задачи в какой-то степени неповторимы, а универсального метода, позволяющего решить любую задачу, к сожалению, нет. Даже строгое выполнение всех указаний и следование советам учителя не сможет творческий процесс отыскания решений нестандартных задач уложить в определенные схемы.

  Нестандартные задачи служат переходным мостом от классной работы к внеклассной, являются хорошим материалом для выявления наиболее способных к математике учащихся, для дополнительных заданий, как в школе, так и дома.

Последовательное осуществление органической связи между повседневной учебной работой на уроках и внеклассной работой с помощью  нестандартных задач позволит учителю добиться больших успехов в развитии математических способностей отдельных учащихся и всего класса в целом.

ЛИТЕРАТУРА

1. 
   Пойя Ж. Как решать задачу. М.: «Либроком» -208с.
   
2. 
   Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. М.: «Просвещение»,1989.-191с.