шпора тоэ. шпора тоэ 1. Электрическая цепь и её элементы

• Название: Электрическая цепь и её элементы
• Анкор: шпора тоэ
• Дата: 25.03.2022
• Размер: 1.36 Mb.
• Имя файла: шпора тоэ 1.doc
• Тип: Документы; #416361
• страница: 4 из 5

1) Генератор постоянного тока бортовой сети самолета при токе 20 А имеет на зажимах напряжение 200 В, а при токе 60 А – 196 В. Определить внутреннее сопротивление и ЭДС источника электрической энергии.

Основной характеристикой, связывающей напряжение на генераторе и ток нагрузки, является вольтамперная характеристика, называемая внешней характеристикой. Она описывается уравнением U = E - R₀Iи представляет собой прямую линию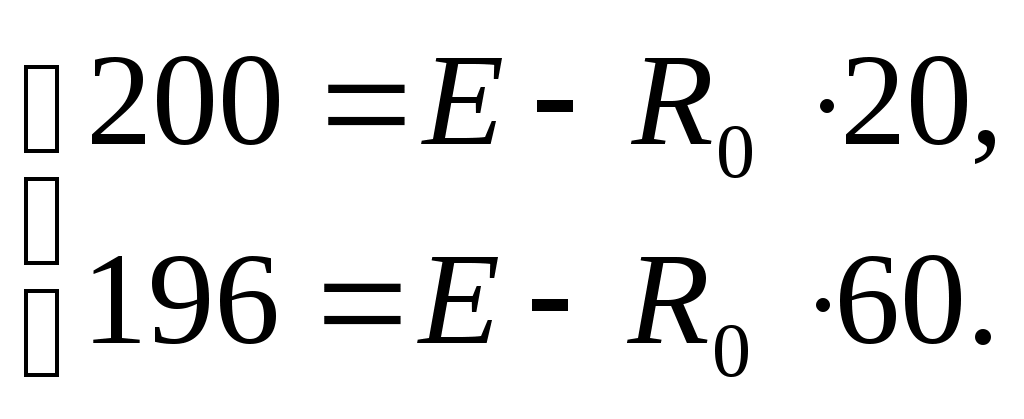



Мгновенная и средняя мощности. Активная, реактивная и полная мощности

Если имеются законы изменения тока и напряжения





то их произведение



Мгновенная мощность

График этой функции - результат графического умножения графиков тока и напряжения.

Под активной мощностью Р понимают среднее значение мгновенной мощности за период Т: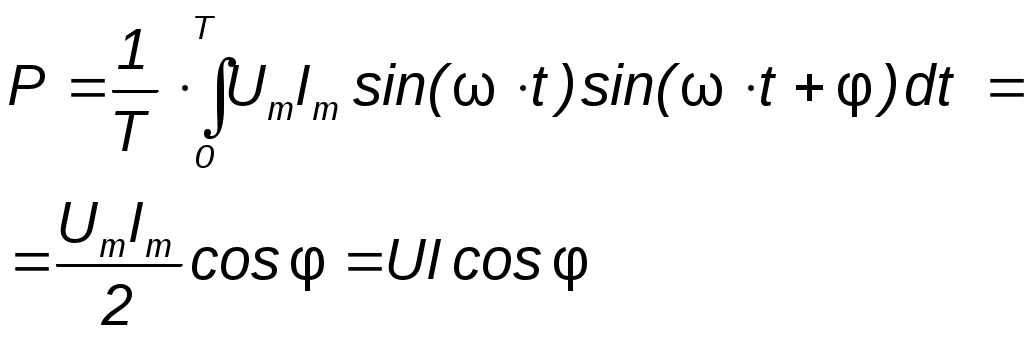

Активная мощность физически представляет собой энергию, которая выделяется в единицу времени в виде теплоты на участке цепи с сопротивлением R. Действительно, произведение . Следовательно:

[Вт]

Под реактивной мощностью Q принимают произведение напряжения на участке цепи на ток, протекающий по этому участку, и на синус угла φ между напряжением и током.


[ ВАр]

Величина, объединяющая активные реактивные мощности, называется полной мощностью.

[ ВА]

Для того, чтобы вычислить полную мощность нужно комплекс напряжения умножить на сопряженный комплекс тока:



Таким образом, активная мощность Р есть действительная часть (Re), а реактивная Q - мнимая часть (Im) произведения


Треугольники сопротивлений, напряжений и мощностей

Полное сопротивления Z



модуль комплексного сопротивления:

строим треуг-к Пифо



Знак угла φ в выражениях для мгновенного значения тока i определяется характером нагрузки: при индуктивном характере нагрузки (X>0) ток отстаёт от напряжения на угол φ и в выражении для мгновенного значения тока угол φ записывают со знаком минус, то есть ; при емкостном характере нагрузки (X<0) ток опережает напряжение на угол φ и выражение мгновенного значения тока записывают со знаком плюс, то есть .
2)

Тоже строим прямоугольный треугольник

Отношение Р к S, равное , называется коэффициентом мощности.



Топографическая и векторная диаграммы

К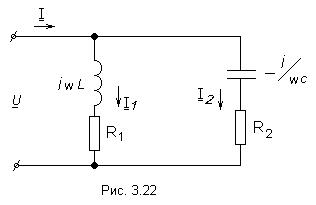
аждая точка электрической схемы, в которой соединяются элементы схемы, имеет своё значение комплексного потенциала.

Совокупность точек комплексной плоскости, изображающих комплексные потенциалы одноимённых точек электрической схемы, называют топографической диаграммой.

Напряжение между любыми двумя точками электрической схемы, например между точками а и в, по значению и направлению определяются вектором, проведённым на векторной диаграмме от точки в к точке а.

Потенциал любой точки схемы может быть принят равным нулю. На диаграмме эту точку помещают в начало координат. Тогда положение остальных точек схемы на диаграмме определяется параметрами цепи, Э.Д.С. и токами ветвей.

Ток и напряжение на различных участках электрической цепи синусоидального тока, как правило, по фазе не совпадают. Наглядное представление о фазовом расположении различных векторов даёт векторная диаграмма токов и напряжений.

Основной функцией векторной диаграммы является качественный контроль аналитических расчетов, который заключается в сравнении этих векторов, исходя из физических соображений. Например, на векторной диаграмме напряжение должно опережать ток на 90⁰, а напряжение отставать от тока на 90⁰.

При несовпадении расчетов с этим положением можно сделать вывод, что в расчете допущена ошибка.
Резонанс напряжений

Условием возникновения резонанса напряжений в последовательном RLC - контуре является равенство реактивных сопротивлений катушки и конденсатора. При значения противоположных по фазе напряжений на индуктивности и на емкости равны, поэтому резонанс в рассматриваемой цепи называют резонансом напряжений.

Полное сопротивление последовательного контура при резонансе минимально и равно активному сопротивлению.



Из формулы закона Ома следует, что при ток в контуре максимален и, ввиду чисто активного сопротивления цепи, совпадает по фазе с приложенным напряжением:

Напряжение на индуктивности и на емкости равны и в Q раз превышают приложенное напряжение:



Величина Q называется добротностью контура и показывает во сколько раз напряжение на реактивном (индуктивном или емкостном) элементе превышает напряжение на входе схемы в резонансном режиме.

где ρ – волновое (характеристическое) сопротивление контура:



Угловая частота, при которой наступает резонанс, называется резонансной угловой частотой:



А частота, при которой возникает резонанс – соответственно резонансной частотой.



Резонанс токов

Рассмотрим цепь с двумя параллельными ветвями

Такую цепь часто называют параллельным контуром. Условием возникновения резонанса является равенство реактивных проводимостей: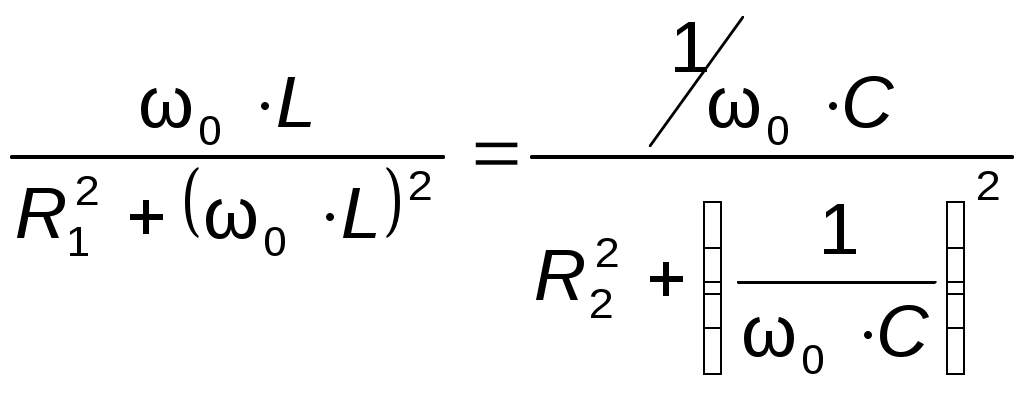





При противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в рассматриваемой цепи получил название резонанса токов.

При резонансе общий ток в параллельном контуре по фазе совпадает с приложенным напряжением.

Добротность контура показывает во сколько раз ток в ветви превышает питающий ток и определяется следующим соотношением:

,где ,

- эквивалентное активное сопротивление при резонансе:

- если

В общем случае резонансная частота 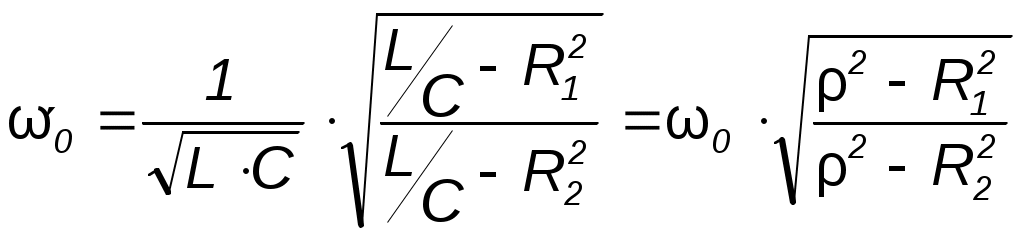определяется по формуле:

где - резонансная угловая частота при - аналогичная последовательному контуру.
Частотные характеристики пассивных двухполюсников

Входное сопротивление и входная проводимость двухполюсника являются функциями частоты ω. Под частотными характеристиками (ЧХ) понимают следующие типы характеристик:

1) Зависимость модуля входного сопротивления (проводимости) от частоты ω.

2) Зависимость действительной или мнимой части входного сопротивления (проводимости) от частоты ω.

ЧХ могут быть получены расчетным (если известна схема, характер элементов и их числовые значения), либо опытным путем (в этом случае схему двухполюсника и характер её элементов знать не обязательно).

При снятии ЧХ опытным путём на вход двухполюсника подают напряжение, частоту которого изменяют в широких пределах, начиная с нуля, и по результатам измерений подсчитывают модуль входного сопротивления (проводимости) или действительную (мнимую) часть входного сопротивления (проводимости).

В общем случае двухполюсники содержат резистивные и реактивные элементы. В частном случае двухполюсники могут состоять из реактивных элементов, тогда их называют реактивными двухполюсниками. Применительно к ним под ЧХ понимают зависимости или . ЧХ для несложных двухполюсников, содержащих резистивные и реактивные элементы, иногда можно качественно строить на основании простых физических изображений о характере изменения сопротивления отдельных элементов этого двухполюсника при изменении частоты. Если это сделать затруднительно, то прибегают к аналитическому расчету, либо к снятию ЧХ опытным путём.

Рассмотрим вопрос о построении ЧХ реактивных двухполюсников, не содержащих резистивных сопротивлений.

Входное сопротивление их , а входная проводимость

Частотная характеристика таких двухполюсников - это зависимость X(W) или b(W). Эти зависимости взаимно обратные.
Индуктивно связанные элементы. Э.Д.С. взаимной индукции

Е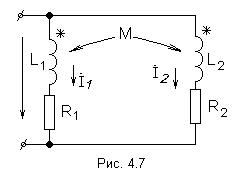
сли изменение тока в одном из элементов электрической цепи приводит к возникновению Э.Д.С. в другом элементе цепи, то говорят, что эти элементы индуктивно связаны друг с другом. Возникающая при этом Э.Д.С. называется Э.Д.С. взаимной индукции.

Н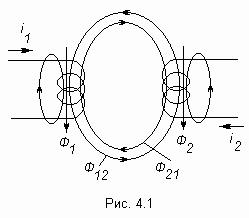
а рис. показаны две катушки с числом витков W(1) и W(2) магнитный поток первой катушки пропорционален протекающему по ней току . Часть этого потока пронизывает витки второй катушки и оказывает влияние на ток .

Аналогично магнитный поток второй катушки пронизывает витки первой.

Такие катушки называются индуктивно – связанными (или магнитно-связанными).

Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи k, который определяется отношением:

=<1

где М - взаимная индуктивность элементов цепи, Гн.

- индуктивности элементов, Гн.

Вообще, взаимной индуктивностью первой и второй катушек называется отношение добавочного потокосцепления второй катушки к току первой катушки:





Индекс 12 показывает, что взаимная индуктивность наводится в первой катушке от действия магнитного потока второй катушки.

Опыт показывает, что:

Взаимная индуктивность в линейных электрических цепях не зависит от направлений и значений токов, и определяется только конструкцией катушек их взаимным расположением. Индуктивность катушки :



П
ри составлении уравнений для магнитно-связанных цепей необходимо знать, согласно или встречно направлены потоки самоиндукции и взаимоиндукции. Правильное заключение об этом можно сделать, если известно направление намотки катушек на сердечнике и выбрано положительное направление токов в них.

П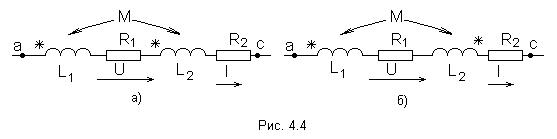
оследол-ное соединение индуктивно связанных элементов цепи

Две катушки с сопротивлениями R₁ и R₂, индуктивностями L₁ и L₂ и взаимной индуктивностью М соединены последовательно. Возможны два вида их включения: согласное (рис. 4.4а) и встречное (рис. 4.4б).

При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов, поэтому магнитные потоки самоиндукции Ф₁₁ (или Ф₂₂) и взаимной индукции Ф₁₂ (или Ф₂₁), сцепленные с каждым элементом, складываются. При встречном включении токи в обоих элементах цепи в любой момент времени направлены противоположно относительно одноименных выводов, поэтому магнитные потоки самоиндукции и взаимной индукции, сцепленные с каждым элементом, вычитаются.

Индуктивность двух последовательно соединенных индуктивно связанных элементов определяется выражением:



где и - потокосцепления первого и второго элементов, причем

Знак плюс относится к согласному, а знак минус ко встречному включению. Следовательно,

L = L₁ + L₂ ± 2M. Полное сопротивление при согласном включении больше, чем при встречном. Напряжения на элементах имеют по три составляющ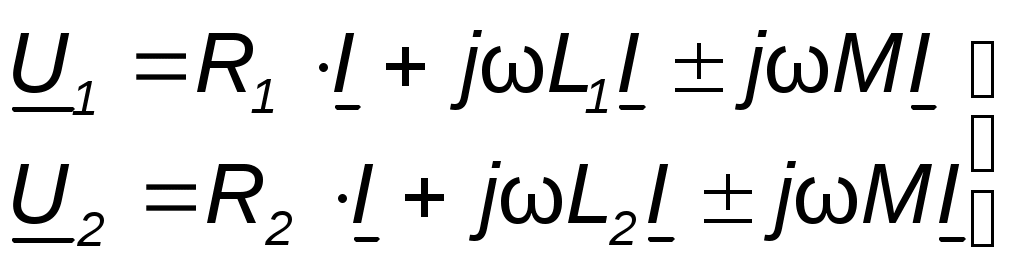