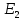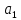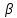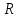ргр 1 схема 5. Записать систему независимых уравнений по законам Кирхгофа для мгновенных значений токов
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
Министерство образования и науки Российской Федерации федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Инженерная школа энергетики Отделение Электроэнергетики и электротехники Линейные электрические цепи с гармоническими напряжениями и токами Вариант 765
Томск – 2018 ЗаданиеЗаписать систему независимых уравнений по законам Кирхгофа для мгновенных значений токов. Рассчитать без учета M комплексные сопротивления ветвей, соединяющих узлы, помеченные на схеме буквами, и изобразить комплексную схему замещения с этими сопротивлениями для расчета комплексов действующих значений токов ветвей (номера и направления токов сохранить согласно заданию № 1, причем параллельное соединение R и С представить в виде одного комплексного сопротивления). Не исключая индуктивной связи, определить комплексы действующих значений токов всех ветвей и напряжение на зажимах источника тока: • по законам Кирхгофа; • методом контурных токов. Записать мгновенные значения тока в ветви ab и напряжения на зажимах источника тока. Рассчитать балансы активной и реактивной мощностей. Построить лучевую диаграмму токов и совмещенную с ней топографическую диаграмму напряжений. Определить показание вольтметра. Сделать развязку индуктивной связи и по методу эквивалентного генератора относительно сопротивления R ветви ab определить комплексное сопротивление активного двухполюсника (эквивалентного генератора) 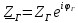 , ЭДС генератора , ЭДС генератора 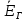 и ток и ток 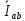 в ветви ab от 0 до в ветви ab от 0 до 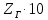 рассчитать и построить зависимость для активной мощности рассчитать и построить зависимость для активной мощности 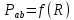 . .Проанализировать результаты вычислений и сформулировать выводы по заданию. ОглавлениеЗадание 2 Линейные электрические цепи с гармоническими напряжениями и токами 4 Система независимых уравнений по законам Кирхгофа для мгновенных значений токов 5 Расчет комплексных значений сопротивления цепи без учета индуктивной связи 6 Определение комплексных значений токов в ветвях и напряжения на зажимах источника тока 7 Мгновенные значения тока в ветви ab и напряжения на зажимах источника тока 9 Баланс мощностей 9 Векторные диаграммы 11 Определение показаний вольтметра 13 Метод эквивалентного генератора 14 Расчет мощности 16 Вывод 17 Линейные электрические цепи с гармоническими напряжениями и токамиДля данной схемы данные значения записаны в таблице 1. 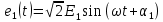 , В; , В; , В; , В;  ,В; ,В; , А. , А.Таблица 1. Заданные значения величин
Изображаем схему 5, данную по варианту. (Рисунок 1).  Рисунок 1. Исследуемая схема Рассмотрим ток в ветви с источником, он находится в ветви с источником тока, поэтому делаем вывод, что ток равен  . Так как . Так как  ,В, то впоследствии его учитывать не будем . ,В, то впоследствии его учитывать не будем .Система независимых уравнений по законам Кирхгофа для мгновенных значений токовЗаписываем систему независимых уравнений по законам Кирхгофа для мгновенных значений токов (функций времени). Для этого указываем номера и направления токов в ветвях схемы и направления обхода контуров (рисунок 2). Учитывая, что  ,В можно объединить узлы kиdа также объединить узлы aи m. Получаем, что в схеме имеет 4 узла и 7 ветвей, это означает, что для разрешения схемы нужно составить 3 первых и 4 вторых уравнения Кирхгофа. ,В можно объединить узлы kиdа также объединить узлы aи m. Получаем, что в схеме имеет 4 узла и 7 ветвей, это означает, что для разрешения схемы нужно составить 3 первых и 4 вторых уравнения Кирхгофа. Рисунок 2. Схема для составления законов Кирхгофа Составим Первые уравнения Кирхгофа для узлов a, b, c. Узел a: 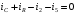 Узел b: 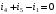 Узел с: 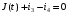 Составим вторые уравнения Кирхгофа для выделенных контуров учитывая то, что на схеме катушки включены согласно. Для контура 1к: 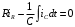 Для контура 2к: 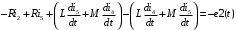 Для контура 3к: 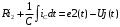 Для контура 4к: 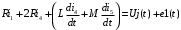 Найти токи из этих дифференциальных уравнений весьма трудоемко. Поэтому используем символический метод, позволяющий дифференциальные уравнения с синусоидальными напряжениями и токами преобразовать к алгебраическим уравнениям с комплексными величинами, решить которые значительно проще. Расчет комплексных значений сопротивления цепи без учета индуктивной связи. Рассчитываем без учета взаимной индуктивности M комплексные сопротивления ветвей, соединяющих узлы a, b, c, d и изображаем комплексную схему замещения с этими сопротивлениями и комплексами действующих значений (Рисунок 3).   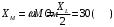 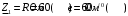 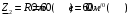 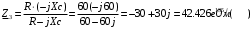 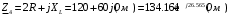 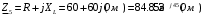 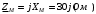  Согласное включение.  Рисунок 3. Преобразованная схема Определение комплексных значений токов в ветвях и напряжения на зажимах источника токаИспользуем законы Кирхгофа в комплексной форме ( 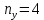 число узлов, число узлов, 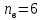 число ветвей, число ветвей, 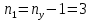 число уравнений по первому закону Кирхгофа, число уравнений по первому закону Кирхгофа,  число уравнений по второму закону Кирхгофа): число уравнений по второму закону Кирхгофа):Составим первые уравнения Кирхгофа для узлов a, b, cсоответственно:  Составим вторые уравнения Кирхгофа для выбранных на рисунке 3 контуров 1к, 2к, 3к соответственно: 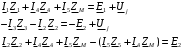 Решаем полученные уравнения матричным методом в Mathcad. Получились следующие значения:  Используем метод контурных токов в комплексной форме ( 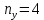 число узлов, число узлов, 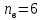 число ветвей, число ветвей,  число неизвестных токов, число неизвестных токов, 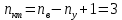 число контурных токов, число контурных токов,  число контурных уравнений). Изобразим контурные токи на рисунке 4. число контурных уравнений). Изобразим контурные токи на рисунке 4.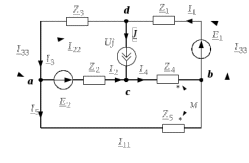 Рисунок 4. Контурные токи Контурные токи направляем так, чтобы через источник тока проходил один контурный ток и через каждое индуктивно связанное сопротивление проходил один свой контурный ток. В результате получим следующие уравнения для контурных токов (встречное включение): 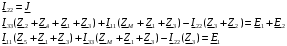 Решаем полученные уравнения матричным методом в Mathcad. Найдем напряжение на зажимах источника тока по второму закону Кирхгофа, выбрав контур обхода 2к (рисунок 3). 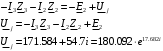 Таким образом, полученные результаты совпали с результатами, найденными при помощи законов Кирхгофа. Мгновенные значения тока в ветви ab и напряжения на зажимах источника тока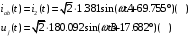 Баланс мощностейПолная вырабатываемая мощность всех источников: 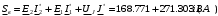 Активная потребляемая мощность:  Причем значения токов – действующие. Реактивная потребляемая мощность:  Погрешность расчетов: Погрешности расчетов. − По активной мощности: 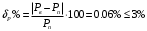 По реактивной мощности: 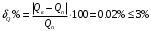 Векторные диаграммыСтроим лучевую векторную диаграмму токов (Рисунок 5) и совмещенную с ней топографическую векторную диаграмму напряжений (Рисунок 6).  Рисунок 5. Лучевая диаграмма токов Для упрощения построения топографической диаграммы напряжений на комплексной схеме расставляем стрелки напряжений навстречу направлениям токов. Далее, используя закон Ома и учитывая наличие индуктивной связи, проводим расчет этих напряжений (согласное включение):  Рассчитываем комплексные потенциалы узлов и точки k схемы (Рисунок 3), предварительно приняв,  : : 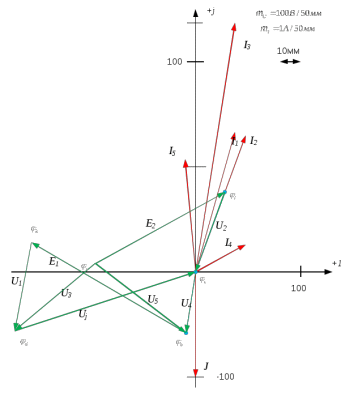 Рисунок 6. Топографическая диаграмма напряжений Определение показаний вольтметраОпределяем показание вольтметра аналитически и графически, как действующее значение напряжения, между точками включения вольтметра, т.е. между узлами c и b(Рисунок 1). − Аналитически: 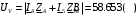 − Графически (по векторной диаграмме):  Метод эквивалентного генератораДелаем развязку индуктивной связи (Рисунок 7) и методом эквивалентного генератора находим ток ветви ab. При развязке учитываем, что индуктивно связанные сопротивления подходят к общему узлу b одинаковым образом. 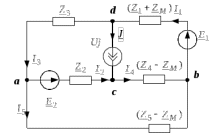 Рисунок 7. Развязка индуктивной связи Для использования метода эквивалентного генератора необходимо найти напряжение холостого хода  ,с помощью метода контурных токов (Рисунок 9), и эквивалентное сопротивление генератора ,с помощью метода контурных токов (Рисунок 9), и эквивалентное сопротивление генератора 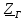 по схеме преобразований (Рисунок 8). по схеме преобразований (Рисунок 8). Рисунок 8. Определение  Определим значение 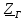 : :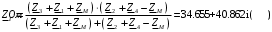 Определим значение  : : Рисунок 9. Нахождение   Найденный ток совпал со значениями, найденными при помощи законов Кирхгофа и метода контурных токов. Расчет мощностиЗатем изменяя величину сопротивления R ветви ab от 0 до 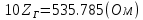 рассчитываем мощность рассчитываем мощность , которая выделяется в виде тепла в этом сопротивлении: , которая выделяется в виде тепла в этом сопротивлении: Результаты расчетов этой мощности вносим в таблицу:
Максимум мощности  наблюдается при условии 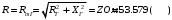 Строим график зависимости  (Рисунок 10) (Рисунок 10)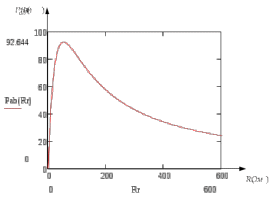 Рисунок 10. Зависимость  ВыводВ ходе работы была исследована электрическая цепь с гармоническими напряжениями и токами и индуктивно связанными элементами. В ходе работы был применен символьный метод для расчета цепи. Были получены значения токов во всех ветвях цепи и напряжение на зажимах источника тока методом законов Кирхгофа и методом контурных токов. Полученные значения сошлись. Были построены векторные диаграммы: лучевая диаграмма для токов и топографическая диаграмма для напряжений. Был использован метод эквивалентного генератора совместно развязкой индуктивной связи и получено значение тока в ветви abкоторое совпало с полученными ранее значениями. Расчетные токи и напряжение на зажимах источника тока были проверены балансом мощностей, с погрешностью меньше 3%. Был произведен расчет мощности, выделяемой в ветви abи установлена зависимость выделяемой мощности от активного сопротивления ветви, причем при условии, что активное сопротивление равно по значению модулю общего сопротивления генератора, то выделяемая мощность максимальна, это же видно и по графику мощности. Сравнивая трудоемкость методов расчета можно сказать, что метод контурных токов удобнее использовать при наличии источников тока, а метод генератора, когда надо найти ток в конкретном узле, причем сопротивление в этом узле может изменяться (иначе это не выгодно). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||