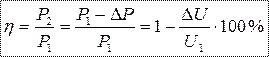ответы на вопроы. Электрическая проводимость в проводнике. Электрическое сопротивление

• Название: Электрическая проводимость в проводнике. Электрическое сопротивление
• Дата: 14.05.2021
• Размер: 0.54 Mb.
• Имя файла: ответы на вопроы.docx
• Тип: Документы; #205076
• страница: 2 из 4

Первый и второй закон Кирхгофа

Законы Кирхгофа для цепи постоянного тока

Первый закон Кирхгофа

В любом узле электрической цепи алгебраическая сумма токов равна нулю

 ,

 

где m – число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус».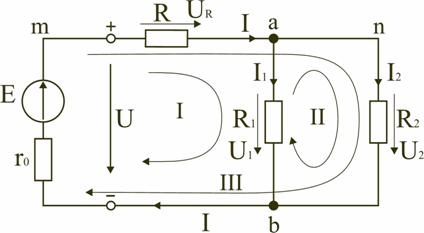



Например, для узла а (см. рис. выше) I−I₁−I₂=0.

Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках.



где n – число источников ЭДС в контуре;

m – число элементов с сопротивлением Rk в контуре;

Uk=RkIk – напряжение или падение напряжения на k-м элементе контура.

Для схемы (рис. выше) запишем уравнение по второму закону Кирхгофа: E=U_R+U₁.

Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контру, включая источники ЭДС равна нулю. 

При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. выше):

контур I: E=RI+R₁I₁+r₀I,

контур II: R₁I₁+R₂I₂=0,

контур III: E=RI+R₂I₂+r₀I.

В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия

W=I²R_t. (1)

Скорость преобразования электрической энергии в другие виды представляет электрическую мощность P=W/t=I²R=UI.

Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.



Это соотношение (1) называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение EI подставляют в (1) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение EI подставляют в (1) со знаком минус. Для цепи, показанной на рис. выше в этой теме уравнение баланса мощностей запишется в виде: EI=I²(r₀+R)+I₁²R₁+I₂²R₂.

При расчете электрических цепей используются определенные единицы измерения. Электрический ток измеряется в амперах (А), напряжение – в вольтах (В), сопротивление – в омах (Ом), мощность – в ваттах (Вт), электрическая энергия – ватт-час (Вт-час) и проводимость – в сименсах (См).

Кроме основных единиц используют более мелкие и более крупные единицы измерения: миллиампер (1 мA = 10^–3 А), килоампер (1 кA = 10³ А), милливольт (1 мВ = 10^–3 В), киловольт (1 кВ = 10³ В), килоом (1 кОм = 10³ Ом), мегаом (1 МОм = 10⁶ Ом), киловатт (1 кВт = 10³ Вт), киловатт-час (1 кВт-час = 10³ ватт-час).

6. 
   Последовательное и параллельное соединение пассивных элементов и источников ЭДС
   

Пусть батарею образуют n последовательно соединенных элементов. Батарея замкнута на внешнее сопротивление R (рис. 3.7). Сопротивлением соединительных проводов пренебрегаем.Запишем для всего замкнутого контура, образующего цепь, второе правило Кирхгофа. Оно имеет вид:

.

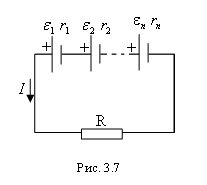
Отсюда

.

В общем случае при последовательном соединении нескольких источников с различными ЭДС сила тока определяется отношением суммы ЭДС всех источников тока к полному сопротивлению всей цепи:

,

где   – внутреннее сопротивление i-го источника, R – сопротивление нагрузки.

Последовательное соединение источников эквивалентно источнику тока с большой ЭДС, однако при этом возрастает его внутреннее сопротивление. Чтобы такое соединение привело к увеличению тока в нагрузке по сравнению с током от одного источника, необходимо, чтобы  . При этом  .

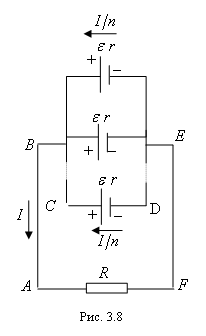
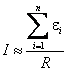Рассмотрим параллельное соединение в батарею n одинаковых элементов с ЭДС   и внутренним сопротивлением r (рис. 3.8). Пусть батарея замкнута на внешнее сопротивление R. Сопротивлением соединительных проводов пренебрегаем. Согласно первому правилу Кирхгофа сила тока   в неразветвленной части цепи равна сумме сил токов во всех элементах батареи. Поэтому через каждый из элементов в отдельности протекает ток силой  . Применим второе правило Кирхгофа к замкнутому участку цепи ABCDEF. Тогда получим  . Отсюда  . Таким образом, при параллельном соединении n одинаковых элементов в батарею ЭДС не меняется, а внутреннее сопротивление уменьшается в n раз. Легко видеть, что параллельное соединение элементов выгодно при малом внешнем сопротивлении. Действительно, если  , то им можно пренебречь, и формула приближенно принимает вид  , то есть сила тока возрастает в n раз по сравнению с силой тока от одного элемента.

7. 
   Потенциальная диаграмма, принцип ее построения
   

р Потенциальной диаграммой замкнутого контура называется графическая интерпретация распределения электронного потенциала вдоль замкнутого контура в зависимости от входящих в него сопротивлений.

Потребитель энергии отображается на электрической схеме как резистор с заданным сопротивлением R. Если такое элемент присутствует в участке цепи, то изменение потенциалов на концах участка будет соответствовать падению напряжения на этом резисторе.

Если на участке цепи присутствует источник напряжения, то на концах такого участка также будет наблюдаться разность потенциалов, численно равная ЭДС источника.

Построение потенциальной диаграммы

Для построения потенциальной диаграммы, замкнутый контур разбивается на участки таким образом, чтобы каждый из них содержал только одного потребителя или один источник электроэнергии.

Потенциальная диаграмма строится в декартовой системе координат, где по оси абсцисс откладывается, с соблюдением масштаба, сопротивление участков цепи, а по оси ординат – потенциалы точек. Точки замкнутого контура и сопротивления элементов откладываются (отмечаются на диаграмме) в той последовательности, в которой они встречаются при обходе контура.

В начало координат диаграммы помещается точка, потенциал которой условно выбран нулевым.

Демонстрацию алгоритма и правил построения потенциальной диаграммы выполним на примере замкнутого контура abcdef (точки a и f совпадают), представленного на рисунке 1. Положительное направление обхода контура – по часовой стрелке. Для расчетов примем:

• 
  Е₁ = 2 В, Е₂ = 3 В;
  
• 
  R₁ = 1 Ом, R₂ = 1 Ом, R₃ = 2 Ом;
  
• 
  I₁ = 1 А, I₂ = 2 А, I₃ = 1 А.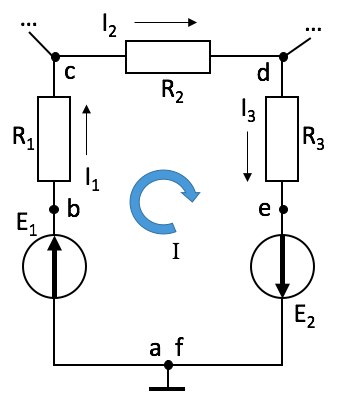
  

Рис. 1. Схема фрагмента электрической цепи — замкнутого контура

Замкнутый контур разбит на участки, каждый из которых содержит либо источник ЭДС, либо резистор.

Примем нулевым потенциал точки а



Следующая точка согласно выбранному направлению движения – b. На участке ab находится источник ЭДС E₁. Так как движение на данном участке происходит от отрицательного полюса источника к положительному (направление обхода контура совпадает со стрелкой источника ЭДС), то значение потенциалы на участке повысится на величину E₁:



Следующий рассматриваемый участок – bc. На нем происходит уменьшение потенциала на величину падения напряжения на резисторе R1.



Аналогичные процессы происходят на участках cd и de. Следовательно,





На участке ef находится еще один источник ЭДС E₂. Движение по данному участку реализуется от отрицательного полюса к положительному, следовательно потенциал повысится на величину E₂



Если направление обхода контура не совпадает с направлением ЭДС, тогда ЭДС записывают со знаком минус 

Значения потенциалов в точках а и f совпадают , что подтверждает правильность расчетов.



На основании полученных данных можно построить потенциальную диаграмму (рисунок 2).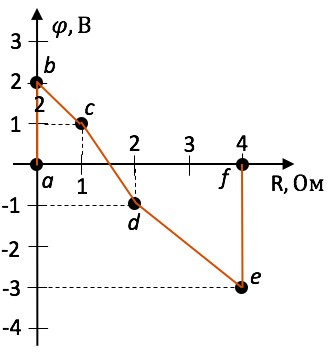

Рис. 2. Потенциальная диаграмма

По потенциальной диаграмме легко можно найти разность потенциалов между любыми точками электрической цепи.

8. 
   Потеря напряжение в проводах
   

при передаче электрической энергии по коротким проводам сопротивлением их можно пренебречь. При большей длине их (l > 10 м) сопротивлением проводов пренебрегать нельзя, так как прохождение тока вызовет в них заметное падение напряжения:



Разность напряжений в начале и конце линии (рис. 2-5) U₁ — U₂, равная падению напряжения в проводах, называется потерей напряжения.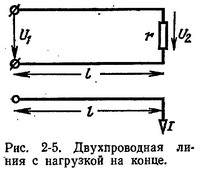





При неизменном напряжении в начале линии напряжение в конце линии, т. е. на приемнике, изменяется от U₂ = U₁ при I = 0 до U₂ = U₁ — ΔU при нагрузке.
Колебание напряжения для осветительной нагрузки не должно превышать — 2,5, +5%, а для силовой ±5 и иногда + 10% номинального. Поэтому допускаемая потеря напряжения в линии не должна превышать тех же значений.
При заданной допустимой потере напряжения, используя формулу (2-31), можно определить необходимое сечение проводов линии



Найденное по формуле (2-33) сечение должно быть проверено на допустимое нагревание.

Мощность потерь в линии определяется произведением потери напряжения и тока, т. е.



Коэффициент полезного действия линии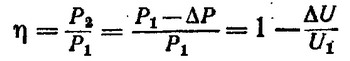



с увеличением нагрузки уменьшается.
При потерях напряжения 2—5% к. п. д. линии составляет 98—95%.

При передаче электрической энергии по коротким проводам сопротивлением их можно пренебречь. При большой длине их (L>10 М) сопротивлениемпроводов пренебрегать нельзя, так как электрический ток вызовет в них заметное падение напряжение.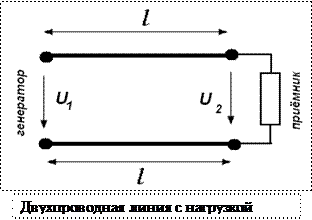

Разность напряжений в начале и в конце линии равна

падению напряжению в проводах и называется

потерей напряжения ΔU .



 





При неизменном напряжении в начале линии

напряжение в конце линии, т. е. на приёмнике,

изменяется.

Чтобы линия была экономичной, необходимо выбирать сечение проводов S в зависимости от:

I – тока - определяется потребителем (приемником энергии);

ρ - удельного сопротивления материала жилы: медь или алюминий;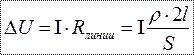

l – длины линии, определяется удалённостью потребителя от источника тока.

Взаимосвязь параметров определяется формулой:

 

При заданной допустимой потери напряжения определяют необходимо сечение проводов линии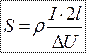

по формуле:

 

Найденное по формуле сечение, округляют до ближайшего большего стандартного. Это сечение должно быть проверено на допустимое нагревание проводов.

При передаче электроэнергии нужно выбрать так сечение проводов линии передачи, чтобы обеспечить нормальное рабочее напряжение U_ном (номинальное напряжение) на зажимах приемников электроэнергии. В особенности это важно для осветительных установок, так как при повышении напряжения только на 5% по отношению к номинальному, длительность горения нормальной лампы уменьшается на 50%; при понижении напряжения на те же 5% световой поток этой лампы уменьшается на 18%.

 

Согласно ПУЭ (Правилам устройства электроустановок):

– на зажимах приборов рабочего освещения производственных помещений и общественных зданий, а так же в прожекторных установках наружного освещения допускается отклонения напряжения (потеря напряжения):

ΔU, % ≤ 2,5% Uн

- на зажимах электродвигателей:

ΔU, % ≤ 5% Uн





Мощность потерь в линии электропередач (ЛЭП) определяется






Коэффициент полезного действия линии (КПД)

с увеличением нагрузки уменьшается

Основным метод снижения потерь напряжения – увеличение напряжения ЛЭП.

В нашей стране существует стандартная шкала переменных напряжений, при которых производится передача энергии на дальние расстояния: 110, 220, 330, 500, 750, 1150 кВ. Например – при повышении напряжения в два раза, если сохранить процент потерь мощности неизменным, можно или уменьшить сечение проводов линии в четыре раза или удлинить линию электропередач в четыре раза.