ответы на вопроы. Электрическая проводимость в проводнике. Электрическое сопротивление

• Название: Электрическая проводимость в проводнике. Электрическое сопротивление
• Дата: 14.05.2021
• Размер: 0.54 Mb.
• Имя файла: ответы на вопроы.docx
• Тип: Документы; #205076
• страница: 3 из 4

Расчет электрических цепей методом свертывания

В соответствии с методом свертывания, отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению, включенному к зажимам источника. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним, эквивалентным по сопротивлению. Определяют ток в упрощенной схеме, затем возвращаются к исходной схеме и определяют в ней токи.
Рассмотрим схему на рис. 3.1. Пусть известны величины сопротивлений R1, R2, R3, R4, R5, R6, ЭДС Е. Необходимо определить токи в ветвях схемы. .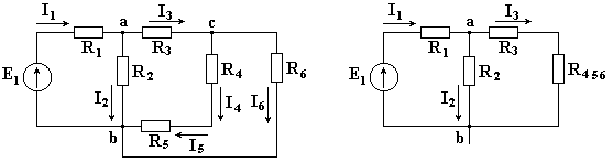


Рис. 3.1 Рис. 3.2 Сопротивления R4 и R5 соединены последовательно, а сопротивление R6 - параллельно с ними, поэтому их эквивалентное сопротивление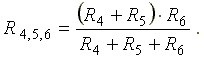



      После проведенных преобразований схема принимает вид, показанный на рис. 3.2, а эквивалентное сопротивление всей цепи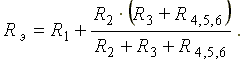



Ток I1 в неразветвленной части схемы определяется по формуле: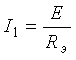



     Найдем токи I2 и I3 в схеме на рис. 3.2 по формулам: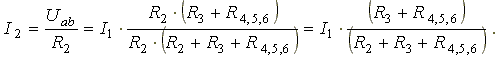



  I3 = I1 - I2 - формула получается из уравнения, составленного по первому закону Кирхгофа:

I₁ - I₂ - I₃ = 0.

    Переходим к исходной схеме на рис. 3.1 и определим токи в ней по формулам: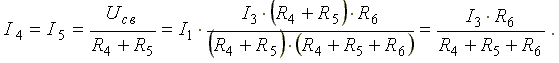



        I6 = I3 - I4 (в соответствии с первым законом Кирхгофа I3 - I4 - I6 =0).

10. 
    Метод преобразования «треугольника» сопротивлений в эквивалентную «звезду»
    

Пусть требуется рассчитать цепь, показанную на рис. 7.1, а.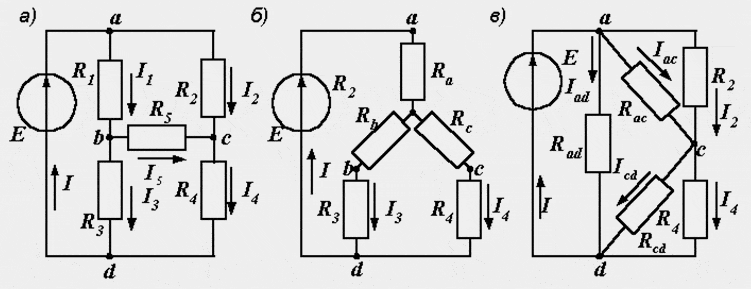



Рис. 7.1 - Преобразования электрической цепи

Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.

Треугольник и звезда сопротивлений имеют вид, показанный на рис. 7.2.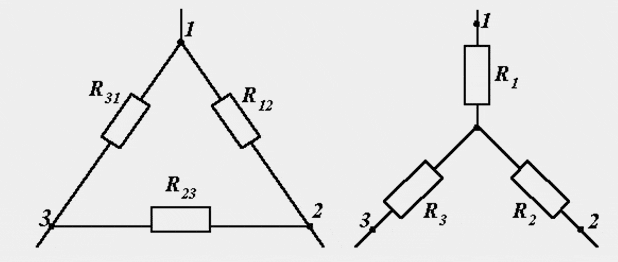



Рис. 7.2 - Треугольник и звезда сопротивлений

Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.

Можно показать, что условием эквивалентности являются следующие уравнения:

а) при преобразовании треугольника в звезду:



б) при преобразовании звузды в треугольник: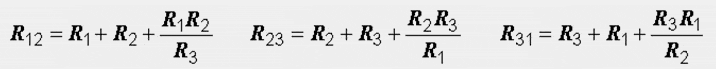



Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.

При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R3.

Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.

а) Решение преобразованием треугольника в звезду.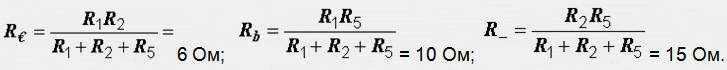



Теперь общее сопротивление цепи легко находится: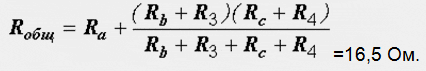



Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен: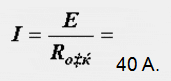



Токи в паралельных ветвях: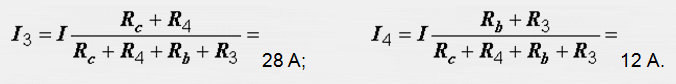



Возвращаемся к исходной схеме (рис. 7.1, а):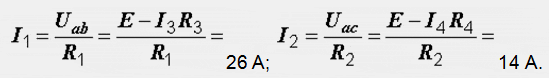



Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A. Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.

б) Решение преобразованием звезды в треугольник.

Преобразуем звезду, образуемую в схеме на рис. 7.1, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 7.1, в).

Определяем сопротивления треугольника: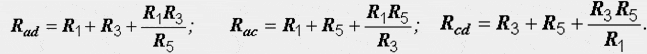



Теперь рассчитываем преобразованную цепь. Сначала находим эквивалентные сопротивления участков ac и cd: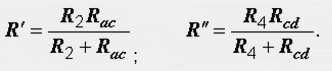



Затем определяем общее сопротивление и токи: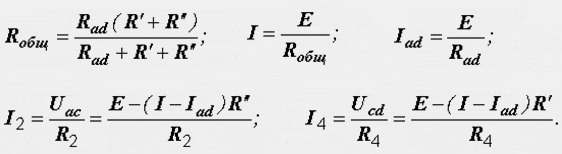



Возвращаемся к исходной схеме:



Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.

11. 
    Метод преобразования «звезды» сопротивлений в эквивалентную «треугольника»
    

На рис. 6.10, а дана электрическая цепь с одним источником питания, широко применяемая в области электрических измере­ний. Особенностью этой цепи является наличие в ней соединений, называемых треугольником и звездой. Треугольником сопротив­лений называют соединение трех ветвей, образующих замкнутый контур с тремя узлами. В схеме рис. 6.10, а имеется два треуголь­ника c сопротивлениями 

Звездой сопротивлений называют соединение трех ветвей, имеющих общий узел. На рис. 6.10, а звезду сопротивлений обра­зуют ветви с сопротивлениями 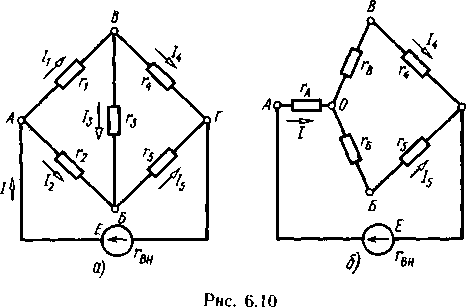  . Любой тре­угольник сопротивлений можно заменить эквивалентной звездой. В результате замены получается другая схема, позволяющая упростить расчет. Например, схема рис. 6.10, а после замены треугольника сопротивлений    эквивалентной звездой    в упрощается (рис. 6.10, б) и содержит только последовательно и параллельно соединенные участки.



 

Эквивалентность треугольника и звезды сопротивлений за­ключается в том, что их замена не изменяет потенциалов узловых точек (на схеме рис. 6.10, а точек А, Б, В), являющихся вершинами треугольника и эквивалентной звезды. Не изменяются также токи, напряжения и мощности в остальной части схемы, не затронутой преобразованием. Для перехода от треугольника соп­ротивлений к эквивалентной звезде пользуются следующими фор­мулами:

 ;   ;   (6.11)

.

Сопротивление 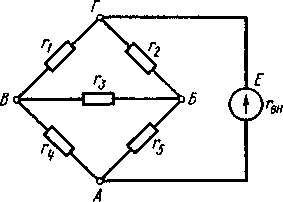   луча А равно произведению двух сопротив­лений треугольника, сходящихся в узле A, деленному на сумму всех сопротивлений треугольника. Так же определяются сопротивления    и   . Вернемся к схе­ме рис. 6.10,6. Ее легко рассчи­тать и определить токи I, I₄ и I₅, которые не изменились после замены треугольника эквивалент­ной звездой. Остальные токи I₁, I₂ и I₃Находят из уравнений по законам Кирхгофа, составленных для исходной электрической схе­мы цепи (рис. 6.10,а).



В некоторых электрических цепях расчет упрощается после замены трехлучевой звезды сопротивлений эквивалентным треугольником. При преобразовании звезды в эквивалентный треугольник пользуются следующими формулами:

 





 



 

 

Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивления двух лучей звезды, присоединенных к те же вершинам, что и сторона треугольника,и их произведения, деленного на сопротивление третьего луча звезды.

 

 

Четырехполюсники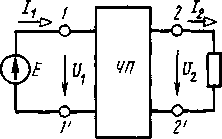



Основные уравнения четырехполюсника. Четырехполюсни­ком называют электрическую цепь, имеющую два входных и два выходных зажима. К входным зажимам 1—1' присоединяется ис­точник электрической энергии, а к выходным 2—2' — приемник с сопротивлением r_н (рис. 6.12). Таким образом, четырехполюсник является промежуточным звеном между источником энергии и ее приемником. К четырехполюсникам можно отнести линии передачи энергии и сигналов, несущих информацию, трансформаторы, рель­совые цепи, фильтры, предназначенные для разделения сигналов, и другие электрические устройства. Внутренняя электрическая схема четырехполюсников может быть весьма сложной и содер­жать ветви с источником энергии. Четырехполюсники с источника­ми энергии называют активными, а без источников — пассивными.

12. 
    Расчет электрических цепей методом узловых и контурных уравнений
    

Метод узловых и контурных уравнений применяется для расчета сложных цепей. Для определения токов в цепи необходимо составить систему уравнений, применив два закона Кирхгофа. Количество уравнений в системе должно быть равно числу неизвестных токов.

Порядок выполнения расчета

• 
  1. Определяют число неизвестных токов (сколько ветвей — столько и токов).
  
• 
  2. Произвольно выбирают направление токов и обозначают их на схеме.
  
• 
  3. Составляют уравнения по первому закону Кирхгофа, число которых на единицу меньше, чем число узлов в схеме.
  
• 
  4. Составляют недостающие до общего числа уравнения по второму закону Кирхгофа. Направления обхода контуров рекомендуется выбирать одинаковыми.
  
• 
  5. Определяют неизвестные токи, решая полученную систему уравнений. Если найденный ток имеет отрицательную величину, то это означает, что его направление противоположно выбранному в п. 2.
  
• 
  6. Проводят проверку, составляя баланс мощностей или рассчитывая цепь другим методом.
  

Для цепи (рис. 3.39) составим систему уравнений по методу узловых и контурных уравнений. Цепь имеет пять ветвей, следовательно, пять токов, т.е. необходимо составить пять уравнений, из них два уравнения по первому закону Кирхгофа (в цепи три узла) и три уравнения по второму закону Кирхгофа: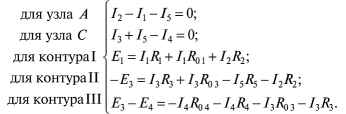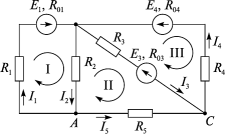

 

Рис. 3.39

Расчет токов разберем на конкретном примере.

Пример 3.13

Определить токи в цепи (рис. 3.40), имеющей следующие параметры: Е = 60 В; ?₂ = 48 В; Е₃ = 6 В; Д = 200 Ом; /?₂ = 100 Ом; R₃ = 10 Ом, методом узловых и контурных уравнений.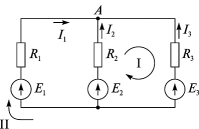



Рис. 3.40

Решение

В цепи три ветви, следовательно, произвольно выберем направление трех токов и составим систему из трех уравнений по законам Кирхгофа: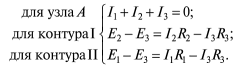 

Решим полученную систему уравнений, подставив заданные числовые значения: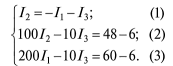



Подставим уравнение (2) в уравнение (1)



Умножим уравнение (4) на 2



Проведем сложение уравнений (3) и (5)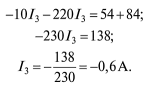



Подставим значение тока /₃ в уравнение (4)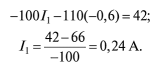



Подставим значение токов 1_{ и /₃ в уравнение (1)



Правильность полученного результата проверим, рассчитав эту же цепь другим методом (методом контурных токов, который будет рассмотрен далее).

13. 
    Расчет электрических цепей методом наложение токов
    

По методу наложения рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя остальные ЭДС из схемы, но оставляя в схеме внутренние сопротивления источников. Затем находят токи в ветвях исходной схемы путем алгебраического сложения частичных токов.

Порядок выполнения расчета рассмотрим на примере схемы, показанной на рис. 6, а.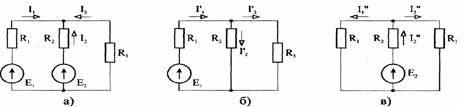

1. 
   Определяют частичные токи I₁‘, I₂‘ и I₃‘ в ветвях электрической цепи при действии одной ЭДС E₁ (ЭДС Е₂ исключена из цепи) (рис. 6, б).
   Направление частичных токов задают в соответствии с направлением ЭДС, расчет токов ведут с использованием метода эквивалентных преобразований.
   
2. 
   Определяют частичные токи I₁«, I₂» и I₃» при действии ЭДС Е₂ (рис.6, в). (ЭДС E₁ исключена из цепи).
   
3. 
   Определяют реальные токи I₁, I₂ и I₃ в ветвях исходной цепи (рис.6, а) как алгебраическую сумму частичных токов при мысленном совмещении цепей, изображенных на рис. 6, б и 6, в.
   

Частичный ток берется со знаком «плюс», если его направление совпадает с направлением реального тока в исходной цепи, со знаком «минус» — при встречном направлении.