Электрический взрыв проводника. НИР_Зинчук_Е.Д._Электрический взрыв проводника_гр.Д-238п_отчет. электрический взрыв проводника

• Название: электрический взрыв проводника
• Анкор: Электрический взрыв проводника
• Дата: 31.10.2021
• Размер: 1.82 Mb.
• Имя файла: НИР_Зинчук_Е.Д._Электрический взрыв проводника_гр.Д-238п_отчет.docx
• Тип: Документы; #259898
• страница: 3 из 9

2 Теории и феноменология электрического взрыва проводника

Электрический взрыв проводников (ЭВП) — явление, известное уже более двухсот лет. Несмотря на столь долгую историю интерес к этому явлению не утрачен до сих пор, наоборот, в последние годы он значительно вырос. С одной стороны, это связано с привлекательностью ЭВП как объекта фундаментальных исследований, поскольку в веществе взрывающейся проволочки термодинамические параметры (температура и плотность) достигают экстремальных значений; с другой стороны, взрывающиеся проволочки широко используются в различных технических приложениях. Технологическое применение ЭВП нашел в 1940–1950- х гг., когда взрыв проводников стал использоваться в ракетной технике при поджоге ракетного топлива. Другие технологические применения ЭВП — это обострение электрической мощности в высоковольтной импульсной технике; получение нанопорошков; создание рентгеновских источников для микроэлектроники и т. п. В последние годы рост интереса к исследованию ЭВП связан с успешными экспериментами по получению мягкого рентгеновского излучения при сжигании многопроволочных цилиндрических оболочек на установке Ангара-5- и на генераторе Z, Сандия, США. В этих экспериментах взрыв проволочек является начальной фазой сжатия плазменных лайнеров, а в финале имплозии возникает высокотемпературная плотная плазма, которая служит мощным источником мягкого рентгеновского излучения (рекордные выходы излучения — около 2 MJ за импульс), перспективного с точки зрения УТС. Сам взрыв проводников сопровождается формированием плотной неидеальной плазмы, а характеристики взрыва служат важным источником информации о транспортных и теплофизических свойствах неидеальной плазмы. С этой точки зрения наибольший интерес представляет ЭВП не в вакууме, где проявляются такие явления, как стратообразование, десорбция газа с поверхности металла и т. д., которые напрямую не связаны с транспортными свойствами проводника, а в жидком диэлектрике, в частности, в воде. Целью данной работы является исследование влияния давления окружающей среды на характеристики взрыва проводников в жидком диэлектрике. В качестве жидкого диэлектрика использовалась дистиллированная вода. Высокое давление в среде жидкого диэлектрика, окружающего исследуемый проводник, создавалось с помощью формирования сходящейся цилиндрической ударной волны. Исследуемым объектом являлся вольфрамовый микропроводник диаметром 30 µm. Эксперименты проводились в два этапа, на первом изучались параметры сходящейся цилиндрической ударной волны, образованной взрывом в воде многопроволочного каскада. Определялось время прихода ударной волны на ось системы, а по скорости распространения данной ударной волны оценивалось давление за ее фронтом. На втором этапе проводились эксперименты по взрыву вольфрамового микропроводника в зоне высокого давления. Вольфрамовый проводник располагался по оси каскада, а его взрыв осуществлялся в момент прихода ударной волны на ось системы. Параллельно с экспериментами проводилось магнитогидродинамическое моделирование процесса взрыва.

3 Физические модели электрического взрыва проводника

3.1 Магнитогидродинамическая модель

Моделирование процесса электрического взрыва проводников проводилось в рамках однотемпературного магнитогидродинамического приближения. В случае цилиндрической геометрии МГД уравнения имеют вид: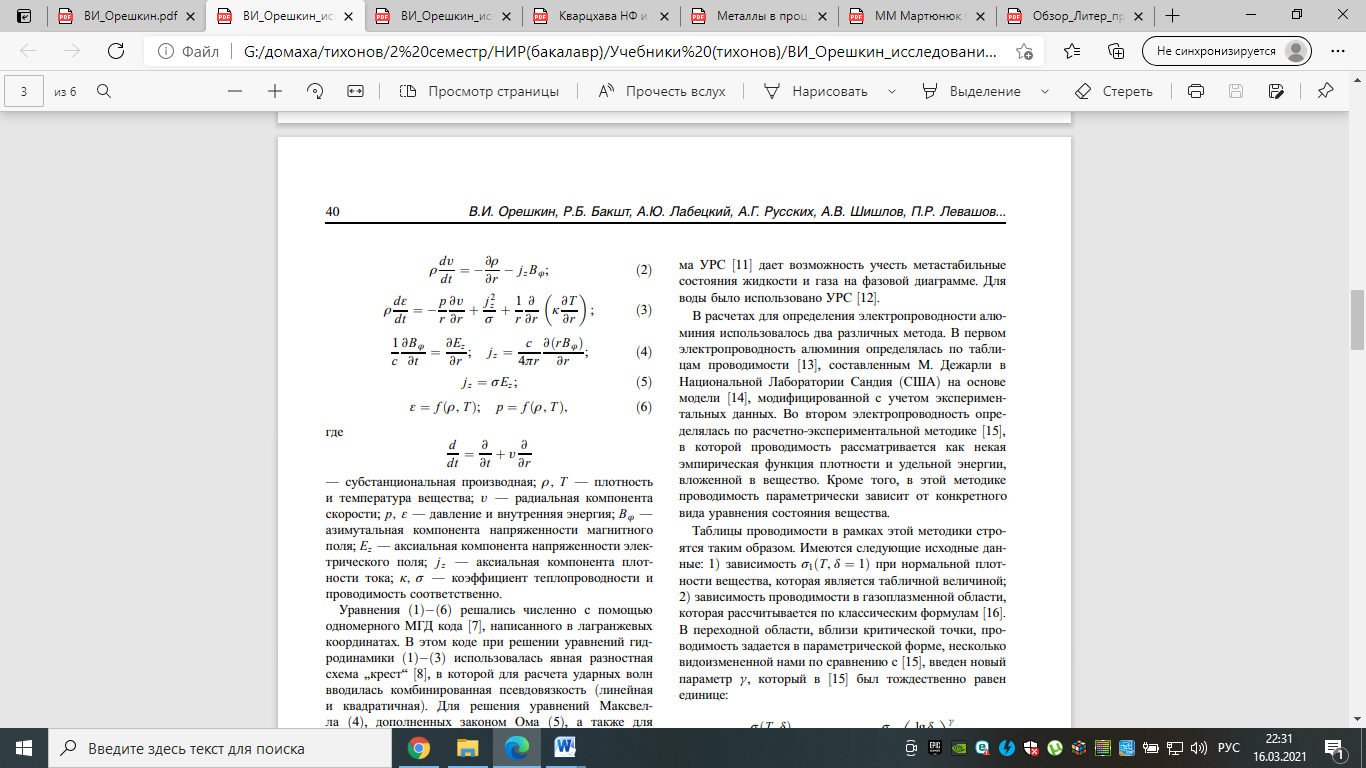





где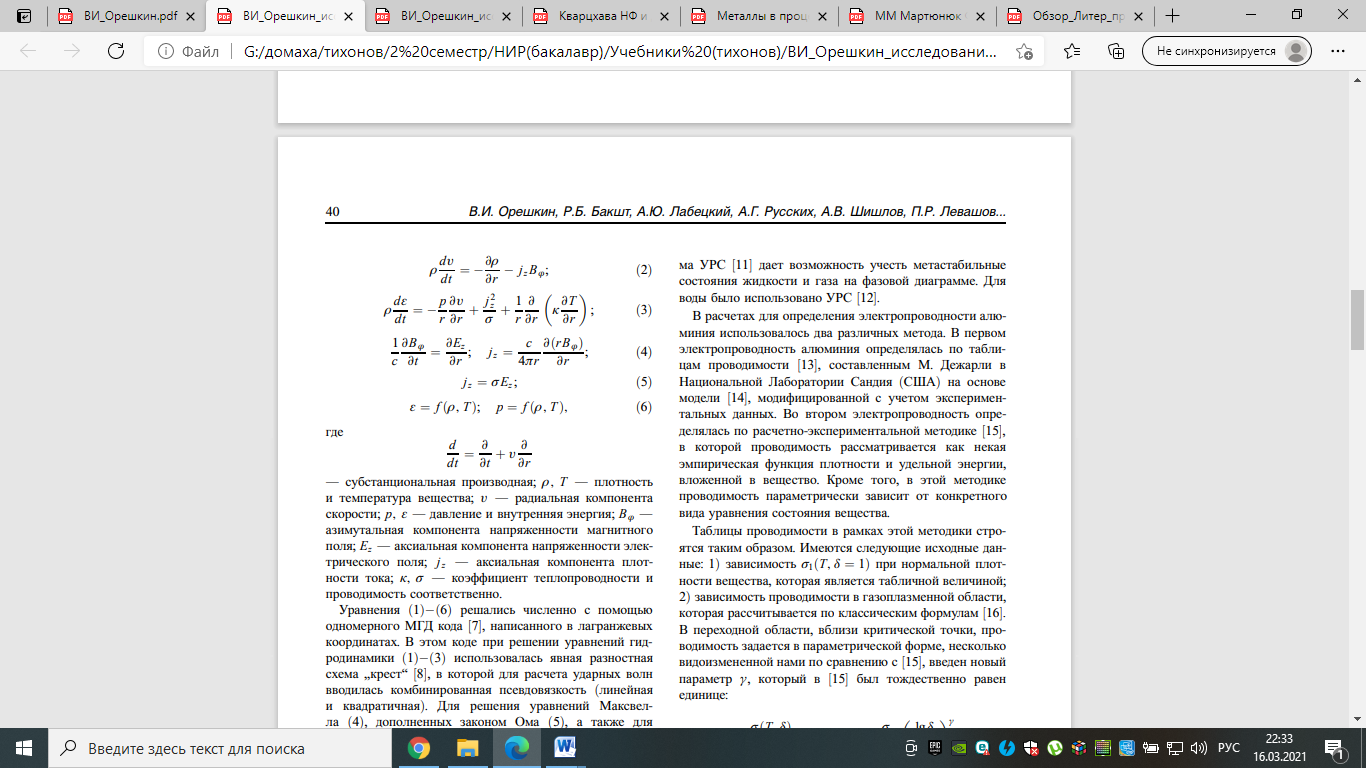


— субстанциональная производная; ρ, T — плотность и температура вещества; v — радиальная компонента скорости; p, ε — давление и внутренняя энергия; Bϕ — азимутальная компонента напряженности магнитного поля; Ez — аксиальная компонента напряженности электрического поля; jz — аксиальная компонента плотности тока; κ, σ — коэффициент теплопроводности и проводимость соответственно. Уравнения (1)−(6) решались численно с помощью одномерного МГД кода, написанного в лагранжевых координатах. В этом коде при решении уравнений гидродинамики (1)−(3) использовалась явная разностная схема „крест“ , в которой для расчета ударных волн вводилась комбинированная псевдовязкость (линейная и квадратичная). Для решения уравнений Максвелла (4), дополненных законом Ома (5), а также для решения уравнения теплопроводности использовались неявные разностные схемы, основанные на методе потоковой прогонки. При численном моделировании взрыва электрических проводников в воде расчетная сетка состояла из двух областей: вещество проводника и вода. Предполагалось, что проводимость воды равна нулю, поэтому весь ток протекает по металлу, а в воде рассматривается лишь прохождение ударной волны. Граничное условие, накладываемое на уравнения Максвелла, имело вид: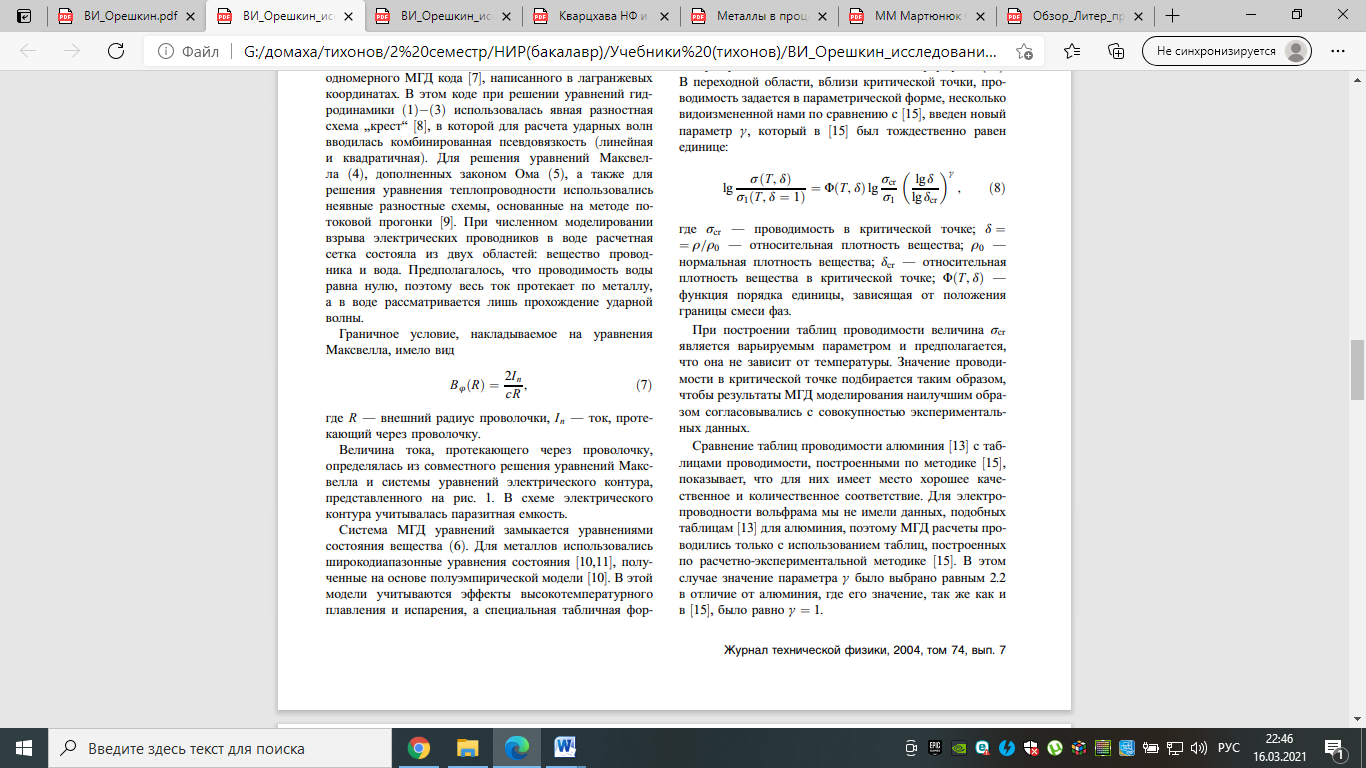



где R — внешний радиус проволочки, In — ток, протекающий через проволочку. Величина тока, протекающего через проволочку, определялась из совместного решения уравнений Максвелла и системы уравнений электрического контура. В схеме электрического контура учитывалась паразитная емкость. Система МГД уравнений замыкается уравнениями состояния вещества (6). Для металлов использовались широкодиапазонные уравнения состояния, полученные на основе полуэмпирической модели. В этой модели учитываются эффекты высокотемпературного плавления и испарения, а специальная табличная форма УРС дает возможность учесть метастабильные состояния жидкости и газа на фазовой диаграмме. Для воды было использовано УРС. В расчетах для определения электропроводности алюминия использовалось два различных метода. В первом электропроводность алюминия определялась по таблицам проводимости, составленным М. Дежарли в Национальной Лаборатории Сандия (США) на основе модели, модифицированной с учетом экспериментальных данных. Во втором электропроводность определялась по расчетно-экспериментальной методике, в которой проводимость рассматривается как некая эмпирическая функция плотности и удельной энергии, вложенной в вещество. Кроме того, в этой методике проводимость параметрически зависит от конкретного вида уравнения состояния вещества. Таблицы проводимости в рамках этой методики строятся таким образом. Имеются следующие исходные данные:

1) зависимость σ1(T, δ = 1) при нормальной плотности вещества, которая является табличной величиной;

2) зависимость проводимости в газоплазменной области, которая рассчитывается по классическим формулам. В переходной области, вблизи критической точки, проводимость задается в параметрической форме, несколько видоизмененной нами по сравнению с, введен новый параметр γ, который был тождественно равен единице: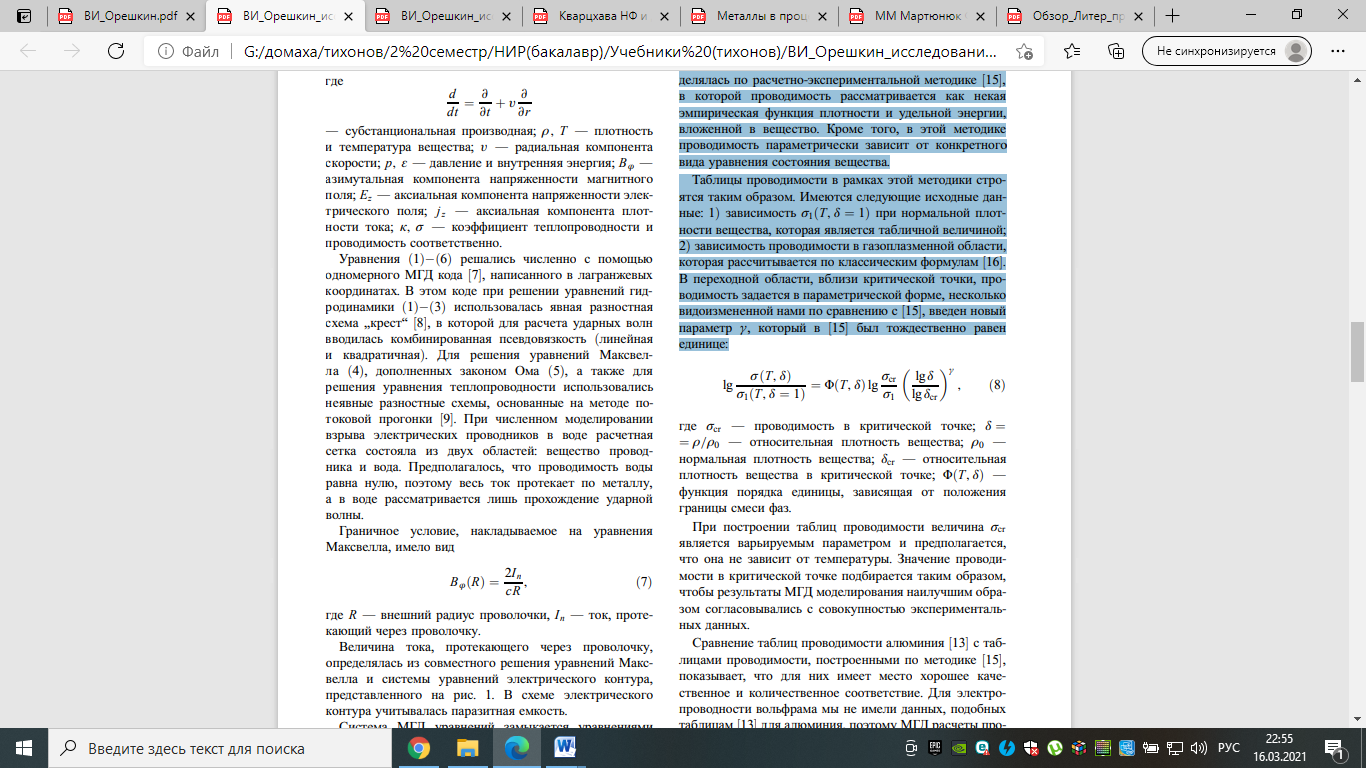



где σcr — проводимость в критической точке; δ = = ρ/ρ0 — относительная плотность вещества; ρ0 — нормальная плотность вещества; δcr — относительная плотность вещества в критической точке; (T, δ) — функция порядка единицы, зависящая от положения границы смеси фаз. При построении таблиц проводимости величина σcr является варьируемым параметром и предполагается, что она не зависит от температуры. Значение проводимости в критической точке подбирается таким образом, чтобы результаты МГД моделирования наилучшим образом согласовывались с совокупностью экспериментальных данных. Сравнение таблиц проводимости алюминия с таблицами проводимости, построенными по методике, показывает, что для них имеет место хорошее качественное и количественное соответствие. Для электропроводности вольфрама мы не имели данных, подобных таблицам для алюминия, поэтому МГД расчеты проводились только с использованием таблиц, построенных по расчетно-экспериментальной методике. В этом случае значение параметра γ было выбрано равным 2.2 в отличие от алюминия, где его значение, так же как и в, было равно γ = 1.[5]