Электромагнетизм
 Скачать 319.28 Kb. Скачать 319.28 Kb.
|
|
Электромагнетизм 1. Вращающий момент, действующий на рамку с током со стороны магнитного поля. Магнитный момент рамки с током. Вращающий момент. Определение индукции магнитного поля. Единицы индукции и вращающего момента. Поместив рамку в однородное магнитное поле, на нее действует пара сил, которая создает вращающий момент. 2. Напряженность магнитного поля и ее связь с индукцией. Единица напряженности. Вектор магнитной индукции является общей характеристикой точек магнитного поля независимо от того, как создается магнитное поле: намагниченным телом или проводником с током находящимся в данной среде. Однако можно ввести некоторую характеристику магнитного поля не зависящую от среды, а определяющуюся токами и конфигурацией проводников - вектор напряженности магнитного поля. Эти две характеристики (одна общая, а другая частная) связаны между собой: 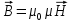 где где 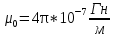 - абсолютная магнитная проницаемость вакуума, μ — относительная магнитная проницаемость среды, для вакуума μ = 1. - абсолютная магнитная проницаемость вакуума, μ — относительная магнитная проницаемость среды, для вакуума μ = 1.Напряженностью магнитного поля – отношение механической силы, действующей на положительный полюс пробного магнита, к величине его магнитной массы или механическая сила, действующая на положительный полюс пробного магнита единичной массы в данной точке поля. Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4π* 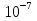 Тл. Тл.3. Изображение магнитных полей с помощью силовых линий индукции (напряженности). Вид линий магнитной индукции прямого и кругового токов, соленоида. Правила, но которым определяют направление линий магнитной индукции. 4. Магнитные поля проводников с токами. Закон Био-Савара-Лапласа. Магнитное поле – это силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения. Закон Био-Савара-Лапласа: В векторной форме: 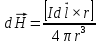 В скалярной форме: 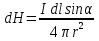 5. Применение закона Био-Савара-Лапласа для определения напряженности поля, создаваемого: а) прямым проводником конечной длины (вывод формулы) б) бесконечно длинным прямым проводником (вывод формулы) в) круговым проводником в центре (вывод формулы) г) соленоидом и тороидом д) круговым проводником на оси (без вывода) 6. Сила Ампера. Правило для определения направления силы Ампера. На проводник с током, находящийся в магнитном поле, действует сила, равная F = I·L·B·sina I - сила тока в проводнике; B - модуль вектора индукции магнитного поля; L - длина проводника, находящегося в магнитном поле; a - угол между вектором магнитного поля инаправлением тока в проводнике. Сила Ампера – Сила, действующую на проводник с током в магнитном поле. Максимальная сила Ампера равна: F = I·L·B. Ей соответствует a = 90. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера. 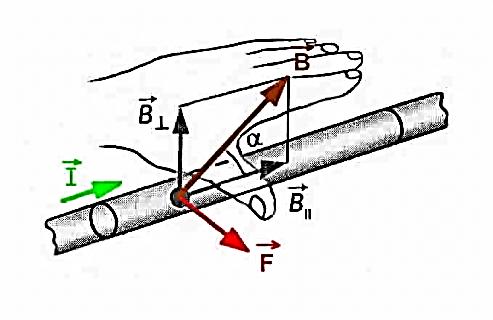 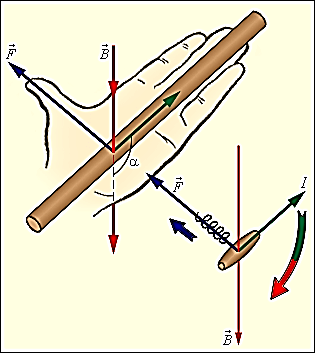 7. Сила взаимодействия двух параллельных проводников с токами (вывод).Определение единицы силы тока. 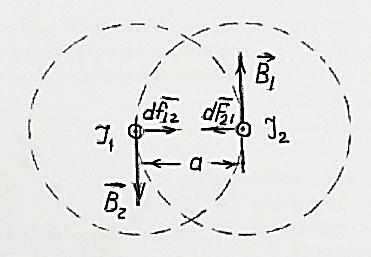 Каждый из проводников создаёт магнитное поле, которое действует по закону Ампера на второй проводник. Ток Каждый из проводников создаёт магнитное поле, которое действует по закону Ампера на второй проводник. Ток 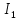 создаёт вокруг себя магнитное поле, линии магнитной индукции которого создаёт вокруг себя магнитное поле, линии магнитной индукции которогопредставляют собой концентрические окружности. Направление вектора В задаётся правилом правого винта, его модуль равен 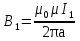 Направление силы d 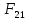 с которой поле с вектором с которой поле с вектором 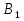 действует на участок dL второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, с учётом того, что угол между элементами тока действует на участок dL второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, с учётом того, что угол между элементами тока  и вектором и вектором  прямой, равен: прямой, равен:  Аналогичными рассуждениями можно показать, что на участок dl первого проводника действует сила  направленная в сторону, противоположную направленная в сторону, противоположную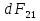 и численно равна: и численно равна: 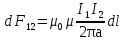 Сравнение выражений показывает, что 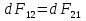 т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой 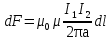 Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания. Полагая  имеем имеем  Магнитные линии двух проводников с токами разных направлений в пространстве между проводниками направлены в одну сторону. Магнитные линии, имеющие одинаковое направление, будут взаимно отталкиваться. Поэтому проводники с токами противоположного направления отталкиваются один от другого За единицу силы тока 1 А принимают силу тока, при которой два параллельных проводника длиной 1м, расположенные на расстоянии 1м друг от друга, взаимодействуют с силой 0,0000002 Н. 8. Действие магнитного поля на движущийся заряд. Сила Лоренца. Определение направления силы Лоренца. Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.   Сила Лоренца – сила, действующая со стороны магнитного поля на движущиеся в нем заряды. 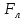 = q·V·B·sina = q·V·B·sinaгде q - величина движущегося заряда; V - модуль его скорости; B - модуль вектора индукции маг. поля; a - угол м/у вектором скорости заряда и вектором маг. инд. Cила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно. Сила Лоренца перпендикулярна векторам В и v , и её направление определяется по правилу: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л. Сила Лоренца зависит от модулей скорости частицы и индукции магнитного поля. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Частица равномерно движется по окружности радиуса r. 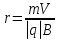 9. Движение заряженных частиц в однородном магнитном поле: а) вектор индукции параллелен вектору скорости частицы; б) перпендикулярен ему; в) составляет угол а с направлением скорости частицы. Вычисление радиуса окружности, периода обращения и шага винтовой линии. 22. Природа диамагнетизма 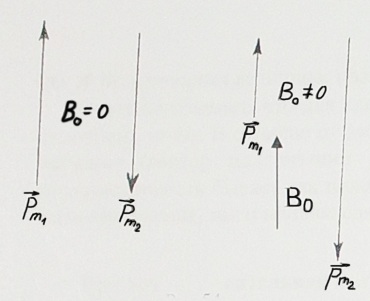 Если полный магнитный момент каждого атома в отсутствии поля равен нулю: Если полный магнитный момент каждого атома в отсутствии поля равен нулю: 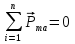 ,то вещество, состоящее из таких атомов, называется диамагнитным. ,то вещество, состоящее из таких атомов, называется диамагнитным.Допустим, что именно это и имеет место при четном числе электронов в атоме и симметричном расположении орбит (рис.). Кроме того, предположим для простоты, что все орбиты расположены в параллельных плоскостях, и вектор индукции намагничивающего поля перпендикулярен этим плоскостям. При внесении диамагнитного атома в магнитное поле происходит следующее: если в отсутствие поля магнитные моменты атомов компенсировали друг друга (на рисунке представлены две орбиты, одна из которых имеет вектор магнитного момента направленный по полю, а вторая орбита имеет вектор  поля), то в присутствии поля вследствие прецессии орбит орбитальный момент одной будет уменьшаться, а второй увеличиваться, так что в целом суммарный магнитный момент будет направлен против внешнего поля, в целом все вещество приобретает магнитный момент, направленный против поля и таким образом создается добавочное магнитное поле с индукцией В’ направленной против основного поля: B= поля), то в присутствии поля вследствие прецессии орбит орбитальный момент одной будет уменьшаться, а второй увеличиваться, так что в целом суммарный магнитный момент будет направлен против внешнего поля, в целом все вещество приобретает магнитный момент, направленный против поля и таким образом создается добавочное магнитное поле с индукцией В’ направленной против основного поля: B= Диамагнитный эффект не зависит от температуры, так как тепловое движение атомов не нарушает ориентации индуцированных токов внутри атомов. Только атомы с заполненными электронными оболочками обладают чистым диамагнитным эффектом. К ним относятся гелий и другие инертные газы, однократно ионизированные атомы лития, натрия, меди, а также висмут, вода, ртуть. 23. Природа парамагнетизма.  Если магнитный момент Если магнитный момент  отдельного атома отличен от нуля, вещество называется парамагнитным (например, вследствие нечетного числа электронов в атоме). В отсутствие внешнего магнитного поля тепловое движение создает беспорядок и магнитные моменты отдельных атомов ориентированы в пространстве хаотически и вещество оказывается не намагниченным (рис.): отдельного атома отличен от нуля, вещество называется парамагнитным (например, вследствие нечетного числа электронов в атоме). В отсутствие внешнего магнитного поля тепловое движение создает беспорядок и магнитные моменты отдельных атомов ориентированы в пространстве хаотически и вещество оказывается не намагниченным (рис.): 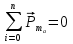 При создании поля с индукцией 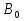 оно стремится установить магнитные моменты атомов вдоль оно стремится установить магнитные моменты атомов вдоль 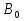 , тепловое движение стремится разбросать их равномерно по всем направлениям. В результате устанавливается некоторая преимущественная ориентация моментов вдоль поля тем большая, чем больше индукция внешнего магнитного поля , тепловое движение стремится разбросать их равномерно по всем направлениям. В результате устанавливается некоторая преимущественная ориентация моментов вдоль поля тем большая, чем больше индукция внешнего магнитного поля 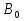 , и тем меньшая, чем выше температура. , и тем меньшая, чем выше температура.Таким образом, полный вектор магнитной индукции для парамагнитного вещества равен: B=  Конечно, и в парамагнитных телах имеет место диамагнитный эффект, но он перекрывается эффектом ориентации магнитных моментов атомов по полю. К парамагнитным веществам относятся натрий, калий, свинец, большая часть стекол, газообразный и жидкий кислород. 24. Намагниченность (вектор намагничения). Его связь с напряженностью внешнего магнитного поля. Относительная магнитная проницаемость. В общем случае возникающее добавочное магнитное поле зависит не только от свойств вещества, но и от размеров этого тела и от его формы (шар, стержень, замкнутое кольцо и так далее). Намагничение магнетика можно характеризовать магнитным моментом единицы объема. Эту величину называют намагниченностью (вектор намагничевания вещества) и обозначают буквой J. Это суммарный магнитный момент всех молекул, атомов и электронов, имеющихся в единице объема.  где  - физически бесконечно малый объем, - физически бесконечно малый объем,  - магнитный момент отдельной молекулы (атома, электрона). Суммирование производится по всем молекулам (атомам, электронам), заключенных в объем ΔV. - магнитный момент отдельной молекулы (атома, электрона). Суммирование производится по всем молекулам (атомам, электронам), заключенных в объем ΔV.Намагничивание любого вещества определяется свойствами его оставляющих элементов (атомов, молекул, электронов), поэтому существует определенная связь, как показывает опыт, между вектором намагничевания J и напряженностью внешнего магнитного тока 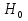 (отклик на (отклик на 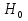 магнетиком) H ’=J=ϗ* магнетиком) H ’=J=ϗ*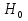 где ϗ- безразмерная величина, называемая магнитной восприимчивостью вещества. Опыт показывает, что для слабомагнитных (неферромагнитных) веществ при не слишком сильных полях ϗ не зависит от 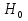 . В отличие от диэлектрической восприимчивости χ , которая может иметь лишь положительные значения (вектор поляризации Р в избранном диэлектрике всегда направлена по полю Е), магнитная восприимчивость бывает как положительной, так и отрицательной. Поэтому магнитная проницаемость μ может быть как больше, так и меньше единицы. Они связаны простым соотношением μ=1 ± ϗ . В отличие от диэлектрической восприимчивости χ , которая может иметь лишь положительные значения (вектор поляризации Р в избранном диэлектрике всегда направлена по полю Е), магнитная восприимчивость бывает как положительной, так и отрицательной. Поэтому магнитная проницаемость μ может быть как больше, так и меньше единицы. Они связаны простым соотношением μ=1 ± ϗПри этом относительная магнитная проницаемость р, показывает во сколько раз изменяется магнитное поле в магнетике по сравнению с вакуумом:  Вещества, для которых μ < 1, называются диамагнетиками (диамагнитными), а вещества с μ > 1 -парамагнетиками (парамагнитными). Так как магнитная проницаемость связана с магнитной восприимчивостью μ = 1 ± ϗ, то для парамагнетиков ϗ положительна, а для диамагнетиков - отрицательна. Cама величина ϗ невелика: для парамагнетиков она составляет порядка  , убывающая при нагревании вещества и практически независящая от индукции, а для диамагнетиков она равна - , убывающая при нагревании вещества и практически независящая от индукции, а для диамагнетиков она равна -  и не зависит ни от температуры, ни от индукции, т.е. относительная магнитная проницаемость мало отличается от единицы, например, для платины равна 1,00036. и не зависит ни от температуры, ни от индукции, т.е. относительная магнитная проницаемость мало отличается от единицы, например, для платины равна 1,00036.25. Ферромагнетики. Особенности свойств ферромагнетиков. Магнитный гистерезис. Природа ферромагнетизма. Точка Кюри. Ферромагнетики - вещества, способные намагничиваться весьма сильно  Зависимость В от Зависимость В от 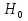 . Сначала индукция результирующего поля растет довольно быстро от напряженности внешнего магнитного поля . Сначала индукция результирующего поля растет довольно быстро от напряженности внешнего магнитного поля 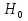 , а затем, после перегиба, увеличивается линейно только за счет магнитного поля тока, ибо процесс намагничивания ферромагнетика закончился. Это состояние вещества Столетов назвал магнитным насыщением. Такой характер зависимости можно объяснить следующим образом: сначала под действием поля заметно возрастает степень ориентации магнитных моментов по полю, однако постепенно степень ориентации становится все меньше, пока не заканчивается вовсе. , а затем, после перегиба, увеличивается линейно только за счет магнитного поля тока, ибо процесс намагничивания ферромагнетика закончился. Это состояние вещества Столетов назвал магнитным насыщением. Такой характер зависимости можно объяснить следующим образом: сначала под действием поля заметно возрастает степень ориентации магнитных моментов по полю, однако постепенно степень ориентации становится все меньше, пока не заканчивается вовсе.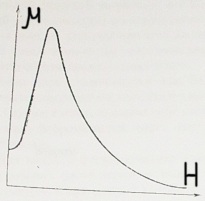 график зависимости магнитной проницаемости μ от напряженности внешнего поля график зависимости магнитной проницаемости μ от напряженности внешнего поля 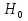 Вначале μ растет с увеличением Н, затем, достигая максимума, начинает уменьшаться, стремясь в случае сильных полей к 1 (  ) = 1 + J/H, поэтому при J = Jнас = const с ростом Н отношение J/H →0, μ→1). ) = 1 + J/H, поэтому при J = Jнас = const с ростом Н отношение J/H →0, μ→1).Характерная особенность ферромагнетиков состоит также в том, что для них зависимость J от H (а следовательно, и В от Н) определяется предысторией намагничения ферромагнетика. Это явление получило название магнитного гистерезиса. Природа ферромагнетизма Первая попытка объяснения главной особенности ферромагнетиков - способности сильно намагничиваться принадлежит русскому ученому Розингу, коротый предложил, что даже в ненамагниченном ферромагнетике действуют силы, которые вызывают намагничение отдельных участков образца. Основы теории ферромагнетизма были созданы Френкелем и Гейзенбергом. В ферромагнетике возникают области самопроизвольного намагничивания до состояния насыщения, которые называются доменами. Домены - это отдельные микроскопические области кристалла, имеющие размеры от  до до  (1-10 мкм.) и содержащие до (1-10 мкм.) и содержащие до  ионов, в которых спины расположены параллельно друг другу (намагничены до насыщения). ионов, в которых спины расположены параллельно друг другу (намагничены до насыщения).В пределах каждого домена ферромагнетик обладает определенным магнитным моментом. Направления этих моментов для разных доменов различны, так что в отсутствие внешнего поля суммарный момент всего тела равен нулю. При включении внешнего поля энергия отдельных доменов делается неодинаковой: энергия меньше для тех доменов, в которых вектор намагничивания образует с направлением поля острый угол, и больше в том случае если этот угол тупой Поэтому возникает процесс смещения границ доменов, при котором объем доменов с меньшей энергией возрастает, а с большей энергией уменьшается. Те домены, у которых вектор J составляет малый угол с вектором внешнего магнитного поля начинают поглощать другие домены, вызывая при этом их смещение и поворот. В конце концов при некотором значении индукции мы получаем как бы один домен с вектором магнитного момента еще не параллельным полю. Если поле увеличивается еще больше, то возникает новый тип процесса намагничивания, при котором изменяется направление магнитного момента внутри домена. Наконец в очень сильном поле магнитные моменты всех доменов устанавливаются параллельно полю. В этом состоянии ферромагнетик имеет наибольший при данной температуре магнитный момент, т.е. намагничен до насыщения. Для каждого ферромагнетика имеется определенная температура Тс , при которой области спонтанного намагничения распадаются и вещество утрачивает ферромагнитные свойства. Эта температура называется температурой Кюри (точкой Кюри). Для железа она равна 768 С, для никеля 365 °С. При температуре выше точки Кюри ферромагнетик становится обычным парамагнетиком Существуют особые ферромагнитные материалы (ферриты или ферримагнетики) отличающиеся тем, что они обладают высокой магнитной восприимчивостью и проницаемостью (ц. доходит до 20000), малой коэрцитивной силой, малыми потерями на перемагничивание и очень большим удельным электросопротивлением (до 1014 Ом-м), благодаря чему они получили широкое применение в радиотехнике (потери на токи Фуко в ферритах, находящихся в высокочастотных электромагнитных полях, очень малы). Ферритовые сердечники применяются в электронно-счетных машинах, радиолокационных, телефонных, электроакустических и прочих аппаратурах. |
