Отчет(1). Электростатического поля заряженных проводников методом моделирования
 Скачать 92 Kb. Скачать 92 Kb.
|
|
ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ЗАРЯЖЕННЫХ ПРОВОДНИКОВ МЕТОДОМ МОДЕЛИРОВАНИЯ (электроемкость, энергия электрического поля) Цель работы: Ознакомление с методикой моделирования электростатического поля в токопроводящей среде, исследование электростатического поля, созданного системой проводящих тел, экспериментальное определение электроемкости системы проводников. Приборы и принадлежности: лабораторный макет установки для моделирования электростатического поля (рис. 1). В работе используется планшет (1), покрытый проводящей бумагой, с нанесенными на него металлическими электродами (2). На планшете установлены две подвижные линейки (3), с помощью которых определяются координаты щупа (4), подключенного к вольтметру (pV). Помещая щуп в различные точки планшета, и, измеряя потенциал данной точки, можно построить картину исследуемого поля. Исследуемые закономерности М 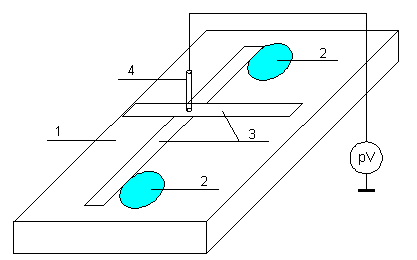 одель электростатического поля. В проводящей среде под действием приложенной к электродам постоянной разности потенциалов происходит направленное движение заряженных частиц, в результате которого в среде, окружающей электроды, устанавливается стационарное распределение потенциала, подобное распределению потенциала в диэлектрической среде вокруг заряженных проводящих тел, если форма и взаимное расположение последних аналогичны соответствующим параметрам электродов проводящей модели. одель электростатического поля. В проводящей среде под действием приложенной к электродам постоянной разности потенциалов происходит направленное движение заряженных частиц, в результате которого в среде, окружающей электроды, устанавливается стационарное распределение потенциала, подобное распределению потенциала в диэлектрической среде вокруг заряженных проводящих тел, если форма и взаимное расположение последних аналогичны соответствующим параметрам электродов проводящей модели. Сопоставление свойств электростатического поля и поля электрического тока в проводящей среде показывает, что если в электростатическом поле на помещенный в поле заряд действует сила 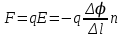 , (1) , (1)где n – единичный вектор в направлении максимального изменения потенциала, то в проводящей среде вектор плотности тока подчиняется вполне симметричному соотношению 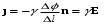 , (2) , (2)где - электропроводность среды (величина, обратная удельному сопротивлению). Из сопоставления этих двух соотношений видно, что, во-первых, оба поля потенциальны, т.е. не образуют вихрей в пространстве, окружающем электроды, а, во-вторых, как линии напряженности электростатического поля, так и линии тока перпендикулярны линиям или поверхностям равного потенциала. Поле длинной двухпроводной линии. На планшете моделируются так называемые плоские поля, т.е. такие поля, картина которых остается неизменной при параллельном переносе плоскости, в которой производится исследование поля. Как правило, – это электростатические поля объектов, бесконечно протяженных в направлении, перпендикулярном секущей п 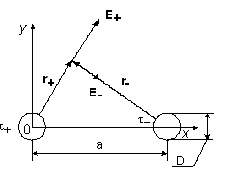 лоскости. В данной работе исследуется поле двух длинных, параллельных, равномерно и разноименно заряженных проводящих цилиндров (двухпроводной линии). лоскости. В данной работе исследуется поле двух длинных, параллельных, равномерно и разноименно заряженных проводящих цилиндров (двухпроводной линии).Если абсолютная величина линейной плотности заряда на цилиндрах (Кл/м), то напряженность электростатического поля в произвольной точке секущей плоскости будет определяться геометрической суммой напряженностей полей, создаваемых каждым цилиндром (принцип суперпозиции). Для каждого из цилиндров абсолютная величина напряженности поля 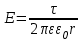 , (3) , (3)а величину и направление результирующего вектора напряженности поля определяют по отношению к системе координат x0y (рис.2), заданной экспериментатором. Напряженность поля и вектор индукции. Для электростатического поля справедливо следующее соотношение между вектором напряженности поля и вектором электрической индукции 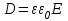 . (4) . (4)Особенность вектора электрической индукции состоит в том, что, описывая с помощью этой физической величины электрическое поле, исследователь избавляется от необходимости учитывать связанные заряды, возникающие при поляризации среды. Электроемкость. Часто источниками электростатического поля служат заряженные проводящие тела. В этих случаях важным является знание электроемкости тел, несущих электрические заряды. Электроемкость определяют как отношение заряда, находящегося на проводящем теле к возникающему при этом потенциалу этого тела 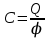 , ,или если речь идет о системе заряженных тел, например, конденсаторе, то электроемкость равна отношению заряда, находящегося на одном из тел, к разности потенциалов между этими телами 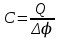 . .В конденсаторе электрическое поле полностью локализовано в объеме конденсатора. Электроемкость измеряют в Фарадах (Ф). Электроемкость проводников зависит от размеров тел и их взаимного расположения. Например, электроемкость уединенного проводящего шара радиуса R 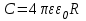 . .Для плоского, цилиндрического и сферического конденсаторов их электроемкости определяются, соответственно, как 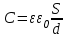 , , 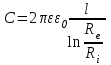 , , 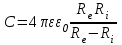 , ,где S – площадь пластины плоского конденсатора, d – расстояние между пластинами, l – длина цилиндрического конденсатора, Re, Ri – соответственно, радиусы внешней и внутренней обкладок цилиндрического или сферического конденсатора. Энергия электрического поля. Конденсаторы, по сути, являются накопителями электрической энергии. Известно, что энергия заряженного конденсатора определяется эквивалентными соотношениями 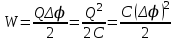 . .Для объемной плотности энергии электрического поля используют выражение 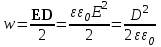 . .Основные расчетные формулы 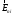 1)Модуль нормальной составляющей вектора напряженности. Вектор напряженности из связи между напряженностью и потенциалом равен 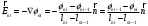 Соответственно, его длина составит 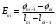 где φni-1 – потенциал в i-йточке внутреннего контура, φni – потенциал в i-й точке внешнего контура; lni, lni-1 – координаты i-й точки, нормальные к контуру (x или у). Погрешность. Воспользуемся методом переноса погрешностей. 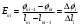 Для 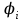 и и 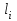 считаем, что случайных погрешностей нет. считаем, что случайных погрешностей нет.При расчете 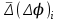 и и 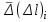 учитываем, что приборные погрешности учитываем, что приборные погрешности 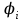 и и 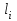 одинаковые и складываем их линейно. одинаковые и складываем их линейно.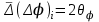 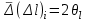 Итоговая погрешность равна 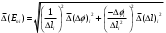 Аналогичные формулы для расчета напряженности на линии, соединяющей два электрода, но l=x. 3)Линейная плотность моделируемого заряда Q (из напряженности между электродами) 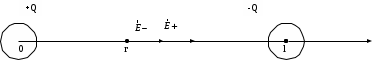 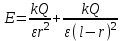 т. е. т. е. 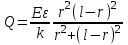 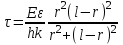 где E- напряженность в точке r, Q- заряд электрода, l- расстояние между электродамиh – высота электрода. 4)Электроемкость С (из напряженности между электродами) C=Q/U = 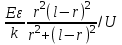 где E- напряженность в точке r, Q- заряд электрода, l- расстояние между электродами, U-напряжение, равное разности потенциалов между электродами модели. 5)Поток вектора индукции ФD. 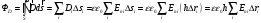 где Δri – длина отрезка, содержащего i-ю точку, Eni – нормальная составляющая напряженности в i-й точке поля, h – высота электрода. 6) Линейная плотность моделируемого заряда Q (из потока индукции) По теореме Гаусса 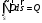 Линейная плотность τ =Q/h= 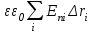 где Δri – длина отрезка, содержащего i-ю точку, Eni – нормальная составляющая напряженности в i-й точке поля. 7)Электроемкость С (из потока индукции) C=Q/U = 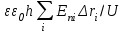 где Δri – длина отрезка, содержащего i-ю точку, Eni – нормальная составляющая напряженности в i-й точке поля, h – высота электрода, U-напряжение, равное разности потенциалов между электродами модели. Обработка результатов 1) Рассчитаем значение напряженности вдоль линии, соединяющей электроды, а также погрешность.
2) Рассчитаем линейную плотность моделируемого заряда (h=3 см, ε=1) 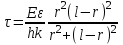 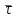 =1*10-10 Кл/м =1*10-10 Кл/м3) Рассчитаем электроемкость. С= 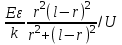 =0,6*10-9Ф =0,6*10-9Ф4) Рассчитаем значение нормальной составляющей напряженности на отрезках контура, а также погрешность.
5) Рассчитаем поток вектора индукции (h=3 см, ε=1) 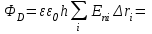 5,96 * 10-12 Кл 5,96 * 10-12 Кл6) Рассчитаем линейную плотность моделируемого заряда (h=3 см, ε=1) τ = 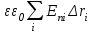 =2*10-10 Кл/м =2*10-10 Кл/м7) Рассчитаем электроемкость. С= 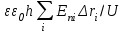 =1,3*10-9Ф =1,3*10-9ФВывод. Проделав работу, я исследовал электростатическое поле, созданное системой проводящих тел. Обнаружил, что максимумы нормальных составляющих напряженностей в точках, принадлежащих контуру, охватывающему электрод, расположены вблизи центра электрода. Напряженность на линии, соединяющей два электрода, принимает наибольшие значения вблизи электродов и убывает при удалении от них. Данные закономерности соответствуют карте поля двух зарядов. Кроме того, я определил электроемкость системы проводников. Оба результата (из потока индукции и из напряженности между электродами) равны в пределах погрешностей. |
