Физика задачи. кр физика 6 задач. Электростатика Два одинаковых небольших шарика, массой т 0,1 г каждый, подвешены в одной точке на одинаковых нитях длиной l 25 см.
 Скачать 52.89 Kb. Скачать 52.89 Kb.
|
|
Электростатика 1. Два одинаковых небольших шарика, массой т = 0,1 г каждый, подвешены в одной точке на одинаковых нитях длиной l = 25 см. Шарикам сообщили одинаковые заряды, после чего они разошлись на расстояние х = 5 см. Определить модуль заряда, сообщенного каждому шарику. Решение: 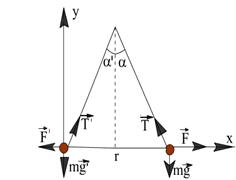 На каждый из отклоненных шариков действуют: m 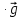 - сила тяжести, - сила тяжести, 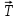 сила натяжения нити, сила натяжения нити, 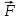 - кулоновская сила взаимодействия шариков (см. рис.). Запишем условие равновесия одного из шариков в векторной форме: - кулоновская сила взаимодействия шариков (см. рис.). Запишем условие равновесия одного из шариков в векторной форме:m 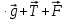 = 0 = 0 Спроецируем это уравнение на координатные оси Х и Y: X: T× sinα – F = 0; Y: T× cosα – mg = 0 Исключая из этих уравнений Т, получаем 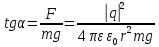 Так как 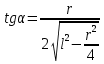 , то , то 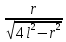 = =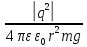 Тогда 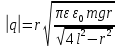 Поскольку 4l2>>r, то 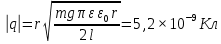 Электрмагнетизм 2. На концах тонкого непроводящего горизонтального стержня длиной l =1м закреплены две маленькие бусинки, а третья надета на стержень, по которому она может перемещаться без трения. Всем бусинкам сообщают одинаковые заряды q=10-6 Кл. Найти период малых колебаний подвижной бусинки. Масса бусинки m=5 г. Решение: Период колебаний бусинки может быть рассчитан по формуле: 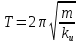 k - некоторый коэффициент, играющий роль коэффициента жесткости. Он может быть определен из соотношения: 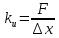 Где 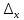 - смещение бусинки из положения равновесия. - смещение бусинки из положения равновесия.Сила, действующая на бусинку при выходе из положения равновесия (возвращающая сила F ) может быть записана как равнодействующая двух сил, действующих на бусинку со стороны обоих зарядов: 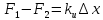 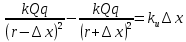 Приведем к общему знаменателю левую часть: 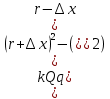 Упростим: 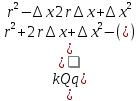 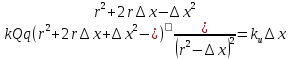 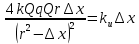 Откуда 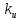 : :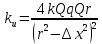 Тогда период колебаний равен: 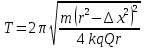 Так как величина 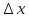 очень маленькая – ведь речь идет о малых колебаниях – то ею можно пренебречь. Кроме того, q=Q . Тогда: очень маленькая – ведь речь идет о малых колебаниях – то ею можно пренебречь. Кроме того, q=Q . Тогда:Так как 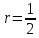 , то , то 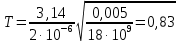 Ответ: 0,83 с 3. Металлический шар радиуса R1, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R2. Определите потенциал шара φ1 после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают. Решение. До соединения сфер проводником заряд первой был равен: 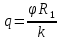 После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением: 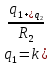 где q1 и q2 — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q1 + q2. После несложных преобразований получаем: 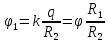 4. Две спирали из различных материалов соединены параллельно. Отношение их длин 15:14, а площадей поперечных сечений 5:4. Оказалось, что за одинаковое время в них выделяется одинаковое количество теплоты. Определить отношение удельных сопротивлений этих материалов. Введем параметры для простоты расчетов p1/p2 = x - ? L1/L2 = a = 15/14 S1/S2 = b = 5/4 по условию Q1 = Q2. если допустить, что в обоих случаях одинакова также сила тока, то получим, что R1 = R2 (p1· L1)/S1 = (p2· L2)/S2. Преобразуем в уравнение разделим обе части на p2. получим: (x· L1)/S1 = L2/S2 разделим обе части на L2. получим: (x· a)/S1 = 1/S2 умножим обе части на S1. получим: x ·a = b, x = b / a. x = (5/4) · (14/5) = 7/6 Магнетизм 5. Какую ускоряющую разность потенциалов U должна пройти частица массой m = 0,5мг и зарядом q = 2мкКл, чтобы в однородном магнитном поле индукцией B = 5мТл на неё действовала бы сила F = 2·10-5 Н? Магнитное поле направлено перпендикулярно скорости частицы. Начальная скорость частицы v0 = 0. Решениеm = 0,5 мг = 0,5 ·10-3 кг. q = 2 мкКл = 2 ·10-6 Кл. Fл = 2 ·10-6 Н. ∠α = 90° B = 5 мТл = 5 *10-3 Тл. V0 = 0 м/с. U - ? На движущейся заряд в магнитном поле действует сила Лоренца Fл, значение которой определяется формулой: Fл = q ·B ·V ·sinα, где q - величина заряда, B - магнитная индукция поля, V - скорость движения заряда, ∠α - угол между магнитной индукцией B и скоростью движения V. Так как V и В взаимно перпендикулярны, то sin 90°= 1. Формула для определения скорости частицы V примет вид: V = Fл / q ·В. V = 2 ·10-6 Н/2 ·10-5 Кл ·5 ·10-3 Тл = 200 м/с. Работа электрического поля А равна изменению кинетической энергии частицы ΔЕк: А = ΔЕк. ΔЕк = m ·V2 /2. А = q ·U. m ·V2 /2 = q ·U. U = m ·V2 /2 ·q. U = 0,5 ·10-3 кг · (200 м/с)2 /2 ·2 ·10-5 Кл = 125 МВ. Ответ: частица прошла разность потенциалов U = 125 МВ. 6. Металлический стержень длиной 20 см подвесили горизонтально на двух легких проводах длиной 10 см в вертикальном магнитном поле, модуль индукции которого 1,0 Тл. Стержень отклоняют на 30° от положения равновесия и отпускают (рис. 2). Разность потенциалов между концами стержня в тот момент, когда он проходит положение равновесия, составляет:  Решение Будем считать, что возникает ЭДС, но сила тока через стержень пренебрежимо мала настолько, что ток в стержне не создает магнитного поля и это поле не воздействует с внешним полем, тогда: По ЗСЭ найдем скорость стержня в нижней точке. mgh=mgR  (1-cos(30))=mv2/2 (1-cos(30))=mv2/2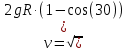 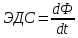 В нижней точке 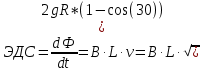 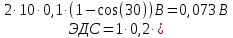 Ответ: 0,073 В |
