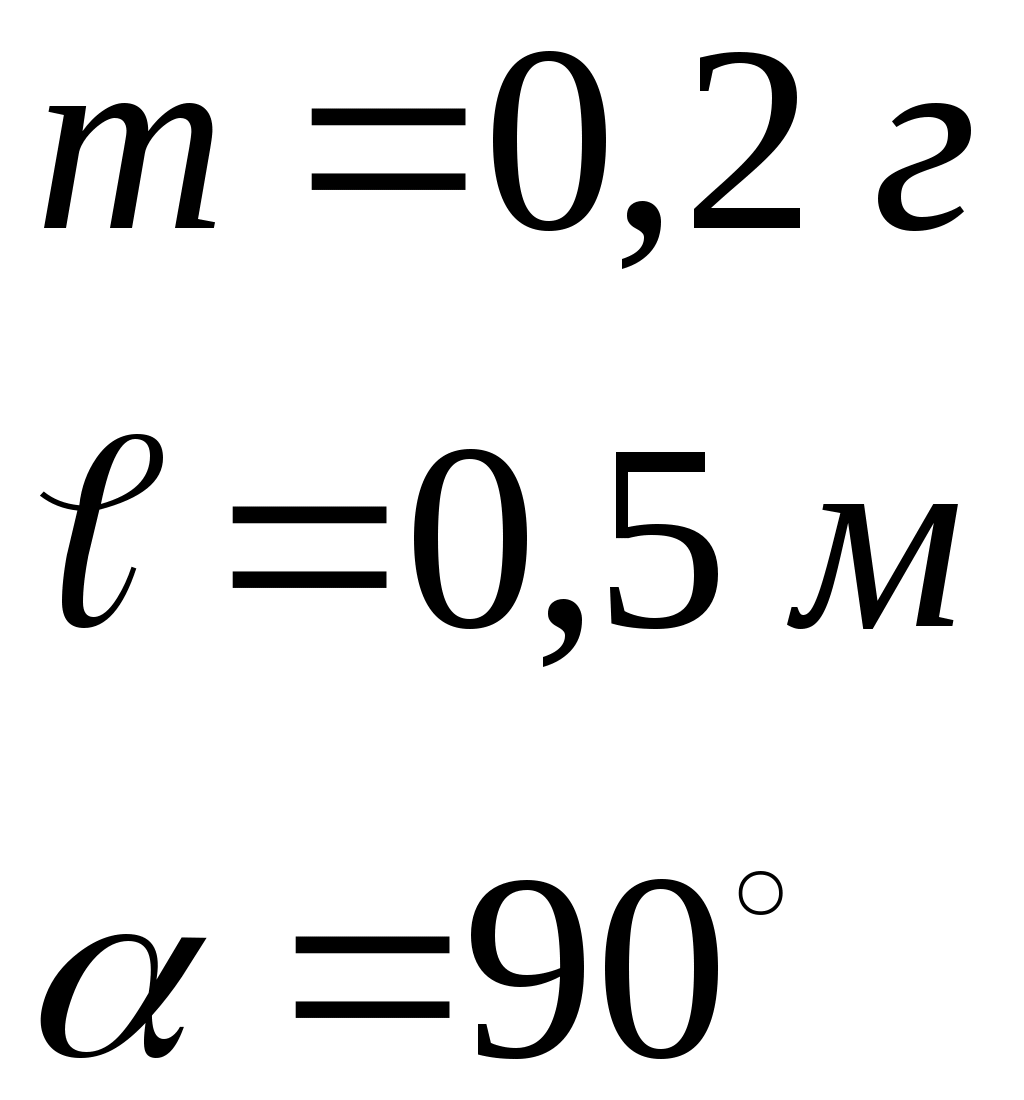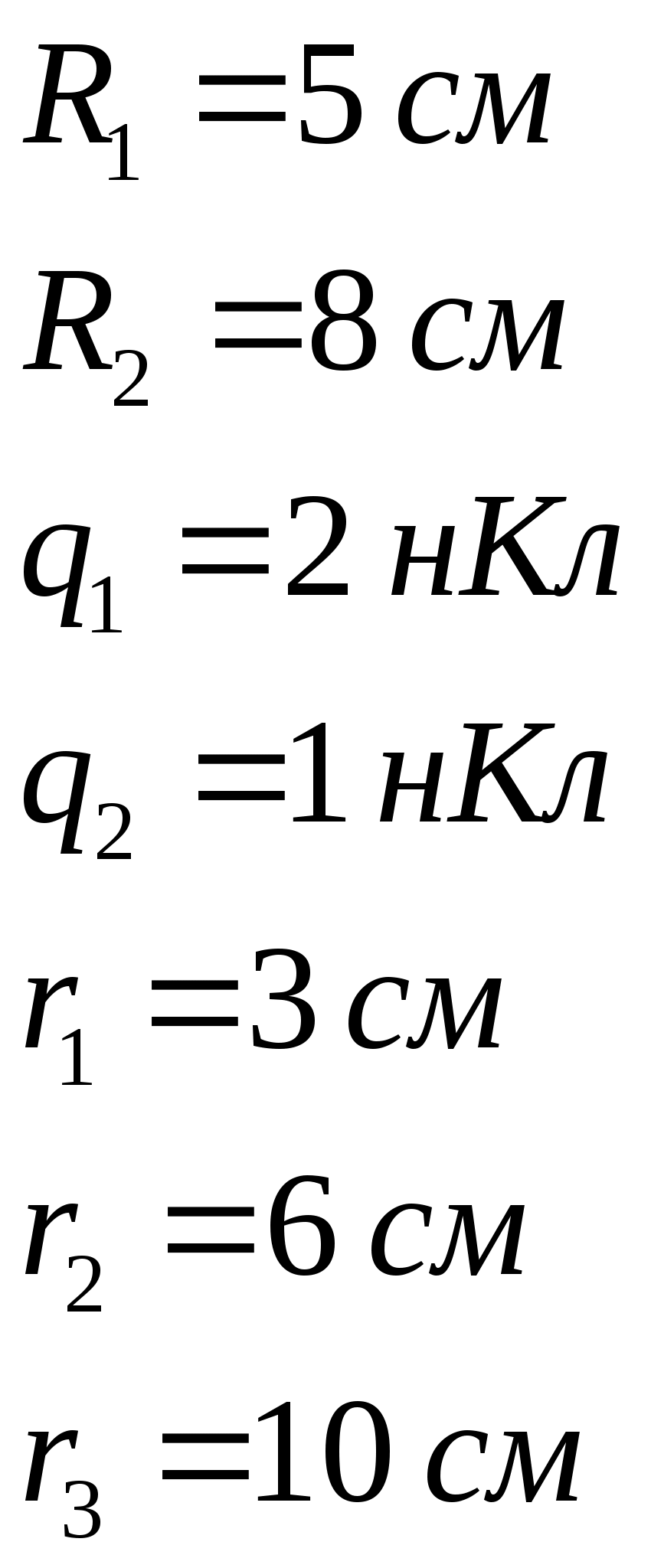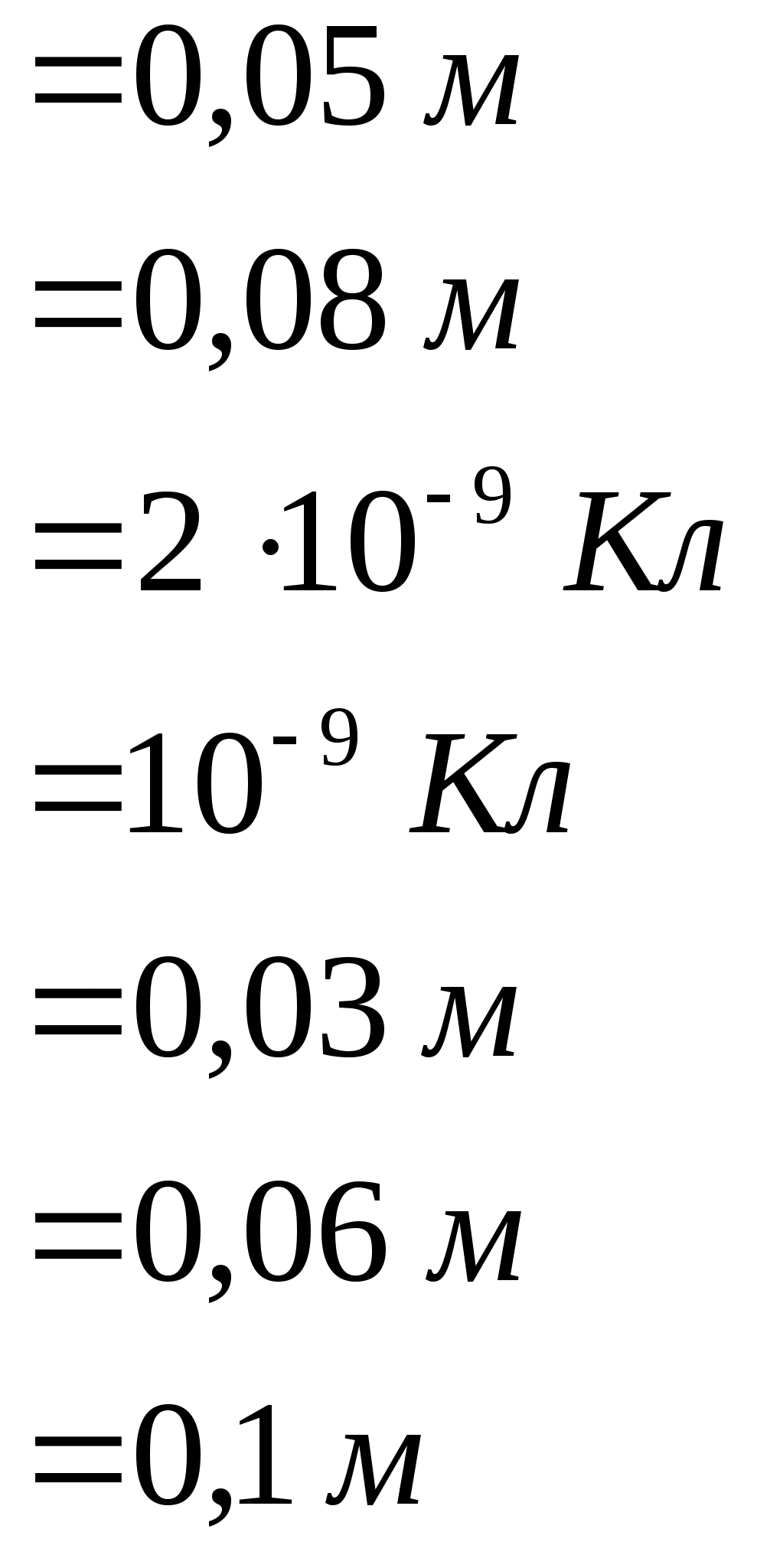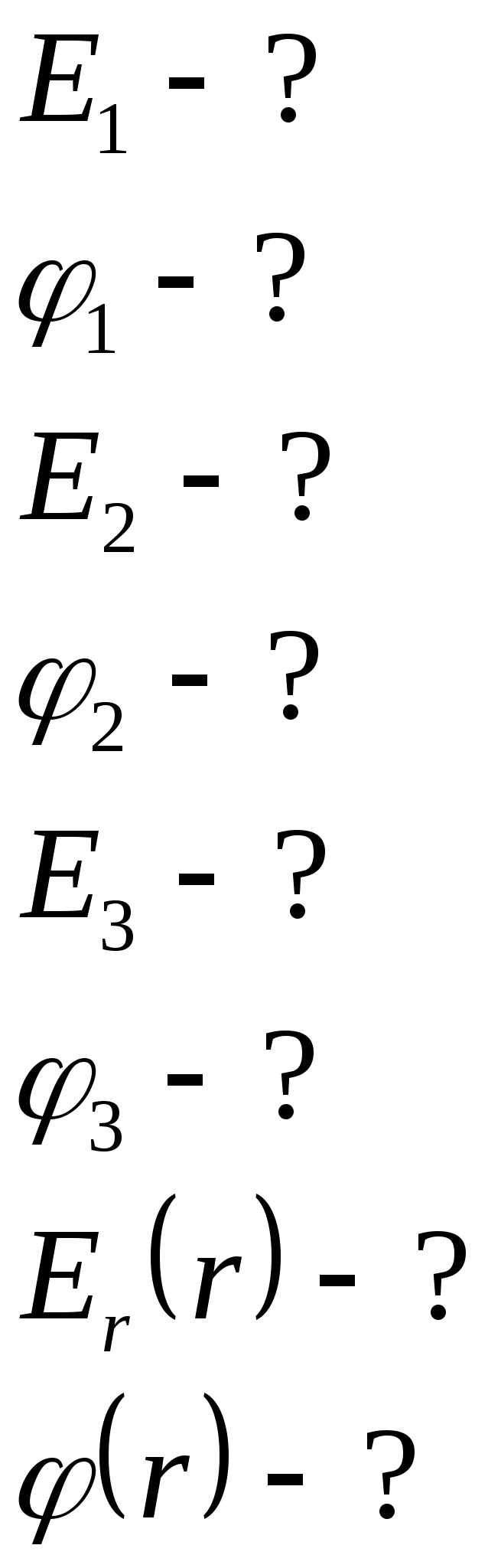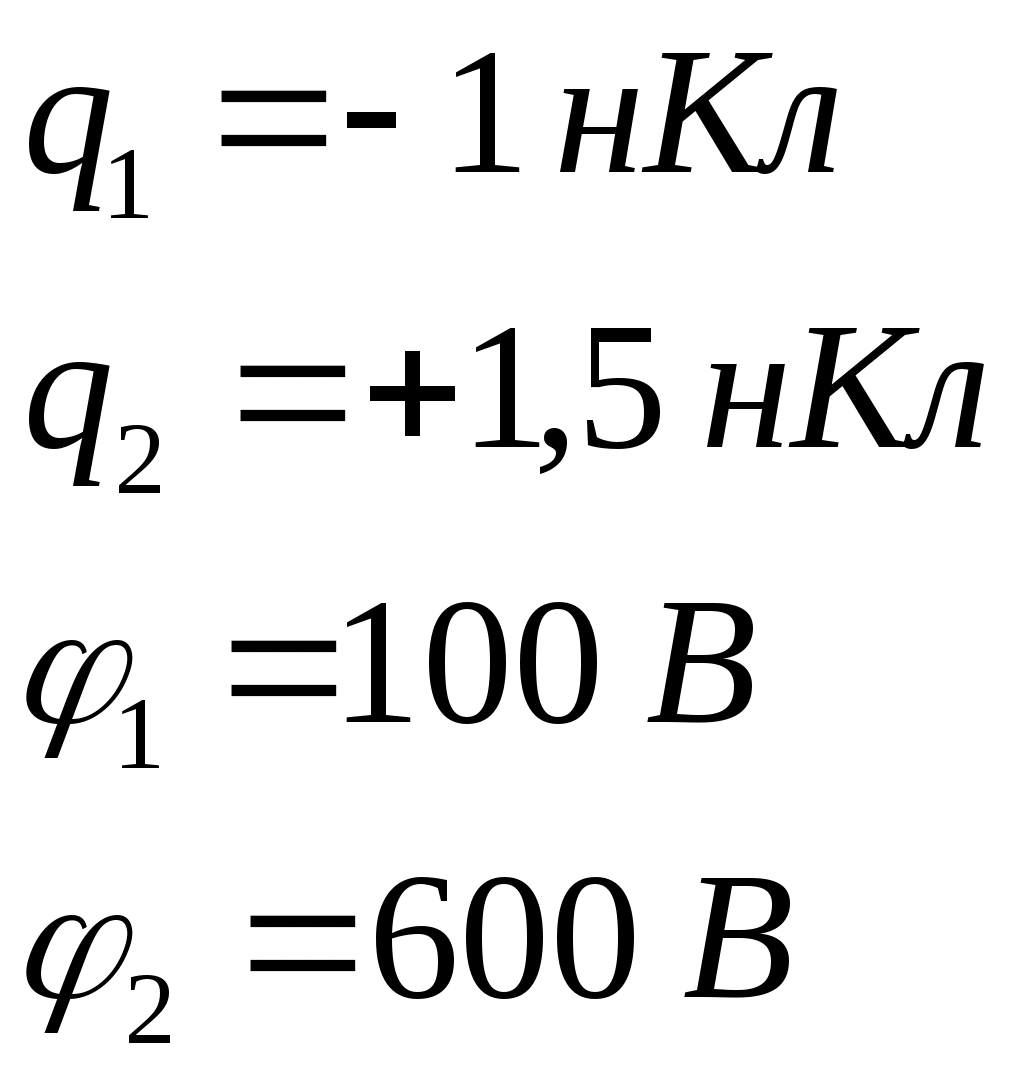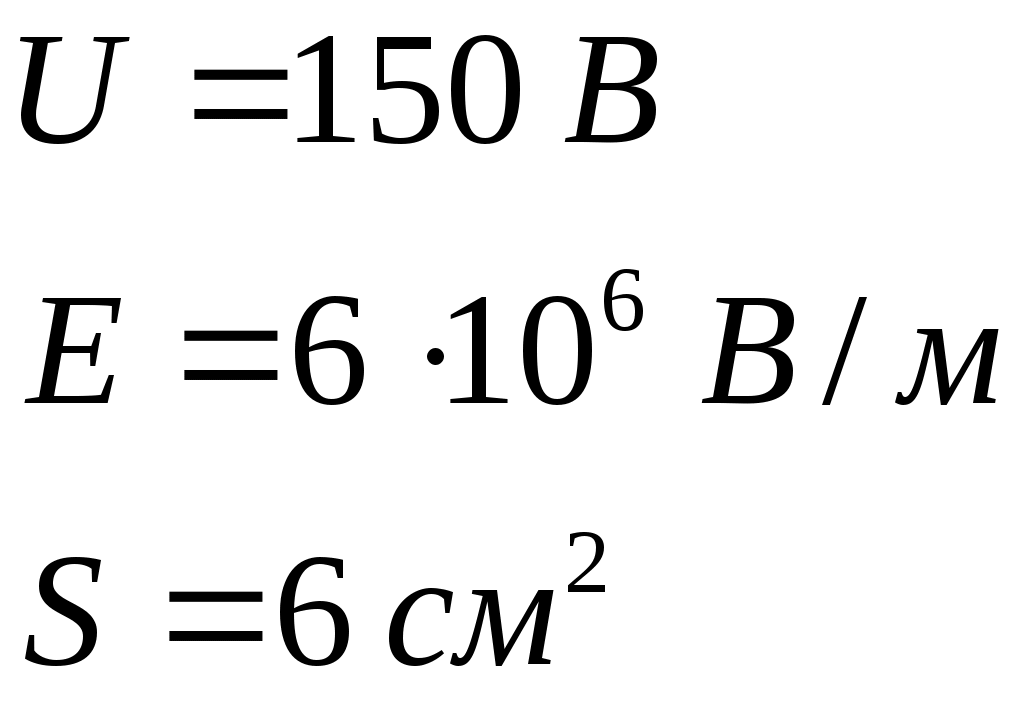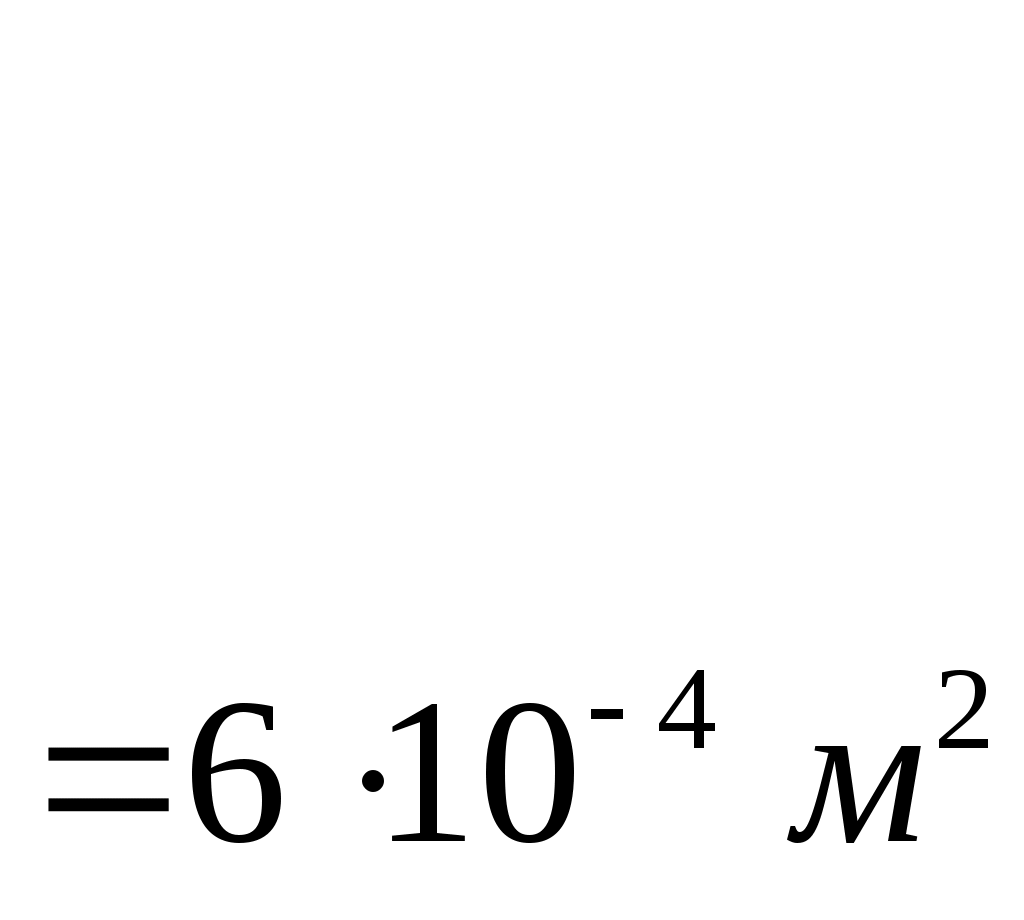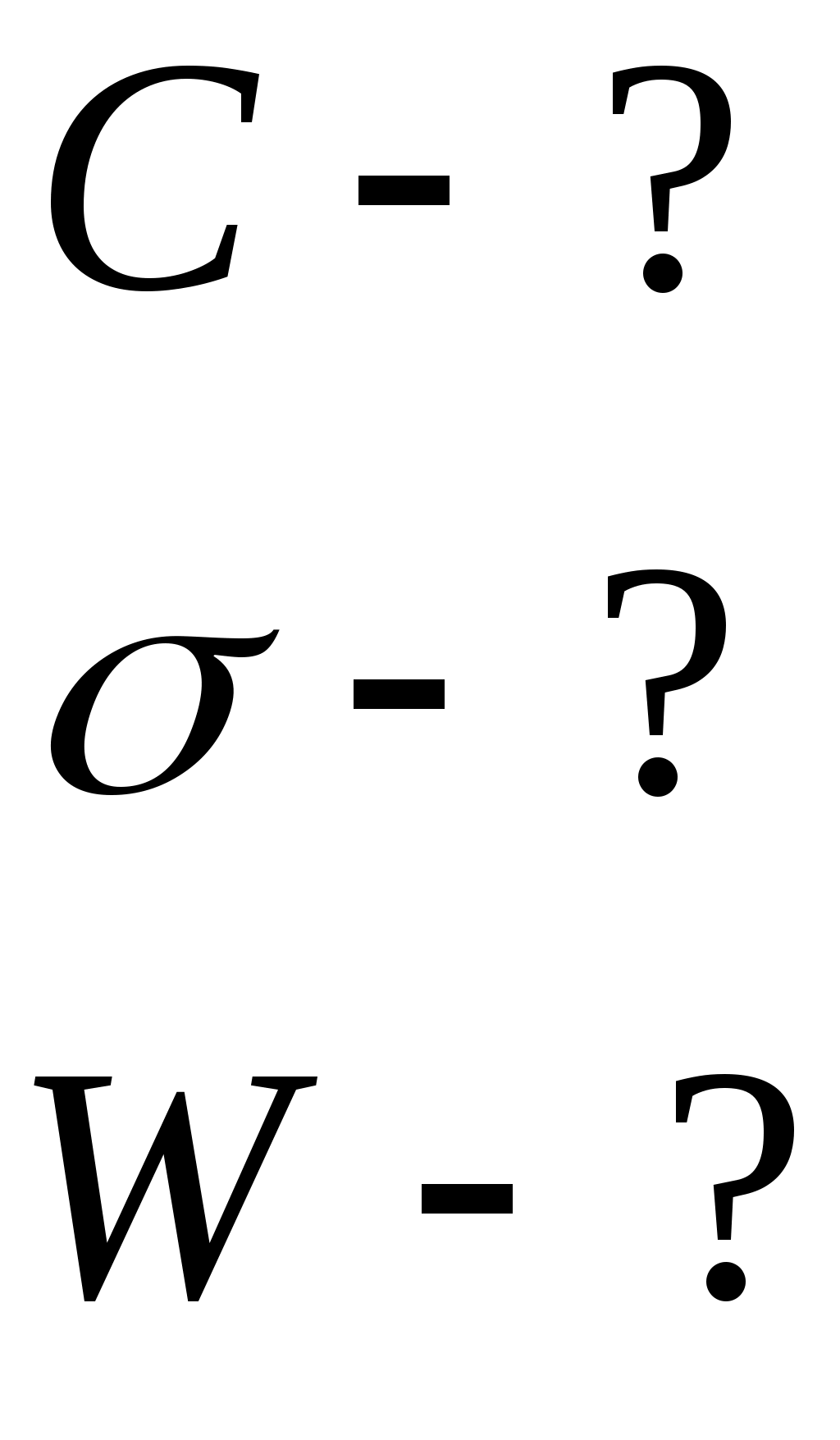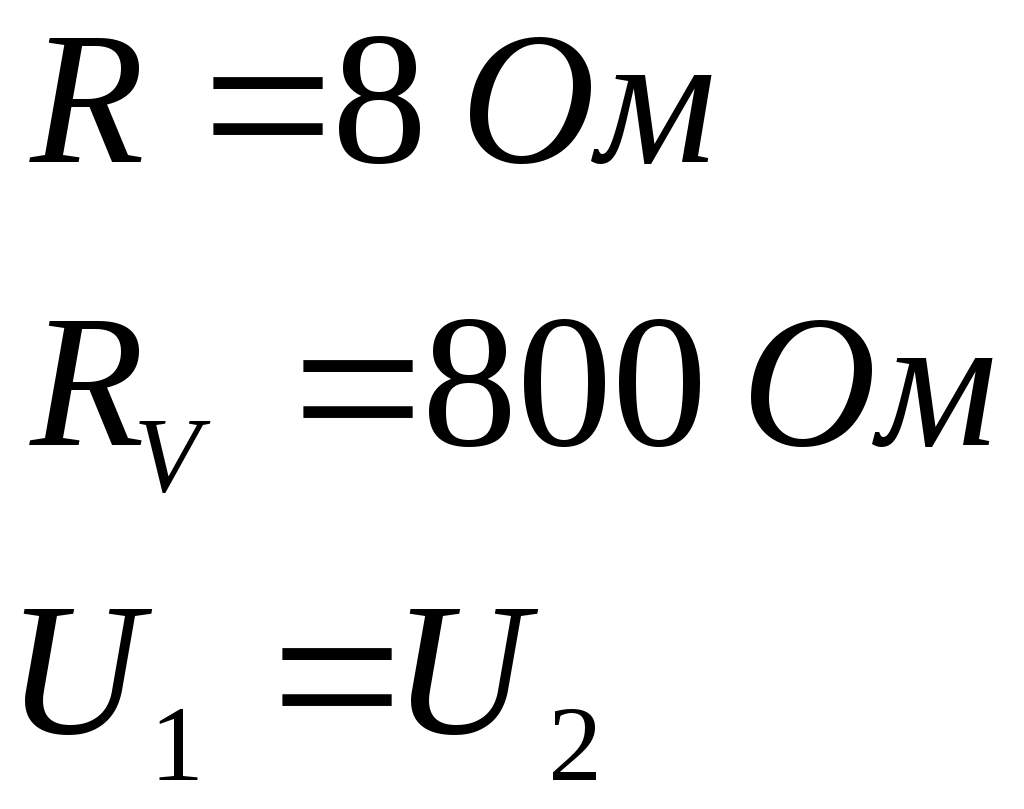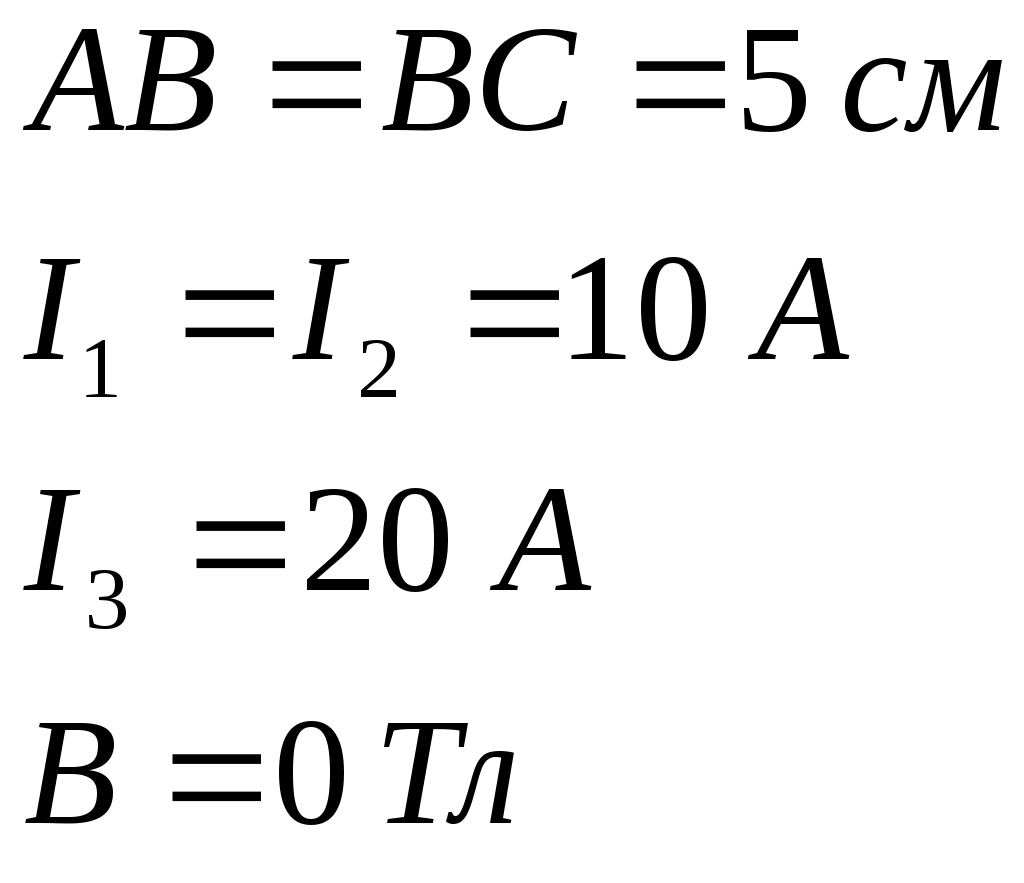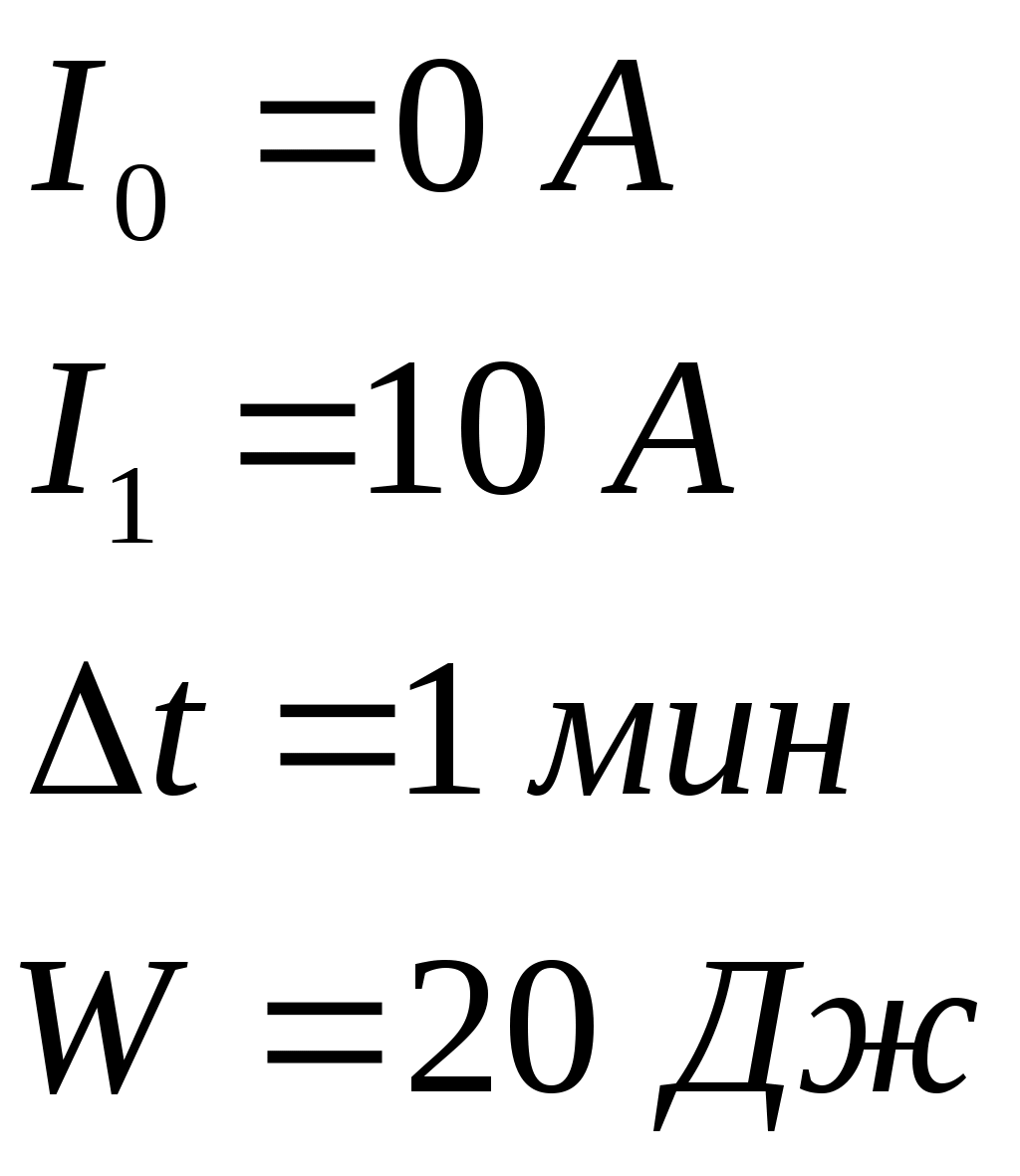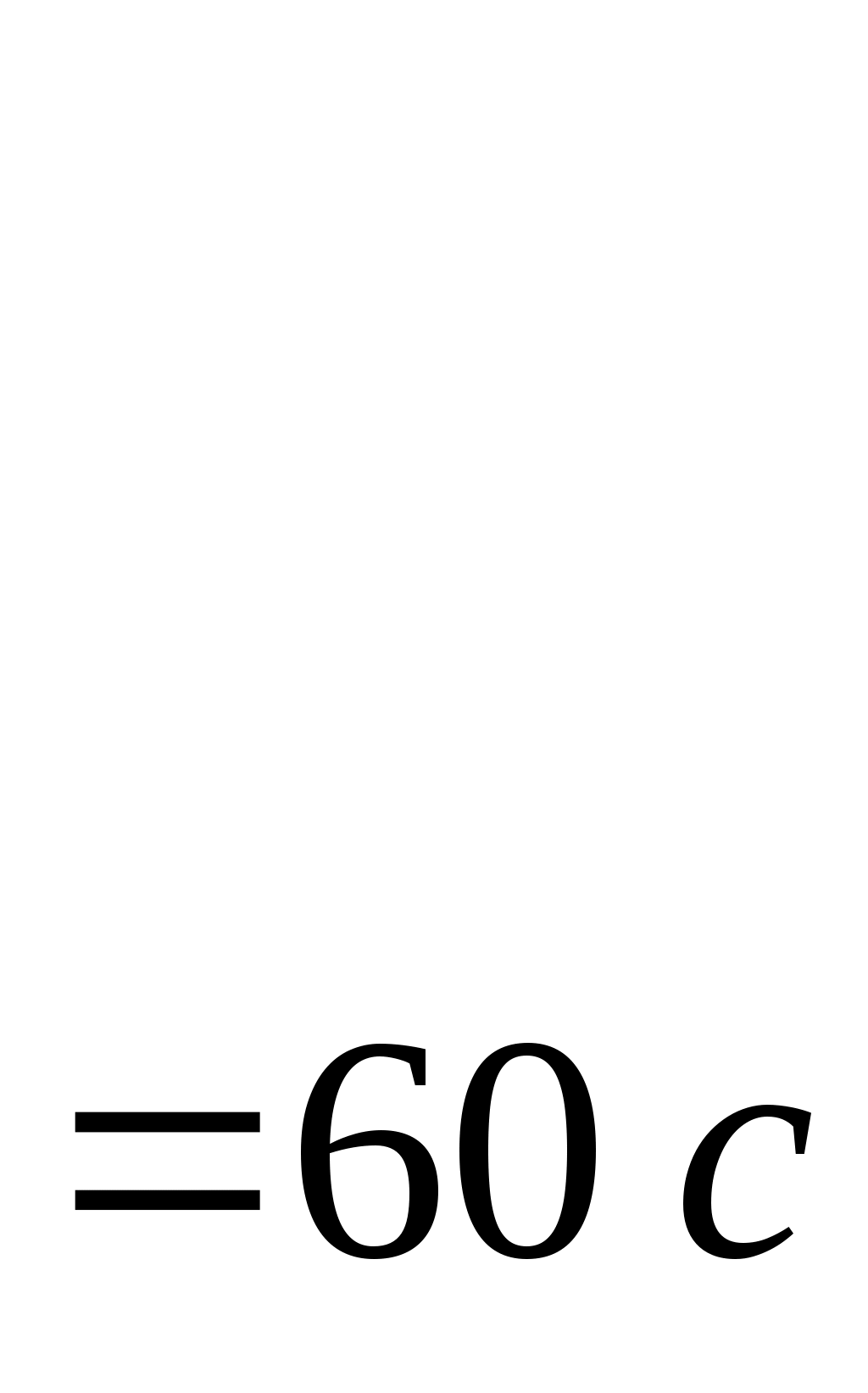основы геотехники. Вариант_№_14. электростатика. Постоянный ток. Магнетизм
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
|
Тема: Электростатика. Постоянный ток. Магнетизм. Вариант № 14 Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Омский государственный технический университет» Кафедра «Физика» ДОМАШНЕЕ ЗАДАНИЕ № 2 «ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК. МАГНЕТИЗМ» Вариант № 14 Выполнил: группа: Институт заочного обучения Проверил: _____________________ Омск Задача № 4 Два шарика массой по 0,2 г подвешены в общей точке на нитях длиной 0,5 м. Шарикам сообщили заряд и нити разошлись на угол 90°. Определить напряженность и потенциал поля в точке подвеса шариков.
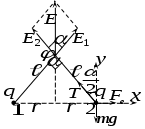 Пусть каждый из шариков несет на себе заряд величиною Согласно второму закону Ньютона: В проекции на координатные оси, получим: ось х: ось у: Получим: 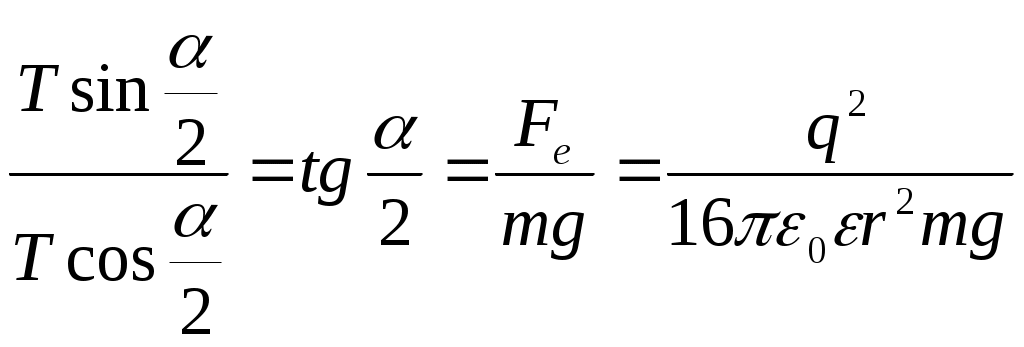 ; ;Согласно построению рисунка: Следовательно: 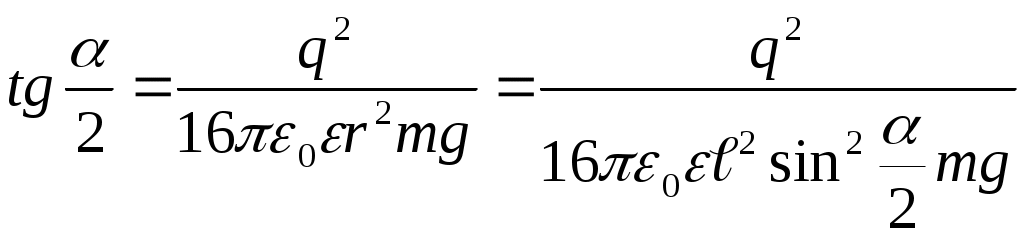 ; ;Заряд каждого из шариков: Напряженности полей зарядов в точке подвеса их нитей: 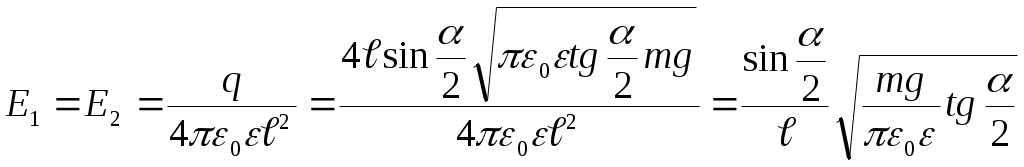 ; ;Согласно принципу суперпозиции, напряженность электростатического поля в рассматриваемой точке системы, будет равна: Поскольку 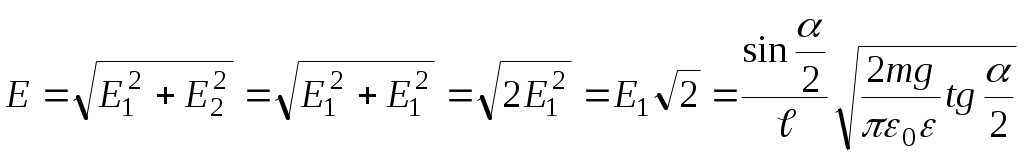 ; ;Потенциалы полей зарядов в точке подвеса их нитей: 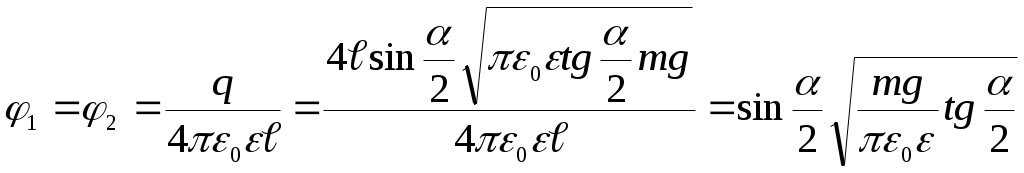 ; ;По принципу суперпозиции, потенциал результирующего поля: Проверка размерности: Результат расчета: 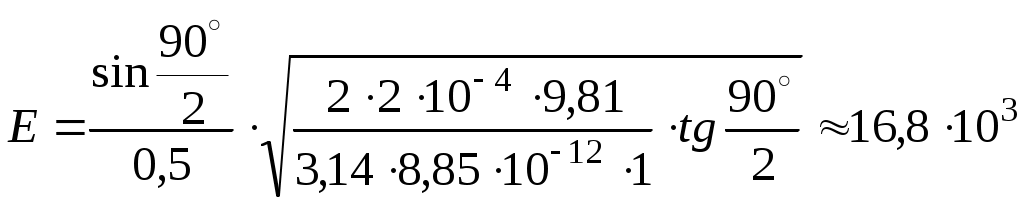 (В/м); (В/м);Ответ: 16,8 кВ/м; 11,9 кВ Задача № 15 Поле создано двумя равномерно заряженными концентрическими сферами радиусами
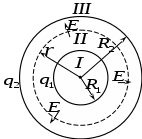 По теореме Остроградского-Гаусса: Выберем произвольным образом мнимую сферическую поверхность радиуса По определению потока, в данном случае, для потока напряженности электрического поля сквозь замкнутую мнимую сферическую поверхность, можно записать: Таким образом: Имеем: Для нахождения величины 1) область I ( В этом случае мнимая сферическая поверхность будет внутри внутренней сферы и охватываемый ею заряд будет равен нулю (весь заряд остался вне мнимой сферы): Таким образом: 2) область II ( В этом случае мнимая сферическая поверхность будет внутри внешней сферы, и будет полностью охватывать только внутреннюю сферу с ее зарядом, равным: Таким образом: 3) область III ( В этом случае мнимая сферическая поверхность будет полностью охватывать обе сферы с их суммарным зарядом, равным: Таким образом: Поскольку в области Определим потенциал поля в области Аналогичным образом, для потенциала поля в области Проверка размерности: Результат расчета: Поскольку при выводе формул мы не учитывали знаков зарядов сфер, то при подстановке их значений необходимо принимать во внимание и их знаки. 1) 2) 3) Построим графики зависимостей 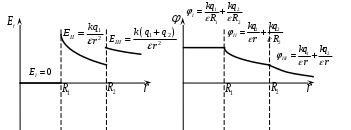 Ответ: 0 В/м, 472,5 В; 5 кВ/м, 412,5 В; 2700 В/м, 270 В Задача № 26 Заряд -1 нКл переместился в поле точечного заряда +1,5 нКл из точки с потенциалом 100 В в точку с потенциалом 600 В. Определить работу сил поля и минимальное расстояние между этими точками.
Работа по перемещению точечного заряда Поскольку заряд Пусть расстояние от заряда Можем записать: 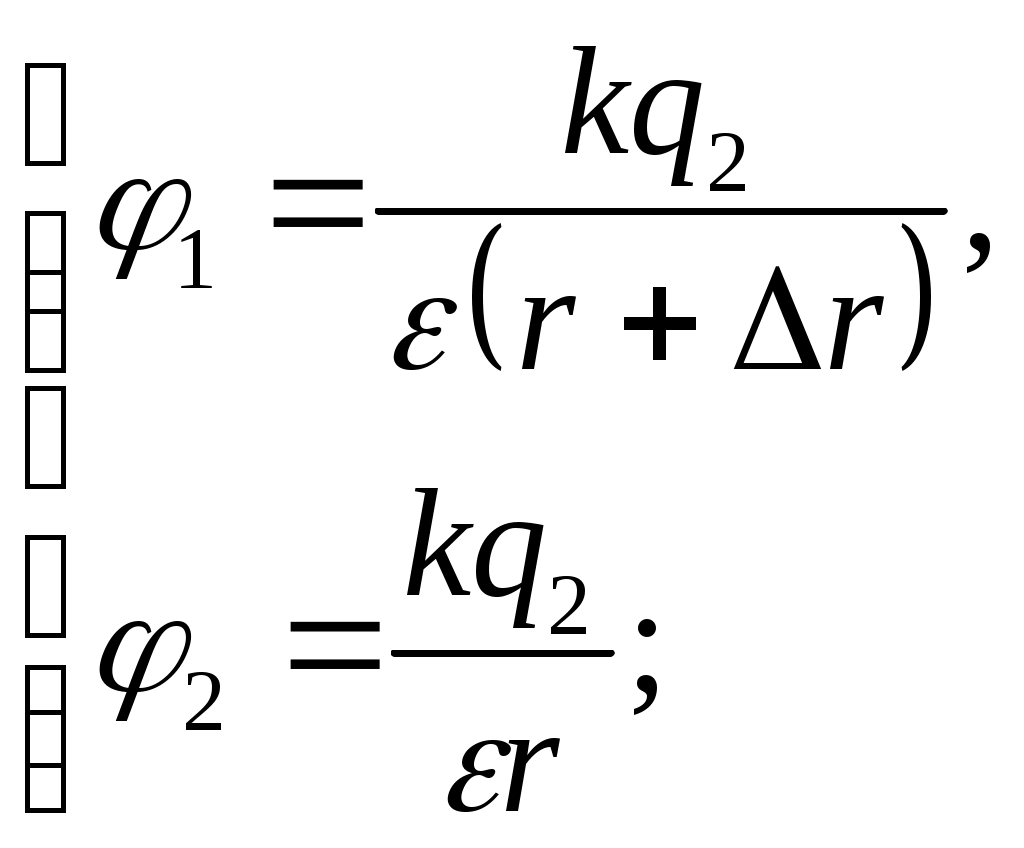 Поделим второе уравнение системы на первое, получим: Следовательно: Из выражения для Таким образом: Проверка размерности: Результат расчета: Ответ: 0,5 мкДж; 112,5 мм Задача № 37 Конденсатор с парафиновым диэлектриком заряжен до разности потенциалов 150 В. Напряженность поля 6·106В/м, площадь пластин 6 см2. Определить емкость конденсатора, поверхностную плотность заряда на обкладках и энергию конденсатора.
Электрическая емкость конденсатора: Имеем: Поскольку напряженность поля конденсатора Энергия заряженного конденсатора: Проверка размерности: Результат расчета: Ответ: 0,43 нФ; 0,11 мКл/м2; 4,78 мкДж Задача № 48 В цепь, состоящую из батареи и резистора сопротивлением
 Внешнее сопротивление цепи: 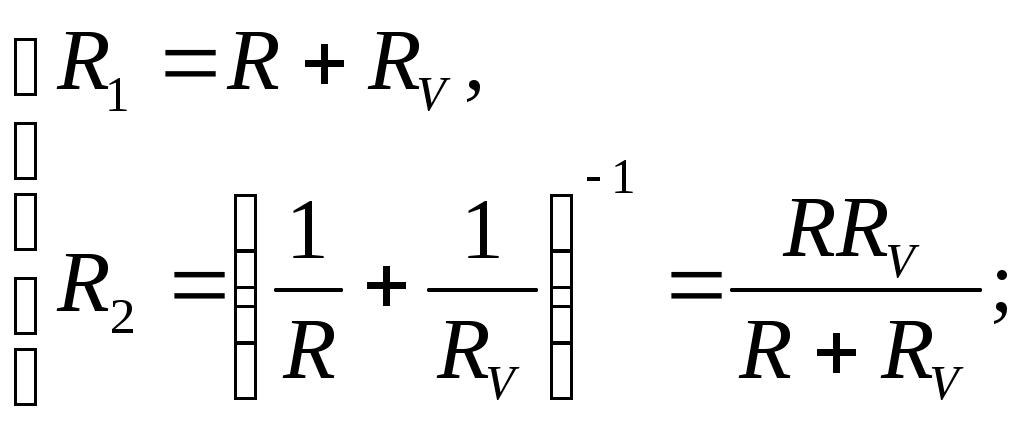 Согласно закону Ома для замкнутой электрической цепи, сила тока в ней: 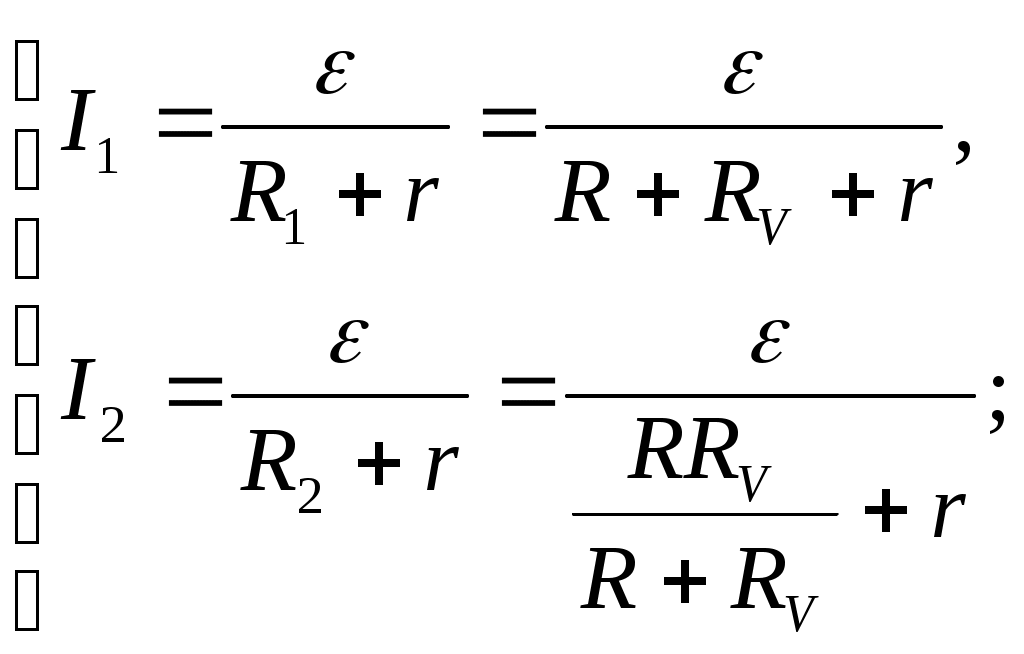 Пользуясь правилами последовательного и параллельного соединений элементов и законом Ома для однородного участка электрической цепи, для напряжения на вольтметре можем записать: 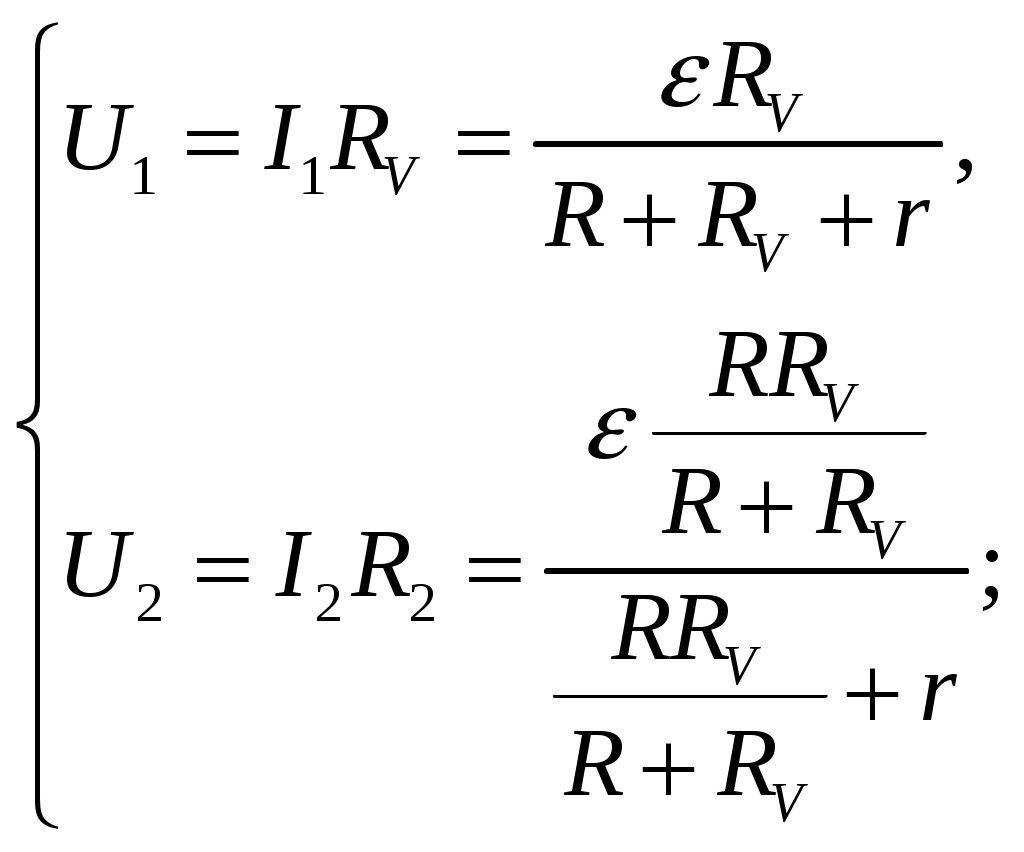 По условию задачи 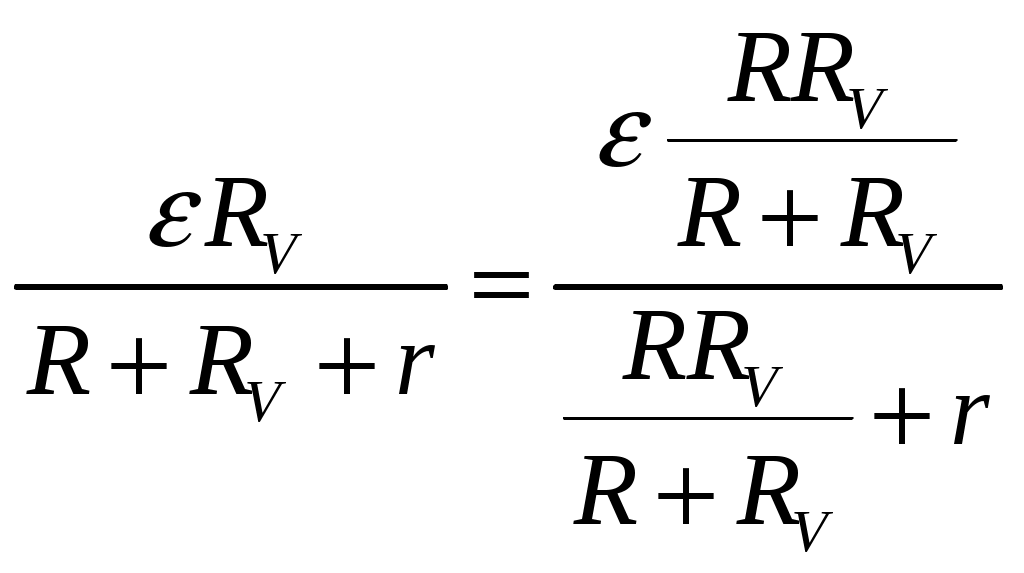 ; ;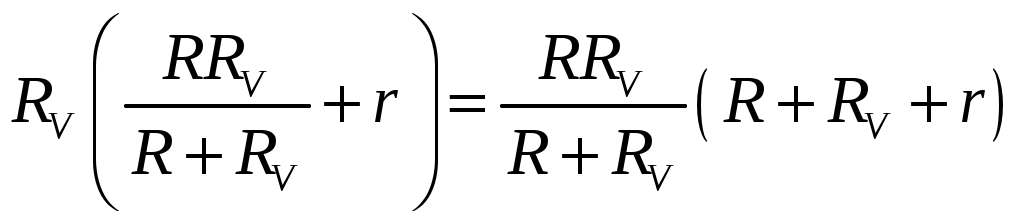 ; ;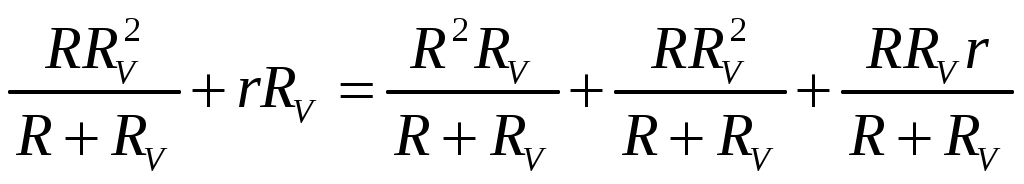 ; ;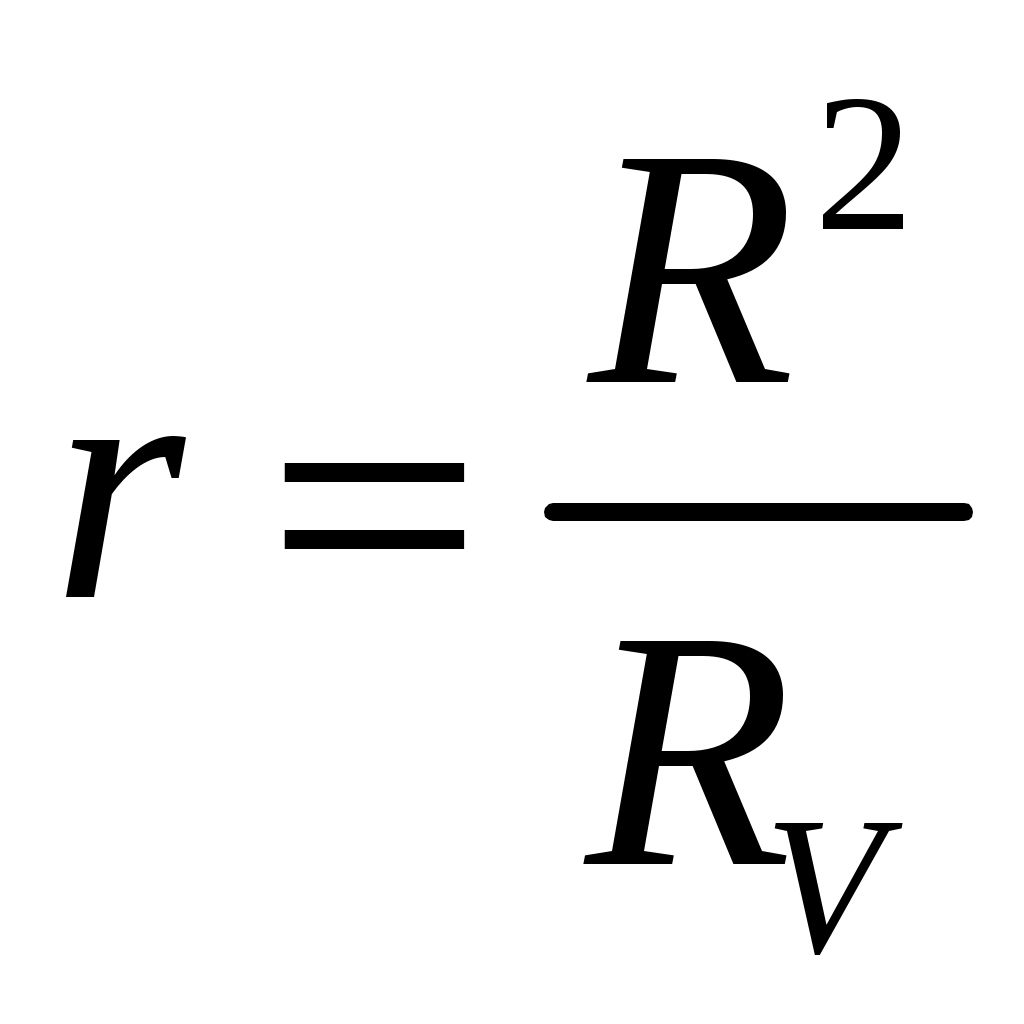 ; ;Проверка размерности: Результат расчета: 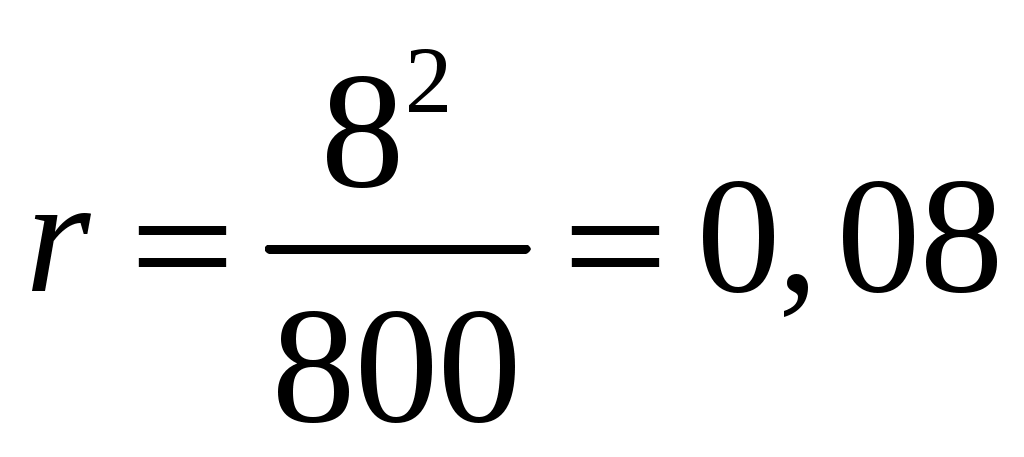 (Ом); (Ом);Ответ: 0,08 Ом Задача № 59 Какая мощность выделяется в единице объема медного проводника длиной
Исходя из закона Джоуля-Ленца, мощность тока в проводнике равна: Следовательно, мощность тока в единице объема проводника: 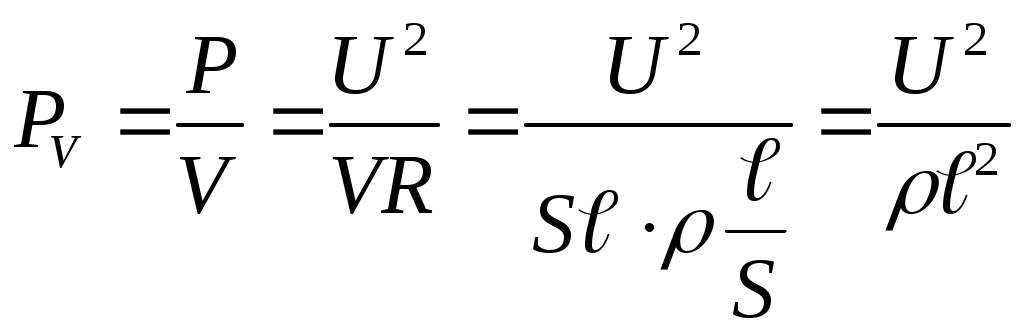 , где , где Проверка размерности: Результат расчета: Ответ: 23,5 ГВт Задача № 70 На рисунке изображены сечения трех прямолинейных бесконечно длинных проводников с токами. Расстояния
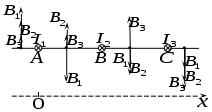 Будем искать в этой задаче расстояние Поскольку магнитное поле создается тремя токами, тогда его индуктивность, согласно принципу суперпозиции, будет равна: Исходя из построения рисунка, очевидно, что искомая точка пространства не может быть в областях до точки А либо после точки С. Рассмотрим все возможные варианты, при этом можем записать: 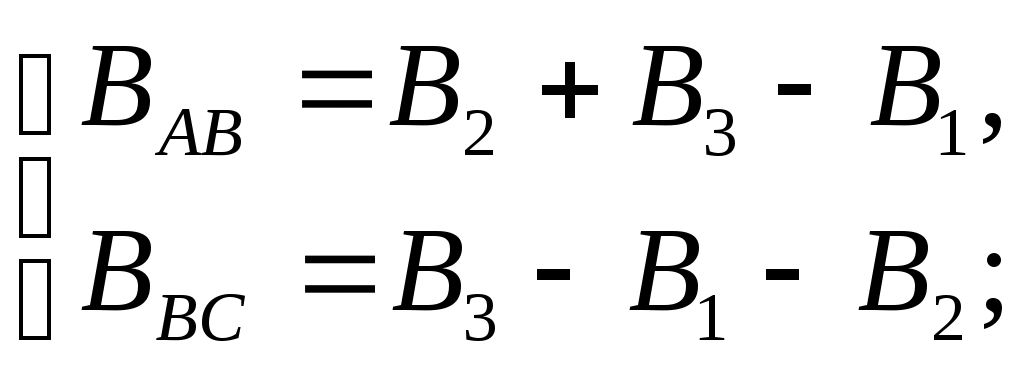 Поскольку токи текут по прямым бесконечно длинным проводам, тогда индукция их собственных магнитных полей будет определяться выражением: Таким образом: 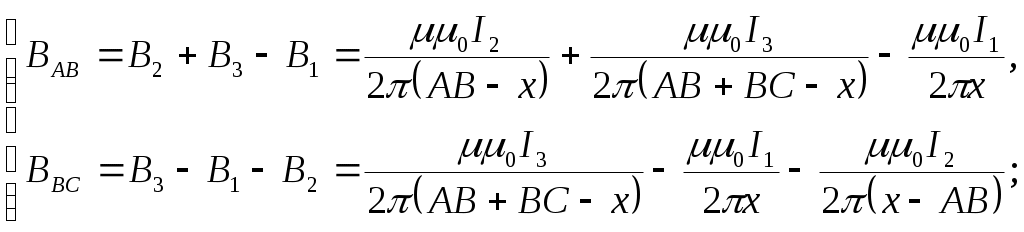 Поскольку индукция магнитного поля в искомой точке пространства должна равняться нулю (согласно условию задачи), тогда, рассматривая уравнения системы по отдельности друг от друга, получим: 1) область пространства Учитывая, что Получим квадратное уравнение: Дискриминант уравнения: Корни уравнения: 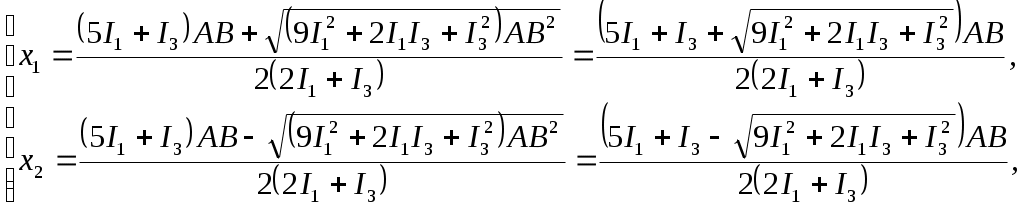 Проверка размерности: Результат расчета: 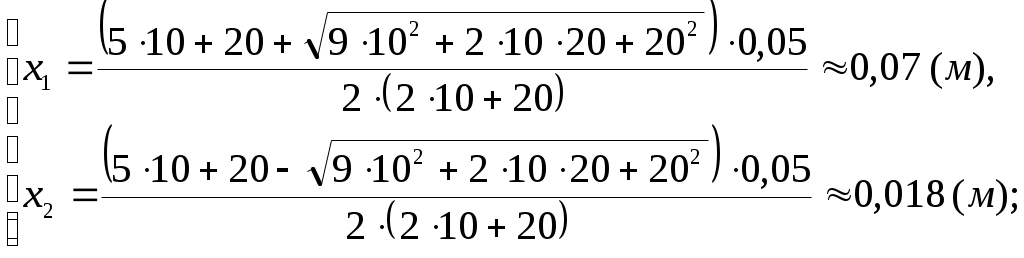 Поскольку 2) область пространства Учитывая, что Получим квадратное уравнение: Поскольку получили квадратное уравнение такое же, как и в предыдущем пункте, то и корни его будут Ответ: искомая точка поля находится на отрезке Задача № 93 Сила тока в соленоиде равномерно возрастает от 0 до 10 А за 1 мин, при этом соленоид накапливает энергию 20 Дж. Какая ЭДС индуцируется в соленоиде?
Согласно закону электромагнитной индукции: Энергия магнитного поля соленоида при конечном значении силы тока в нем: Индуктивность катушки: Поскольку сила тока в соленоиде возрастает равномерно, тогда в общем виде закон ее зависимости от времени должен быть следующим: Определим значения 1) в начальный момент времени 2) в конечный момент времени Таким образом, закон возрастания силы тока в контуре примет вид: В конечном итоге: 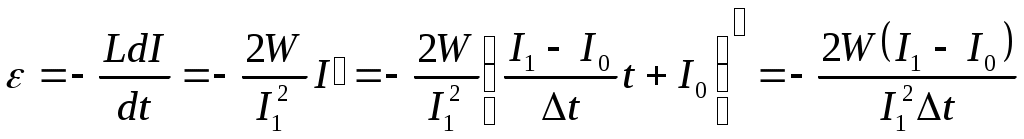 ; ;Проверка размерности: Результат расчета: Знак «-» в полученном результате объясняется правилом Ленца и в ответе мы его учитывать не будем. Ответ: 66,7 мВ Задача № 82 На концах крыльев самолета размахом 20 м, летящего со скоростью 900 км/ч, возникает электродвижущая сила индукции 0,06 В. Определить вертикальную составляющую напряженности магнитного поля Земли.
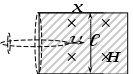 Двигаясь в магнитном поле Земли за некоторое время Поскольку в задаче идет речь о вертикальной составляющей магнитного поля Земли, тогда угол По закону электромагнитной индукции, имеем: В полученном выражении знак «-» объясняется правилом Ленца и в дальнейшем мы его учитывать не будем. В конечном итоге: Проверка размерности: Результат расчета: Ответ: 9,6 А/м Задача № 71 Незакрепленный проводник массой 0,1 г и длиной 7,6 см находится в равновесии в горизонтальном магнитном поле напряженностью 10 А/м. Определить силу тока в проводнике, если он перпендикулярен линиям индукции поля.
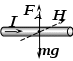 Как известно, на проводник с током в магнитном поле действует сила Ампера: Согласно условию и исходя из построения рисунка, можем записать: Таким образом: В конечном итоге: Проверка размерности: Результат расчета: Ответ: 1,03 кА |