курсовая 11.01.22. Электросвязь

• Название: Электросвязь
• Дата: 19.01.2022
• Размер: 174.42 Kb.
• Имя файла: курсовая 11.01.22.docx
• Тип: Документы; #336263

ВВЕДЕНИЕ
Электросвязь - это совокупность человеческой деятельности , главным образом технической , связанной с передачей сообщений на расстояние с помощью электрических сигналов. Непрерывное развитие народного хозяйства и культуры приводит к интенсивному росту передаваемой информации, поэтому значение электросвязи в современной технике и в современной жизни огромно. Уже в настоящее время хорошо развитая сеть электросвязи облегчает управление государством. В будущем , когда методы управления с помощью ЭВМ будут преобладающими , наличие хорошо развитой сети электросвязи будет обусловливать управление государством.

В системах передачи сообщений используются как аналоговые , так и цифровые сигналы. В настоящее время широко применяются цифровые системы передачи. Так как они обладают более высокой помехоустойчивостью, что позволяет передавать на более далекие расстояния. Так же цифровые системы передачи в аппаратуре преобразования сигналов используют современную элементарную базу цифровой вычислительной технике и микропроцессоров. Поэтому аналоговый сигнал преобразуется в цифровой сигнал и в таком виде передается по линии связи; на приемной стороне происходит обратный процесс - преобразование цифрового сигнала в аналоговый.

В данной курсовой работе необходимо рассчитать технические характеристики цифровой системы связи.

Рассчитать основные характеристики системы передачи сообщений (рис.1), включающий в себя источник сообщений (ИС), дискретизатор (Д), кодирующее устройство (Кодер), модулятор (Мод), линия связи, демодулятор (Дем), декодер (Дек) и фильтр-восстановитель (ФВ).


Рис.1. Структурная схемацифровой системы передачи сообщений
Исходные данные

амин(В)	амакс(В)	Fc(Гц )	j	Вид моду-ляции	Кпк	N0 (Bт/Гц)	Способ приёма
0	+6,4	4∙106	55	ФМ	0,5	2,5 ∙10-11	когерентный

Источник сообщений

Источник сообщений выдает сообщение а(t), представляющее собой непрерывный стационарный случайный процесс, мгновенные значения которого в интервале а min a max распределены равномерно, а мощность сосредоточена в полосе частот от 0 до Fc.

Требуется:

1. Записать аналитические выражения и построить график одномерной плотности вероятности мгновенных значений сообщения а(t).

2. Рассчитать значения математического ожидания ma и дисперсии сообщения а(t).

Вычисления.

1) Из условия нормировки для достоверного события имеем: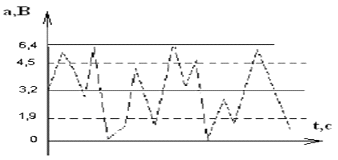


= 0,15625

)
amin = 0 B, amax = 6,4 B, = 4,5 В, = 1,9 В, .
3) Математическое ожидание (МО) определяет среднее значение случайной величины



Дисперсия характеризует разброс случайной величины относительно ее среднего значения (физический смысл - средняя мощность отклонения от некоторой средней величины)



Величину называют стандартным или среднеквадратическим отклонением (СКО).

σа= 1,3606 В

Дискретизатор

Передача непрерывного процесса осуществляется дискретными методами. Для этого сообщение а(t) дискретизируется по времени и квантуется по уровню с равномерным шагом. Шаг квантования по уровню а= 0,1В.

Требуется:

1. Определить максимально допустимый интервал дискретизации по времени (t).

2. Определить число уровней квантования (L).

. Рассчитать среднюю мощность шума квантования.

. Рассматривая дискретизатор как источник дискретных сообщений с объемом алфавита L, определить его энтропию Н(А)и производительность Η'(А)при условии, что отсчеты, взятые через интервал Δt, статистически независимы.

Вычисления.

1) По теореме Котельникова, в полосе частот [0 , Fc] Гц шаг дискретизации по времени;


.

2) Число уровней квантования L при равномерном шаге определяется как частное от деления размаха сигнала на шаг квантования а. Число уровней квантования L равно:

) Поскольку квантование по уровню производится с равномерным шагом, то закон распределения шума квантования также будет равномерным, и не будет зависеть от номера интервала квантования. Тогда на интервале

Cредняя мощность (дисперсия шума квантования):

) Энтропия - это средняя информативность источника на один символ, определяющая ‘неожиданность’ или ‘непредсказуемость’ выдаваемых им сообщений. Для источника, не обладающего памятью с алфавитом А энтропия записывается следующим образом:


Где L - объем алфавита , , i=1,2,3,…,L-вероятности выдачи источником символов , причем они не зависят от номера элемента последовательности, т.к. источник является стационарным.

Т.к. p(a1)= p(a2)=…= p(ai), то

Следовательно, энтропия равна:
бит/символ
Если источник сообщения имеет фиксированную скорость символ/с, то производительность источника можно определить, как энтропию в единицу времени, (секунду):

Кодер

Кодирование осуществляется в два этапа.

Первый этап:

Производится примитивное кодирование каждого уровня квантованного сообщения k- разрядным двоичным кодом.

Второй этап:

К полученной k- разрядной двоичной кодовой комбинации добавляется один проверочный символ, формируемый простым суммированием по модулю 2 всех информационных символов (код (n, n-1) с одной проверкой на четность).

В результате этих преобразований на выходе кодера образуется синхронная двоичная случайная последовательность b(t) (синхронный случайный телеграфный сигнал), состоящая из последовательности биполярных импульсов единичной высоты, причем положительные импульсы в ней соответствуют символу «0», а отрицательные - символу «1» кодовой комбинации.

Требуется:

1. Определить число разрядов примитивного кода k, необходимое для кодирования всехL уровней квантованного сообщения.

2. Найти избыточность ρk кода с одной проверкой на четность.

. Записать двоичную кодовую комбинацию, соответствующую передачеj-го уровня, считая, что она представляет собой запись числа jв двоичной системе счисления.

. Записать соответствующую комбинацию кода с проверкой на четность, указать в ней информационные и проверочный разряды

. Определить число двоичных символов, выдаваемых кодером в секунду (скорость манипуляции) Vк и длительность передачи символа (тактовый интервал синхронного двоичного сигнала) Т.

Вычисления.

1) Для кодирования L =64 уровней квантованного сообщения число разрядов двоичной кодовой комбинации:


n=k+1=7
) Определим избыточность кода.
0,1428
) j = 55. В двоичном виде



1 0 1 1 1



b10 b9 b7 b6 b5 b3

) Определим проверочные символы (они располагаются на 1,2,4,8 позициях):

b1= b3 b5 b7 b9 r1=b1 b3 b5 b7 b9 b10= b3 b6 b7 b10 r2= b2 b3 b6 b7 b10= b5 b6 b7 r3= b4 b5 b6 b7=b9 b10 r4=b8 b9 b10

проверочный разряд а7 = а6+ а5+ а4+ а3+ а2+ а1=1

В результате получаем кодовую комбинацию:1110111;

) Число двоичных символовVк , выдаваемых кодером в единицу времени, определяется числом отсчетов в секунду ( ) и числом двоичных символов, приходящихся на один отсчет:
Vn= n/∆t= 7/0,125·10-6 = 56·106 бит/с;
Длительность T двоичного символа определяется как:
T= 1/Vn = 0, 0178∙10-6 с = 17, 8∙10-9 с
Модулятор

В модуляторе синхронная двоичная случайная последовательность биполярных импульсов b(t) осуществляет модуляцию гармонического переносчика Um = cos(2πft). (Um=1В, f = 100 Vn Гц)

Фазовая модуляция (ФМ).
«0» - U0(t) = Umcos2πft;

«1» - U1(t) = -Um cos2πft.
Требуется:

1. Записать аналитическое выражение модулированного сигнала u(t) связывающее его с первичным сигналом b(t).

2. Построить графики временных диаграмм первичного сигнала b(t),представляющего кодовую комбинацию j -го уровня сообщения (bk+1, bk, bk-1,… b1),и соответствующего модулированного сигнала u(t)(с учетом заданного вида модуляции).

. Записать аналитическое выражение и построить график корреляционной функции первичного (модулирующего) сигнала Вb(τ).

4. Записать аналитическое выражение и построить график спектральной плотности мощности (энергетического спектра) этого сигнала Gb(f)

. Определить ширину ΔFbуказанного энергетического спектра Gb(f)поупрощенному правилу, согласно которому учитывается ширина главного (центрального) лепестка спектра. Полученное значение ΔFbотложить на спектральной диаграмме Gb(f).

. Записать аналитическое выражение и построить график энергетического спектра модулированного сигнала Gu(f) (для сигналов ЧМ значение девиации частоты Δfвыбрать таким, чтобы обеспечивалась ортогональность элементов сигнала U0(t)и U1(t)на интервале Т).

7. Определить полосу частот (ширину энергетического спектра) модулированного сигнала ΔFU.Отложить полученное ее значение на диаграмме спектра Gu(f).

Вычисления.

1) Аналитическое выражение для ФМ модулированного сигнала:
f0 = 100·Vn = 56·108 Гц

U0(t) = cos(2πf0 t)= cos(

U1(t) = cos(2πf0 t+π)= - cos
Получим:

2) Временные диаграммы модулирующего b(t) и модулированного U(t) сигналов, соответствующие передачи j-го уровня сообщения a(t).

) , где T длительность импульсов.
График корреляционной функции модулирующего сигнала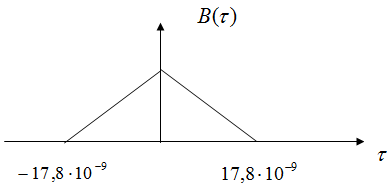


) Спектральная плотность величины - предел отношения величины (напряжения, мощности и др.), соответствующей узкому участку оптического спектра, к ширине этого участка.

Спектральная плотность мощности модулирующего сигнала Gb(f):






=2πf,


График спектральной плотности мощности модулирующего сигнала GВ(f):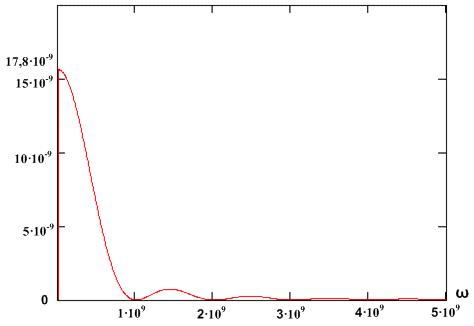


) На графике видно, что вся энергия модулирующего сигнала сосредоточена в полосе ∆Fb Гц.
f0 = 100·Vn = 56·108 Гц;

∆f=2/T=2/17,8·10-9 = 112 ,4·106 Гц;

∆ =57,124·108 Гц; -∆ =54,876·108 Гц.

)
График спектральной плотности мощности модулированного сигнала Gu(f):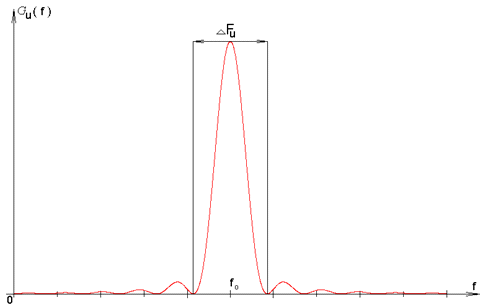


) Ширина энергетического спектра при ФМ будет в два раза больше ширины энергетического спектра модулирующего сигнала.

Канал связи

Передача сигнала u(t) осуществляется по каналу с постоянными параметрами и аддитивным флуктуационным шумом n(t) с равномерным энергетическим спектром N0/2 (белый шум).

Сигнал на выходе такого канала можно записать следующем образом:
z(t) = s(t)+ n(t),
где s(t) = u(t)∙Кпк - полезный сигнал, n(t)- аддитивная помеха

Требуется:

1. Записать аналитическое выражение, связывающее входной и выходной сигналы в заданном канале с учетом аддитивного шума.

2. Найти мощность шума на выходе канала Ршвполосе частот модулированного сигнала ΔFU.

3. Найти мощность модулированного сигнала на входе демодулятора Рs(для АМ соответствующего уровню «1»).

4. Найти отношение сигнал - шум Рs / Рш

5. Определить пропускную способность канала С;

. Рассчитать эффективность использования пропускной способности канала Кс, определив ее как отношение производительности источника сообщений Η'(А)к пропускной способности канала С.

Вычисления.

2) Зная спектральную плотность мощности N0 можно определить мощность шума Рш в полосе ∆Fu (промодулированного сигнала).
Вт.
) Мощность модулированного сигнала: Р = = 0,01 Вт

)

) Под пропускной способностью понимают количество, данных которое может быть передано по каналу за 1 секунду.
С = ∆FU·log2(1+Pc/PШ)

С = 112∙106·log2(1+7,142) = 343,056 ∙106 бит/с
) Эффективность использования пропускной способности канала Кс определяется как отношение производительности источника Н’ к пропускной способности канала С.
Кс=
Демодулятор

В демодуляторе осуществляется оптимальная когерентная или некогерентная (в зависимости от варианта) обработка принимаемого сигнала z(t) = u(t) + n(t)

Требуется:

1. Изобразить структурную схему оптимального демодулятора для заданного вида модуляции и способа приема.

2. Рассчитать среднюю вероятность ошибочного приема двоичного символа рош.

. Определить, как нужно изменить энергию сигнала, чтобы при других видах модуляции и заданном способе приема обеспечить найденное значение вероятности ошибки рош.

Вычисления.
1)


Для фазовой модуляции Е0/2 = Е1/2, U1 = -U0, следовательно:




сообщение модулятор декодер связь


2) Вероятность ошибки рш оптимального когерентного демодулятора для канала с аддитивным нормальным белым шумом при передаче двоичных сообщений вычисляется следующим выражением:
рш = 1/2 (1-Ф(х));
Ф(х) - функция Крампа или интеграл вероятностей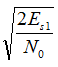
=

Es1 = Рs1 Т ;

0,0005
) При когерентном приёме вероятность ошибки при АМ, ЧМ, ФМ определяется соотношением , которое зависит от x. х- определяется из энергии сигнала, значит энергию измерять не надо, т.к. при других видах модуляции вероятность ошибки остаётся той же. ФМ обеспечивает наибольшую помехоустойчивость. Энергетический выигрыш её составляет в четыре раза по сравнению с АМ и в два раза по сравнению с ЧМ.

Декодер

В декодере декодирование осуществляется в два этапа. На первом этапе производится обнаружение ошибок в кодовой комбинации. Если ошибки не обнаружены, то на втором этапе из нее выделяются информационные символы, а затем k - разрядная двоичная кодовая комбинация преобразуется в элемент квантованного сообщения.

Требуется:

1. Оценить обнаруживающую способность q0заданного кода (n, n-1) с одной проверкой на четность.

2. Записать алгоритм обнаружения ошибок.

. Рассчитать вероятность необнаруженной ошибки рно.

Вычисления.

1) dmin = 2;

Наш код исправляет одну ошибку и обнаруживает

q = dmin-1 = 1ошибка

) Кодовая последовательность: 11111110

Если b9 = то, ошибки нет.

Если b9 ≠ то, ошибка есть.

. Вероятность не обнаружения ошибки определяется по формуле:

n - число разрядов, n= 7

q- обнаруживающая способность кода , q= 1; α = 2

р - вероятность ошибки в одном разряде, p = 0,0005


1,745∙10-6
Фильтр - восстановитель

Фильтр-восстановитель представляет собой фильтр нижних частот с частотой среза Fc.

Требуется:

1. Указать значение Fcрфильтра-восстановителя, при котором обеспечивается теоретически точное восстановление непрерывного сообщения.

2. Изобразить АЧХ и ФЧХ фильтра - восстановителя.

. Найти импульсную характеристику g(t) фильтра - восстановителя и начертить ее график.

Вычисления.

1) Частота среза связана со временем дискретизации . Из теоремы Котельникова:

Fc = 4∙106 Гц;
wср= =2·3,14·4∙106 = 25,12·106
2) Идеальная АЧХ фильтра - восстановителя описывается системой:
, где .
АЧХ имеет вид: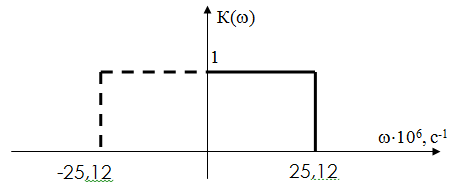



Рис. Идеальная АЧХ фильтра - восстановителя
Идеальная ФЧХ описывается уравнением 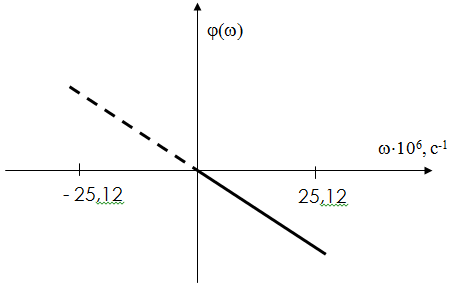, где − время задержки (маленькая величина порядка 10-4 − 10-5 с) и имеет вид:


Рис. Идеальная ФЧХ фильтра - восстановителя
3)



Вывод
В ходе данного проекта были приобретены навыки расчета основных характеристик системы передачи сообщений, включающей в себя источник сообщений, дискретизатор, кодирующее устройство, модулятор, линия связи, демодулятор, декодер и фильтр-восстановитель. Также уяснили, что наименее помехоустойчивый тип модуляции - амплитудный, а наиболее помехоустойчивый - фазовый.
Используемая литература:

1. 
   Теория электрической связи. Учебник для вузов. Под редакцией Кловского Д.Д. - М.: Радио и связь, 1999. - 433 с.
   

2. Нефедов В.И. Основы радиоэлектроники и связи. Учебник для вузов. - М.: Высшая школа, 2002. - 510 с.

3. Левченко В.И. Теория электрической связи. Курс лекций. ОмГТУ. 2009