Электротехниканаука, изучающая вопросы технического использования электромагнитных явлений для нужд промышленного производства и быта
 Скачать 401.25 Kb. Скачать 401.25 Kb.
|
 В Электротехника-наука, изучающая вопросы технического использования электромагнитных явлений для нужд промышленного производства и быта. Эта наука охватывает все электрические и магнитные явления, связанные с законами природы и научными законами. Особое значение имеет производство электрической энергии и её преобразование в другой вид энергии: механическую, тепловую, химическую и другую. Электрическая энергия применяется практически во всех областях деятельности современного общества. Энергия – это общая количественная мера различных форм движения материй. Различают различные формы проявления энергии: электрическая, тепловая, механическая, атомная, световая, электромагнитная. Возрастающая роль электрической энергии обеспечивается благодаря её свойствам: большому разнообразию технических средств получения электроэнергии, удобство передачи электроэнергии на большие расстояния и распределение её между потребителями. Для любого вида энергии можно назвать материальный объект, который является его носителем. Энергию относительно не сложно передавать на большие расстояния и легко преобразовывать в другие виды. Формы энергии в электронике: энергия неподвижных зарядов, энергия движущихся зарядов, электромагнитная. Её замечательные свойства находят ещё большее применение при использовании новой – ядерной – энергии. Электротехника развивается так стремительно, что сегодняшний высокий уровень её развития, завтра может оказаться недостаточным. Предмет ТОЭ опирается на курсы физики, математики, и включает изучение принципов устройств приборов, машин, аппаратов, использующих электромагнитную энергию, а также соотношения между электрическими и магнитными величинами. Большое значение электротехники во всех областях деятельности человека объясняется преимуществами электрической энергии перед другими видами энергии, а именно: электрическую энергию легко преобразовать в другие виды энергии (механическую, тепловую, световую, химическую и др.), и наоборот, в электрическую энергию легко преобразуются любые другие виды энергии; электрическую энергию можно передавать практически на любые расстояния. Это дает возможность строить электростанции в местах, где имеются природные ресурсы, и передавать электрическую энергию в места, где расположены источники промышленного сырья, но нет местной энергетической базы; электрическую энергию легко дробить на любые части в электрических цепях (мощность приемников электроэнергии может быть от долей ватта до тысяч киловатт); процессы получения, передачи и потребления электроэнергии легко поддаются автоматизации; процессы, в которых используется электрическая энергия, допускают простое управление (нажатие кнопки, выключателя и т. д.). Особо следует отметить существенное удобство применения электрической энергии при автоматизации производственных процессов, благодаря точности и чувствительности электрических методов контроля и управления. Использование электрической энергии позволило повысить производительность труда во всех областях деятельности человека, автоматизировать почти все технологические процессы в промышленности, на транспорте, в сельском хозяйстве и быту, а также создавать комфорт в производственных и жилых помещениях. Кроме того, электрическую энергию широко используют в технологических установках для нагрева изделий, плавления металлов, сварки, электролиза, получения плазмы, получения новых материалов с помощью электрохимии, очистки материалов и газов и т. д. В настоящее время электрическая энергия является практически единственным видом энергии для искусственного освещения. Можно сказать, что без электрической энергии невозможна нормальная жизнь современного общества. Основным законом электротехники, при помощи которого можно изучать и рассчитывать электрические цепи постоянного тока, является закон Ома для участка цепи: отношение напряжения между концами проводника, являющегося однородным участком цепи, к силе тока в этой цепи есть величина постоянная: 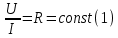 Закон Ома для полной цепи: сила тока, текущего по цепи, пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи: 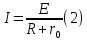 Сложная цепь – цепь, в которой имеется больше одного источника питания или больше одного потребителя электрической энергии и источники напряжения могут соединяться различными способами: параллельными и смешанными. Для расчёта таких цепей применяются первый и второй законы Кирхгофа. Первый закон Кирхгофа: сумма токов направленных к узлу, равна сумме токов направленных от узла. Или другими словами: алгебраическая сумма токов в узле равны нулю: 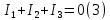 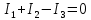 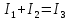 Второй закон Кирхгофа: Алгебраическая сумма всех действующих ЭДС в любом контуре электрической цепи равна алгебраической сумме всех падений напряжений на резисторах входящих в данный контур: 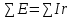 Число уравнений можно уменьшить и упростить расчёт, если ввести понятие контурных токов и применить их для расчёта задачи. Контурный ток – некоторая расчётная величина, которая одинакова для всех ветвей данного контура. Метод эквивалентного генератора используется для исследования работы какого-либо участка в сложной электрической цепи. Для расчёта однофазных цепей используются формулы: 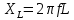 , где , гдеXL – Индуктивное сопротивление L – индуктивность f – частота 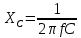 , где , гдеXС - реактивное сопротивление С – ёмкость f – частота Индуктивное сопротивление учитывает противодействие ЭДС самоиндукции периодическим изменением тока. Она пропорциональна частоте этого тока. При постоянном токе XL=0 и катушка индуктивности для постоянного тока представляет собой обычное сопротивление. Реактивное сопротивление не вызывает расхода энергии и показывает, что энергия, запасающая в магнитной катушке не расходуется, а возвращается обратно в цепь. Трёхфазная система применяется во всём мире для передачи и распределения энергии, что позволяет создать надёжные в работе и простые по устройству электродвигатели, генераторы и трансформаторы. Трехфазная система ЭДС – это система трёх переменных ЭДС одинаковой частоты и сдвинутых друг относительно друга по фазе на 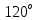 так, что сумма трёхфазных углов равна так, что сумма трёхфазных углов равна 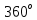 . .У трёхфазных генераторов обмотки часто имеют одну общую точку, в которой соединяются концы обмоток: x, y, z. Такая система называется звездой, а общая точка – нулевой точкой. С приёмником энергии генератор соединятся 3-4 проводами. Три из них называются линейными, а 4-й нейтральным. Напряжение между линейными проводами и нейтральным проводом называется фазным напряжением. В схеме соединения обмоток трёхфазного генератора, которую называют треугольником, конец первой обмотки соединяется с началом второй, конец второй обмотки – с началом третьей и конец третьей с началом первой. При соединении треугольником трёх обмоток источника из трёх фаз приёмника образуется замкнутый контур. Общие точки двух фаз источника и приёмника соединяются между собой линейными проводами. 1 Расчетная часть 1.1 Расчет простых электрических цепей постоянного тока 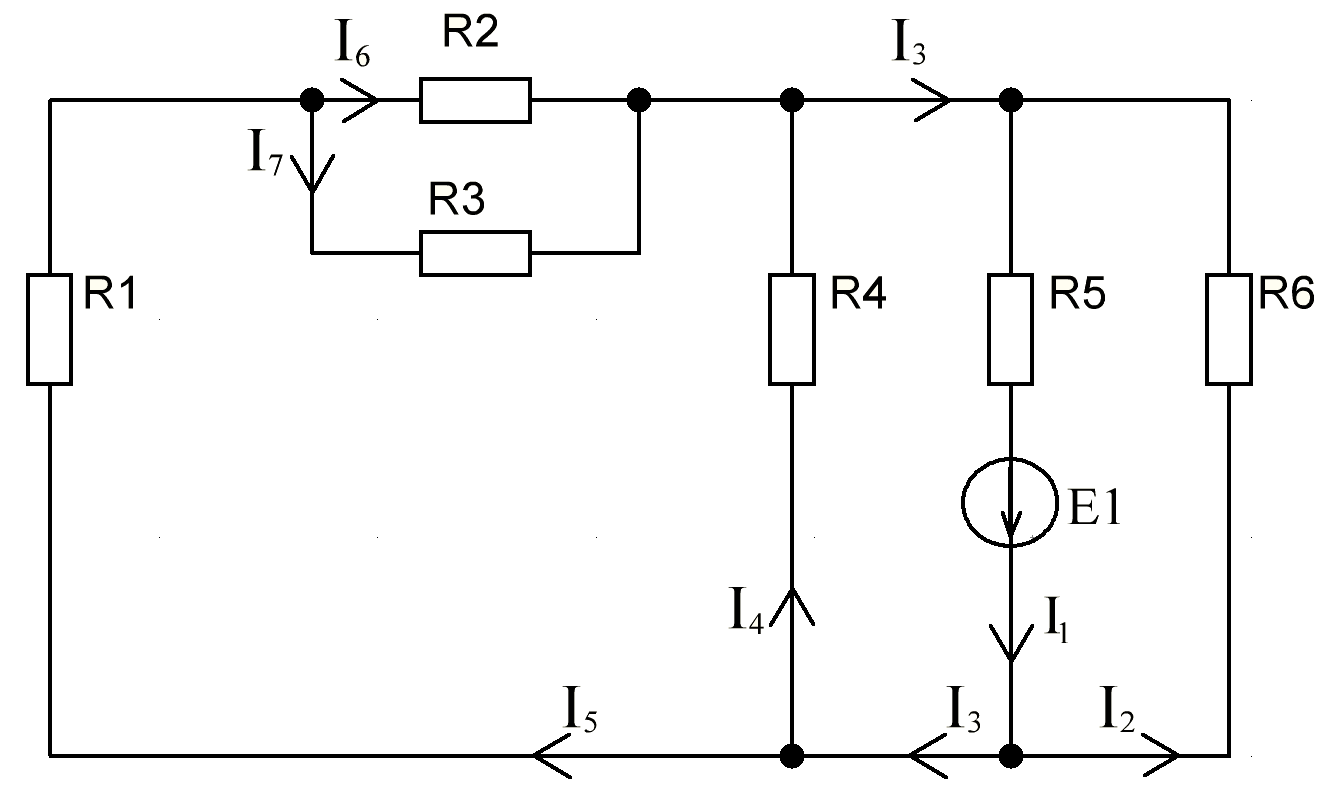 Рис 1.1 Дано: Е = 40 В, R1 = 42 Ом, R2 = 24 Ом, R3 = 56 Ом, R4 = 32 Ом, R5 = 18 Ом, R6 =12 Ом, r = 2 Ом. Определить: I1, I2, I3, I4, I5, I6, I7. Решение. 1.1.1 Расчёт токов в ветвях электрической цепи. Определение эквивалентного сопротивления цепи. Указываем направления токов в ветвях в соответствии с направлением ЭДС (рис.1.1). Резисторы R1, R4 соединены параллельно. Определяем их эквивалентное сопротивление методом «свертывания». 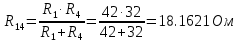 После преобразования схема имеет вид (рис 1.2). 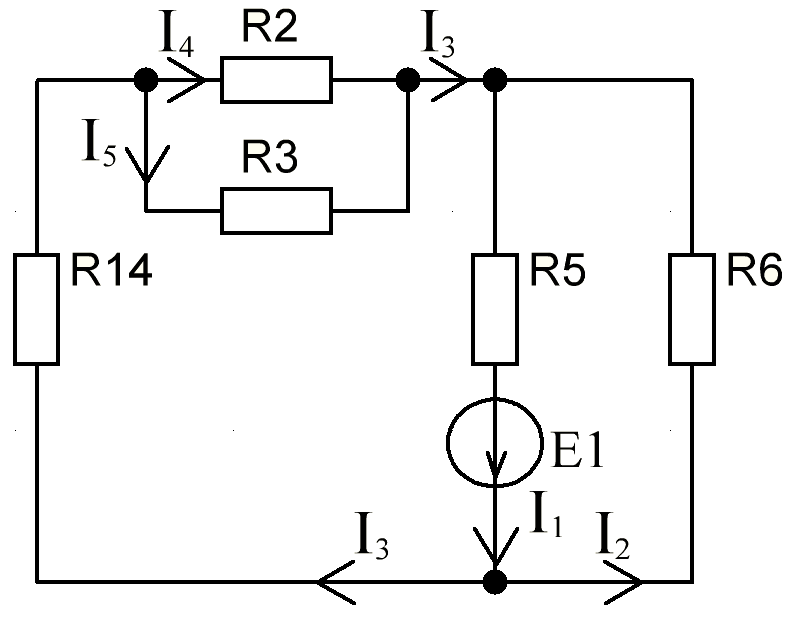 Рис. 1.2 Резисторы R2 и R3 соединены последовательно. Определяем их эквивалентное сопротивление: 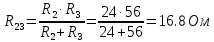 После преобразования схема имеет вид (рис. 1.3). 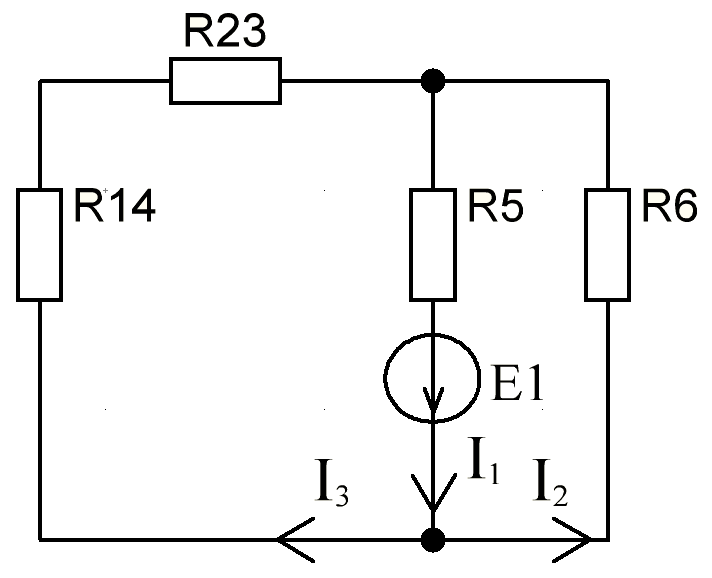 Рис 1.3 Резисторы R14 и R23 соединены последовательно. Определяем их эквивалентное сопротивление: 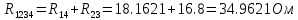 После преобразования схема имеет вид (рис. 1.4). 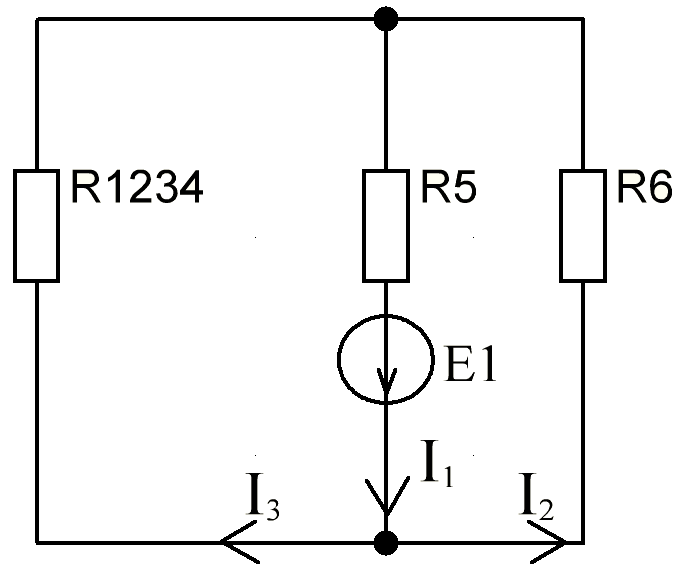 Рис 1.4 Резисторы R1234 и R6 соединены последовательно. Определяем их эквивалентное сопротивление: 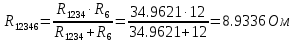 После преобразования схема имеет вид (рис. 1.5). 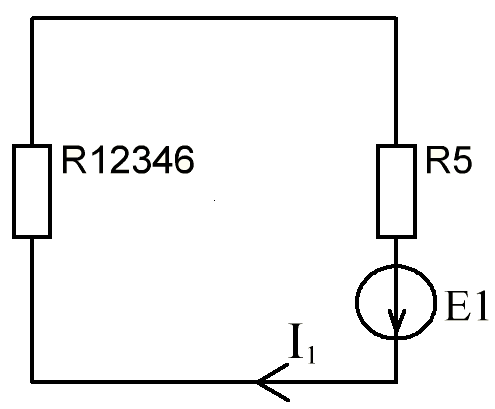 Рис 1.5 Резисторы R12346 и R5 соединены последовательно. Определяем эквивалентное сопротивление цепи: 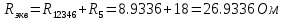 Определяем токи в ветвях электрической цепи. По закону Ома для полной цепи находим общий ток: 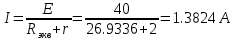 Для определения токов I2 и I3 находим напряжение U12346: 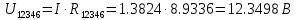 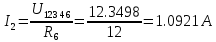 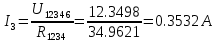 Для определения токов I4, I5 находим напряжение U14: 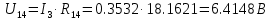 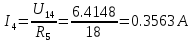 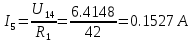 Для определения токов I6 и I7 находим напряжение U23: 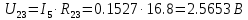 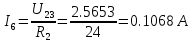 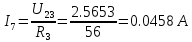 Составляем уравнение баланса мощностей: 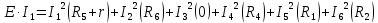 + +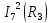 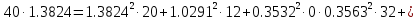 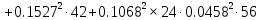 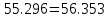 Баланс сходится, но имеется погрешность. 1.2 Расчет сложных электрических цепей постоянного тока Дано: Е1= 30 В, Е2 = 20 В, E3= 0 В, R1 = 45 Ом, R2 = 53 Ом, R3 = 32 Ом, R4 = 24 Ом, R5 = 61 Ом, r01 = 1 Ом, r02 = 1 Ом. Определить: I1, I2, I3. 1.2.1 Расчет электрической цепи методом узловых и контурных уравнений. 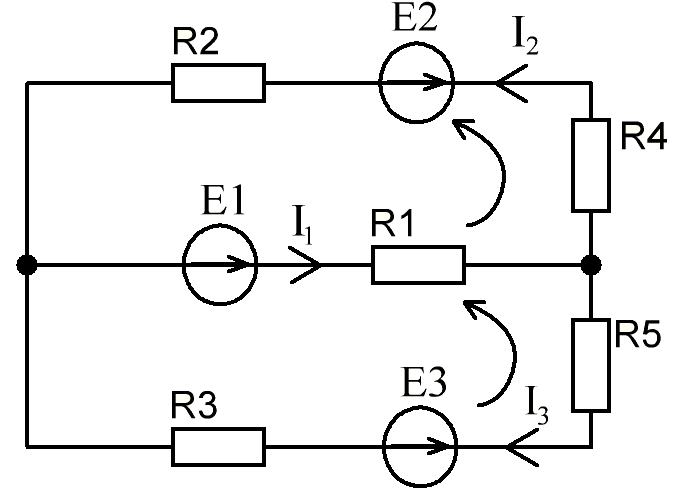 Рис. 2.1 Произвольно указываем направления токов в ветвях электрической цепи (рис. 2.1), составляем систему уравнений по законам Кирхгофа для определения токов в ветвях. Система уравнений для расчета токов: 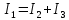  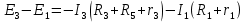 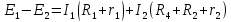 Подставляем значения сопротивлений и ЭДС. Выражаем ток I3, выражаем ток I2: 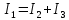  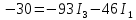 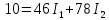  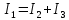 (7) (7)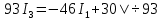 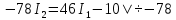 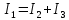 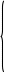 (10) (10)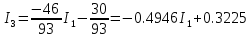 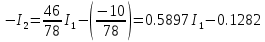 Подставляем значения I3 и I2 в уравнения: 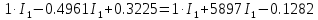 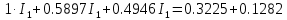 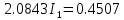 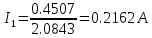 Подставляем значение I1 в уравнения: 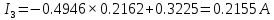 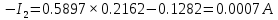 Составляем уравнение баланса мощностей: 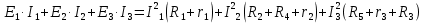 Подставляем значения в формулу: 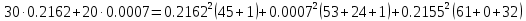 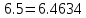 Баланс сходится. Имеется незначительная погрешность. 1.2.2 Расчет электрической цепи методом двух узлов Данный метод применяется в схемах содержащих два узла. 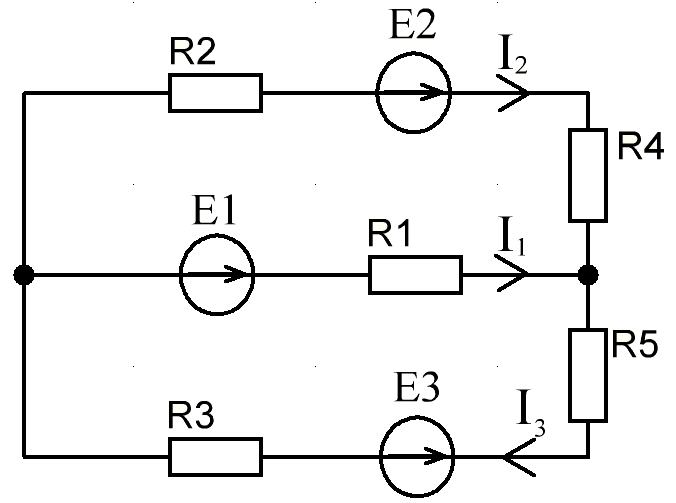 Рис. 3.1 Произвольно указываем направления токов в ветвях электрической цепи (рис. 3.1). Находим напряжение для каждого узла: 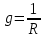 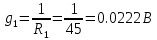 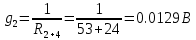 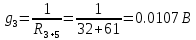 Находим узловое напряжение: 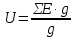 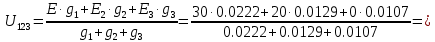 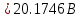 Находим токи для каждой ветви: 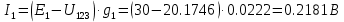 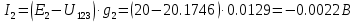 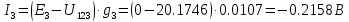 Делаем проверку: 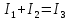 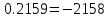 Составляем уравнение баланса мощностей: 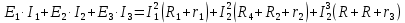 Подставляем значения в формулу: 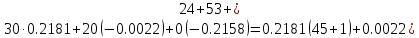 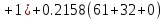 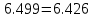 Баланс сходится. Имеется небольшая погрешность. 1.2.3 Расчет электрической цепи методом наложения токов. При решении этим методом из схемы поочередно убираем по одному источнику, дабы сложная схема стала простой. Токи в таких схемах называются частичными, обозначаются 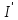 . .Исключаем из схемы (рис. 4.1) источник E2, E3: 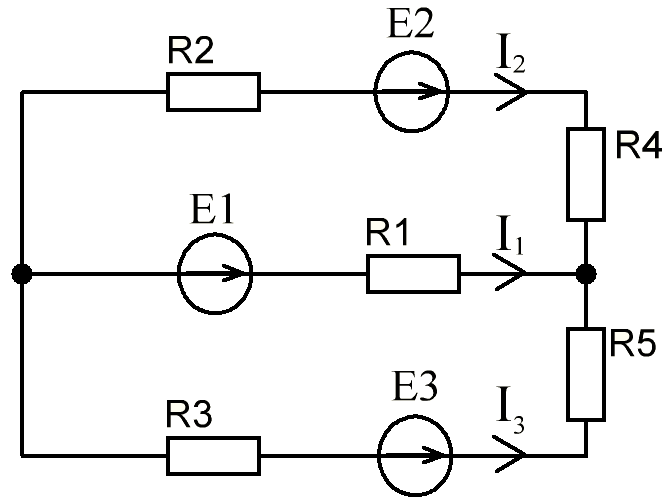 Рис 4.1 Схема с исключёнными источниками имеет вид (рис. 4.2): 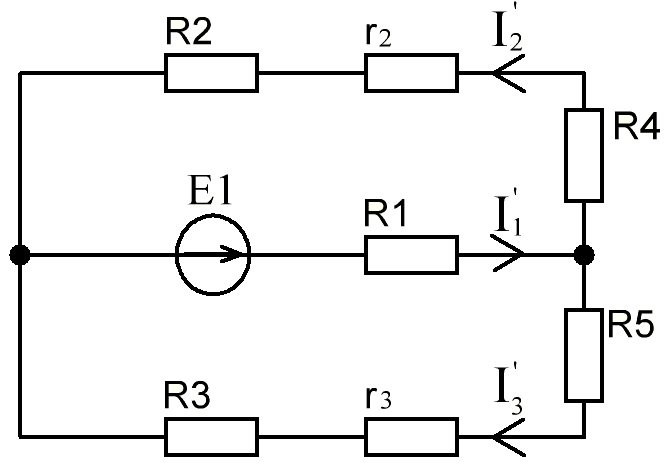 Рис. 4.2 Вычисляем эквивалентное сопротивление цепи: 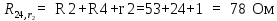 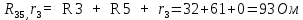 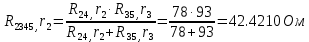 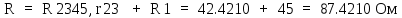 Определяем ток 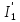 : :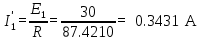 Для определения токов 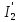 и и 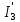 находим падение напряжения находим падение напряжения 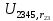 : :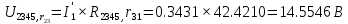 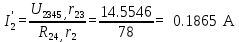 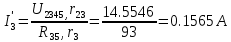 Исключаем из схемы источники E1, E3 (рис. 2.5): 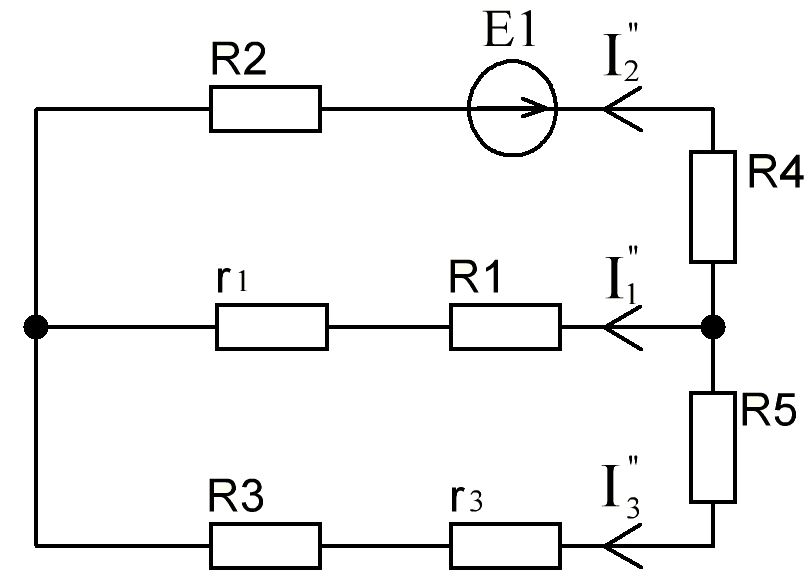 Рис. 4.3 Вычисляем эквивалентное сопротивление цепи: 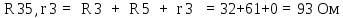 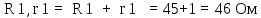 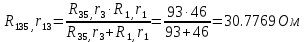 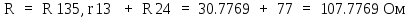 Определяю ток 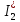 : : 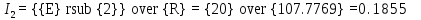 Для определения токов 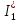 и и 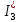 находим падение напряжения находим падение напряжения 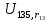 : :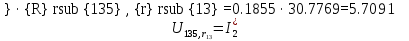 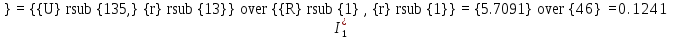 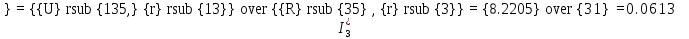 Вычисляем действительные токи в ветвях наложением частичных токов с учетом их направления: 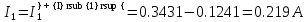 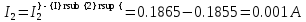 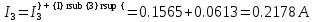 Составляем уравнение баланса мощностей: 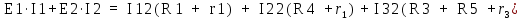 Подставляем значения: 30 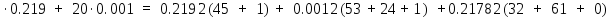 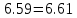 Баланс сходится, но с небольшой погрешностью. 1.2.5 Расчет потенциалов точек. Заземлю одну из точек контура, пусть это будет точка 1 (рис. 5.1): 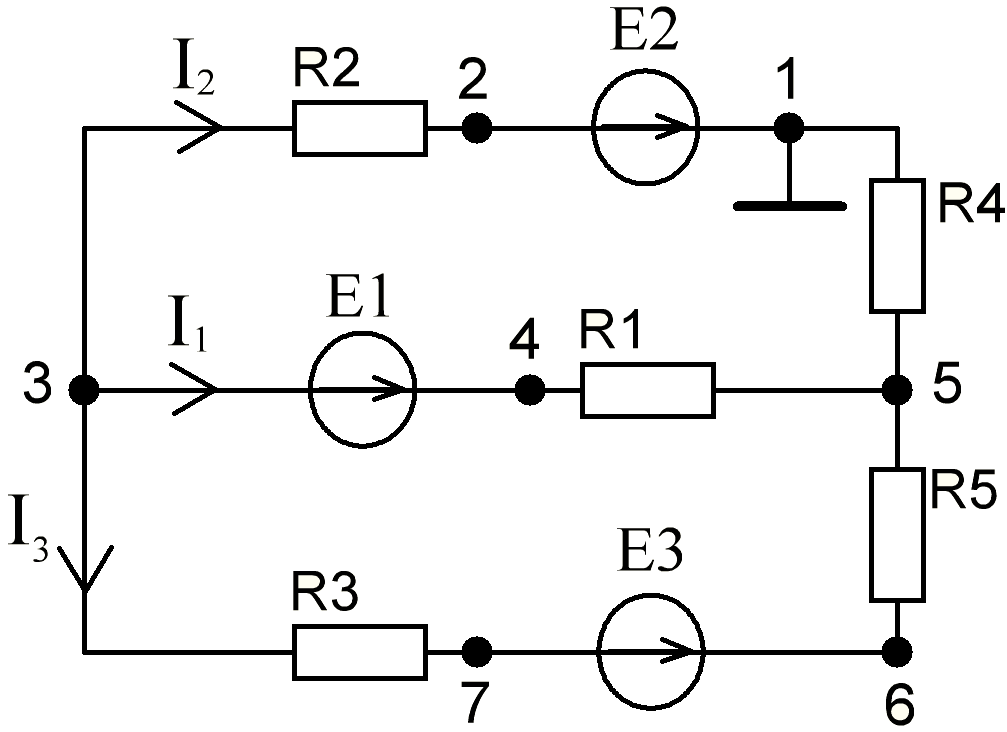 Рис. 5.1 Берем токи из метода расчета двух узлов: 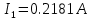 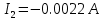 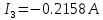 Потенциал точки 1 равен нулю: φ1=0 В. Зная величину, ток ветвей и ЭДС, а также величины сопротивлений, вычислю потенциалы всех точек контура при переходе от элемента к элементу: 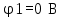 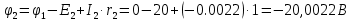 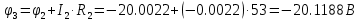 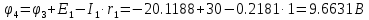 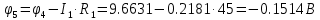 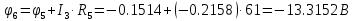 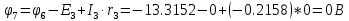 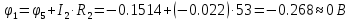 – проверочная точка. – проверочная точка. 1.3 Расчет однофазных электрических цепей переменного тока. 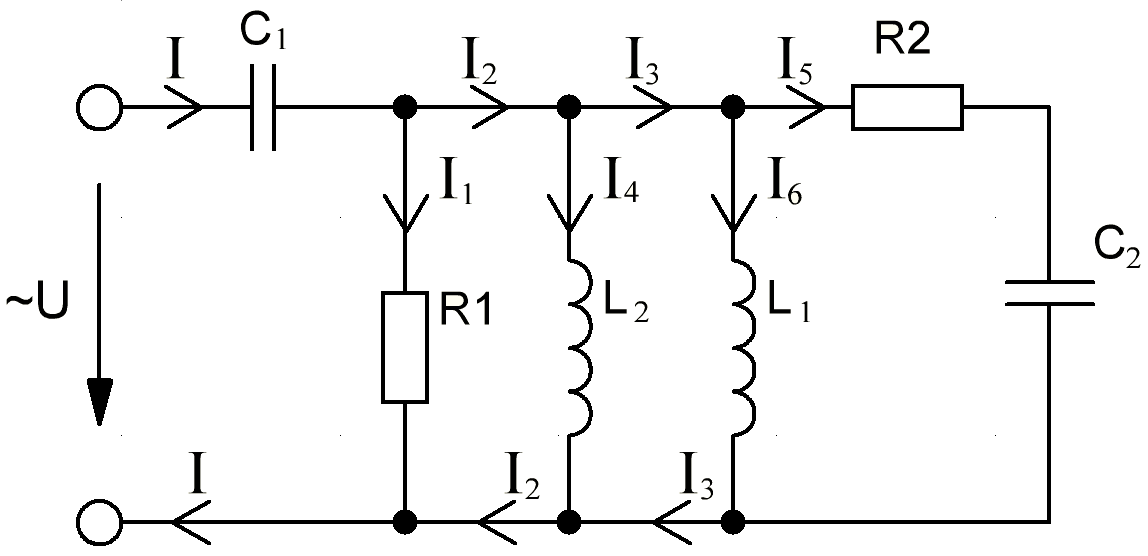   Рис. 6.1 Дано: Um= 180 B, ᵠ= 0о, R1= 20 Ом, R2= 30 Ом, L1= 127.2 мГн, L2= 63.8 мГн, C1= 159 мкФ, C2= 159 мкФ. Определить: I, I1, I2, I3, I4, I5, I6, P, Q, S Построить векторную диаграмму Решение. Схема замещения (6.2): 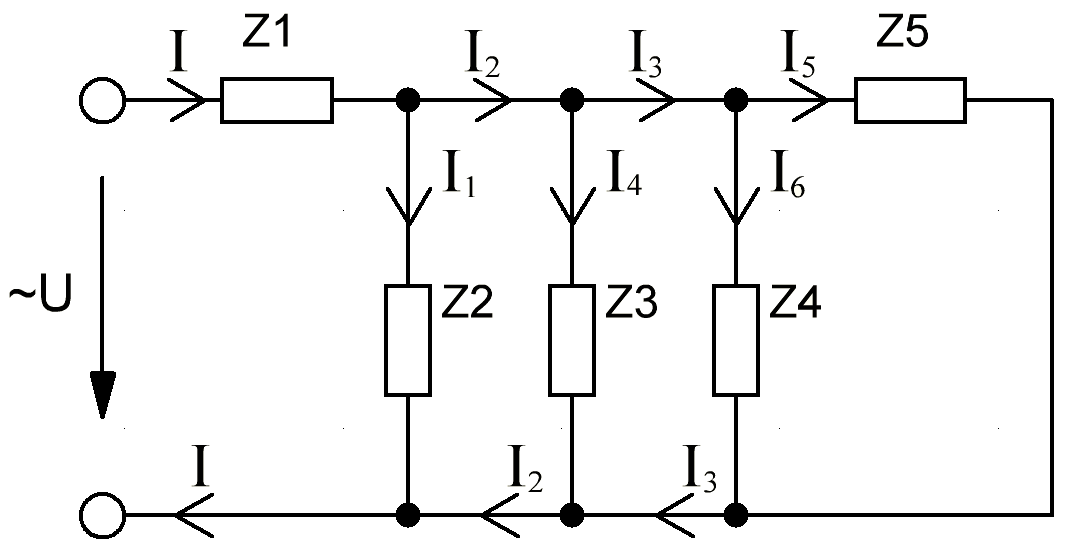 Рис. 6.2 Найду комплексные сопротивления ветвей и реактивное сопротивление элементов, затем участков цепи и всей цепи: 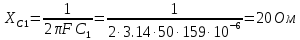 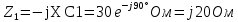 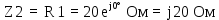 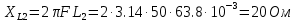 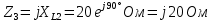 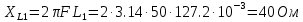 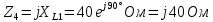 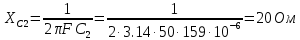 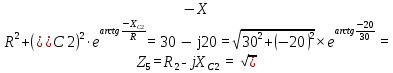 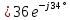 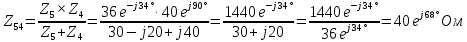 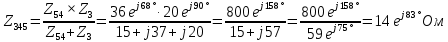 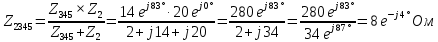 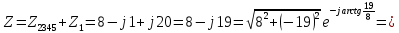 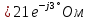 Выражаем значение напряжений в комплексной форме: 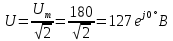 Находим общий ток в цепи, вычисляем напряжение на участках цепи и найдем токи ветвей: 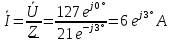 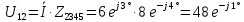 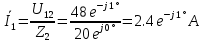 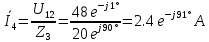 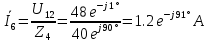 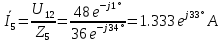 Рассчитываю комплексную мощность цепи: 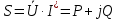 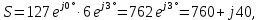 где: 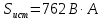 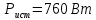 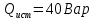 Активная Pпр и реактивная Qпр мощность приемников: 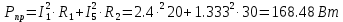 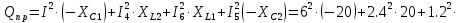 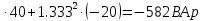 Баланс мощностей не выполняется, мощность рассчитана не верно: 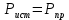 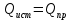 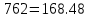 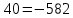 По найденным значениям построим векторы токов. Масштаб тока выберем: 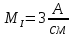 Рассчитаю длины векторов с учетом масштаба: 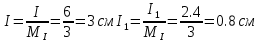 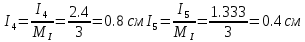  Векторная диаграмма изображена на рисунке 6.3 1.4 Расчет трехфазных линейных электрических цепей переменного тока при построении звездой. 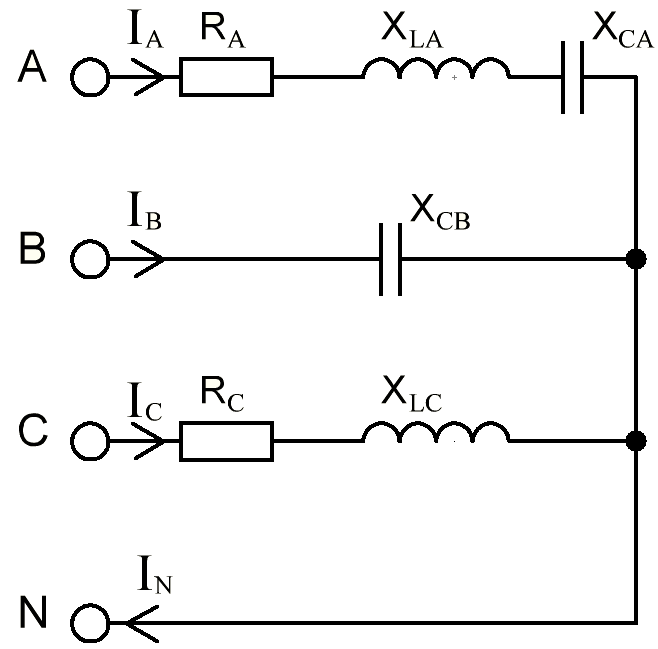 Рис. 7.1 Дано: Uл = 400 В, RА = 35.35 Ом, RC = 10.58 Ом, XLA = 35.35 Ом, XLC =22,65 Ом, XCA=12.96 Ом, XCB = 32.8 Ом. Определить: ZA, ZB., ZC, IA, IB, IC, P, Q, S Символический метод расчета Схема замещения (рис 7.2): 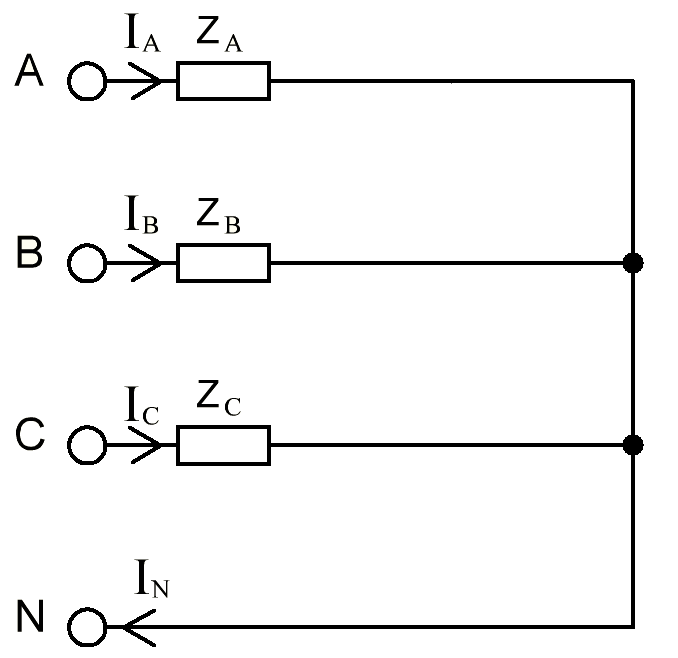 Рис. 7.2 При соединении звездой 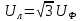 , поэтому , поэтому 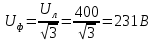 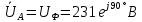 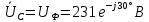 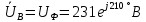 Переводим в показательную форму: 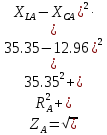 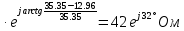 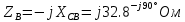 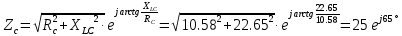 Находим токи в показательной форме: 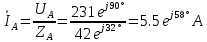 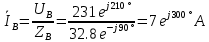 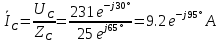 Находим алгебраическую форму записи токов: 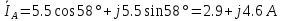 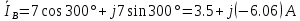 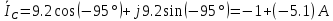 Вычисляем ток в нейтральном проводе: 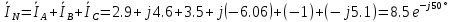 Вычисляем мощность фазы всей цепи: 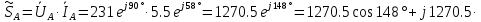 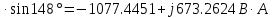 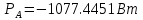 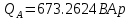 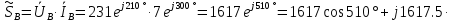 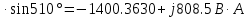 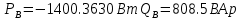 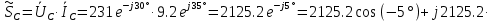 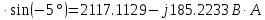 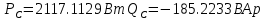 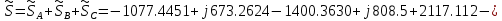 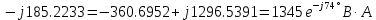 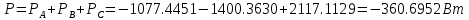 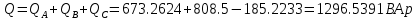 Выполняем проверку мощностей: 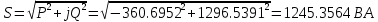 Построю векторную диаграмму фазных напряжений отложенных относительно друг друга под углом 120 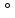 с учетом масштаба: с учетом масштаба: MU=21 B/cм, Mi=2 А/см. Длины векторов: 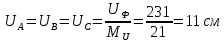 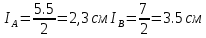 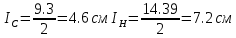 Векторная диаграмма изображена на рисунке 7.3 1.5 Расчет трехфазных линейных электрических цепей переменного тока при построении треугольником. 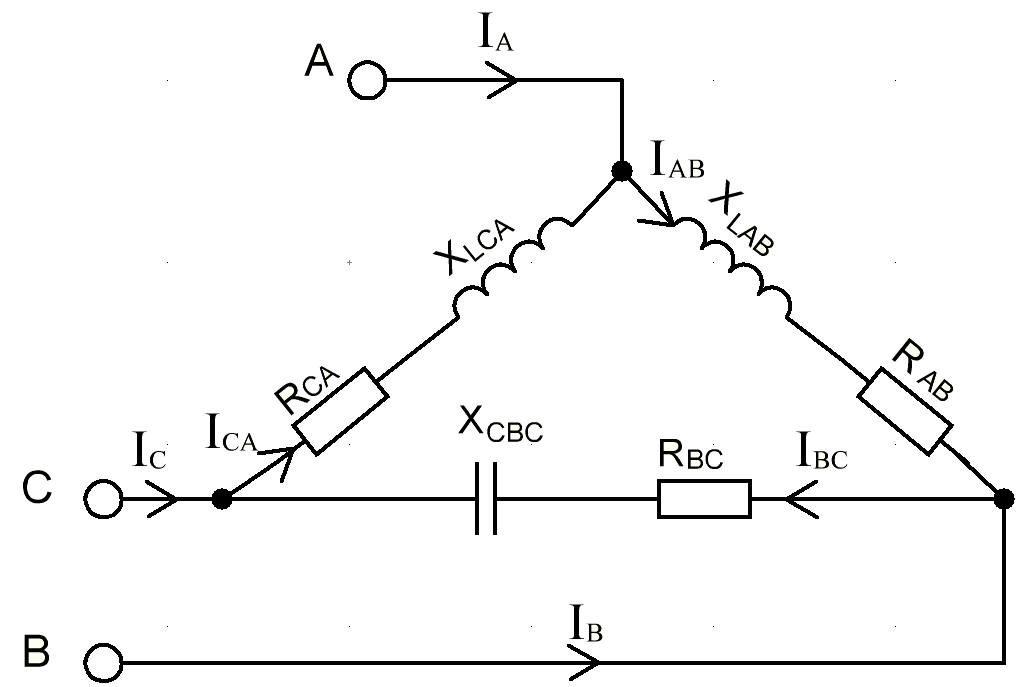   Рис. 8.1 Графоаналитический метод расчета Дано: UЛ = 400 B; RAB = 35.35 Ом; RBC = 22.96 Ом; RCA = 10.58 Ом; XLAB= 35.35 Ом; XLCA= 22.65 Ом; XCBC = 32.8 Ом. Модули фазных напряжений при соединении треугольником равны линейным напряжениям 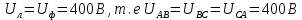 Рассчитаем сопротивление фаз: 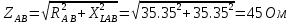 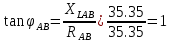 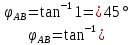 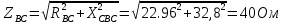 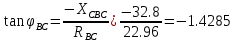 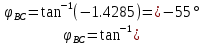 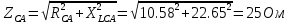 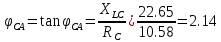 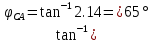 Рассчитываем фазные токи: 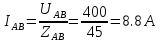 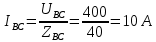 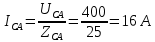 Рассчитываем мощность фаз: 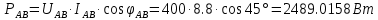 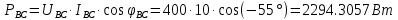 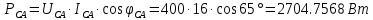 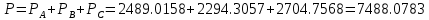 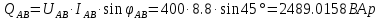 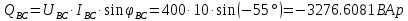 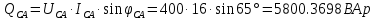 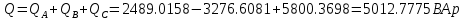 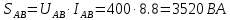 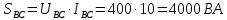 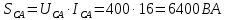 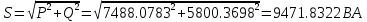 Построим векторную диаграмму, начнем с фазных напряжений отложенных относительно друг друга под углом 120 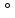 с учетом масштаба: с учетом масштаба: MU=44 B/cм, MI = 4 А/см. Длины векторов: 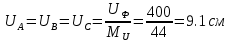 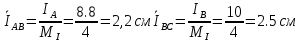 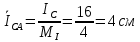 Векторная диаграмма изображена на рисунке 8.2 2. Заключение Для расчёта линейных электрических цепей постоянного тока применяются следующие законы: закон Ома для замкнутой цепи (сила тока, текущего по цепи пропорциональна полному сопротивлению цепи) первый закон Кирхгофа (в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений). Метод расчета в электрической цепи зависит от типа соединения элементов самой цепи. Расчёт нелинейных цепей осуществляется графическим методом. Исходные данные для расчёта задаются в виде графиков или таблиц. Задачи решают следующим образом: заданную величину отмечают на оси координат, находят соответствующую точку кривой, а затем на другой оси определяют искомую величину. При расчёте цепей переменного тока чаще всего используются понятия действующего значения тока, напряжения, ЭДС: 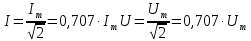 Это условие справедливо только для синусоидального тока. Выбор схемы подключения трёхфазного приёмника производится путём сравнения номинального напряжения сети. Литература Евдокимов Ф.Е. “Теоретические основы электротехники” Мансуров И.И., Попов В.С. “Теоретическая электротехника” Частоедов Л.А. “Электротехника” Шебес М.О. “Сборник задач по теории электрических цепей” ВГПК.390232.К.20.015 ВР |
