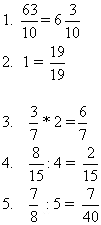Чтение и запись десятичных дробей. урок5 кл. Ема Понятие десятичной дроби. Чтение и запись десятичных дробей. Цели
 Скачать 47.74 Kb. Скачать 47.74 Kb.
|
|
ема: Понятие десятичной дроби. Чтение и запись десятичных дробей. Цели: Формирование знаний и умений записывать и читать десятичные дроби. Познакомить учащихся с новыми числами – десятичными дробями (новым способом записи числа) Развивать интуицию, догадку, эрудицию и владение методами математики. Пробудить математическую любознательность и инициативу, развивать устойчивый интерес к математике. Воспитывать культуру математического мышления. Развивающая цель: Формирование навыков самооценки и самоанализа учебной деятельности. Проблемно – развивающий урок (комбинированный) Этапы: 1) проблемная ситуация; 2) проблема; 3) поиск приёмов её решения; 4) решение проблемы Девиз урока: «Знания имей отличные по теме «Дроби десятичные» Задача урока: доказать, что дроби не смогут поставить нас в трудное положение. Эпиграфы: «Математику нельзя изучать, наблюдая, как это делает сосед» (поэт Нивей) «Учиться надо весело… Чтобы переваривать знания, надо поглощать их с аппетитом» (Анатоль Франс) Оборудование: индивидуальные карты – задания; карты- задания для работы в парах; наглядность для устной работы, для исторической справки; магнитная доска Повторение: Обыкновенные дроби Геометрические фигуры Ход урока Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому будем сегодня работать все активно, хорошо и с пользой для ума. I. «Звёздный час обыкновенной дроби» - устная работа Первый тур
Какая из дробей выражает «четверть»? Назовите дробь, равную дроби Назовите дробь, равную 4. Какая дробь выражает «половину»? Назовите дробь больше 1, но меньше 2. Назовите неправильные дроби. Второй тур «Логические цепочки»
Расположи в порядке возрастания. Третий тур. Ученик допустил ошибку при применении основного свойства дроби. Найди ошибку! Четвёртый тур
Изучение новой темы Рассмотрим таблицу разрядов и ответим на вопросы:
Вопросы: Как меняется положение единицы в каждой следующей строке по сравнению с предыдущей? Как при этом меняется её значимость? Как меняется величина соответствующего числа? Какое арифметическое действие соответствует этому изменению? Вывод:перемещая единицу на один разряд вправо, мы каждый раз уменьшали соответствующее число в 10 раз и делали это, пока не дошли до последнего разряда – разряда единиц. А можно ли и единицу уменьшить в 10 раз? Конечно, Проблема: Но вот места для этого числа в нашей таблице разрядов пока нет. Подумайте, как надо изменить таблицу разрядов, чтобы в ней можно записать число Рассуждаем, надо цифру 1 сдвинуть вправо на один разряд. Аналогично: Дать названия разрядам: десятые, сотые, тысячные, десятитысячные и т.д. целая часть дробная часть
Работа по таблице. Прочитать числа, записанные в таблице. 2 единицы 3 десятых 2 единицы 3 сотых А чтобы записать числа вне таблицы нам необходимо отделять каким – либо знаком целую часть от дробной. Договорились делать это с помощью запятой или точки. В нашей стране, как правило, используется запятая, а в США и некоторых других странах – точка. Числа записываем и читаем следующим образом: а) 2,3 или 2.3 (две целых три десятых или два, запятая, три или два, точка, три) б) 2,03 или 2.03 (две целых три сотых или два, запятая, ноль, три или два, точка, ноль, три) Правило: Если в десятичной записи числа использованы запятая (или точка), то говорят, что число записано в виде десятичной дроби. Для краткости числа называют просто десятичными дробями. Заметим, что десятичная дробь – это не новый тип числа, а новый способ записи числа. Итак, девиз нашего урока: «Знания имей отличные по теме «Дроби десятичные» Задача урока: доказать, что дроби не смогут поставить нас в трудное положение. А сейчас посетим «Деревню Историческую» Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби. Действия над дробями в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби». Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввёл в 1585году голландский математик и инженер Симон Стевин. Вот как он изображал дробь: 14,382, 14 0 3 1 8 2 2 3 Во Франции десятичные дроби ввёл Франсуа Виет в 1579 году; его запись дроби: 14,382, 14/382, 14 А у нас учение о десятичных дробях изложил Леонтий Филиппович Магницкий в 1703 году в учебнике математики «Арифметика, сиречь наука числительная» Вот ещё некоторые способы изображения десятичных дробей: 14. 3. 8. 2. ; Зарядка (музыкальное сопровождение) II. Упражнения Запись темы урока. Первая таблица – записать самостоятельно числа. Вторая таблица – записать числа по разрядам. III. Переменка – проводится для того, чтобы сохранить хорошее настроение, бодрость духа, математический настрой. Анатоль Франс когда – то сказал: «Учиться надо весело…Чтобы переваривать знания, надо поглощать их с аппетитом» Устно: Витя Верхоглядкин отыскал правильную дробь, которая больше 1, но держит своё «открытие в секрете». Почему? Витя Верхоглядкин провёл 11 диаметров окружности. Потом он подсчитал число проведённых радиусов и получил число 21. Правильный ли его ответ? Шёл отряд солдат: десять рядов по семь солдат в ряд. Сколько? а) Сколько там было усатых солдат? Сколько там было безусых солдат? б) Сколько там было носатых солдат? Сколько там было курносых солдат? Запись: IV. Повторение – развивающие упражнения (работа в парах) Озеро Ребусное ( Приложение) V. Итог урока. Рефлексия. - Что нового для себя узнали? - В чём затруднялись? - Чему научились? - Какую проблему ставили на уроке? - Удалось ли нам её решить? Оценка своей работы (на листочках, где таблицы разрядов). Напишите, как усвоили материал урока. Получил хорошие знания. Усвоил весь материал. Усвоил материал частично. VI. Домашнее задание. № 38.1, 38.2 , Рабочая тетрадь (стр. 28) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||