|
|
Энергия волн для Соловьева В.Г.. Энергия волн
ЭНЕРГИЯ ВОЛН
12.1. Введение
Огромные количества энергии можно получить от морских волн. Мощность, переносимая волнами на глубокой воде, пропорциональна квадрату их амплитуды и периоду. Поэтому наибольший интерес представляют длиннопериодные (Т=10 с) волны большой амплитуды (а =2 м), позволяющие снимать с единицы длины гребня в среднем от 50 до 70 кВт/м.
Возможность преобразования энергии волн в электроэнергию доказана уже давно. Существует множество технических решений, позволяющих реализовать эту возможность. В последние годы интерес к волновой энергетике резко усилился, особенно в Японии, Великобритании, странах Скандинавии, в результате чего эксперименты переросли в стадию реализации проектов. Современная тенденция разработки таких установок, как и вообще установок на возобновляемых видах энергии, ориентируется на единичные модули умеренной мощности (около 1 МВт) размером порядка 50 м вдоль фронта волны. Подобные устройства уже сейчас могут принести определенные экономические выгоды в случае замены дизельных генераторов, снабжающих энергией удаленные поселки, особенно на островах.
Развитие волновой энергетики сопряжено со значительными трудностями. Их подробный анализ дан ниже, но в основном они сводятся к следующему.
1. Волны нерегулярны по амплитуде, фазе и направлению движения. Проектировать же устройства для эффективного извлечения энергии в широком диапазоне варьирующихся величин не просто.
2. Всегда есть вероятность возникновения экстремальных штормов и ураганов, во время которых образуются волны очень большой интенсивности. Конструкции волноэнергетическнх устройств должны, разумеется, им противостоять. Примерно раз в 50 лет возникают волны, амплитуда которых в 10 раз превышает среднюю. Следовательно, во время штормов конструкции должны выдерживать нагрузки, примерно в 100 раз большие, чем при нормальной работе.
3. Подобные пиковые величины мощности присущи главным образом именно волнам на глубокой воде, проходящим со стороны открытого моря. Трудности, связанные с созданием энергетических устройств для таких волновых режимов, их обслуживанием, удержанием в заданном положении, передачей энергии на берег, вызывают опасения.
4. Обычно период волн Т=5-10 с (частота порядка 0,1 Гц). Достаточно трудно приспособить это нерегулярное медленное движение к генерированию электроэнергии промышленной частоты, которая в 500 раз выше.
5. Выбрать подходящий тип устройства для преобразования энергии из всего их многообразия - сложная, часто просто непосильная задача.
6. Привычка мыслить категориями крупномасштабной энергетики промышленно развитых районов ведет к искушению создавать лишь крупные волновые электростанции в местах с высокими волновыми потенциалами. При этом существует тенденция игнорировать зоны умеренных потенциалов, где зачастую использование волновой энергии оказывается экономически более оправданным.
Преимущества волновой энергии состоят в том, что она достаточно сильно сконцентрирована, доступна для преобразования и на любой момент времени может прогнозироваться в зависимости от погодных условий. Создаваясь под действием ветра, волны хорошо сохраняют свой энергетический потенциал, распространяясь на значительные расстояния. Например, крупные волны, достигающие побережья Европы, зарождаются во время штормов в центре Атлантики и даже в Карибском море.
12.2. Волновое движение
Наибольшее число волновых энергетических устройств разрабатывается для извлечения энергии из волн на глубокой воде. Это наиболее общий тип волн, существующий при условии, что средняя глубина моря Dпревышает величину половины длины волны λ/2. Например, при характерной длине волны λ 100 м и амплитуде а м волна ведет себя как на глубокой воде при глубине моря, превышающей 30 м. На рис. 12.1, а показано, как движутся частицы жидкости в волне на глубокой воде. Амплитуда кругового движения с глубиной уменьшается экспоненциально и становится пренебрежимо малой при D>λ/2. В волне на мелководье (рис. 12.1, б) частицы движутся по эллиптическим орбитам, движение охватывает придонный слой, приводя к диссипации энергии волны.
 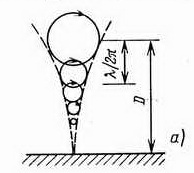 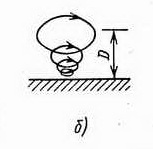
Поверхностные волны на глубокой воде имеют характерные особенности.
1) Волны являются неразрушающимися синусоидальными с нерегулярной длиной, фазой и направлением прихода.
2) Движение каждой частицы жидкости в волне является круговым. В то время как изменяющиеся очертания волн свидетельствуют о распространении волнового движения, сами по себе частицы не связаны с этим движением и не перемещаются в его направлении.
3) Поверхностный слой жидкости остается на поверхности.
4) Амплитуда движения частиц жидкости экспоненциально уменьшается с глубиной. На глубине λ/2π от среднего положения уровня поверхности амплитуда кругового движения частиц уменьшается в е раз (е = 2,72 — основание натуральных логарифмов). На глубине λ/2 перемещение частиц жидкости становится пренебрежимо малым, составляя менее 5% поверхностного.
5) Существенно, что амплитуда волны а не зависит от ее длины λ, скорости распространения с, периода Т, а зависит лишь от характера предшествовавшего взаимодействия ветра с морской поверхностью. В то же время редко создаются условия, при которых амплитуда достигает значения λ/10.
6) Разрушение волны в виде белого буруна происходит, когда наклон ее поверхности составит примерно 1:7. Энергетический потенциал волны при этом рассеивается.
Для волн на глубокой воде силы трения, поверхностного натяжения и инерции малы по сравнению с двумя доминирующими силами — гравитационной и вращательной, поэтому водная поверхность всегда принимает такую форму, чтобы касательная к ней в любой точке была перпендикулярна направлению действия результирующей этих двух сил (рис. 12.2).

Очень важно понимать, что в волнах на глубокой воде нет поступательного движения жидкости (имеется в виду общий горизонтальный перенос массы). Движение взвешенных в воде частиц на рис. 12.1 подтверждает это. На этом же рисунке сравнивается движение частиц в волнах на глубокой и мелкой воде.
В подповерхностном слое жидкости ее частицы совершают круговое движение с радиусом орбиты а, равным амплитуде волны (рис. 12.3).
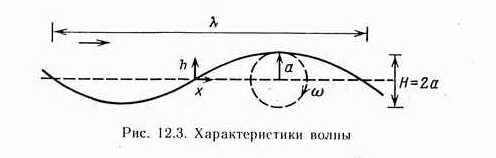
Высота волны Н от вершины гребня до основания равна ее удвоенной амплитуде (Н = 2а). Угловая скорость движения частиц ω измеряется в радианах в секунду. Изменение формы волновой поверхности таково, что наблюдается поступательное движение, хотя сама вода, как уже отмечалось, не перемещается в направлении распространения волны (слева направо). Это кажущееся перемещение есть результат наблюдения фаз смещения последовательно расположенных частиц жидкости; как только одна частица в гребне опускается, другая занимает ее место, обеспечивая сохранение формы гребня и распространение волнового движения вперед.
Результирующая сила F, действующая на поверхностную частицу массой т, показана па рис. 12.4.
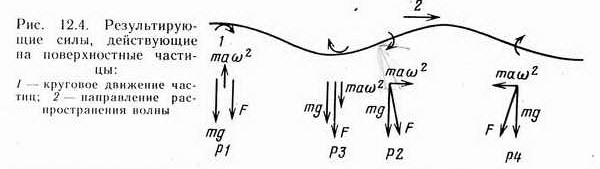
Под действием суммы подобных сил водная поверхность принимает такую форму, при которой касательная в любой точке ее перпендикулярна F. При подъеме на гребень (положение Р1) частица подвергается действию центробежной силы mаω2. В следующий момент частица падает вниз, и ее место занимает соседняя, вращающаяся с задержкой по фазе. В положении Р2 частица оказывается на среднем уровне жидкости, и поверхность ориентируется перпендикулярно результирующей силе F. Во впадине, положение РЗ, направленная вниз сила имеет максимум (центробежная и гравитационная силы складываются). К положению Р4 частица практически полностью завершает цикл движения.
Изменение ускорения поверхностной частицы показано на рис. 12.5, б.
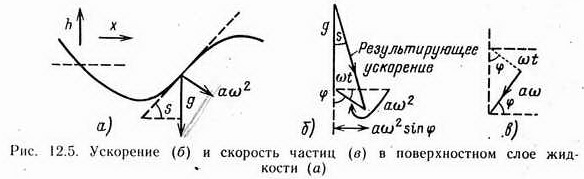
В начальный момент времени частица находится в среднем положении, а затем ее фазовый угол изменяется по закону
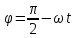 , (12.1) , (12.1)
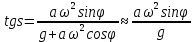 , (12.2) , (12.2)
так как практически для неразрушенной волны g много больше aω2(например, а = 2 м, Т = 8 с, aω2=1,2 м/с2 и g=9,8 м/с2). Пусть h - текущее значение подъема над средним уровнем. Наклон касательной к поверхности волны определяется выражением (см. рис. 12.5, а):
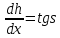 , (12.3) , (12.3)
Из соотношений (12.1) — (12.3) следует, что:
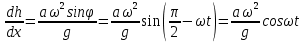 , (12.4) , (12.4)
По диаграмме рис. 12.5, в вертикальная скорость частицы (проекция вектора скорости на вертикальную ось):
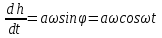 , (12.5) , (12.5)
Решая систему дифференциальных уравнений (12.4) и (12.5), получаем:
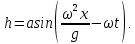 (12.6) (12.6)
Основное уравнение распространения волны длиной λ и скоростью с:
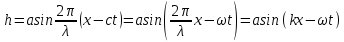 , (12.7) , (12.7)
где k = 2π/λ — волновое число. Сравнивая уравнение волны (жидкости) с основным уравнением распространения волны, видим, что:
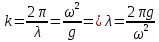 , (12.8) , (12.8)
Это соотношение устанавливает зависимость между частотой, и длиной для поверхностной волны на глубокой воде.
Период движения волны (с учетом (12.8)):
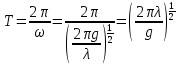 , (12.9) , (12.9)
Скорость частицы жидкости в гребне волны (с учетом (12.8)):
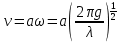 , (12.10) , (12.10)
С учетом (12.8) найдем скорость перемещения поверхности волны в направлении х:
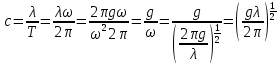 , (12.11) , (12.11)
Скорость c называют фазовой скоростью распространения волн, создаваемых на поверхности жидкости. Следует отметить, что эта величина не зависит от амплитуды волны и неявным образом связана со скоростью движения частиц жидкости в волне.
12.3. Энергия и мощность волны
Основные соотношения. Элементарная теория волн на глубокой воде основана на допущениях о свойствах единичной регулярной волны. Частицы жидкости в такой волне движутся по круговым орбитам с переменной фазой в направлении распространении волны. Амплитуда этого движения в вертикальной плоскости равна половине расстояния от гребня до впадины волны и экспоненциально уменьшается с глубиной. Движение частиц остается круговым при глубине моря D>0,5λ. На таких глубинах перемещения частиц вблизи дна пренебрежимо малы. Для этих условий (рис. 12.6) для частицы, находящейся на расстоянии z от среднего положения уровня поверхности, радиус круговой орбиты r = aekz . (12.13)
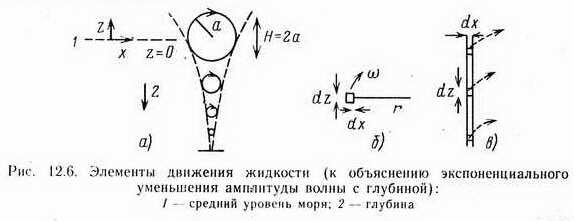
Для положения ниже среднего уровня поверхности z — отрицательная величина.
Выделим элементарный слой единичной ширины в направлении вдоль фронта волны с координатами (x,z). Элемент объема в этом слое (см. рис. 12.6 б, в):
dV=dxdz, (12.14)
а элемент массы при плотности ρ:
dm =ρdV=ρdxdz. (12.15)
Пусть Ek — полная кинетическая энергия волнового движения этого слоя на единицу длины в направлении х. Соответственно полная кинетическая энергия на длине δх есть Ekδх. Каждый элемент этого слоя высотой δz и длиной δx находится в круговом движении с постоянной угловой скоростью ω, радиус круговой орбиты равен r, а линейная скорость v=rω (рис. 12.6, б). Вклад каждого элемента в полную кинетическую энергию составляет δEkδх, причем c учетом (12.15):
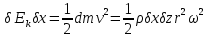 , (12.16) , (12.16)
Следовательно, 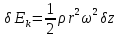 . (12.17) . (12.17)
Наиболее просто предположить, что в начальный момент времени такой элемент находится в каком-то среднем положении по отношению к слою, а все другие элементы этого слоя движутся вертикально в фазе с ним в направлении z (рис. 12.6, в).
Так как радиус круговой орбиты в волне r = aekz (z ниже поверхности отрицательно), то (12.17) преобразуется к виду:
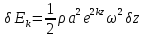 , (12.18) , (12.18)
и полная кинетическая энергия всего этого вертикального слоя на длине δx равна:
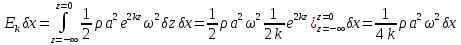 , (12.19) , (12.19)
Так как k = 2π/λ, с учетом (12.8):
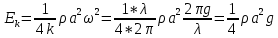 , (12.20) , (12.20)
Таким образом, полная кинетическая энергия на единицу ширины волнового фронта и единицу длины вдоль направления распространения волны равна:
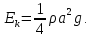 (12.21) (12.21)
Нормированная потенциальная энергия волны равна в точности такой же величине (выводим по аналогии):
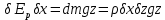 ; ;
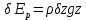 ; ;
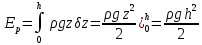 ; ;
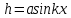 - уравнение движения волновой поверхности, без учета изменения ее формы во времени; - уравнение движения волновой поверхности, без учета изменения ее формы во времени;
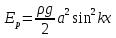 , ,
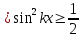 - среднее значение функции; - среднее значение функции;
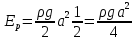 ; ;
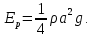 (12.22) (12.22)
Равенство кинетической и потенциальной составляющих энергии — свойство гармонического движения.
Приведенный способ нормирования - нормирование на единицу площади поверхности волны. Полная энергия на единицу площади поверхности волны равна сумме кинетической и потенциальной энергий:
E = Ek + Ep = ρa2g/2. (12.23)
Выражение для энергии на единицу ширины волнового фронта и на единицу длины волны вдоль направления его распространения запишем в виде:
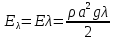 , (12.25) , (12.25)
С учетом (12.8) имеем 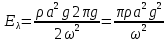 , (12.26) , (12.26)
Или, так как T=2π/ω, 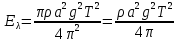 . (12.27) . (12.27)
Отбор мощности от волн. Предположим, что единичный элемент или частица жидкости находится ниже среднего уровня поверхности (рис. 12.7). Для поверхностной волны с амплитудой а и волновым числом k радиус движения части в подповерхностном слое определяется уже известным выражением
r = аекz. (12.28)
Вертикальное перемещение Δу (рис 12.7, б)

из среднего положения описывается выражением:
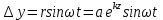 . (12.29) . (12.29)
Горизонтальная составляющая скорости частицы определяется соотношением (см. рис. 12.7, б): 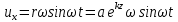 . (12.30) . (12.30)
Из рис. 12.7, а следует, что мощность, переносимая волной в направлении х на единицу ширины волнового фронта, в любой момент равна:
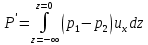 , (12.31) , (12.31)
где р1 и р2 — давления, действующие на элемент высотой dz единичной ширины в направлении вдоль волнового фронта. В свою очередь (р1 - р2) — разность давлений, испытываемая элементом жидкости в горизонтальном направлении. Единственная составляющая энергии, не обращающаяся в нуль при прохождении элементом положения среднего уровня поверхности, связана с изменением потенциальной энергии в результате вращения частиц по круговым орбитам:
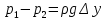 . (12.32) . (12.32)
Подставляя вместо Δу его выражение из (12.29), получаем:
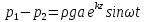 . (12.33) . (12.33)
С использованием (12.30) и (12.33) выражение (12.31) приобретает вид:
 . (12.34) . (12.34)
Осреднение по времени за несколько периодов дает для sin2ωt значение 1/2, так что:
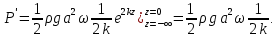 (12.35) (12.35)
Фазовая скорость волны:
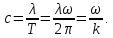 (12.36) (12.36)
С учетом (12.36) выражение для мощности (12.35), переносимой в направлении распространения волны на единицу ширины волнового фронта, приобретает вид:
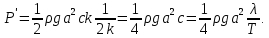 (12.37) (12.37)
С учетом (12.23) и (12.37) мощность равна полной энергии (кинетическая и потенциальная) Е в волне на единицу площади поверхности, умноженной на величину u=с/2 - групповую скорость волн на глубокой воде, с которой волны переносят энергию. С учетом выражения для групповой скорости:
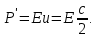 (12.38) (12.38)
Из (12.8): 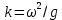 , (12.39) , (12.39)
Следовательно с учетом (12.36): 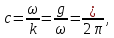 (12.40) (12.40)
Различие между групповой и волновой (фазовой) скоростями является общим для любых волновых процессов, для которых фазовая скорость зависит от длины волны (дисперсия).
Подставляя в (12.37) фазовую скорость в виде (12.40), получаем известное соотношение:
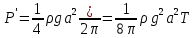 , (12.41) , (12.41)
Следовательно, мощность, переносимая волнами, увеличивается прямо пропорционально квадрату амплитуды и периоду. Именно поэтому для специалистов по океанской энергетике особенно привлекательны длиннопериодные волны океанской зыби, обладающие значительной амплитудой.
12.4. Описание реальных волн
На практике волны оказываются совсем не такими идеализированно синусоидальными, как это подразумевалось выше. Лишь случайно естественные или искусственно созданные в результате дифракции или движения в каналах волны становятся близкими к идеальным. Обычно же в море наблюдаются нерегулярные волны с переменными частотой, направлением и амплитудой. Под воздействием превалирующего ветра движение волн может приобретать преимущественное направление (например, юго-западное или северо-восточное для волн, набегающих на побережье Британских островов), а период стать достаточно большим — наблюдаются волны океанской зыби. Более нестабильные ветры вызывают нерегулярное движение вод с характерным более коротким периодом — штормовые волны. При глубине моря порядка 30 м и менее возможны фокусирующие и направляющие эффекты, в отдельных местах они могут привести к появлению более регулярных или более мощных волн. Волновые энергетические устройства должны противостоять широкому спектру природных условий, должны быть предназначены для извлечения максимума мощности в среднем за достаточно длительный период и независимо от района размещения. При проектировании подобных устройств необходимо в первую очередь понимать возможность значительного усиления воли по сравнению с типичными для данного района по крайней мере раз в 50 лет.
Высота волн в заданной точке наблюдения обычно регистрируется с помощью аналоговых волнографов. Для получения сведений о направлении прихода волн требуются специальные измерения. Представление о записи волнографа даст рис. 12.8.
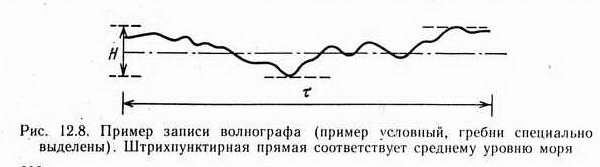
Кривая фиксирует вертикальное перемещение уровня во времени. Современные волнографы используют цифровые методы регистрации с последующей обработкой на ЭВМ больших массивов данных. Если величина Н от измерения к измерению существенно изменяется, то приходится использовать различные методы вычисления статистически обоснованных значений, наилучшим образом отражающих суть явления.
Основными переменными величинами, которые измеряются обычно в течение достаточно длительного времени, являются:

где 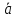 — корень квадратный из среднего квадрата перемещения волной поверхности от положения среднего уровня поверхности, рассчитанный по n измерениям, выполненным за одинаковые интервалы времени, позволяет избежать погрешностей измерения за счет записи волнового процесса на частоте, в 2 раза меньшей, чем максимальная. Измеренная или наиболее вероятная максимальная высота волн Нmax 1 раз в 50 лет может принять значение, равное 50Нs. Именно это значение закладывается в расчеты при проектировании морских сооружений. Средний период колебаний по минимумам Тz определяется как продолжительность промежутка времени между минимумами, пересекающими линию среднего положения уровня поверхности на волнограмме. На рис. 12.8 Тz=τ/3. Средний период колебаний по гребням Тс определяется продолжительностью временного периода τ волнограммы, деленной на число гребней. На рис. 12.8 Тc =τ/10; на практике N очень велико, так что погрешность в определении Тс мала. Параметр уширения спектра ε, характеризующий число составляющих колебаний в волне, можно найти из соотношения: — корень квадратный из среднего квадрата перемещения волной поверхности от положения среднего уровня поверхности, рассчитанный по n измерениям, выполненным за одинаковые интервалы времени, позволяет избежать погрешностей измерения за счет записи волнового процесса на частоте, в 2 раза меньшей, чем максимальная. Измеренная или наиболее вероятная максимальная высота волн Нmax 1 раз в 50 лет может принять значение, равное 50Нs. Именно это значение закладывается в расчеты при проектировании морских сооружений. Средний период колебаний по минимумам Тz определяется как продолжительность промежутка времени между минимумами, пересекающими линию среднего положения уровня поверхности на волнограмме. На рис. 12.8 Тz=τ/3. Средний период колебаний по гребням Тс определяется продолжительностью временного периода τ волнограммы, деленной на число гребней. На рис. 12.8 Тc =τ/10; на практике N очень велико, так что погрешность в определении Тс мала. Параметр уширения спектра ε, характеризующий число составляющих колебаний в волне, можно найти из соотношения:

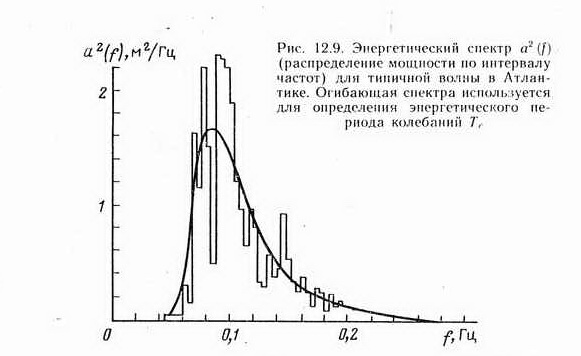
В случае монохроматической волны Тс=Тz, так что ε = 0. В рассматриваемом примере ε = [ 1 — (0,3)2]1/2 = 0,9, что указывает на смешение нескольких частот. Полные данные о вкладе отдельных составляющих волнового движения дает Фурье-анализ энергетического спектра волнения (см., например, рис. 12.9).
Согласно (12.41) мощность на единицу ширины волнового фронта в чисто синусоидальной волне на глубокой воде 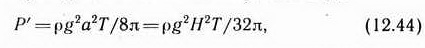
где Н = 2а. Так как среднеквадратическое смещение для чисто синусоидальной волны 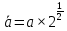 , то (12.44) можно преобразовать к виду (заменив a на , то (12.44) можно преобразовать к виду (заменив a на 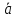 ): ): 
На практике морские волны не являются синусоидальными и монохроматическими. Поэтому мощность на единицу ширины волнового фронта необходимо находить через характерную высоту волн Нs определяемую из (12.42), подставляя ее в (12.45):

Здесь фигурирует так называемый энергетический период Тс, определяемый как период наиболее представительной моды колебаний в энергетическом спектре волны (см. рис. 12.9). Для многих морей:

До последних исследований в волновой энергетике Р' примерно можно определить по данным волнографа следующим образом:
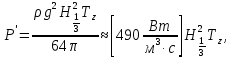 (12.48) (12.48)
однако использование новейшего оборудовании и анализ данных на ЭВМ позволяют получать надежные значения 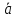 и, следовательно, Hs , а также Тс и Тz , и рассчитать: и, следовательно, Hs , а также Тс и Тz , и рассчитать:
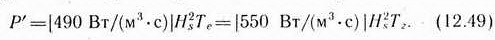
Так как результирующее волнение чаще всего нельзя представить суммой волн, действующих в одном направлении, то мощность, извлекаемая преобразователями направленного действия, будет значительно ниже той, которую переносят волны.
Данные о волнении регистрируются и детально обрабатываются морскими метеостанциями. Вероятно, наиболее важным документом об их деятельности являются диаграммы распределения числа наблюдений волн для заданного района моря за год, составленные в координатах характерная высота — период по впадинам (рис. 12.10). Зная, что период связан с длиной волны (12.9), можно нанести на такую диаграмму и линии равных отношений высоты волн к их длине (градиенты волн).
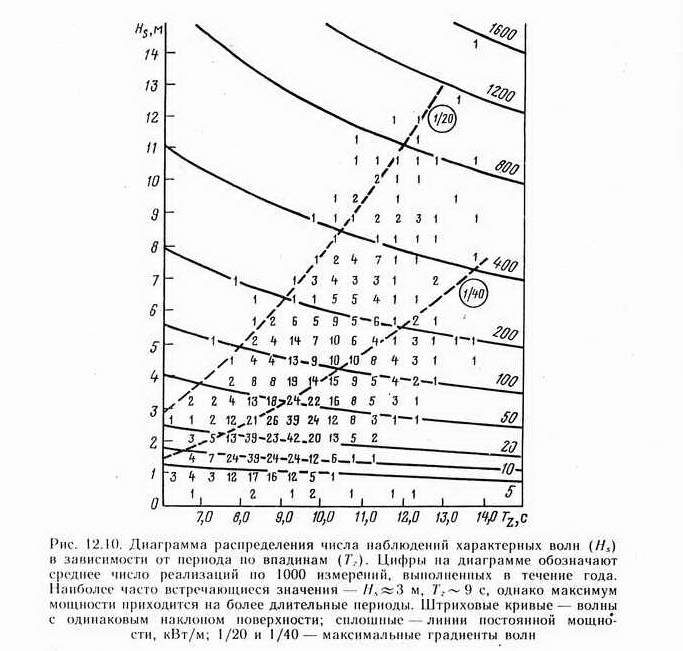
Здесь же обозначаются контуры равных величин за год.
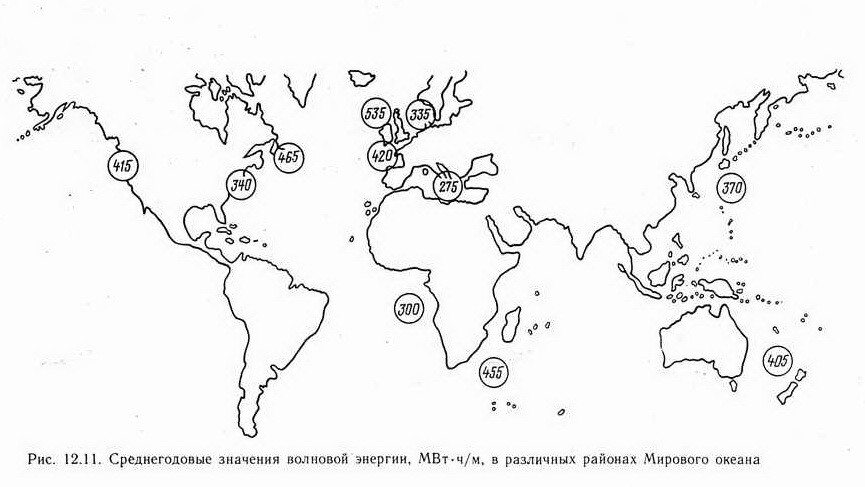
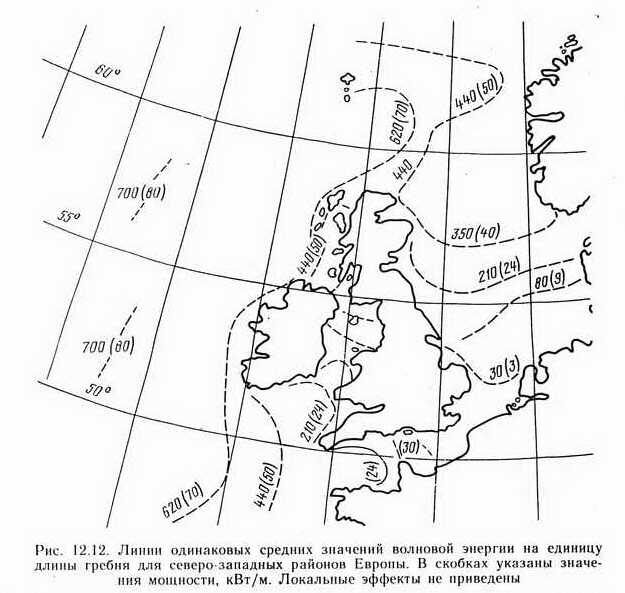
По этим данным можно рассчитать максимальные, средние, минимальные и другие величины мощностей и энергий, связанных с волновыми процессами. Соответствующие цифры можно занести на карты, например, для средних значений за год, как это сделано для планеты в целом и для северо-западной части морей, омывающих Европу (рис. 12.11 и 12.12).
12.5. Устройства для преобразования энергии волн
В результате волнового движения жидкости в волне одновременно с изменением положения уровня и наклона поверхности происходит изменение кинетической и потенциальной энергии, изменение давления под волной. На основе использования одного характерного признака волнового движения или их комбинации уже создано большое число различных устройств, поглощающих и преобразующих волновую энергию. Сюда же входят и устройства, улавливающие воду с гребней волн и возвращающие ее на средний уровень или к подножию волн после преобразования потенциальной энергии. Кроме того, можно использовать самые разнообразные сооружения для увеличения интенсивности волнового движения в местах размещения преобразователей за счет дифракционных и канальных эффектов.
Устройства, отслеживающие профиль волны. Стефан Солтер из Эдинбургского университета разработал устройство, которое назвал «уткой». Форма ее обеспечивала максимальное извлечение мощности (рис. 12.13).
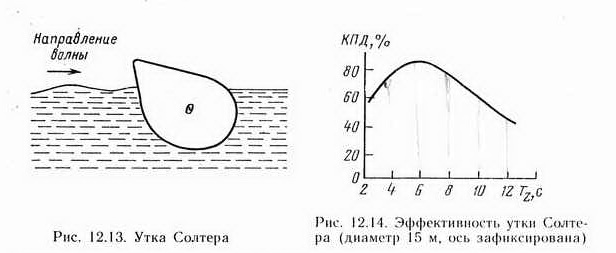
Волны, поступающие слева, заставляют утку колебаться. Цилиндрическая форма противоположной поверхности обеспечивает отсутствие распространения волны направо при колебаниях утки вокруг оси О. Мощность может быть снята с оси колебательной системы с таким расчетом, чтобы обеспечить минимум отражения энергии. Отражая и пропуская лишь незначительную часть энергии волн (примерно 5%), это устройство обладает весьма высокой эффективностью преобразования в широком диапазоне частот возбуждающих колебаний (рис. 12.14).
Дальнейшие разработки Солтера направлены на то, чтобы обеспечить утке способность противостоять ударам максимальных волн и создать заякоренную гирлянду преобразователей в виде достаточно гибкой линии. Предполагается, что характерный размер реальной утки будет равен примерно 0,1λ, что для 100-метровых атлантических волн соответствует 10 м. Нить из уток протяженностью несколько километров предполагается установить в районе с наиболее интенсивным волнением западнее Гебридских островов, мощность всей станции будет примерно 100 МВт. Проектируются и индивидуальные утки, устанавливаемые в заякоренных плотах и предназначаемые для работы на меньших глубинах (примерно 20 м).
Любые волновые преобразователи имеют какие-то недостатки, но для уток наиболее серьезными оказываются следующие:
1) необходимость передачи медленного колебательного движения на привод генератора (Солтер работает над применением в качестве генераторов встроенных гироскопов, которые должны выдавать в сеть мощность, пропорциональную медленному вращению корпусов уток на волнении);
2) необходимость снятия мощности с плавающего на значительной глубине устройства большой протяженности.
Другой характерный тип устройства данного класса — ланкастерский «моллюск», использующий тот же «геометрический» принцип Солтера. Здесь клювообразный поплавок соединен с несколькими податливыми воздушными оболочками, заполненными воздухом, сжимаемым под действием волн. Сжатый воздух перегоняется из одной оболочки в другую по мере того, как волна поворачивает «клюв». Осциллирующий воздушный поток приводит в действие турбину Уэлса, отличающуюся тем, что направление ее вращения не зависит от направления потока воздуха. Турбина связана с электрогенератором.
Колеблющийся водяной столб. При набегании волны на частично погруженную полость, открытую под водой, столб жидкости в полости колеблется, вызывая изменения давления в газе над жидкостью. Полость может быть связана с атмосферой через турбину. Поток может регулироваться так, чтобы проходить через турбину в одном направлении, или может быть использована турбина Уэлса. Уже известны по крайней мере два примера коммерческого использования устройств на этом принципе— сигнальные буи, внедренные в Японии Масудой и в Великобритании сотрудниками Королевского университета Белфаста. Более крупное и впервые включенное в энергосеть устройство построено в Тофтестоллене (Норвегия) фирмой Kvaernor Вrug A/S (рис. 12.15).
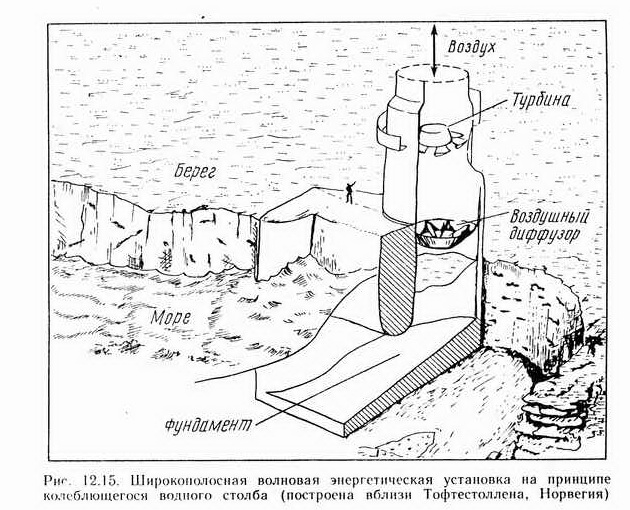
Основной принцип действия колеблющегося столба показан на рис. 12.16.
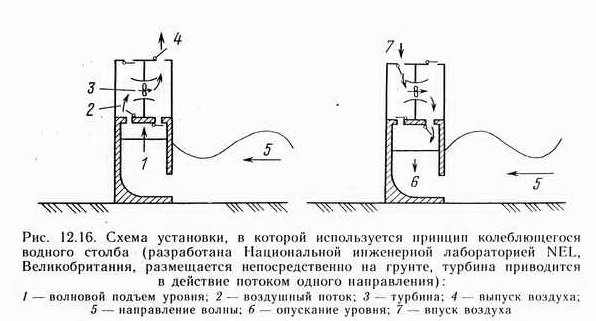
В Тофтестоллене он используется в 500-киловаттной установке, построенной на краю отвесной скалы. Кроме того, национальная электрическая лаборатория (NEL) Великобритании предлагает конструкцию, устанавливаемую непосредственно на морском дне.
Главное преимущество устройств на принципе водяного колеблющегося столба состоит в том, что скорость воздуха перед турбиной может быть значительно увеличена за счет уменьшения проходного сечения канала. Это позволяет сочетать медленное волновое движение с высокочастотным вращением турбины. Кроме того, здесь создается возможность удалить генерирующее устройство из зоны непосредственного воздействия соленой морской воды.
Подводные устройства. Преимущества подводных устройств состоят в том, что эти устройства позволяют избежать штормового воздействия на преобразователи. Однако при их использовании увеличиваются трудности, связанные с извлечением энергии и обслуживанием. Для примера можно предложить так называемый «бристольский цилиндр», представляющий собой наполненный воздухом плавучий корпус, закрепленный под водой на опорах, установленных на грунте. Цилиндр находится под воздействием подповерхностного движения вод и изменения гидростатического давления. Вмонтированные в опоры гидравлические насосы преобразуют энергию движения цилиндра. Перекачиваемая ими жидкость может подаваться на генераторную станцию, единую для нескольких цилиндров, по трубопроводам.
Системы, улавливающие волны. Схемы подобных устройств используют явление, часто наблюдаемое в природных лагунах. Волна разбивается на откосе дамбы (вариант естественного рифа), и вода забрасывается на высоту, превышающую средний уровень моря, заполняя бассейн. Вода может быть возвращена обратно в море через низконапорную турбину. На рис. 12.17 приведена схема, детально прорабатываемая для условий острова Маврикий и предназначенная для обеспечения генерирования 20 МВт электрической мощности.
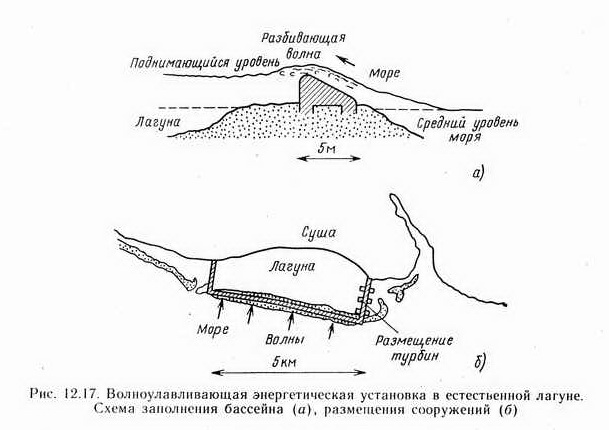
При удельной величине мощности волн 22 кВт/м эффективность такого устройства будет не ниже 30% (имеется в виду преобразование кинетической энергии воли в потенциальную энергию жидкости в бассейне). Необходимая длина морской дамбы равна примерно 5 км. Первая в мире коммерческая станция на этом принципе построена в Норвегии в районе с естественной фокусировкой волн. |
|
|
 Скачать 1.13 Mb.
Скачать 1.13 Mb.







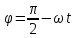 , (12.1)
, (12.1)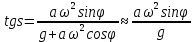 , (12.2)
, (12.2)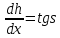 , (12.3)
, (12.3)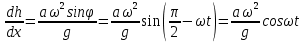 , (12.4)
, (12.4)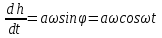 , (12.5)
, (12.5)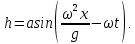 (12.6)
(12.6)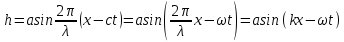 , (12.7)
, (12.7)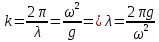 , (12.8)
, (12.8)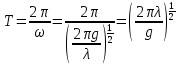 , (12.9)
, (12.9)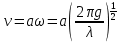 , (12.10)
, (12.10)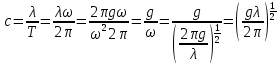 , (12.11)
, (12.11)
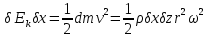 , (12.16)
, (12.16)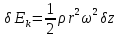 . (12.17)
. (12.17)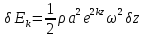 , (12.18)
, (12.18)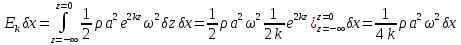 , (12.19)
, (12.19)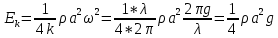 , (12.20)
, (12.20)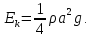 (12.21)
(12.21)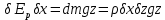 ;
;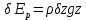 ;
;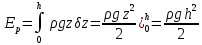 ;
;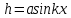 - уравнение движения волновой поверхности, без учета изменения ее формы во времени;
- уравнение движения волновой поверхности, без учета изменения ее формы во времени;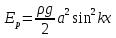 ,
,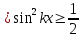 - среднее значение функции;
- среднее значение функции;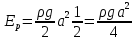 ;
;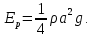 (12.22)
(12.22)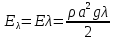 , (12.25)
, (12.25)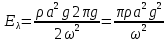 , (12.26)
, (12.26)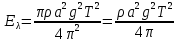 . (12.27)
. (12.27) 
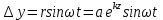 . (12.29)
. (12.29)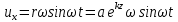 . (12.30)
. (12.30) 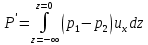 , (12.31)
, (12.31)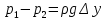 . (12.32)
. (12.32)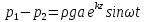 . (12.33)
. (12.33) . (12.34)
. (12.34)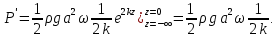 (12.35)
(12.35)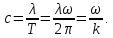 (12.36)
(12.36)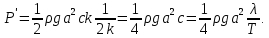 (12.37)
(12.37)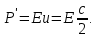 (12.38)
(12.38)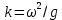 , (12.39)
, (12.39) 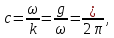 (12.40)
(12.40) 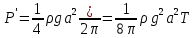 , (12.41)
, (12.41)

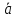 — корень квадратный из среднего квадрата перемещения волной поверхности от положения среднего уровня поверхности, рассчитанный по n измерениям, выполненным за одинаковые интервалы времени, позволяет избежать погрешностей измерения за счет записи волнового процесса на частоте, в 2 раза меньшей, чем максимальная. Измеренная или наиболее вероятная максимальная высота волн Нmax 1 раз в 50 лет может принять значение, равное 50Нs. Именно это значение закладывается в расчеты при проектировании морских сооружений. Средний период колебаний по минимумам Тz определяется как продолжительность промежутка времени между минимумами, пересекающими линию среднего положения уровня поверхности на волнограмме. На рис. 12.8 Тz=τ/3. Средний период колебаний по гребням Тс определяется продолжительностью временного периода τ волнограммы, деленной на число гребней. На рис. 12.8 Тc =τ/10; на практике N очень велико, так что погрешность в определении Тс мала. Параметр уширения спектра ε, характеризующий число составляющих колебаний в волне, можно найти из соотношения:
— корень квадратный из среднего квадрата перемещения волной поверхности от положения среднего уровня поверхности, рассчитанный по n измерениям, выполненным за одинаковые интервалы времени, позволяет избежать погрешностей измерения за счет записи волнового процесса на частоте, в 2 раза меньшей, чем максимальная. Измеренная или наиболее вероятная максимальная высота волн Нmax 1 раз в 50 лет может принять значение, равное 50Нs. Именно это значение закладывается в расчеты при проектировании морских сооружений. Средний период колебаний по минимумам Тz определяется как продолжительность промежутка времени между минимумами, пересекающими линию среднего положения уровня поверхности на волнограмме. На рис. 12.8 Тz=τ/3. Средний период колебаний по гребням Тс определяется продолжительностью временного периода τ волнограммы, деленной на число гребней. На рис. 12.8 Тc =τ/10; на практике N очень велико, так что погрешность в определении Тс мала. Параметр уширения спектра ε, характеризующий число составляющих колебаний в волне, можно найти из соотношения:
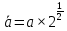 , то (12.44) можно преобразовать к виду (заменив a на
, то (12.44) можно преобразовать к виду (заменив a на 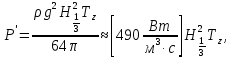 (12.48)
(12.48)





