1 и 2 начало термодинамики. Энергия. Закон сохранения полной механической энергии
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
|
Министерство сельского хозяйства Чеченской республики государственное бюджетное профессиональное образовательное учреждение «Чеченский аграрно-технический колледж» Реферат на тему: «Энергия. Закон сохранения полной механической энергии» Исполнитель: Айдаев Хаважди студент очного отделения ОЭРСТ 21.11 Руководитель: Хаджимуратов Р.Р. г. Грозный 2021г. Содержание Введение…………………………………………………………………..……...3 1. Энергия...……………………………………………………………………….4 2. Кинетическая энергия. …………………………………………….………..10 3. Закон сохранения энергии…………………………………………………..12 Заключение……………………………………………………………………...15 Список литературы……………………………………………………………..16 Введение Законы сохранения занимают среди всех законов природы особое место. Общность и универсальность законов сохранения определяют их большое научное, методологическое и философское значение. Они являются основой важнейших расчетов в физике и ее технических приложениях, позволяют в ряде случаев предсказывать эффекты и явления при исследовании разнообразных физико-химических систем и процессов. С законами сохранения связано введение в современную физику идей, имеющих принципиальное значение. Актуальность работы состоит в том, что законы сохранения энергии при изучении физики играют большую роль в формировании научного мировоззрения учащихся и в практическом применении в науке и технике. Энергия Простые машины обладают способностью совершать работу, но не могут сохранять эту способность, так как одновременно с тем, как они ее получают на одном конце, отдают ее на другом. Однако есть случаи, когда тела могут накапливать способность совершать работу. Существуют специальные механизмы, способные запасти работу, а затем отдать ее. Типичным примером является гиревой завод настенных часов (рис. 1) [1]. 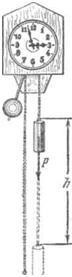 Рисунок 1 – Поднятая гиря обладает запасом работы, который постепенно расходуется на поддержание хода часов Подтягивая гирю вверх, мы совершаем некоторую работу. В результате, которой часовой механизм получает способность совершать в течение длительного времени работу, необходимую для хода часов. То есть работу, с помощью которой будет осуществленная поддержка движения всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов гиря постепенно опускается и запас работоспособности механизма уменьшается. Через некоторое время понадобится снова завести часы, то есть вновь сделать их способными к совершению работы, требующейся для их хода. При заводе часов гиревой механизм накапливает способность производить работу; по мере хода часов способность производить работу расходуется. Поднимая груз, мы запасаем работу; опускаясь, груз способен производить работу. В теле можно накапливать работу не только путем поднятия тела на некоторую высоту, а так же деформируя тело, например, сжимая или растягивая пружину, мы производим работу; в результате деформированное тело получает способность совершать работу. Задавая скорость какому-либо телу, также приходится затрачивать работу, в результате которой тело имеет способность совершать работу, уменьшая свою скорость. Например, при составлении поездов маневровый тепловоз толкает вагон к составу и, останавливаясь, вагон сжимает пружины буферов; пуля, попадающая в препятствие, производит работу, разрушая материал, и т. д. Во всех представленных случаях работа производится при изменении состояния тела: при опускании груза, при раскручивании пружины, при остановке движущегося тела. Пока эти изменения не произошли, работа не произведена. Так же в теле имеется некоторый запас еще не совершенной работы. А при совершении работы этот запас расходуется. Производя же работу над телом: поднимая его вверх, деформируя его, сообщая ему скорость, - мы сообщаем ему запас работы, который в дальнейшем можно использовать, возвращая тело в исходное состояние. Энергией называют запас работы, которую может совершить тело, изменяя свое состояние. В механике существуют разные виды энергии: энергия, связанная с поднятием тела над землей (и вообще энергия, связанная с силами всемирного тяготения); энергия, связанная с деформациями тела; энергия, связанная с движением тел. Изменение энергии определяется той работой, которую надо совершить, чтобы вызвать это изменение. Следовательно, энергию измеряют в тех же единицах, в которых измеряют работу, то есть в джоулях [2]. Потенциальная энергия. Найдем, чему равна работа А, совершаемая некоторой силой F при подъеме тела весом m на высоту h. Будем считать, что движение тела происходит медленно и что силами трения можно пренебречь. Работа против силы тяжести не зависит от того, как мы поднимаем тело: по вертикали (как гирю в часах), по наклонной плоскости (как при поднятии санок в гору) или еще каким-либо способом. Во всех случаях работа А = mgh. При опускании тела на первоначальный уровень сила тяжести произведет такую же работу, какая была затрачена силой F на подъем тела. Значит, поднимая тело, мы запасли работу, равную mgh, т. е. поднятое тело обладает энергией, равной произведению силы тяжести, действующей на это тело, и высоты, на которую оно поднято. Эта энергия не зависит от того, по какому пути происходил подъем, а определяется лишь положением тела (высотой, на которую оно поднято) и называется потенциальной энергией. Итак, потенциальная энергия Ептела, поднятого на некоторую высоту, выражается формулой 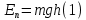 При исходном положении тела работа, которую может совершить тело, то есть его потенциальная энергия, зависит от того, насколько тело может опуститься. В гиревом механизме часов это определяется длиной цепочки, на которой висит гиря, в примере с наклонной плоскостью – высотой наивысшей точки наклонной плоскости над ее минимальной точкой. В других случаях минимальный уровень не может быть так определен. Например, если тело лежит на столе, то можно определять его потенциальную энергию той работой, которую оно совершило бы, опускаясь до пола. Поэтому нужно условиться заранее, от какого уровня отсчитывать высоту, а вместе с тем и значение потенциальной энергии тела. Выбрать этот уровень можно совершенно произвольно, так как во всех физических явлениях всегда важна не сама потенциальная энергия, а ее изменение, которым определяется совершаемая работа. Изменение же потенциальной энергии будет, очевидно, в не зависимости от того какой исходный уровень выбран. Если условия не оговорены, мы будем считать потенциальную энергию тела, лежащего на поверхности земли, равной нулю. Тогда в формуле (1) в качестве h следует брать высоту поднятия тела над поверхностью земли. Если тело имеет значительные размеры, то под h в формуле (6) нужно понимать расстояние от поверхности земли (или от иного нулевого уровня) до центра тяжести тела [1]. 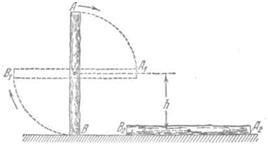 Рисунок 2 - При переходе столба из положения АВ в положениеА1В1сила тяжести не совершает работы, так как центр тяжести тела остается на месте. При переходе из положения А1В1 в положение A2В2 совершается работаmgh. Например, определим насколько потенциальная энергия вертикально стоящего столба рис. 4 в положение АВ, больше потенциальной энергии того же столба, лежащего на земле (положение A2В2). Представим себе, что столб переходит из положения АВ в положение A2B2в два приема. Сначала он поворачивается вокруг центра тяжести (в данном случае около средней точки) в положение A1B1. При этом верхняя часть столба опускается, а нижняя поднимается; и сила тяжести совершает над верхней частью столба положительную работу, а над нижней — равную ей отрицательную работу, и полная работа силы тяжести равна нулю. Только при переходе из положения А1В1в положение А2В2сила тяжести совершает положительную работу. Следовательно, потенциальная энергия стоящего на земле столба больше потенциальной энергии столба, лежащего на земле, на величину mgh, где m — масса столба и h — разность высот центра тяжести в положениях АВ и A2В2. При подсчете потенциальной энергии жидкости массы m, находящейся в цилиндрическом сосуде (рис. 3), следует взять высоту H центра тяжести жидкости С над нулевым уровнем, т. е. высоту h0дна сосуда над нулевым уровнем, плюс половину высоты уровня жидкости в сосуде h1/2, так что потенциальная энергия будет равна: 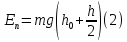 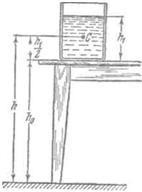 Рисунок 3 - К расчету потенциальной энергий жидкости в сосуде Потенциальная энергия упругой деформации. Деформированное упругое тело (например, растянутая или сжатая пружина) способно, возвращаясь в исходное состояние, совершив работу над соприкасающимися с ним телами. Следовательно, упругое деформированное тело обладает потенциальной энергией. Она зависит от взаимного положения частей тела, например, витков пружины. Работа, которую может совершить растянутая пружина, зависит от начального и конечного растяжения пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к первоначальному состоянию, таким образом, найдем потенциальную энергию растянутой пружины. Пусть растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. Нужно учитывать, что сила, с которой действует пружина, не остается постоянной, а изменяется пропорционально растяжению. Если первоначальное растяжение пружины, считая от нерастянутого состояния, равнялось l, то первоначальное значение силы упругости составляло F=kl, где k — коэффициент пропорциональности, который называют жесткостью пружины. По мере сокращения пружины эта сила линейно убывает от значения kl до нуля. Значит, среднее значение силы равно Fср=kl/2. Можно показать, что работа А равна этому среднему, умноженному на перемещение точки приложения силы: 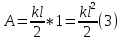 Таким образом, потенциальная энергия растянутой пружины 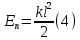 Такое же выражение получается для сжатой пружины. В формуле (4) потенциальная энергия выражена через жесткость пружины и через ее растяжение l. Заменив l на F/k, где F – упругая сила, соответствующая растяжению (или сжатию) пружины l, получим выражение: 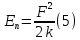 которое определяет потенциальную энергию пружины, растянутой (или сжатой) силой F. Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, тем меньше ее потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной растягивающей силе. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на перемещение точки приложения силы, т. е. работа. Данная закономерность имеет большое значение, например, при устройстве различных рессор и амортизаторов: при посадке на землю самолета амортизатор шасси, сжимаясь, должен произвести большую работу, гася вертикальную скорость самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато возникающие силы упругости будут меньше и самолет будет лучше предохранен от повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки ощущаются резче, чем при слабой накачке [3]. 2. Кинетическая энергия. Тела могут обладать некоторым запасом работы, то есть обладать энергией, не только при определенном положение в пространстве или деформирование, но и если тело обладает скоростью. Так, вагон может въехать на гору, если он вначале обладает некоторой скоростью; пуля или снаряд могут подняться на значительную высоту, если они вылетают из дула с большой скоростью. В этих случаях движущееся тело, поднимаясь вверх, совершает работу против силы тяжести. Так же движущееся тело совершает работу против сил упругости. Например, бумажный шарик, привязанный к тонкой резиновой нити, может сильно растянуть эту нить, если шарику сообщить толчком большую скорость (рис. 4). Когда один катящийся вагон ударяется своими буферами о буфера другого вагона, то пружины буферов сильно сжимаются, т. е. совершается работа сжатия пружины.  Рисунок 4 - Быстро летящий бумажный шарик растягивает резиновую нить Во всех перечисленных примерах тело совершает работу потому, что оно обладает определенной скоростью. Покоящийся вагон не может въехать на гору, не может сжать буферных пружин. Всякий раз, когда тело совершает работу благодаря тому, что оно движется и под воздействием сил сопротивления, скорость его движения будет уменьшаться. Если скорость тела уменьшится до нуля, то запас способности совершать работу за счет движения тела будет исчерпан. Значит, всякое движущееся тело обладает некоторым определенным запасом способности совершать работу, то есть определенной энергией. Энергией движущегося тела называют кинетической энергией. Механическая энергия образуется при сложении кинетической и потенциальной энергии [4]. Выражение кинетической энергии через массу и скорость тела. Выше рассмотрено, что можно создать запас потенциальной энергии, заставляя какую-либо силу совершать работу: поднимая груз или сжимая пружину. Точно так же можно создать и запас кинетической энергии в результате работы какой- либо силы. Действительно, если тело под действием внешней силы получает ускорение и перемещается, то эта сила совершает работу, а тело приобретает скорость, т. е. приобретает кинетическую энергию. Например, сила давления пороховых газов в стволе ружья, выталкивая пулю, совершает работу, за счет которой и создается запас кинетической энергии пули. Обратно, если вследствие движения пули совершается работа (например, пуля поднимается вверх или, попадая в препятствие, производит разрушения), то кинетическая энергия пули уменьшается. Переход работы в кинетическую энергию можно проследить на примере когда на тело действует только одна сила (в случае многих сил это — равнодействующая всех сил, действующих на тело). Предположим, что на тело массы m, находившееся в покое, начала действовать постоянная сила F; под  действием силы Fтело будет двигаться равноускоренно с ускорением действием силы Fтело будет двигаться равноускоренно с ускорением 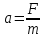 . Пройдя расстояние sв направлении действия силы, тело приобретет скорость . Пройдя расстояние sв направлении действия силы, тело приобретет скорость  υ, связанную с пройденным расстоянием формулой υ, связанную с пройденным расстоянием формулой 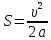 . Отсюда находим работу Асилы F: . Отсюда находим работу Асилы F: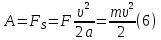 Точно так же, если на тело, движущееся со скоростью υ, начнет действовать сила, обратная направлению скорости движения, то оно будет замедлять свое движение и остановится, произведя до остановки работу против  действующее силы, также равную действующее силы, также равную 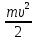 . Значит, кинетическая энергия Eкдвижущегося тела равна половине произведения его массы на квадрат скорости: . Значит, кинетическая энергия Eкдвижущегося тела равна половине произведения его массы на квадрат скорости: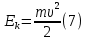 Поскольку изменение кинетической энергии, так же как и изменение потенциальной энергии, равно работе (положительной или отрицательной), произведенной при этом изменении, то кинетическая энергия также измеряется в джоулях. Закон сохранения энергии. Если на тело действует сжатая пружина, то она может придать телу некоторую скорость, т. е. кинетическую энергию, но при этом пружина будет распрямляться, и ее потенциальная энергия будет уменьшаться; сумма потенциальной и кинетической энергий останется постоянной. Если на тело, кроме пружины, действует еще и сила тяжести, то хотя при движении тела энергия каждого вида будет изменяться, но сумма потенциальной энергии тяготения, потенциальной энергии пружины и кинетической энергии тела оставаться неизменной. Энергия может переходить из одного вида в другой, может переходить от одного тела к другому, но общий запас механической энергии остается неизменным. Опыты и теоретические расчеты показывают, что при отсутствии сил трения и при воздействии только сил упругости и тяготения суммарная потенциальная и кинетическая энергия тела или системы тел остается во всех случаях постоянной. В этом и заключается закон сохранения механической энергии. 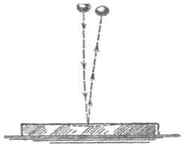 Рисунок 5 - Отразившись от стальной плиты, стальной шарик подскакивает снова почти на ту же высоту, с которой он был брошен Проиллюстрируем закон сохранения энергии на следующем опыте. Стальной шарик, упавший с некоторой высоты на стальную или стеклянную плиту и ударившийся об нее, подскакивает почти на ту же высоту, с которой упал (рис. 5). Во время движения шарика происходит целый ряд превращений энергии. При падении потенциальная энергия переходит в кинетическую энергию шарика. Когда при прикосновении шарика к плите, и шарик и плита подвергаются деформации. Кинетическая энергия превращается в потенциальную энергию упругой деформации шарика и плиты, причем этот процесс продолжается до тех пор, пока шарик не остановится, до тех пор, пока вся его кинетическая энергия не перейдет в потенциальную энергию упругой деформации. Затем под действием сил упругости деформированной плиты шарик приобретает скорость, направленную вверх: энергия упругой деформации плиты и шарика превращается в кинетическую энергию шарика. При дальнейшем движении вверх скорость шарика под действием силы тяжести уменьшается, и кинетическая энергия превращается в потенциальную энергию тяготения. В наивысшей точке шарик обладает снова только потенциальной энергией тяготения. Поскольку можно считать, что шарик поднялся на ту же высоту, с которой он начал падать, потенциальная энергия шарика в начале и в конце описанного процесса одна и та же. Более того, в любой момент времени, при всех превращениях энергии сумма потенциальной энергии тяготения, потенциальной энергии упругой деформации и кинетической энергии все время остается неизменной, т. е. закон сохранения механической энергии выполнен. Теперь, мы можем объяснить: почему нарушался закон сохранения работы в простой машине, которая деформировалась при передаче работы. Дело в том, что работа, затраченная на одном конце машины, частично или полностью затрачивалась на деформацию самой простой машины (рычага, веревки и т. д.), создавая в ней некоторую потенциальную энергию деформации, и лишь остаток работы передавался на другой конец машины. В сумме переданная работа вместе с энергией деформации оказывается равной ранее затраченной работе. В случае абсолютной жесткости рычага простая машина не может накопить в себе энергию, и вся работа, произведенная на одном ее конце, передается на другой конец [5]. Силы трения и закон сохранения механической энергии. Присматриваясь к движению шарика, подпрыгивающего на плите, можно обнаружить, что после каждого отскока, шарик поднимается на несколько меньшую высоту, чем раньше (рис. 8), т. е. полная энергия не остается в точности постоянной, а понемногу убывает. Это значит, что закон сохранения энергии в таком виде, как мы его сформулировали, соблюдается в этом случае только приближенно. Причина заключается в том, что в этом опыте возникают силы трения: сопротивление воздуха, в котором движется шарик, и внутреннее трение в самом материале шарика и плиты. Вообще, при наличии трения закон сохранения механической энергии всегда нарушается и полная энергия тел уменьшается. За счет этой убыли энергии и совершается работа против сил трения. Заключение Всеобщий характер закона сохранения энергии. Силы трения занимают особое положение в вопросе о законе сохранения механической энергии. Если сил трения нет, то закон сохранения механической энергии соблюдается в том виде, что полная механическая энергия системы остается постоянной. Если же действуют силы трения, то энергия уже не остается постоянной, а уменьшается при движении. Но при этом всегда растет внутренняя энергия. С развитием физики обнаруживались все новые виды внутренней энергии: световая энергия, энергия электромагнитных волн, химическая энергия, проявляющаяся при химических реакциях (в качестве примера достаточно указать хотя бы на химическую энергию, запасенную во взрывчатых веществах и превращающуюся в механическую и тепловую энергию при взрыве); так же была открыта ядерная энергия. Оказалось, что совершаемая над телом работа равна приращению суммы всех видов энергии тела; работа же, совершаемая некоторым телом над другими телами, равна уменьшению суммарной энергии данного тела. Для всех видов энергии оказалось, что переход энергии из одного вида в другой, переход энергии от одного тела к другому, что при всех переходах общая энергия всех видов все время остается постоянной. В этом и заключается всеобщий закон сохранения энергии. Хоть общее количество энергии может оставаться постоянной, но количество полезной энергии может постоянно уменьшаться. Переход энергии в другую форму может означать переход ее в бесполезную для нас форму. В механике чаще всего это — нагревание окружающей среды, трущихся поверхностей и т. п. Такие потери не только невыгодны, но даже вредно отзываются на самих механизмах; так, во избежание перегревания приходится специально охлаждать трущиеся части механизмов [6]. Список литературы Гершензон Е.М., Малов Н.Н. Курс общей физики: Механика. – М.: Просвещение, 2007. – 127 с. Беликов Б.С. Решение задач по физике. Общие методы. – М.: Высшая школа, 2002. – 303 с. Шевцов В.А. Законы сохранения в механике. – М.: Просвещение, 2003. – 263 с. Свитков Л.П. Термодинамика и молекулярная физика. - М.: Просвещение, 2012. – 260 с. Яворский Б.М., Пинский А.А. Основы физики. – М.: Наука, 2002. – 102 с. Кикоин И.К, Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Просвещение, 2004. -191 с. |
