Лекция 1. Введение. Основные понятия статики.. Лекции рассматриваются следующие вопросы Введение. Элементы векторной алгебры

• Название: Лекции рассматриваются следующие вопросы Введение. Элементы векторной алгебры
• Дата: 11.01.2022
• Размер: 299.18 Kb.
• Имя файла: Лекция 1. Введение. Основные понятия статики..docx
• Тип: Лекции; #328283
• страница: 1 из 4

Лекция 1. Введение. Основные понятия статики.

В данной лекции рассматриваются следующие вопросы

1. Введение.

2. Элементы векторной алгебры.

3. Основные понятия статики.

4. Аксиомы статики.

5. Связи и их реакции.

Изучение этих вопросов необходимо в дальнейшем для изучения центра тяжести, произвольной пространственной системы сил, сил трения скольжения, моментов трения качения, решения задач в дисциплине «Сопротивление материалов».

 

 

Введение

Развитие современной техники ставит перед инженерами самые разнообразные задачи, связанные с расчетом различных сооружений (зданий, мостов, каналов, плотин и т. п.), с проектированием, произ­водством и эксплуатацией всевозможных машин, механизмов, двига­телей и, в частности, таких объектов, как автомобили, тепловозы, морские и речные суда, самолеты, ракеты, космические корабли и т. п. Несмотря на многообразие всех этих проблем, решения их в определенной части основываются на некоторых общих принципах и имеют общую научную базу. Объясняется это тем, что в назван­ных задачах значительное место занимают вопросы, требующие изуче­ния законов движения или равновесия тех или иных материальных тел.

Наука об общих законах движения и равновесия материальных тел и о возникающих при этом взаимодействиях между телами на­зываетсятеоретической механикой. Теоретическая механика представляет собой одну из научных основ современных технических дисциплин.

Механикой в широком смысле этого слова называется наука, посвящен­ная решению любых задач, связанных с изучением движения или равновесия тех или иных материальных тел и происходящих при этом взаимодействий между телами. В качестве материальных объектов помимо дискретных тел могут выступать среды – например, жидкость или газ и поля, поэтому круг объектов, изучаемых механикой очень широк.

В зависимости от физических свойств этих объектов и их размеров всю механику можно разделить на классическую или ньютонову и неклассическую.

Неклассическая механика  это действительно часть физики, в которой исследуются объекты микро- и макромира с учетом пространственно-временной зависимости.

Классическая механика имеет дело с объектами, протяженность которых приблизительно и с точностью до нескольких порядков заключена в интервале от 10^-10 до 10¹⁰ метра. При их изучении свойства пространства и времени можно считать постоянными. Именно такуюньютонову механику мы и будем рассматривать в дальнейшем.

В зависимости от особенностей модели реальных объектов классическая механика делится на теоретическую механику  с моделью абсолютно твердого тела и механику сплошной среды с моделью деформируемого тела.

Основным методом исследования в механике является гипотетико-дедуктивный. Его суть заключается в выдвижении гипотезы, которая подтверждается или опровергается опытом.

Схематически место механики в системе естествознания можно определить так, как показано на рисунке ниже. При этом механика деформируемого тела или механика сплошной среды, образующая ядро этой науки, окружена тремя сегментами, представляющими собой теоретическую механику, неклассическую механику микро- и макромира и прикладную механику, которые примыкают соответственно: к математике, физике и практике в широком смысле этого слова.

Под прикладной механикой понимают раздел механики, в котором ее выводы и методы применяют для решения задач проектирования, строительства и эксплуатации сооружений. Этот термин близок к понятиям «техническая» или «строительная» механика.



 

Теоретическая механика представляет собою часть механики, в которой изучаются общие законы движения и взаимодействия материаль­ных тел, т.е. те законы, которые, например, справедливы и для движения Земли вокруг Солнца и для полета ракеты или артиллерийского снаряда и т. п.

Под движением в механике мы понимаем механическое движение, т.е. происходящее с течением времени изменение взаимного положения материальных тел в пространстве.

Механическим взаимо­действием между телами называется тот вид взаимодействия, в резуль­тате которого происходит изменение движения этих тел или изме­нение их формы (деформация). Величина, являющаяся количественной мерой механического взаимодействия тел, называется в механике силой.

Основной задачей теоретической механики является изучение общих законов движения и равновесия материальных тел под действием приложенных к ним сил.

По характеру рассматриваемых задач теоретическую механику принято разделять на статику, кинематику и динамику.

Статикарассматривает частный случай механического движения, когда оно не зависит от времени – речь идет о рассмотрении равновесия твердого тела, загруженного системой сил и находящегося в состоянии покоя.

Кинематикарассматривает внешнюю сторону механического движения независимо от причин, вызвавших его. Это не что иное, как геометрия в четырехмерном пространстве, где время играет роль четвертого измерения.

Если известно положение движущейся точки в каждый момент времени, то кинематика позволяет построить ее траекторию и определить такие кинематические параметры, как скорость или ускорение.

Динамикаисследует общий случай механического движения твердого тела с учетом причин, вызвавших его.

Термин «механика» впервые появляется в сочинениях одного из выдающихся философов древности Аристотеля (384—322 до н. э.) и происходит от греческого слова μηχαυή, означающего по современным понятиям «сооруже­ние», «машина», «изобретение»

В древние времена, когда запросы производства сводились главным образом к удовлетворению нужд строительной техники, начи­нает развиваться учение о так называемых простейших машинах (блок, ворот, рычаг, наклонная плоскость) и общее учение о равно­весии тел (статика). Обоснование начал статики содержится уже в сочинения одного из великих ученых Архимеда (287 – 212 г. но н. э.). 

В России на развитие первых исследований по механике большое влияние оказали труды гениального ученого и мыслителя М. В. Ломо­носова (1711—1765). Из многочисленных отечественных ученых, внесших значительный вклад в развитие различных областей теоретической механики, прежде всего, должны быть названы: М. В. Остроградский (1801—1861), которому принадлежит ряд важных исследований по аналитическим методам решения задач меха­ники; П. Л. Чебышев (1821—1894), создавший новое направление в исследовании движения механизмов; С. В. Ковалевская (1850—1891), решившая одну из труднейших задач динамики твердого тела; И. В. Мещерский (1859—1935), заложивший основы механики тел переменной массы; К. Э. Циолковский (1857—1935), сделавший ряд фундаментальных открытий в теории реактивного движения; А. Н. Крылов (1863—1945), разработавший теорию корабля и много внесший в развитие теории гироскопиче­ских приборов.

Выдающееся значение для развития механики имели труды «отца русской авиации» Н. Е. Жуковского (1847—1921) и его ближайшего ученика С. А. Чаплыгина (1869—1942). Характерной чертой в творчестве Н. Е. Жуковского было приложение методов механики к решению актуальных технических задач. Большое влия­ние идеи Н. Е. Жуковского оказали и на преподавание теоретической механики в высших технических учебных заведениях нашей страны.

Стоящая в наши дни перед отечественной наукой и техникой задача непрерывного роста и внедрения в производство новой техники требует дальнейшего повышения качества подготовки инженерных кадров, расширения теоретической базы их знаний. Известную роль в реше­нии этой задачи должно сыграть и изучение одной из научных основ современной техники – теоретической механики.

 

Элементы векторной алгебры

В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.

1. Понятие вектора.

Для определенности рассматриваем прямоугольную декартову систему координат. 

Вектор- это направленный отрезок, который характеризуется длиной и направлением.

Операции над векторами.  Вектора можно складывать и умножать на число.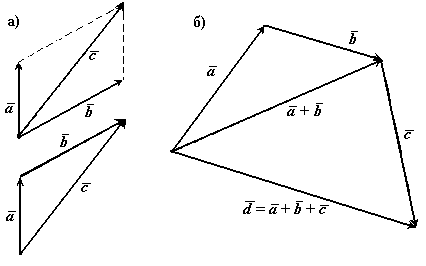

 - сумма двух векторов есть вектор

α∙  - произведение вектора на действительное число есть вектор

 - существует нулевой вектор



Рис.1

 

В математике все вектора являются свободными, их можно переносить параллельно самим себе.

В сумме двух векторов (рис.1,а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис.1,б)  получаем, что суммой  нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.

Операции над векторами подчиняются следующим законам  (см. рис.2):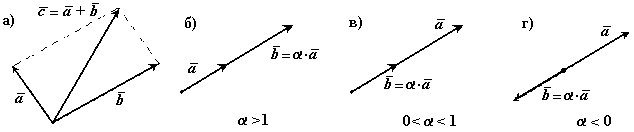







 



Рис.2

 

2. Правые и левые системы координат.

Декартовы системы координат делятся на два вида: правую и левую.

Рассмотрим декартовы системы координат на плоскости (см. рис. 3).

При повороте оси  Ox  правой системы координат на 90^о против часовой стрелки она совпадает с осью Oy .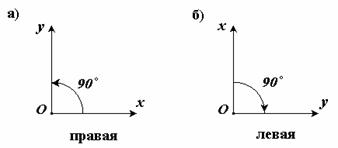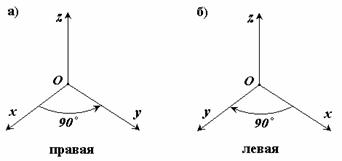



Рис.3                                              Рис.4

 

Рассмотрим декартовы системы координат в пространстве  (см. рис.4).

При повороте оси  Ox  правой системы координат вокруг оси Oz на 90⁰ против часовой стрелки она совпадает с осью Oy .

3. Длина, проекции и направляющие косинусы вектора.

В дальнейшем будем рассматривать правую декартову систему координат. Единичные вектора вдоль осей  Ox,  Oy  и  Oz  образуют систему единичных  (или базисных)  векторов. Любой вектор, имеющий начало в точке  O, можно представить как сумму 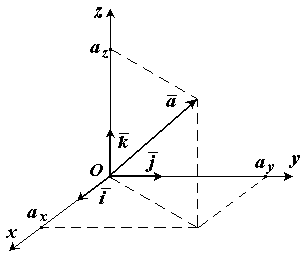 ,  числа  (a_x, a_y, a_z)  -  это проекции вектора   на оси координат  (см. рис.5).



Рис.5

 

Длина (или модуль) вектора   определяется формулой    и обозначается a или  | |.

Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону  (см. рис.6).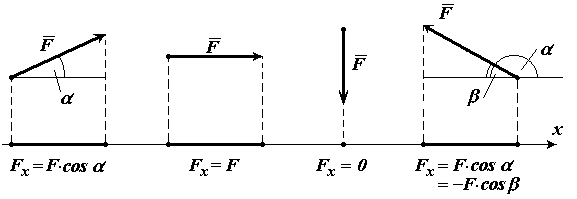



Рис.6

 

Направляющими косинусами    вектора называются косинусы углов между вектором и положительными направлениями осей  Ox,  Oy  и  Oz  соответственно.



Любая точка пространства с координатами  (x, y, z) может быть задана своим радиус-вектором



Координаты  (x, y, z)  это проекции вектора     на оси  координат.

4. Скалярное произведение двух векторов

Имеется два вектора 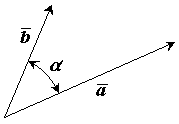   и  .   

,

.



Рис.7

 

Результатом скалярного произведения двух векторов    и   является  скалярная величина (число).

Записывается как   или  ( ,  ).  Скалярное произведение двух векторов равно   

Свойства скалярного произведения:











5. Векторное произведение двух векторов

Имеется два вектора   .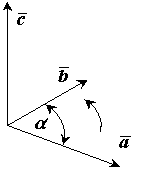

  

.



Рис.8

 

Результатом векторного произведения двух векторов    является  вектор  .  Записывается как     или  [ .].

Векторное произведение двух векторов это вектор , перпендикулярный к обоим этим векторам, и направленный так, чтобы  с его конца  поворот вектора     к вектору    был виден против часовой стрелки.

Длина  (или модуль)  векторного произведения равна  | .

Свойства векторного произведения:







 

Векторное произведение двух векторов вычисляется через их проекции следующим образом: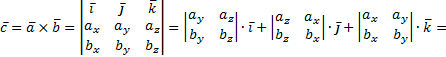











 

Основные понятия статики

                Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.

Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не де­формируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.

Исследованием движения нетвердых тел – упругих, пластичных, жидких, газообразных, занимаются другие науки (сопротивление мате­риалов, теория упругости, гидродинамика и т.д.).

Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.

Основные понятия:

1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.

В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН).

Сила является величиной векторной.

Ее действие на тело опре­деляется: 1) численной величиной или модулем силы, 2) направле­нием силы, 3) точкой приложения силы (рис.9).

Например, будем прикладывать к стулу одну и ту же по модулю силу F. При приложении силы сверху вниз стул остается в состоянии покоя; при положении силы снизу вверх - стул поднимается; изменим направление нагружения, приложим силу горизонтально к спинке стула - стул опрокинется. Так как во всех случаях направление и место приложения силы различны, то и результат действия силы на стул разный, несмотря на то, что модуль силы F во всех случаях одинаков.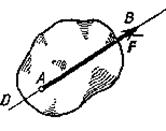